集对论在人工智能中的若干应用与进展综述

赵克勤

(诸暨市联系数学研究所 诸暨 311800)

1 引言

集对论(Set Pair Theory, SPT)是集对分析理论(Set Pair Analysis Theory, SPAT)的简称，基本概念是集对(Set Pair, SP),主要数学工具是联系数(Connection Number, CN)[1–5]；自笔者1989年提出以来，已在包括人工智能在内的系统与信息科学等众多领域得到应用，在中国知网，用“篇关摘”、“集对分析”、“集对论”、“联系数”，可以检索到《集对分析在人工智能中的应用与进展》等中英文文献4 000多篇，其中博硕士学位论文1 000多篇[6,7]，内容涉及航空航天、多雷达信号分选、军事国防、暴雨预报、水文水资源、地质矿山、生态环境、社会经济、能源交通、物流运输、网络通讯、机电制造、农业育种、工程施工、中医药与卫生统计、计算机与人工智能、系统预测与管理决策、安全与非传统安全、教学与体育等，论文发表趋势见图1(中国知网)；用“篇关摘”集对分析+智能，检到文献136篇，论文发表趋势见图2(中国知网)；出版《人工智能集对分析》等专著10余部[8]；究其原因，是集对论把事物所在的时空视为一个既确定又不确定(Deterministic Uncertainty, D-U)时空，把事物的确定性与不确定性作为一个确定不确定系统处理，对不确定性“客观承认、系统描述、定量刻画、具体分析、实践检验”，把人们对事物的确定性信息与不确定性信息相互关系的辩证认识转换成具体的数学工具—联系数，借助联系数的建模计算与不确定性的系统分析，处理各种不确定性问题。

图1 1994年以来研用集对分析的论文发表趋势

图2 1995年以来把集对分析用于人工智能方面的论文发表趋势

为促进集对论在新一代人工智能中有更多更好应用和集对论自身的发展完善，本文拟在文献[1–8]的基础上，先概述集对及其联系数的来源，集对论的成对原理与不确定原理、不确定性系统理论与同异反系统理论、以及联系数的基本算法；再概述集对论在智能来源与智能定义、航天数据快速评估和多雷达信号分选以及图像识别、天气降水预报等复杂系统智能预测、不确定性智能决策、群体智能测算、自然数的联系数化、智能制造等人工智能基础创新方面的若干应用；最后就集对论在绿色智能算法方面的若干进展作了展望，包括偏联系数计算、联系数的系统能守恒计算、共轭计算、隐形计算，以及“集对论+非集对论”的广义集对论；供人工智能和信息处理等领域的专家学者参考和批评指正。

2 集对论简介

2.1 集对及其联系数的来源与性质

集对和集对的特征函数联系数是集对论的2个基本概念，最早源自上世纪60年代作者学习恩格思《自然辩证法》和数学《集合论》时，对集合论中罗素悖论(Bertrand Russell paradox)的思考[9]。

罗素(Bertrand Russell, 1872～1970年)是英国数学家、逻辑学家与哲学家，于1903年构造了一个集合X，X中的元素X1,X2,···,Xn都不属于自己，然后罗素问：集合X是属于X？还是不属于X？如果回答X不属于X，那么，X属于X；如果回答X属于X，那么X又不属于X，无论如何都自相矛盾。

为了说明上面这个悖论，罗素于1918年举了个例子：村上有一个理发师贴出公告，宣称他为所有不为自己理发的人理发。现在问：理发师自己的头发该由谁理？如果他不给自己理发，那么按照理发师公告，他应该为自己理发；如果他为自己理发，同样根据理发师公告，理发师不能为自己理发；无论如何，都不能确定该理发师自己由谁理发。

罗素悖论震撼了当时的数学界，著名法国数学家庞加莱(Jules Henri Poincaré, 1854～1912年)坦言：“我们围住了一群羊，而羊群中已混进了狼”。

罗素悖论之所以引起世界数学界的震动，是因为罗素悖论表明：即使构造一个普通的集合，例如把“所有不为自己理发的人组成一个集合A”这样一件普通和简单的事，也遇到令人棘手的不确定问题。而集合论在当时已被公认为现代数学的基础。

如何解读这个著名的罗素悖论？数学家们进行了长达一个多世纪的激烈争论，史称“第3次数学危机”。客观地说，这次争论促进了现代数学的大发展，也引发了集对(Set Pair, SP)概念的形成和联系数(Connection Number, CN)的诞生。

因为在罗素悖论中，可以同时用A,B2个集合去描述理发师所称的“全体服务对象”。把确定需要理发师理发的人放入确定的集合A，把理发师放入另一个集合B，由于理发师自己由谁理发不确定,为此给B乘上一个表示不确定的示性系数i，i在[–1,1]区间视不同情况取值，借此表明集合B的不确定性，再把A和Bi联 系起来组成集对H=(A,Bi)，既方便直观，也简明易懂。其中有3个关键点，一是用2个集合(一个确定的集合A与一个不确定的集合B)去同时描述同一个对象，而不是“一一对应”地用一个集合描述一个对象；二是让具有不确定性的集合B乘上一个不确定取值的示性系数i，使得具有内在不确定性的集合B在外表上与集合A一样有确定的形式，这种确定的形式使得集合A与集合B能够在一定条件下作相对确定的运算，如A ∩B,A ∪B等的同时，又使集合B的不确定性因i的作用得到外显，便于借助i对B做不确定性系统分析，形式上通过不确定性系统分析确定i的值；三是用一个联系符“⊕”把集合A与集合B联系起来组成一个数学表达式

不致引起误解时，把“⊕”号外面的圆圈省略，得到形如

的2元联系数。

类似地，当罗素所说的村子里又来一位理发师时，用3元联系数

表示有2位理发师竞争时的顾客人数分配，其中C表示确定由新来理发师理发的顾客人数，j=-1，表示A与Cj具有正负对立性；

以此类推，一般地，用n(n=2,3,...)元联系数

表示罗素说的村子里来n-1(n=2,3,...)位理发师时的顾客人数分配，n→∞时称u为无穷多元联系数。

从博弈论角度看，式(4)是一个多方博弈模型；从信息传递角度看，式(4)是一个无穷多个联系分量与各种不同场景共同决定的联系场；从时空角度看，这个联系场是既有确定性又有不确定性的D-U时空；由于式(4)中没有出现时间参数t(time)，因此是一个含有隐变量t(time)的结构函数，后面提到的偏联系数计算也利用了这个隐变量。

罗素悖论的集对解读，表明在数学中引进集对和联系数是必要的。这2个概念的定义如下：

定义1 由2个有一定联系的集合(事物)组成的系统，称为集对。

定义1说明集对是一个系统，且恰好是由2个要素集组成的元系统，罗素悖论中的理发师与顾客就是一个元系统。不难看出，以集对为基础，可以构建起包含智能系统在内的任意一个系统，等等。

定义2 集对中两个集合在不同层级上确定的关系测度与不确定关系测度组成的结构函数称为联系数。

定义2表明，联系数是集对的特征函数，一种同时具有确定性与不确定性双重特性的结构函数。式(2)—式(4)所示的2—5元联系数是目前常用的联系数，其中A,B,C,D,E,...∈R+，称为联系数u的联系分量，i,j,k,l,...称为联系分量B,C,D,E,...的不确定性示性系数，在[–1,1]区间视不同情况取点实数 或 区 间 数， 即i,j,k,l,...∈[-1,1]， 显 然u ∈[-∞,∞]。

当且仅当对式(5)中的bi作忽略或展开时，得到如式(6)的“正负型归一化联系数三角形”

式(6)、式(7)所示联系数有以下性质：

(1)系统性，从1元到无穷多元联系数是一个系统，其中的每一元联系数是联系数系统中的一个子系统，1元联系数a可以看作是隐去其补数(1–a)i的联系数；

(2)层级性，联系数系统中的每个联系数都处在一定的层级，单个联系数中的n个联系分量也处在从+1～–1的不同层级；但式(4)所示的无穷多元联系数中的无穷多个联系分量，则处在从+∞～–∞的不同层级；

(3)不确定性，通常，当一个联系数的首项与末项确定时，中间的各项具有不确定性；必要时，首项与末项也可展开，展开时的分界线通过调试确定，以满足问题求解的精度要求；

(4)方程性质，联系数是一个关于其中的不确定性示数取值待解的不定方程；

(5)质性性质，n(n≥2)元联系数中的n(n≥2)个联系分量是对研究对象不同质的测度刻画，或同一质的不同层级测度的刻画；

(6)几何特性，当联系数中的n(n≥2)个联系分量恰好能构成一凸多边形时，具有该凸多边形的几何特性； 在n个联系分量不能构成一凸多边形时，可以通过联系分量的不确定性示性系数取适当的值，实现凸多边形构图，进一步利用图形的几何信息求解相关问题；

(7)向量特性，把n(n≥2)元联系数放到n(n≥2)维向量空间中，做向量运算与向量分析；

(8)演化性；n(n≥2)元联系数中的n(n≥2)个联系分量在一定条件下相互生成和演化，从一个状态演化到另一个状态，其能量守恒(n(n≥2)个联系分量归一)；

(9)分形性，n(n≥2)元联系数中的n(n≥2)个联系分量，每个联系分量都可以在下一个层次上分解出本原联系数；

(10)传递性，n(n≥2)元联系数中的n(n≥2)个联系分量，都存在从首项到末项或从末项到首项的信息传递，也存在联系分量大的项向联系分量小的项的信息传递，或反向传递；

(11)能量特性，n(n≥2)元联系数中的n(n≥2)个联系分量，存储着一定的系统信息能；

(12)量子特性，根据性质(10)和性质(11)可知联系数具有量子特性。

联系数还有其他性质，因篇幅原因，不再一一叙述。

除罗素悖论外，自然辩证法的“对立统一”、“量变质变”、“否定之否定”3大定律与现代物理学中的海森堡(Heisenberg)“测不准原理”和能量守恒定律，以及“人生2只眼睛”等自然启迪也是集对与联系数的来源[10–12]。

2.2 集对论的基本原理与理论

2.2.1 基本原理

(1)成对原理：事物或概念都成对存在[13]。

时间与空间、物质与能量、物质与信息、能量与信息，对立与同一、对称与守恒、确定性和不确定性、关系与联系、联系与运动、运动与静止，整体与局部、简单与复杂、有限与无限、离散与连续、有机与无机、系统与环境、逻辑与直觉，原子与电子、分子与原子、电与磁；人的2只眼睛、2只手、2条腿、2只耳朵、以及腹背、肝胆、心肺、肠胃、气血、经络、心脑、毛发，等等；都是成对存在的例子。

从哲学看，成对原理的实质是哲学关于事物普遍联系与对立统一的换一种说法。

在一些实际问题的研究中，有时为节约资源，可以利用成对原理，隐去成对的其中一方，仅对没有隐去的一方做计算，对研究结果做分析时，则根据成对原理和归一化要求复现另一方，以利于做全面分析，得到与实际吻合的结论，后面提到的联系数隐形计算就是利用成对原理和系统能量守恒约束的一种绿色智能算法。

(2)不确定原理：事物的不确定关系(信息)与确定的关系(信息)对立统一、是个不确定性系统。

上述不确定原理与物理学中的海森堡(Heisenberg)“测不准原理”相通，区别在于后者仅说明微观粒子的位置与动量不能同时被确定，反映的是微观客体的特征； 但前者还表明宏观系统，如圆，以及边长确定为1的单位正方形中也存在不确定性等。

(3)相互作用原理：系统中的元素存在相互作用。如罗素悖论中的理发师与顾客，电场中的电磁感应等；联系数中的各个联系分量存在相互作用，以至于看上去是离散的联系分量其实是由多个联系波叠加振荡着的波函数；系统与系统所在环境也存在相互作用，作者在2023年8月召开的第17次全国集对分析学术研讨会上提出的共轭联系数就是用于系统与系统所在环境相互作用的一种新的联系数等。

(4)生成原理：集对中的2个集合在一定条件下通过相互作用生成新的集合，以偏联系数为代表的联系数伴随函数就是在一定假设条件下，通过特定相互作用而生成的一类新的联系数。

(5)系统信息能转化与守恒原理：世界是物质与能量的统一，信息是物质与能量相互作用的产物，信息具有能量，系统及其信息能既不凭空产生，也不凭空消失，但会从一种形式转化为另一种形式，或者从一个系统转移到别的系统；系统信息能在产生以后及其转化或转移过程中总量保持不变。集对的特征函数联系数是一个系统，联系数携带的系统信息能在联系数的运算过程中会获得算法所赋予的能量，但总量保持不变，由此引出联系数的系统信息能守恒算法，可以检验算法的科学性和规范性，也为算法的优化与机器学习提供约束和思想指导等。

2.2.2 基本理论

(1)不确定性系统理论。核心思想是把系统中确定的关系(信息)与不确定的关系(信息)看成是这个系统的一个子系统，在这个子系统中，确定性关系(信息)与不确定性关系(信息)相互联系、相互制约、相互作用，又在一定条件下相互转化，在转化过程中系统信息能守恒；以及基于能量守恒思想、把热力学熵、信息熵、负熵、等熵概念联系整合成一个熵系统的“联系熵”，以及各种熵概念在联系熵系统中的相互转换；以及对1阶不确定、2阶不确定、3阶不确定······直至无穷阶不确定的描述和处置等，有10多个要点，详见文献[4,14]。

(2)同异反系统理论。同异反系统理论是不确定性系统理论的极限理论，也就是把系统的某种不确定性极限看成是某种有确定意义的“反”。对常见的“反”给出了一种基于数学特征刻画的分类。分成正负型互反(1×(–1)=–1)、有无型互反(1×0=0)、倒数型互反(R×(1/R)=1)、互补型互反(P+Q)=1)、虚实型互反，以及“间隔型互反”(本级与隔级互反)，“顺逆型互反”(顺时针与逆时针互反)等；介在两个互反集之间的测度具有对应的不确定性，采用相应的不确定性示性系数表注其中的不确定性，借此与集对论的不确定性系统理论衔接；复杂性在于同异反可以相互嵌入对方，如同中有同、同中有异、同中有反，异中有同、异中有异、异中有反，反中有同、反中有异、反中有反，并在一定条件下相互转化，同异反系统理论也简称同异反理论，在技术层面上的应用称为同异反技术，详见文献[15,16]和后面的3.9节同异反技术的应用。

2.3 集对论的基本思想方法与基本算法

2.3.1 基本思想方法

(1)自然辩证法。自然辩证法中的对立统一律、量变质变律、否定之否定律，是集对论的基本思想方法和基本研究方法，但实践表明，在一个具体问题的研究中要自觉遵循自然辩证法3大定律并不容易。

(2)系统分析法。包括整体结构分析法与局部结构分析法、层次分析法、以及系统与元素、系统与系统、系统与环境的相互作用分析、全局分析等。

(3)综合集成法。同异反综合集成、确定的计算与不确定系统分析综合集成、集对论+非集对论综合集成等，以便于各种不确定性问题研究。

(4)具体分析法。由于D-U时空至少1维有不确定性，该时空中的事物也因此具有不确定性；具体的不确定性问题种类不一，情况各异、步移景换，因此集对论提倡“同类异法”“一题一法”“多法一题”；例如，3元联系数u=A+Bi+Cj中的不确定性示性系数i一般情况下在定义域[–1,1]中取值，i ∈[-1,1]，但也可以在特殊情况下到定义域之外取值，i ∈[-∞,+∞]，以适应极端反常因素突变出现一类问题的数学建模需要；从定性意义上说，在随机、模糊、信息不完全、不确知、涌现、突变等多种不确定性因素共同起作用的场合，不确定性示性系数i起不确定性因素“集成器”“分类器”和“转换器”的作用，当把联系数用于实际问题研究时，又起到理论研究结果与实际情况“对接器”和“调节器”“适应器”的作用等。总之：“具体问题具体分析”是集对论的灵魂。

(5)实践检验法。实践是检验真理的标准。也是检验集对与联系数模型与各种联系数算法与不确定性系统分析法的科学性、可信性的标准。阶段性的实践检验也称“反馈检验”，简称“反馈法”，可参考经典控制论；联系数模型的理论研究结果需接受实践的多阶段检验和反馈，才能检验模型计算结果的可信性测度a和不可信性测度c以及可信与不可信不确定性测度b的分配是否合理，才有可能使集对论的理论研究结果高度逼近各种事物在DU空间中演化的真实图景和遵循的规律。

2.3.2 基本算法

(1)联系数的普通四则运算[17–22]，见表1所示。

表1 以2个2元联系数与3元联系数为例的普通四则运算

(2)复联系数的向量运算[23–25]，如表2所示。

表2 以2元联系数为例的向量运算

(3)赵森烽克勤概率计算[26–31]，如表3所示。

表3 赵森烽克勤概率的常见运算

(4)不确定性的系统分析。联系数的上述基本算法不复杂，进一步的导出运算也不难，难点是其中的不确定性分析。以3元联系数µ=a+bi+cj,a,b,c ∈[0,1],a+b+c=1,i ∈[-1,1],j=-1为例，表面上看，对不确定性系统分析需从数学形式上对µ中不确定性示性系数i做取值分析，其实是对µ中不确定性联系分量b及整个3元联系数整体的不确定性系统分析，只要注意到3元联系数µ的取值区间是[–1,1]，即µ∈[-1,1] ，与i ∈[-1,1]同一区间；物理意义是对联系数刻画的事物在D-U时空中的不确定性与确定性相互作用做实时分析；因此，无论对于i做定量确定，还是做定性确定，如上一节中提到不确定性示性系数i在多种不确定性共存起“集成器”、“分类器”、“转换器”、“对接器”、“调节器”、“适应器”作用等，说到底，要到联系数所刻画的事物在真实世界中的D-U时空中去做反复确定，过程结束时才得到最后的确定，可以参见文献[3,4,14,15]等，也可以在下面的第3节中领会这里的意思；4.2.3节中提到把3元联系数u=A+Bi+Cj作为二极管的一种数学模型时，其中的Bi相当于二极管的基极，如此等等；可见这里说的“不确定性的系统分析”与2.3.1节中说的“具体分析法”一脉相承，是一种着眼于联系数做数学计算同时又着眼于联系数所在真实世界的D-U时空做物理分析、事理分析、哲理分析和逻辑分析的综合不确定性系统分析，也包括数学分析中的实分析、复分析、泛函分析、概率分析、相似分析、几何分析等等分析[32–35]，目的是让集对论的理论研究结果符合实际。

3 集对论在人工智能中的若干应用

3.1 在人工智能来源探讨中的应用

什么是智能？智能从何而来?这是人工智能研究中首先要回答的问题。文献[7,8]中给出的智能定义是，“智能是系统存在和发展并与环境联系的一种能力”。由于系统在自然界和人类社会中普遍存在，根据以上定义可知,自然界中的系统具有智能，夏天清晨池塘中荷叶上的露珠、电与磁的相互作用和能量转换、物体碰撞时的作用力与反作用力，一年四季的交替，等等，是自然系统具有智能的例子；人们借助迄今为止所认识和掌握的诸多自然科学原理、包括物理学原理、化学原理、生物学原理等知识，就是对自然系统智能认知的知识，人们又把这些知识经人脑加工和实践检验，形成人的智能，再通过一系列的算法把人的智能赋给机器，得到所谓的人工智能。反过来又协助人脑提高人的智慧，作者在 文献[7,8]中提出的“智脑”便应运而生。可见，自然智能是人工智能的导师。

3.2 集对论在载人航天器综合测试数据评估和雷达信号处理中的应用

中国空间技术研究院魏邦友在文献[36]中，把成功型号测试结果构建为集合X，将待发型号测试结果构建为集合 Y进行集对分析，并与传统评估方法结合，得到了一种新的载人航天器测试数据评估方法，通过对载人航天器地面综合测试阶段的测试数据进行分析,从而快速判断其当前状态是否满足发射及飞行任务要求。

刘以安等人在文献[37–40]中把集对分析及其偏联系数用于多雷达信号分选，仿真显示分选效果满意。

多部雷达在探测目标时，因受低空杂波、电子干扰和雷达自身探测精度等影响，易使部分雷达的探测数据不可靠而造成融合中心数据处理精度的下降。针对这一问题，刘以安等人[37–40]提出了一种应用多次融合数据为特征的集对分析思想，把每时送入融合中心的各雷达探测数据与1次融合后的数据组成集对，求出目标状态当前时刻的区间估计，去掉每时落入估计区间之外的雷达探测数据，再作2 次融合或更多次融合。仿真结果表明，应用集对分析能实现多雷达探测数据的择优融合，不仅算法简单，且能有效提高不确定多雷达系统的跟踪精度和可靠性。

文献[41]把基于集对分析法的顺序差直方图分选算法SpaSDIF与改进SDIF分选算法做了对比，在脉冲数较少时，两种方法仿真时间差别不大。随着脉冲数的增加，基于集对分析的SpaSDIF分选耗时为0.2 617 s，而 改进SDIF算法的时间消耗显著增加，总耗时为2.546 s，前者比后者效率提高9.7倍以上，且具有分选准确率高、实时性好等优点，有助于提高电子对抗系统的实战能力。

殷志远等人[42]用集对分析方法确定雷达估算降雨场的Z-I关系，把雷达估算降雨和雨量站网格插值降雨进行同异反对比分析,结果表明,集对分析较现有方法优越，其中的关键是对“同”、“异”、“反”的界定做反复调试，从而得到最优聚类。

孟现海等人[43]给出了基于集对论数字空间尺度理论和联系数态势的图像边缘检测算法，实验结果表明该算法不仅计算速度快,而且检测的目标边缘准确、清晰，且对噪声的抑制能力强。

3.3 集对论在复杂系统智能预测中的应用

复杂系统在不确定性环境中的状态评价与趋势预测在不同领域有不同的问题表达和不同的难度。集对论在这方面已有若干研究成果，形成了“基于集对论与非集对论集成的确定的数学建模+不确定性系统分析”的系统智能预测模式，这方面的综述见文献[44]，这里简介该模式中的3个应用实例。

实例1 天气降水预报。

天气系统是同时具有确定性和随机不确定性双重特性的复杂系统。基于概率的多元回归模型(Regression Estimation of Event Probability,REEP)是世界各国进行天气预报的基本模式。由文献[45–47]知，王国强在1998年就把集对论用于天气降水预报多元回归模型REEP的改进研究，通过对进入预报模型的预报因子及其数值按集对论进行预处理，提高了天气降水预报的准确率，在对93次个例的降水预报作回顾性检验时，81次预报结论不变，有12 次修改了预报结论，其中11次修改成功，1次修改失败,成功率0.917，如表4所示。

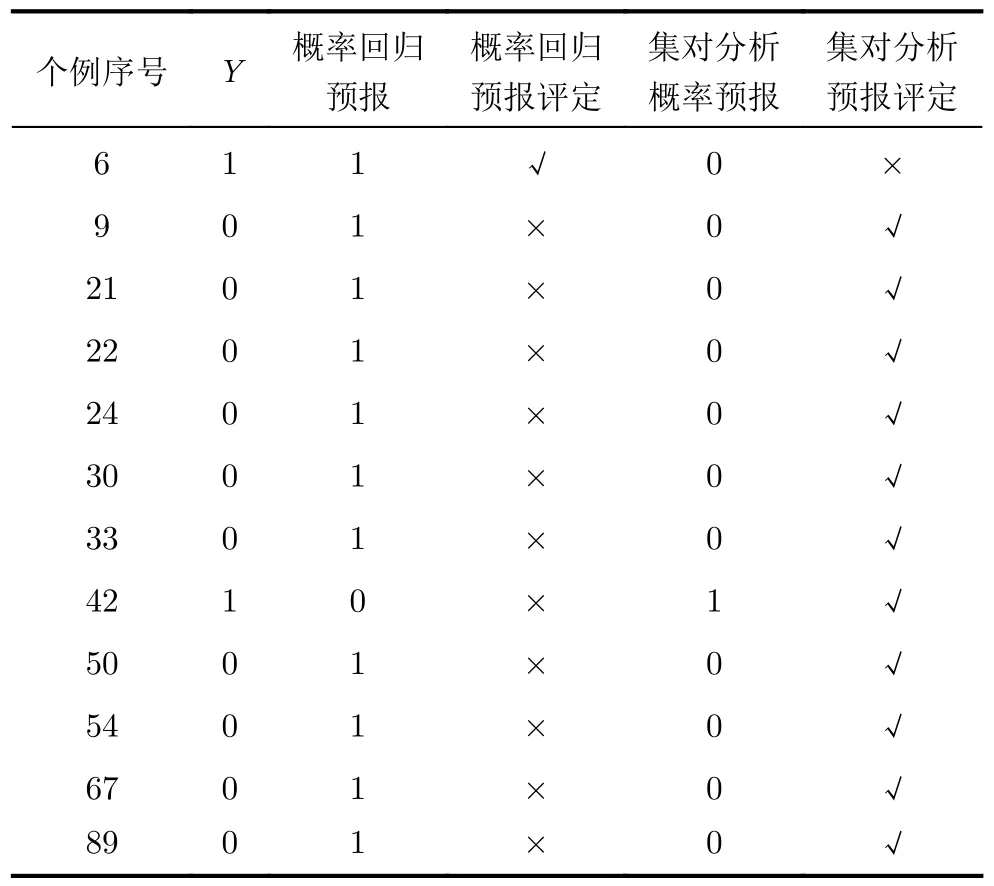
表4 集对分析对REEP的修改效果

预处理的基本步骤是：首先，在众多的气象要素中确定预报降水事件W的n个“最佳因子”集合(做中长期降水预报涉及的因素多达10多个，短期和近期降水预报涉及的因素较少，如取n＝5)，但这n个“最佳因子”在每一次降水预报中对指示W所起的“作用”强(大概率)弱(小概率)不是固定不变的， 而是一个动态变化着的组合；为此第2步，计算这n个预报因子在每一次降水预报中的变异系数，按变异系数从小到大把n个预报因子分成“同”(指示事件W出现)、“异”(指示事件W出现与否较模糊)、“反”(指示事件W不出现)3类，把变异系数最大的因子被认为是指示降水事件W的弱势因子，该弱势因子会干扰其他强势因子指示降水事件W的出现；为此第3 步，把弱势因子的数值按集对论中的“i比例取值原理”分解给强势因子，加强预报模型做出降水事件W出现的概率，当对历史数据做回顾性预报结果不满意时，需对前述的“同”“异”“反”界定作出调正，还要对i的取值做出调整,也就是对其中的“异”做出最合理的分解，调试满意后再利用模型做出预报，从而使每次降水预报都逼近理想预报。

实例2 水库滑坡变形预测。

刘晓等人[48]把集对分析理论(Set Pair Analysis Theory, SPAT)与模糊马尔可夫(fuzzy-Markov)理论结合，对滑坡(SPA)模型中的不确定系数i进行2次建模预测······结果表明：复合模型能够进一步提高对刘家沱水库滑坡变形进行整体预测的精度，在岩土监测分析领域中具有良好的实用价值。

实例3 隧道施工突涌水风险预测。

许增光等人[49]把集对论与层次分析法和最大隶属度原则结合预测跃龙门隧道下穿高川河浅埋段的突涌水风险，计算结果显示，危险性评价预测的突涌水量范围为3 000～10 000 m3/d，现场开挖实际涌水量为7 000 m3/d。

3.4 集对论在贝叶斯概率推理中的应用

文献[30]为研究贝叶斯概率与其后验概率的联系与转化以及联系数化后的贝叶斯推理，定义了贝叶斯概型的赵森烽-克勤概率，其数学形式为a+bi2元联系数，等同于古典概型、几何概型、频率概型的赵森烽-克勤概率，借助a+bi中随机转换器i的作用，把贝叶斯概率的后验概率分为增益型、衰减型、维持型，在此基础上给出贝叶斯概率向赵森烽-克勤概率转换定理与相应算法，用伊索寓言中孩子与狼的故事说明贝叶斯概型的赵森烽-克勤概率具有智脑思维的完整性、前瞻性和灵活性等特点，计算公式见表3。

3.5 在不确定性决策中的应用

不确定性决策是人脑基于确定性与不确定性对立统一思维的一类智能决策。文献[50,51]综述了把区间数转换成联系数后的不确定性决策，文献[52]综述了集对分析在纯自然语言决策，自然语言与数学混合语言决策，区间数决策和直觉模糊决策，集对分析粗糙集决策，联系数与马尔可夫链相结合的决策，基于赵森烽-克勤概率的贝叶斯决策，基于偏联系数的破案型决策、同异反综合集成决策等方面的应用。文献[53]基于同构的思想给出了多型异构数据下准则具有优先级别的双边匹配决策；等等；总起来看，集对论在不确定性决策中的应用较为灵活，适用性好，可操作性强、具有以下特点：(1)把基于确定性的决策建模与不确定性系统分析决策结合，(2)把系统宏观层次的分析与微观层次的分析结合决策，(3)静态决策与动态决策结合，(4)把“基于集对论的决策与非集对论决策”集成，根据不确定性的具体情况给出前瞻决策建议或延缓决策建议，是一种立足于全局和前瞻性的智能决策； 从D-U时空角度看：基于集对论的不确定性智能决策过程，本质上是把决策系统中的系统信息能转换成计算智能和系统分析智能的过程，是一种能量转换过程型决策，因此有所谓的初决策与终决策结合，1次决策与多次决策结合等过程型特点，不足之处是相应的决策算法不够固化和通用。

3.6 在人工智能基础研究中的应用

(1)人工智能从上世纪50年代提出以来，长期在实用价值的引导下对人工智能基础多头探索，形成符号主义、联结主义、行为主义3大学派；近年，著名人工智能专家钟义信教授等人相继提出“机制主义”“信息主义”和“通用人工智能”[54]；ChatGPT的出现，使“通用主义”为大众接受；显然，不同的“主义”都得遵循对立统一、量变质变、否定之否定3大定律，都用得上这3大定律的数学模型，都用得上集对论的成对原理和不确定原理，因此，集对论是对上述人工智能基础研究“5大主义”的一个支撑。

(2)前面提到罗素在集合论中要让所有“不属于自己的元素”组成一个集合，从而引出悖论，实事求是讲，“不属于自己的元素”并不是一种特殊情况，而是一种普遍现象，例如说“1个电子”，这个“1”本质上属于“电子”而不属于1； 说“2条信息”，这个“2”本质上属于“信息”不属于2；说“3个人”，这个“3”本质上属于“人”而不属于3，而人是社会关系的总和，是一个复杂概念；同理，“电子”与“信息”也没有确切定义.即使说“1个1”，前面这个“1”也属于后面的1，如此等等，产生这种现象的根本原因是客观事物本身相互联系，属于自己和不属于自己的2种属性成对存在；因此，对于上面说的“1”,“2”,“3”，充其量只能用辩证的语言说“既属于自已又不属于自已”，如何用数学形式描述这些“既属于自已又不属于自已”的数字，是一件相当困难的事；但集对论为我们提供了一个可行的办法：就是把他们写成联系数的形式，例如写成1+1 i,2+2i,3+3i···等，如有特定约束条件，则按约束条件写出已知数的不确定性伴随数，得到一个在特定条件或特定范围内的“既属于自已又不属于自已”的联系数，参与进一步的数学建模与数学运算。

例如自然数0,1,2,3,4,5,6,7,8,9，如按十进制约束，得用10做为论域上界，于是写成0+10i,1+9i,2+8i,3+7i,4+6i,5+5i,6+4i,7+3i,8+2i,9+1i；也可以根据问题要求选定其他数做为论域上界。例如要计算3人组成的群体智能，把3做为论域上界，每个人在3人团队中的智能是1+2i，其中1表示这个人自身智能，2i表示其他2位对这个人的影响，3个人的总智能是3+6i,当i=1时，这个3人群体总智能是3+6i=9(“3个皮匠抵个诸葛亮”)；当i=–1时，这个3人群体总智能是3+6i=–3(“3个和尚没水喝”)；当取i=0时，3+6i=3(3人群体智能没有产生“整体大于部分之和”的涌现)；当i在[–1,1]区间取其他值时，3+6i在[–3,9]区间取各种值(表示3人群体在一般情况下可能产生的各种智能)；特别地，当i在[–1,1]区间之外取值时，3+6i的值域为[–∞,∞]；这里，既考虑i在定义域内取值，又考虑i在定义域外取值的情况，也是集对论的题中之义。即把i ∈[-1,1] 做为集合A，把i∈/[-1,1]做为集合A¯ ，(A,A¯)组成一个集对做集对分析。

自然数的联系化使得一些有关自然数的自然语言能够用联系数表达，例如某道工序需要5 d左右时间完成,可以表示成5+Bi,其中的B=1,2,3,…根据问题的具体情况定，i在[–1,1]区间视不同情况取值，使工程施工管理用网络计划符合确定-不确定性时空(D-U时空)中的施工管理科学化、智能化要求[55–60]。文献[61,62]利用A+Bi型联系数创建了作物同异育种理论和作物同异育种智能决策系统。

自然数的联系数化使得已成习惯的自然数排序成为基于联系数不确定性排序的一种特例，后者的排序需经不确定性分析才能确定，例如3(+7i)有可能排在2(+8i)前面，违反了2在3前面的传统排序，因为不等式3+7i≤2+8i中的2个i可以取不同的值使不等式成立，这类被联系数化的自然数排序的不确定，显然需要“具体情况具体分析”。

事实上，国际标准化委员会(International Standardization Organization, ISO)在1993年就公布了关于测量数据需要标注测量不确定度的标准《测量不确定度表示指南》，我国在1999年原国家质量技术监督局批准并发布了与ISO)1993等效的JJF1059-1999《测量不确定度的评定与表示》技术规范，其实质就是A+Bi型联系数的表达。

不少学者对于自然数的2元联系数表示及其应用颇感兴趣，从不同角度进行了探索。如文献[63]研究了观察数据用联系数表示的最小二乘法及应用，认为通常观察数据由观察值和观察误差两部分组成.因此可以用联系数作出客观描述，在此基础上给出了一种新的最小二乘法，比传统的最小二乘法能更细致地分析偏差的平方和，从而更精确地得到经验公式。文献[64]试把群论引入到联系数的运算，提出了联系数群的概念。文献[65]把联系数中的联系分量用2元联系数表示，提出多元两重联系数，把其用于汽轮机故障诊断。文献[66]把2元联系数与投影灰靶决策理论结合用于电网应急能力评估。文献[67]定义了区间数集对2元联系数，利用区间数长度、集对、同一集、差异集以及比较空间的3个特征量，构造了基于2元联系数的可能度函数，进而建立了基于2元联系数可能度函数的区间数排序方法，较为客观地反映和描述了区间数相对大小比较时的确定性信息与不确定性信息.通过2元联系数的可能度函数性质证明和实例分析，证明2元联系数的可能度函数的有效性，保序性和广泛适用性。

由上可见，自然数的2元联系数表达在理论研究和应用研究两方面都有广阔的应用前景。

按文献[68]的观点，当前的人工智能以“算力、算法、算例”为基础，从这个角度看，集对论也是当前人工智能基础的一个支撑。

3.7 在网络研究中的应用

人是人类社会的特征，从人脑走出来的网络是时代的特征。网络改变了社会，改变了人与人之间的联系方式，成为人工智能研究的前沿。文献[69]给出了基于集对论的社会网络α关系社区及动态挖掘算法，文献[70]为解决具有不完备和分类型矩阵数据集的聚类问题，同时考虑样本和类簇间的不确定关系，提出了一种面向不完备分类型矩阵数据的集对k-modes聚类算法，文献[71]综述了集对论在基于不确定性理论复杂网络建模方法研究中的进展，文献[72]提出了基于集对论的物联网三重社区发现算法，文献[73]给出了一种基于集对分析的P2P网络安全信誉度新算法，文献[74]建立了一种基于集对论的P2P网络声誉评估模型。文献[75]把集对分析用于以内容为中心的网络缓存放置策略的多准则群决策研究，文献[76]把集对分析用于网络中顶点间相似性度量方法研究，等等；但网络在确定不确定的D-U时空中不断延伸和时变，有更多更复杂的问题需要研究。

3.8 与神经网络融合的应用

文献[77]把径向基函数(Radial Basis Function,RBF)神经网络和集对分析融合做风电功率超短期预测，文献[78]把集对分析与RBF神经网络融合构建生态文明建设评价指标体系，文献[79]把反向传播(Back Propagation, BP)神经网络与集对分析(Set Pair Analysis, SPA)结合用于地铁隧道掘进机(Tunnel Boring Machine, TBM)施工安全风险评估，文献[80]基于集对分析和遗传BP(Genetic Algorithm-BP, GA-BP)神经网络做地下水埋深预测研究，文献[81]给出集对分析与径向基函数神经网络融合的预测模型用于水文预测，文献[82]建立了一个基于BP神经网络和集对分析的城市智能增长计划的评价模型，在评价结果的基础上，为未来城市的智能开发作出更好的新规划，等等。

上述文献中的工作，如果能对输入数据预处理成2元联系数或多元联系数，将使神经网络深度学习获得更丰富的信息，提高学习效率。

3.9 同异反技术的应用

同异反是集对论基于对立统一及其中介过渡哲学理念而提出的一个概念。同异反技术是集对论处理集合与集合之间既确定又不确定关系的一类技术，是集对论的同异反系统理论在技术层面上的具体化。包括同异反定义与同异反界定、同异反相关与不相关、同异反分类与同异反聚类、同异反分析与同异反综合、同异反模式识别、同异反设计与同异反规划、同异反信息与同异反控制、同异反演化与同异反转化、同异反集对与同异反集成、等等。文献[83]把基于集对论的同异反模式识别技术用于管道土壤腐蚀综合评价，文献[84]把同异反最优模式识别模型用于系统危险性评价，文献[85]给出了一种平面图象的同异反模式识别技术，文献[86]提出一种基于集对论的多数据流同异反分析法，文献[87]把同异反分析用于寻常型银屑病用药优选，文献[88]给出基于集对论的同异反知识创新规律，文献[89]就教学中的默会知识和显性知识做同异反集对分析；等等。由于集对论中的同异反概念是一个自叠加、自纠缠、自压缩、自嵌套的概念，所在的D-U空间是一个不规则空间，相应的同异反技术具有强大的灵活性和适用性，存在极大的发展空间。

3.10 在系统安全分析中的应用

文献[90]把联系数与故障树分析(fault tree analysis)结合用于建筑设备自动化系统(Building Automation System, BAS)可靠性分析，文献[91]把集对论用于金刚滚轮转动系统故障树分析，文献[92]把集对论及其偏联系数用于地铁隧道穿越地下管线风险趋势评估研究，文献[93]把集对论及其偏联系数用于工程过程安全的评价与分析，文献[94]给出了基于多因素集对分析的系统故障模式识别方法，文献[95]把集对论与量子物理结合研究系统多功能状态表达式构建及其置信度的计算,同时给出满足归一化约束的试验结果可信度、不可信度、可信不可信不确定度，为类似的系统多功能状态的完整表达提供了一种具有客观实在性的科学计算，展示出广阔的应用前景，也同时给出了集对论与量子物理结合，研究和处置D-U确定不确定空间中事物确定性与不确定性相互作用和演化规律的新途径，有重要的理论价值和实用价值。最近，Kamran等人[96]把集对论及其联系数用于化工过程工业中安全事故多米诺效应动态建模分析，对化工过程工业安全事故的防范和处置具有重要的思想指导和推广应用价值。等等。

3.11 中医辨证论治智能化研究中的应用

文献[97]最早把集对分析用于中医证候规范化研究，指出，“中医学中广泛存在着不确定性，其精髓也往往很难把握，随着科学的发展，中医证候的规范化研究成为中医界乃至整个科学界关注的问题。集对分析是一种用联系数a+bi+cj统一处理模糊、随机、中介和信息不完全所致不确定性的系统理论和方法，是把确定性与不确定性作为一个既确定又不确定的同异反系统进行辨证分析和数学处理。从量的角度去探讨中医证候，将集对分析应用于中医证候的研究中，是从系统层次的角度，领会中医学不确定性的本质，有可能会很大程度地推动证候规范化和中医客观化的理论研究”。文献[98]把集对分析联系数用于痛风性关节炎血瘀证辨证因子研究，文献[99]应用集对分析对慢性皮肤溃疡中医辨证论治规律数学建模，文献[110]把集对分析用于寻常型银屑病方证相关性研究，文献[101]把集对分析偏联系数用于寻常型银屑病对症用药优选，文献[102]把4元联系数用于土槐菝葜汤治疗血热型银屑病疗效研究，文献[103]讨论了基于集对分析的疗效曲线在银屑病血热证典型方剂选优中的应用，文献[104]对基于集对分析筛选的寻常型银屑病血热证诊疗方案临床效果进行研究，文献[105]探讨了皮肤病脏腑辨证的联系数学模型在临床中的应用，文献[106]探讨了联系数在银屑病治疗中医单方研究中的应用，文献[107]把集对分析用于凉血潜阳法治疗寻常型银屑病血热证的临床观察，文献[108]建立了基于六元联系数方程的六经辨治皮肤病模型，文献[109]把基于集对分析的阴阳平衡方程用于皮肤病诊疗研究，文献[110]应用偏联系数探讨银屑病的复发因素及预后趋势，文献[111]把集对分析态势值与疗效曲线用于银屑病血热证中药选优，文献[112]提出了一种基于高阶马尔可夫链和集对分析的糖尿病溃疡疗效预测方法； 特别是文献[98–110]的作者李斌、李欣、蒯仂等人从2015年起开始从临床应用角度检验前期集对分析成果的实际疗效是否有得到提高，通过近5年的临床实践证实了集对分析确实有助于中医辩证论治皮肤病疗效提高，以寻常型银屑病血热证诊治为例，集对分析成果组(59人)的临床有效率为88.14%， 传统中医组(58人)临床有效率为82.75%，西药组的临床有效率为67.24%；在此基础上撰写和出版专著《中医辨证论治集对分析》，先后编制5个软件：(1)高阶马尔可夫链集对分析疗效预测数据平台V1.0，2023SR0418254，(2)贝叶斯网络自学习扩展集对分析疗效评价数据平台V1.0，2023SR0396970，(3)多维云层次分析疗效评价数据平台V1.0，2023SR0397435，(4)基于集对分析偏联系数的中医诊疗系统V2.0，2019SR0840697，(5)银屑病慢病综合管理软件V1.0，2022SR1524121，供临床应用，为中医辨证论治智能化作出了重大贡献[113]。

3.12 其他应用

文献[114]提出基于集对论方法和理想解相似度排序技术，对V型海底隧道视错觉减速标线的有效性进行评价，文献[115–117]把集对分析用于水文水资源的评价预测，文献[118]给出了水文气象时间序列混合小波去噪秩次集对分析方法，文献[119]给出了一种基于集对论与证据理论结合的混合推理算法，文献[120]把集对论用于直觉模糊集相似度度量，文献[121]把集对论用于上海地面沉降研究，文献[122]把集对论用于高斯混合模型的模仿学习算法优化与评价，文献[123]把集对论用于智能居住适宜性评价，文献[124]把集对论试用于智能制造企业遇到的数字孪生绿色绩效评价研究，文献[125]把集对论用于纳米SiO2和PVA纤维地聚合物砂浆性能优化，文献[126]对1989年～2020年间的集对分析在环境科学中的应用与挑战做了文献综述，文献[127]就集对论与非集对论方法耦合应用出版了专著，等等。

上述表明，集对论+非集对论的广义集对论是集对论能够得到广泛应用和持续发展的一个有效思路。

4 进展与展望

4.1 进展

4.1.1 偏联系数及其应用

偏联系数是作者对罗素悖论中理发师与顾客可以互换空间位置深入思考，于2005年提出的一个联系数的伴随函数[128]，特点是：根据联系数当前状态的联系分量，在一定的假设条件下进行由果溯因式的计算与分析，回答系统的过去到当前状态的演化进程，由此测算系统从过去到当前状态的趋势，预测到达未来状态的可能性[129–131]。

例如环保部门监测某河流的当前水质，有50%的指标达到优质级，30%的指标达到合格级，20%的指标不合格；用3元联系数µ=a+bi+cj=0.5+0.3i+0.2j(a>b,b>c,a>c)(同势1级，强同势)表示监测结果，利用偏联系数算法能从这个监测结果回溯这条河流的水质从过去到当前状态的演化率，计算过程如下：

把上式归一化，记为µ∗，得µ∗=0.312 5+0.487 5i+0.2j(ac,a>c)(同势2级，弱同势)，µ∗就是这条河流水质从过去到当前状态的1阶正负全偏演化率联系数，与当前状态的监测结果联系数µ=0.5+0.3i+0.2j对照，可以看出过去属于合格级的指标由0.487 5减少到0.3，减少部分的0.187 5增加到优质级，使优质级从过去的0.312 5增大到现在的0.5，不合格级的20%保持不变，同异反态势由“同势2级，弱同势”提高到“同势1级，强同势”；由此得出结论：这条河流的近期水质在改善之中。

同理可以再进一步计算µ∗=0.312 5+0.487 5i+0.2j的1阶正负全偏联系数，得到µ的2阶正负全偏联系数µ∗∗,µ∗∗=0.195 3+0.659 2i+0.145 5j，由此看出这条河流在“过去”的“过去”时，优质级指标占19.53%，合格级指标占65.92%，不合格级指标占14.55%；总体看µ∗∗到µ∗到µ，虽然优质级指标的百分比值有0.195 3↑→0.312 5↑→0.5的演化趋势,但处在优质级与不合格级之间的合格级指标的百分比值仍较显著：0.659 4↓→0.487 5↓→0.3，整体演化趋势向好但有不确定性。不足的是，上述算法没有说明“过去”的“过去”与“当前”相隔的时间 ∆t有多大[132]，理论上会引发所谓的犹豫决策，但按文献[133–135]，此类犹豫决策仍可以用偏联系数处理。

人们会问，能否计算出µ∗∗的数值？以便根据数值大小决定决策；对此，文献[129]对µ=0.5+0.3i+0.2j先分别求µ的2阶偏正联系数∂2+µ与2阶偏负联系数∂2-µ的值，再求得µ的2阶正负全偏联系数∂2±µ数值为–0.005 9，回答了上面的问题，两者殊途同归：∂2±µ=µ∗∗，也就是0.190 5+0.659 4i+0.145 5j=-0.005 9，属于一种与正负临界趋势0有稍微偏差的演化趋势，说明了导致犹豫决策有一定的数量依据。从方程角度看，0.190 5+0.659 4i+0.145 5j=-0.005 9是一个2元1次方程，由于在正负型联系数的定义中已规定j=-1，据此可解得其中的i=-0.077 2。

文献[136]给出了反偏联系数的概念及其计算方法，即在已知3元联系数µ的2阶正负全偏联系数∂2±µ或1阶正负全偏联系数∂±µ的条件下，反求这个3元联系数µ；与已知一个3元联系数µ求他的1阶正负全偏联系数∂±µ和2阶正负全偏联系数∂2±µ计算互为逆运算。

由于一个3元联系数µ=a+bi+cj可以根据问题求解的精细化要求，对联系分量a,bi,cj做不同层级的分解，特别是对联系分量bi的不确定性分类与分解，解析成4元联系数、5元联系数、6元联系数···10元联系数···直至无穷多元(多级)联系数，因此可以计算无穷多个无穷阶次的偏正联系数、偏负联系数、偏中联系数、偏某些特定值的联系数和全偏联系数，每个阶次偏联系数中的不确定性示性系数又可以通过不同的理论假设，如哲理假设、物理假设、数理假设、事理假设、人理假设、情景假设等等，和不同的途径和模型取不同的值，客观上能对联系数所描述的事物做无穷多维度和无穷多层级以及无穷多时间点上的无穷个微分切片和计算，借助这无穷个微分切片上的联系数µn(n →∞)及其偏联系数∂nµn(n →∞)描述事物从过去到当前状态所历经的无穷多维度和无穷多个时空层次上的微观演化图景和微观演化规律，这与牛顿力学借助微积分描述事物在无穷多维度和无穷多层级以及无穷多时间点上的宏观运动规律做数学刻画正好宏微互补。以求某导弹飞行曲线上某点的飞行速度为例，牛顿力学把导弹视作一个质点，用导数的概念求此点的速度；集对论则着眼于导弹的内部结构，用偏联系数刻画导弹内部结构相互关系的演化趋势，扮演“内导数”的角色，相对地可称前者为“外导数”；如此等等。另外一个重要原因是前述3元联系数µ=a+bi+cj可以解析展开成式(6)或式(7)所示的无穷多元(多级)联系数；还有3元联系数µ=a+bi+cj中的“同一度a”与“对立度c”直接相互转化的同异反全偏联系数算法，由于比前面介绍的正负型全偏联系数算法复杂，这里不做具体介绍，可以参见文献[137–140]。

除偏联系数外，联系数还有势函数、态势函数、邻联系数、圆函数、三角函数、跳跃函数、碰撞函数、核函数、叠加函数、纠缠函数、共轭函数等其他伴随函数及其这些伴随函数的反函数，研究这些函数的特性和应用需要用到实分析、复分析、泛函分析、概率统计分析、几何分析、以及辩证逻辑等方面的更多知识，现有的应用因此需要进一步系统化和规范化研究，见文献[141–143]等。

4.1.2 联系数的系统能守恒算法

上节用3元联系数µ=a+bi+cj=0.5+0.3i+0.2j表示某河流水质在最近一次监测的结果，其中的3个联系分量满足归一化要求: 0.5+0.3+0.2=1,1阶演化率联系数µ∗=0.312 5+0.487 5i+0.2j中的3个联系分量仍满足归一化要求：0.312 5+0.487 5+0.2=1，可知偏联系数计算过程中曾获得算法赋予的1个单位的联系数能量而达到2个单位的联系数能量(0.625+0.975+0.4=2)(事实上是计算过程中每个联系分量被重复使用两次所致)，但在归一化计算后又扬弃了这1个单位的联系数(能量)，从而保证了一阶全偏联系数计算结果的归一化，可见上述计算的实质是一种基于联系数系统能量守恒的算法；类似地，对1阶演化率联系数µ∗=0.312 5+0.487 5i+0.2j再做1阶全偏联系数计算得到µ的2阶全偏联系数µ∗∗，同样有 0.195 3+0.659 2+0.145 5=1结果。研究表明，联系数的系统能量守恒算法能防治计算过程中联系数的系统结构信息不丢失，也为构造联系数的各种伴随函数提出了约束条件，例如3元联系数µ=a+bi+cj的势函数 shi(µ)在文献[5]给出的定义是 s hi(µ)=a/c,(a+c)≤1，2022年在文献[131]中 定 义 为shi(µ)=a/c+bi/c=(a+bi)/c,(a+b+c=1) ；当c=0 时，3元联系数µ=a+bi+cj退化为2元联系数µ=a+bi,(a+b=1)，这时的2元联系数势函数定义是 shi(µ)=a/bi，从而遵循了联系数的系统能量守恒约束，发展和完善了文献[5]给出的势函数定义。

文献[5]给出的3元联系数态势排序矩阵，也体现了联系数系统能量守恒(a+b+c=1)约束，见表5。

表5 3元联系数 µ =a+bi+cj,(a,b,c ∈[0,1],a+b+c=1,i ∈[-1,1],j =-1)的态势排序

表5揭示出3元联系数的3个联系分量之大小关系在数学形式与逻辑之间存在不协调现象，按“排列组合原理”应当出现33=27种a,b,c大小关系，但只有13种在逻辑上成立，其他14种在形式上应当出现但在逻辑上不能成立；其次是表5中的a,b,c大小关系在形式上忽略了b的不确定性，把b与a,c做了同样是确定性测度对待，弥补这一不足的办法是应用表5时要对b做不确定性取值分析，例如分别取-0.5b和 0.5b等等；检视这时的3元联系数态势级别变化，确定出态势的变化区间。

类似地，4元联系数µ=a+bi+cj+dk的4个联系分量a,b,c,d之大小关系按“排列组合原理”有34=81种大小关系，但只有部份大小关系在逻辑上成立；类似地，5元联系数µ=a+bi+cj+dk+el的5个联系分量a,b,c,d,e之大小关系按“排列组合原理”有35=243种大小关系，同样也只有部份大小关系在逻辑上成立···一般，n(n ≥3)元联系数的n个联系分量的大于(>)、等于(=)、小于(<)关系按“排列组合原理”有3n种大小关系，但只有一部份大小关系在逻辑上成立，提示在数学中，形式上的演算是否合乎逻辑需要一一考察，是否有一般规律可遵循，有待进一步研究。

联系数的系统能量守恒算法提示机器的形式化学习与形式化推理需要“逻辑检验”和“节能”，以最少的能耗实现最省时的高效率学习和获得最满意的推理结果并“合乎逻辑”，后面提到的联系数的“隐形计算”也与这里说的“节能算法”有关，辛普森悖论也与这里提到的“形式上的合规演算与逻辑是否一致”有关。

4.1.3 共轭联系数

共轭联系数是作者在2023年在线召开的第17次全国集对分析学术研讨会上提出的一个新概念，基本思路是根据第2 节中的“成对原理”考虑罗素悖论中有2个村的理发师悖论问题，引出同一时空中2个联系数(如2元联系数、3元联系数、4元联系数、5元联系数、直至无穷多元联系数)的各种联系如何计算才能得到符合实际的效果。共轭联系数是2个有共轭关系的联系数组成的一对联系数，基于集对论的2个联系数的共轭关系包括了2个联系数对应的联系分量具有共同关系、共异关系、共反关系：共同异关系：共同反关系、共异反关系、同转异关系，同转反关系、异转同关系、异转反关系；反转同关系、反转反关系，等等关系,概括地说，这些关系就是文献[15]中说的同异反关系。

共轭联系数为一般性地借助联系数研究系统与所在环境相互作用数学建模提供了新思路，也同时提出了在确定不确定D-U时空中多个联系数相互作用如何计算的问题。这类计算有时较为简便，以4.1.1节中的河流水质从原来的µ∗=0.312 5+0.487 5i+0.2j变到当前的µ=0.5+0.3i+0.2j为例，就可以认为µ∗=0.312 5+0.487 5i+0.2j受到一个共轭联系数µ′=0.187 5-0.187 5i+0j的作用(通过某种治理使合格级指标达到优质级)，相对应的共轭算法是这2个联系数直接做加法运算，得：µ∗µ′=µ；但有时较为复杂。

4.1.4 隐形计算

隐形计算指在联系数运算过程中，暂时隐去联系数中不确定性联系分量的一种运算，但需要根据联系数能量守恒等法则和有关约定，把运算结果又写成联系数的形式，补写上先前隐去的联系数中不确定性联系分量的运算结果，并做不确定性系统分析，在节约计算资源的前提下，得到符合实际的结论。

例如，两个2元联系数µ1=0.5+0.5i与µ2=0.6+0.4i相乘，先隐去各自的不确定性联系分量 0.5i和0.4i， 把剩下的0.5记为µ1·=0.5， 0.6记为µ2·=0.6，得µ1·×µ2·=0.5×0.6 = 0.3 ，再把0.3写成0.3+0.7i，原因是µ1×µ2=(0.5+0.5i)×(0.6+0.4i)=0.3+(0.5×0.4i+0.5i×0.6)+0.2i2=0.3+0.5i+0.2i2，当仅仅考虑联系数的确定性与不确定性而不计不确定性的幂次时，根据文献[20,22]，有i=i2=i3=...=in,(n ̸=0) 的简化规定，由此得µ1×µ2=(0.5+0.5i)×(0.6+0.4i)=0.3+0.5i+0.2i2=0.3+0.7i。

从隐形计算角度看，经典概率计算是一种隐形计算，可参见文献[26–31]。

4.1.5 绿色智能计算

集对论的前述算法与非集对论算法的综合集成称为基于集对论的绿色智能计算生态系统。包括集对联系数的普通四则运算、统计计算、耦合计算、平行计算、生成计算、叠加计算、逻辑计算、时空效应计算、知识创新计算、博弈计算、偏联系数计算、联系数系统能守恒计算，共轭计算、几何计算、隐形计算以及关于不确定性的中医辩证论治建模计算与分析等等，其中的算法用于不同问题的求解各有特色各有优势各有不足，但都是在一定条件下有可行性的计算，都能解决一些特定问题，集成后能解决一些复杂系统问题，特别是无穷多个联系数的相互作用计算为复杂系统和超复杂系统建模提供了新途径。绿色智能计算强调集成后的算法灵活性、可选择性、可进化性、可优化性和可简化性，以同时满足计算结果满足复杂问题求解结果的科学性与实践检验性，以及计算的经济性等等。绿色智能计算一词最早出现在文献[144]中，文献[145]中有专节简介，“绿色”指上述算法可以根据需要相互生成和相互转换，根据需要生成新的算法或加入新的算法，例如文献[113]中用偏联系数化解统计学中的辛普森悖论，也可以采用3.6节中自然数联系数法化解文献[146–147]的辛普森悖论和讨论因空间转换而出现的不确定性，视计算结果是否符合问题求解的精度和逻辑要求而终止计算；集对论的绿色智能计算系统是一般性地定量化研究D-U空间中事物的确定不确定性子系统在不同的空间层次和不同的坐标系中生存演化乃至进化规律的一个有机生态系统，对于前面提到的形式上的计算与逻辑的协调与否，系统在整体上的确定与不确定的相互依存等，需要坚持对不确定性“客观承认、系统描述、定量刻画、具体分析、实践检验”的研究方针。

4.2 展望

4.2.1 辩证逻辑的形式化

从逻辑角度看，集对论的思维优势在于其中的辩证思维，依据的逻辑在整体上是辩证逻辑，同时也兼具形式逻辑、数理逻辑和其他逻辑。辩证逻辑的形式化一直是逻辑研究中的难点；如何在集对论的范畴内给出辩证逻辑的形式化，是集对论要进一步研究的重要问题之一；根据文献[148]中关于辩证思维、辩证逻辑、辩证计算本质上是同一的观点，不难给出在集对论范畴内的辩证逻辑形式化，从而在一定程度上解决人们长期来只能辩证地思维而不能辩证地计算的问题，不仅回答作者在文献[10]中提出的自然辩证法是否有数学模型的问题，也有助于揭示人脑辩证思维和辩证决策的奥秘，促进新人工智能的实现。

4.2.2 集合论的提升与创新

集合论是现代数学的基础[149]，集对论研究集对中两个集合之间确定的关系与不确定关系的相互作用，在此基础上推广到3个集合、4个集合、5个集合直至无穷多个集合之间确定的关系与不确定关系相互作用的研究，相应的算法比基于集合论的确定算法复杂；集对论中集对与联系数及其算法所在的DU时空，是包括概率空间、希尔伯特空间、黎曼空间等空间相互叠加、纠缠和在一定条件下相互转换的既确定(给定尺度或给定需求范围)又不确定的空间(超过给定尺度或超过需求范围)，因此，理论上，集对论可以看成是集合论的一种进化和提升，数学是否以集对论为基础，迎来一个新的转折，有待深入研究，研究的每一个阶段性成果都会应用于人工智能。

4.2.3 半导体的联系数模型

文献[144]认为联系数是半导体的一种数学模型。最新研究发现3元联系数u=A+Bi+Cj与二极管可以互为模型，即3元联系数u=A+Bi+Cj可以看作是二极管的一种数学模型，二极管是3元联系数u=A+Bi+Cj的一种物理原型；类似地，5元联系数u=A+Bi+Cj+Dk+El与三极管互为数学物理模型等，基此，可以类比电子线路图研究集对论及其联系数的应用途径和效果调控；或反之，把集对论联系数用于有关电子与信息系统中的有关问题研究，如最近的文献[150]，针对高维数据中传统距离测量的局限性，提出了一种基于集对论的超图构造新方法；文献[151]把集对论用于无线传感器网络(Wireless Sensor Networks, WSNs) sinkhole攻击检测和防御策略研究等。

5 结束语

世界是确定与不确定的统一体，确定与不确定的相互作用又引发出复杂性。人工智能一直面临不确定性和复杂性的挑战；对研究对象的不确定性“客观承认、系统描述、定量刻画、具体分析、实践检验”的集对论及其联系数也因此在人工智能等领域得到若干应用，虽然其自身有不少问题待深入研究，但集对论+非集对论的广义集对论思想及其繁衍而来的联系数学和联系科学, 无疑能有效应对不确定性和复杂性挑战，特别是建立在集对论+非集对论基础上的绿色智能计算，会在新一代人工智能中得到更多应用。