考虑阶梯式碳交易机制的电化学储能与抽水蓄能协同调度优化
佟 曦, 陈 衡, 苟凯杰, 徐 钢, 刘文毅, 张国强
(华北电力大学 能源动力与机械工程学院, 北京 102206)
随着我国“双碳”目标的提出,各行各业都在积极开展碳减排工作。电力行业的碳排放量约占我国能源活动二氧化碳量的40%,减排潜力巨大,其低碳转型发展对于我国实现“碳中和”战略目标至关重要。为实现该战略目标,我国电力行业一方面进行火电机组的灵活性改造,提高机组调峰能力[1];另一方面大力发展风能、光伏等新能源发电技术,并且大规模接入电网,以减少化石能源等消耗[2-5]。由于风能、光伏等新能源具有出力不确定性,以及发电的间歇性和波动性,其大规模接入电网后,给电网的电压水平、运行控制等带来巨大困扰[6-10]。储能设备可以在时间和空间的尺度上快速进行能量调度,解决调峰难的问题,从而维持系统的稳定性,因此近年来备受关注和使用[11-12]。
研究碳交易机制对新能源电力系统运行优化的影响至关重要,陈锦鹏等[13]构建了综合能源系统(IES)模型,并且引入阶梯式碳交易机制,构建以购能成本、碳排放成本、弃风成本最小的低碳经济运行目标进行优化求解,验证了所提策略的有效性。陈彦奇等[14]提出了计及阶梯型碳交易机制的综合能源系统优化模型,以系统运行维护成本和碳交易成本之和最小为目标,分析典型日下不同基准碳价对系统运行方式和经济性的影响。王俐英等[15]将需求响应和碳交易机制引入综合能源系统运行调度中,并基于信息间隙决策理论(IGDT)构建了考虑阶梯式碳交易机制以及需求响应的综合能源系统双层随机优化调度模型,最后通过求解证明了所提系统的低碳环保。Cao等[16]提出了面向运营商和多个虚拟电厂(MVPP)的Stackelberg博弈策略,考虑阶梯式碳价格机制和双补偿需求响应机制,采用克里金元模型拟合虚拟电厂(VPP)的能量调度模型,最后分析了多个算例,验证了所提策略能够有效促进MVPP的能量互补和碳减排。
平准化度电成本(LCOE),也叫电力平均化成本,是用于衡量发电项目在其整个生命周期内每单位电力产生的平均成本,在研究系统经济性中起到了至关重要的作用。刘漂[17]从全生命周期角度研究了风电成本的构成,并针对现有LCOE模型提出了改进的LCOE分析计算模型,通过物理建模验证了所提出的LCOE模型的有效性。Mostafa等[18]建立了电池储能成本模型,并考虑了长期、中期和短期应用以及技术特征,使用储能平准化度电成本(LCCOS)和LCOE进行技术经济评估,此外,还对影响存储成本的控制因素进行了敏感性分析。Li等[19]建立了实现碳捕集与封存(CCS)一体化气化联合循环(IGCC)建模、预测和优化的计算方法,选择碳捕集率(CCR)和LCOE作为优化目标,评估了多目标优化的最优解集和碳交易市场的效果。
当前大多数研究只考虑单一储能系统接入电网的运行优化及配置优化,考虑储能系统LCOE的运营策略研究很少。因此,笔者构建了含火力发电、新能源(风能、光伏)发电,以及抽水蓄能和电化学储能的多能互补系统数学模型;同时,考虑LCOE及碳排放成本,引入阶梯式碳交易机制,以总成本之和最小为优化目标,利用MATLAB的Cplex求解器进行优化求解,并且设置不同场景及不同碳交易机制,以比较不同调度方式的优劣,最终提出成本最低、碳排放最少、收益最大化的电力系统下电化学储能及抽水蓄能的协同优化调度策略,为新型电力系统的储能规划提供参考,助力电网高效清洁化及经济最优化的发展。
1 阶梯式碳交易机制模型
阶梯式碳交易是在碳市场中设立多个不同层级的碳排放配额,每个层级对应不同的行业或行业细分。不同行业的企业拥有不同数量的碳排放配额,企业在交易市场上可以自由买卖碳排放配额。与普通碳交易模式相比,阶梯式碳交易模式的优势在于更精准地针对不同行业的减排需求,可以更有效地推动高排放行业的减排工作[20]。阶梯式碳交易机制模型主要包含无偿碳排放配额模型、实际碳排放模型和阶梯式碳交易模型[21]。
1.1 碳排放配额模型
所构建的系统中,碳排放源有燃煤机组及系统外购电力。所构建系统的碳排放配额为
ECEQ=ECFP+ESOP
(1)
式中:ECEQ为系统碳排放配额,t;ECFP为燃煤机组碳排放配额,t;ESOP为系统外购电力碳排放配额,t。
燃煤机组碳排放配额为
(2)
式中:Ee(t)为t时刻机组供电CO2配额,t;Eh(t)为t时刻机组供热CO2配额,t;T为周期;Δt为时间长度,h。
其中,t时刻机组供电CO2配额为
Ee(t)=Qe(t)×Be×F1×Fr×Ff
(3)
式中:Qe(t)为t时刻机组供电量,MW;Be为机组所属类别的供电基准,t/MW;F1为机组冷却方式修正系数;Fr为机组供热量修正系数,燃煤机组供热量修正系数为1-0.22×供热比;Ff为机组负荷修正系数。
t时刻机组供热CO2配额为
Eh(t)=Qh(t)×Bh
(4)
式中:Qh(t)为t时刻机组供热量,GJ;Bh为机组所属类别的供热基准,t/GJ。
系统外购电力碳排放配额为
(5)
式中:ηe为单位电量碳排放配额系数;Pbuy(t)为t时刻系统外购电量,MW。
1.2 实际碳排放模型
燃煤机组的碳排放量为
(6)
式中:EACE为燃煤机组的碳排放量,t;βe为燃煤机组单位电量碳排放系数,t/MW。
系统外购电力碳排放量为
(7)
式中:EPCE为系统外购电力碳排放量,t;βs为系统外购电力单位电量碳排放系数,t/MW。
不考虑新能源(风能、光伏)发电及各类型储能放电时的碳排放量,认为其碳排放量为0,则当其出力时,相当于给系统减少碳排放量。减少的碳排放量为

(8)
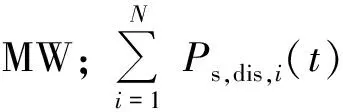
因此,系统的实际碳排放量EACT为
EACT=EACE+EPCE-ERCE
(9)
1.3 阶梯式碳交易模型
实际参与碳交易市场的碳交易额ECET为
ECET=EACT-ECEQ
(10)
当ECET大于0时,表示主体当前碳排放量高于碳排放配额,需要到碳市场购买碳排放配额;当ECET小于0时,表示主体当前碳排放量低于碳排放配额,可以将剩余碳排放配额拿到碳市场进行出售[22-23]。考虑经济效益最大化以及提高电力企业减排的积极性,构建阶梯式碳交易计算模型,即
(11)
式中:Ccar为系统的碳交易成本;c为市场的碳交易基准价格;d为碳排放区间长度;α为碳交易价格增长幅度。
传统碳交易机制下,其碳交易模型为
(12)
2 协同调度优化模型
2.1 LCOE模型
LCOE和全生命周期成本(LCC)都是在能源经济学和工程经济学中常用的概念,LCOE是衡量发电项目在其整个生命周期内每单位电力产生的平均成本[24],而LCC是衡量整个项目或设备在其寿命周期内的总成本。LCOE通常用于比较不同类型发电项目的经济性,而LCC用于做出长期投资决策,确保项目或设备的经济可行性。较低的LCOE意味着单位电力成本更低,使得该发电项目在市场上更具竞争力。在发电产业中,LCOE的下降通常与技术进步、规模效应和政策支持等因素有关。因此,LCOE被广泛用于评估各种发电技术的经济性,例如光伏、风能、煤炭、天然气等,以确定最具成本效益的能源解决方案。
LCOE的计算考虑了项目的总成本,包括建设、运营、维护、折旧成本等,以及项目预期的发电量[25-26]。这些成本在项目的寿命周期内被折算,然后除以预期的发电量,从而得到每单位电力的平均成本。
LCOE可以表示为
(13)
式中:CLCOE为LCOE成本,元;I为初始投资,包括项目前期规划建设以及设备购置安装等费用,元;On为第n年的运行成本,包括在使用阶段产生的费用,如能源消耗、人工劳动力、原材料等,元;Mn为第n年的维护成本,包括在使用过程中确保设备正常运转和良好状态的费用以及设备发生故障或损坏时所需的修理和维修费用,元;Gn为第n年的设备发电量,MW;N为年数。
考虑折现率时,LCOE的表达式为
(14)
式中:rLCOE为考虑折现率时的LCOE,元;r为折现率。
2.2 目标函数
本文调度优化以系统购能成本CB、CLCOE、碳排放成本CC以及弃风弃光成本CWP之和C最小为目标函数,其数学表达式为
minC=CB+CLCOE+CC+CWP
(15)
系统购能成本CB主要包括外购电力成本、风光储的上网成本,以及火电上网成本,其表达式为
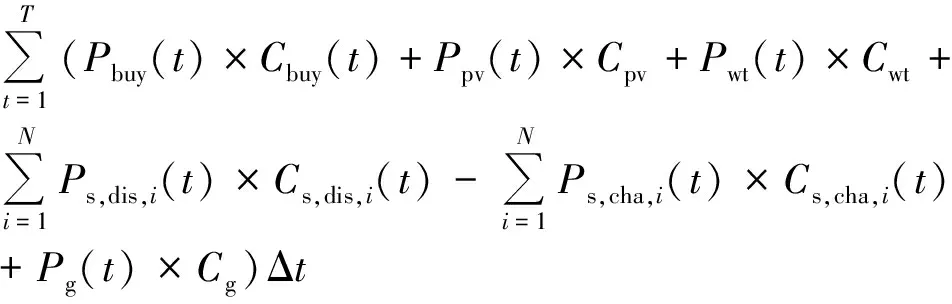
(16)
式中:Pg(t)为t时刻燃煤机组出力,MW;Cbuy(t)、Cpv、Cwt、Cs,dis,i(t)、Cs,cha,i(t)和Cg分别为t时刻系统购电价格、光伏上网电价、风电上网电价、储能上网电价、储能充电电价以及燃煤机组上网电价,元/(kW·h)。
LCOE包括火电、风电、光伏以及储能的单位标准度电成本之和,其表达式为

(17)
碳排放成本主要包括系统外购电力碳排放成本和燃煤机组碳排放成本。阶梯式碳交易下的碳排放计算公式参考式(11);传统碳交易下的碳排放的计算公式参考式(12)。
弃风弃光成本主要为风能及光伏所产生的电能不能被完全利用的部分,其成本公式为

(18)
式中:a为风光惩罚系数,元/(kW·h);Ppv,max(t)为t时刻光伏最大出力,MW;Pwt,max(t)为t时刻风能最大出力,MW。
2.3 约束条件
燃煤电厂发电功率约束为
0.3Pg,max≤Pg(t)≤0.8Pg,max
(19)
式中:Pg,max为火电机组额定出力,MW。
光伏发电出力约束为
0≤Ppv(t)≤Ppv,max(t)
(20)
风力发电出力约束为
0≤Pwt(t)≤Pwt,max(t)
(21)
抽水蓄能系统约束为
应该说,“首都餐饮业品质提升工作”是北京市餐饮业以习近平总书记关于食品安全系列讲话精神为指导,全面实施国家市场监管总局提出的《餐饮服务食品安全操作规范》的自律表现,是继北京餐饮业实现“明厨亮灶”、“阳光餐饮”后的一次全面提升,是为迎接2022年冬奥会打造餐饮业的首都标准、北京品牌,使北京餐饮业成为彰显首都文化魅力、良好生态环境、和谐文明社会、安定富裕生活的载体,成为体现首都城市内在品质的亮丽名片,在全国餐饮行业中做出了表率。下一步,中国烹饪协会将在北京市市场监督管理局的指导下,继续深入落实“首都餐饮业品质提升工作”,力争取得更大的成效,惠及更多的企业和消费者。
(22)
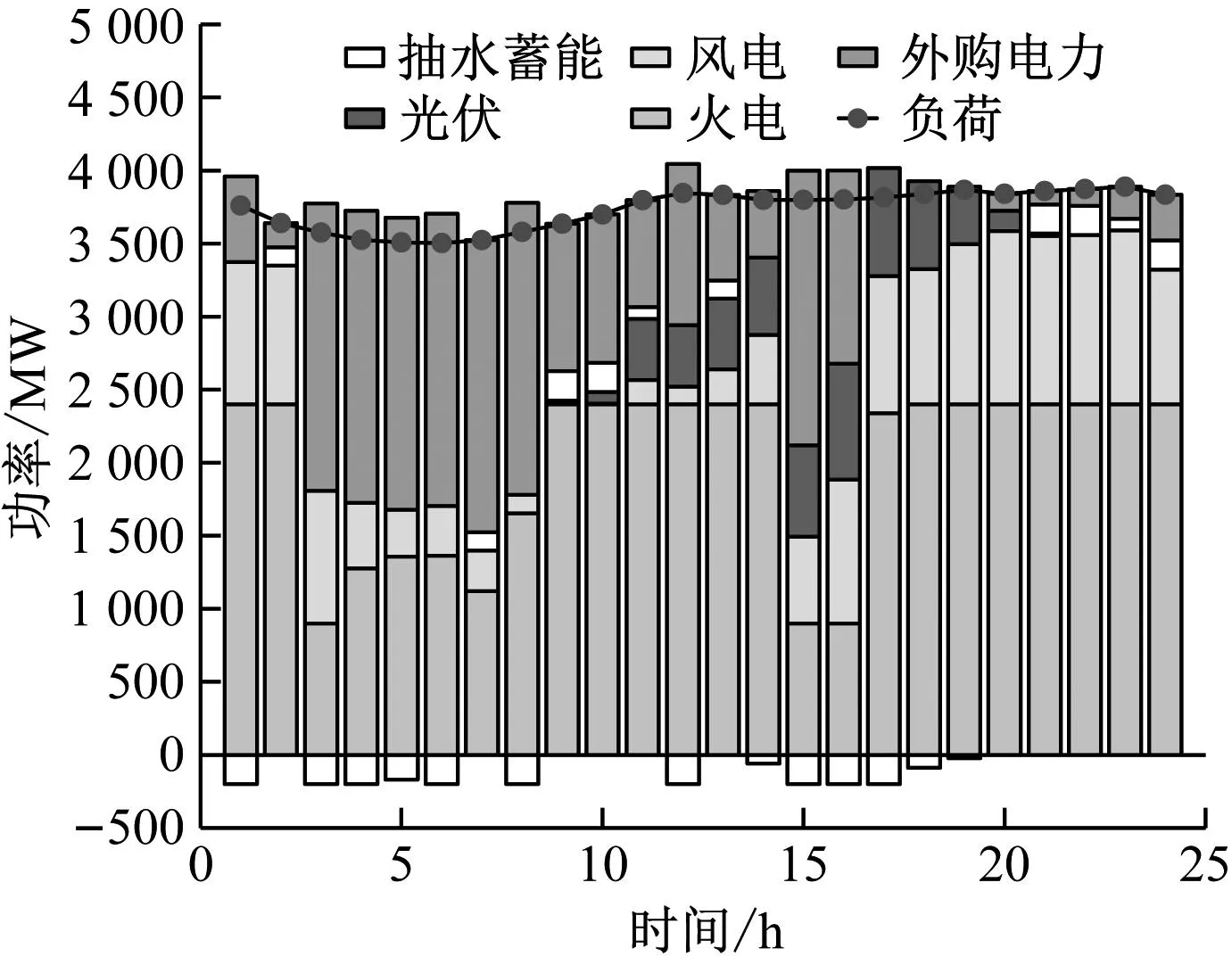
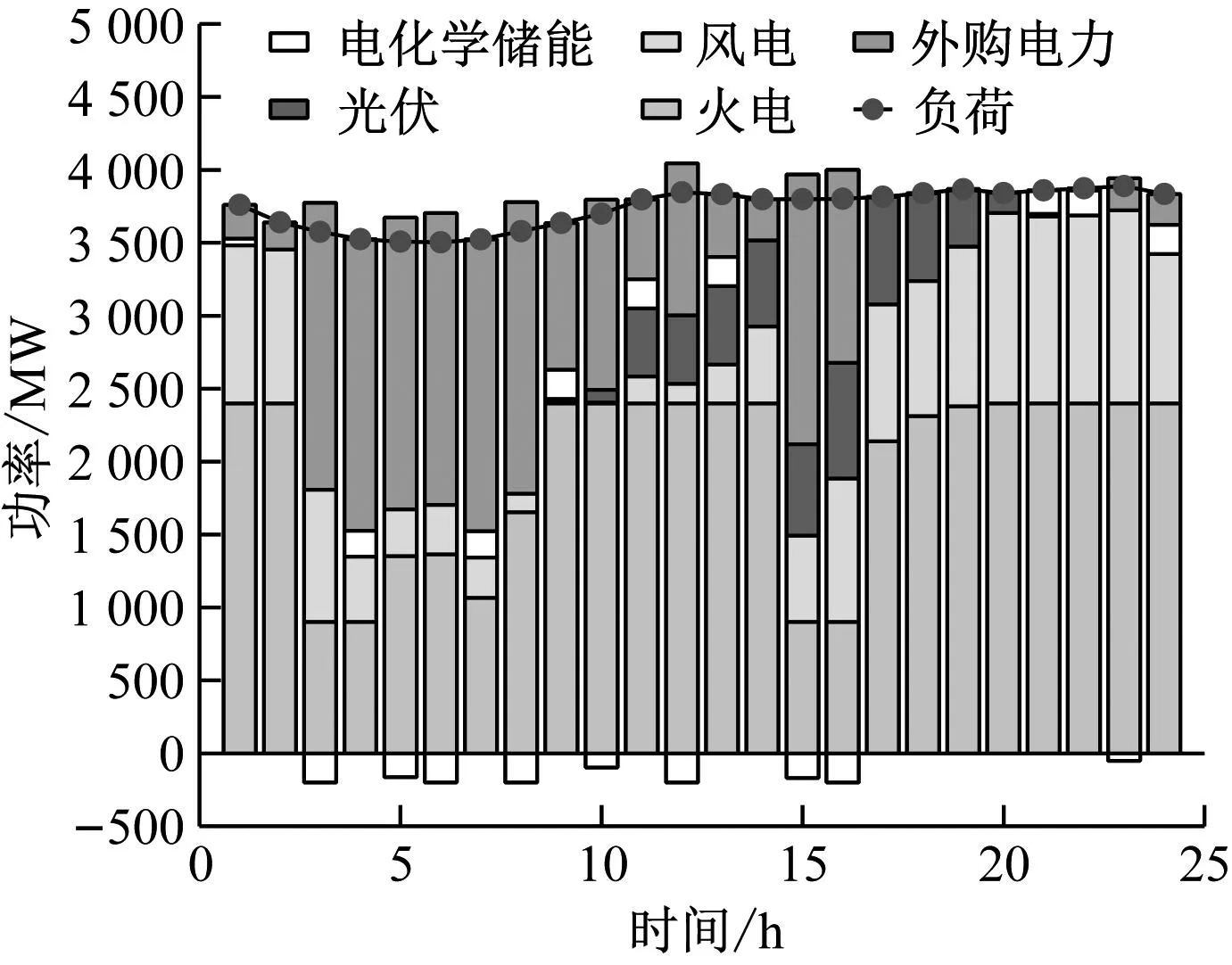
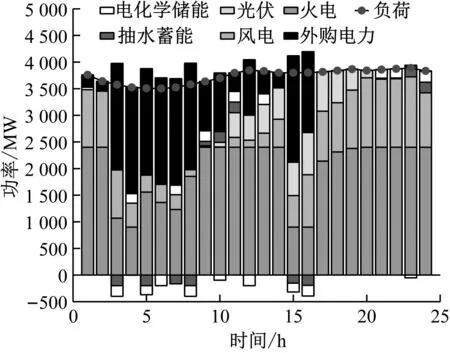
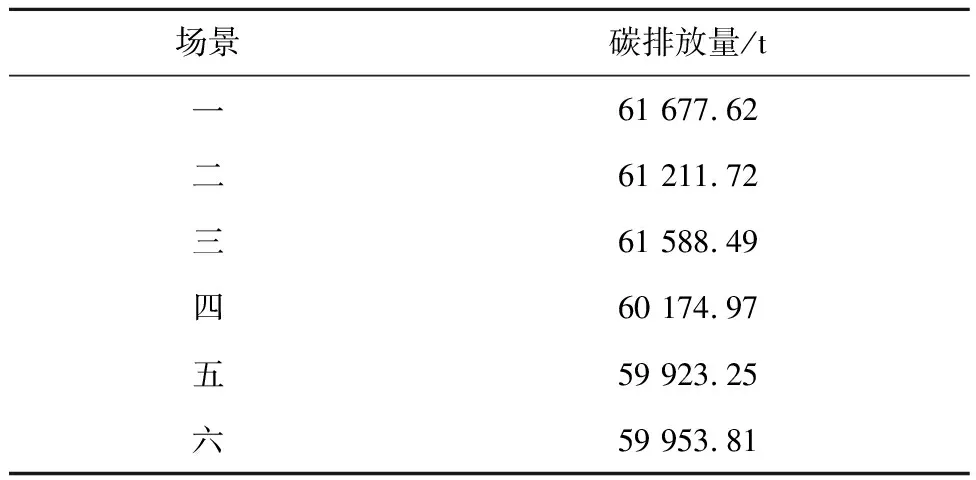
Pp,min (23) 式中:Et为上水库初始能量,MW·h;Emin为上水库最小能量,MW·h;ηh为发电转化效率;Ph(t)为t时刻抽水蓄能系统发电功率,MW;Ph,min为抽水蓄能系统发电功率最小值,MW;Ph,max为抽水蓄能发电功率最大值,MW;Pp(t)为t时刻水泵抽水功率,MW;Pp,min为水泵抽水功率最小值,MW;Pp,max为水泵抽水功率最大值,MW。 Eu,min (24) Ed,min (25) 式中:Eu为上水库储存能量,MW·h;Eu,min为上水库储存能量最小值,MW·h;Eu,max为上水库储存能量最大值,MW·h;Ed为下水库储存能量,MW·h;Ed,min为下水库储存能量最小值,MW·h;Ed,max为下水库储存能量最大值,MW·h。 电化学储能系统约束为 Pcha,min≤Pcha(t)≤Pcha,max (26) Pdis,min≤Pdis(t)≤Pdis,max (27) 式中:Pcha,max、Pcha,min分别为储能电池充电功率上、下限,MW;Pdis,max、Pdis,min分别为储能电池放电功率上、下限,MW;Pcha(t)、Pdis(t)分别为t时刻储能电池充放电功率,MW。 考虑到储能系统的寿命问题,在储能系统的充放电过程中,储能系统的电池荷电状态(SOC)不能超过设定的上下限,即 RS,min≤RSOC≤RS,max (28) 式中:RS,min为最小荷电状态,取0.2;RS,max为最大荷电状态,取0.9;RSOC为储能系统的电池SOC。 系统外购电力约束为 0≤Pbuy(t)≤Pbuy,max (29) 式中:Pbuy,max为系统最大外购电量,MW。 功率平衡约束为 (30) 式中:Pload(t)为t时刻系统负荷,MW。 采用MATLAB Yalmip工具箱的Cplex优化求解器进行优化调度求解。选取24 h为1个周期,电力负荷及风光出力数据参考我国西北某区域电网夏季典型日的实际数据。其中,火电装机3 000 MW、风电装机1 500 MW、光伏装机1 000 MW、抽水蓄能装机1 000 MW,电化学储能的功率/容量为200 MW/500 MW·h。根据2021年、2022年度全国碳排放权交易配额总量设定与分配实施方案,各参数取值为:Be=0.815 9,Fr=0.934,F1=1,Ff=1.087,Bh=0.110 4,ηe=0.728,βe=0.8,βs=1.08,c=0.25,α=0.25,d=5 000,a=0.3。该区域的电力负荷及风光出力数据如图1所示。 图1 负荷出力曲线 系统外购电力价格按照当地夏季分时电价并且执行尖峰电价机制,分时电价曲线如图2所示。火电上网电价为0.25元/(kW·h),风光上网电价为0.262元/(kW·h)。电化学储能充放电价按照分时电价执行,根据最新的储能政策,补贴设置为:弃风弃光段(00:00:00—05:00:00、13:00:00—18:00:00)充电补贴0.55元/(kW·h),放电补贴0.25元/(kW·h);平段充放电均为0.2元/(kW·h)。抽水蓄能上网电价与燃煤机组上网电价相等,抽水电价为燃煤机组上网电价的75%。考虑折现率及机组寿命,计算得出各类型能源的LCOE为:燃煤机组的单位度电成本为0.15元/(kW·h)、光伏机组的单位度电成本为0.18元/(kW·h)、风电机组的单位度电成本为0.16元/(kW·h)、抽水蓄能系统的单位度电成本为0.25元/(kW·h)、电化学储能系统的单位度电成本为0.65元/(kW·h)。 图2 夏季电网分时电价 为比较不同碳交易机制不同储能参与下的系统优化调度情况以及碳排放情况,提出6种场景,具体场景情况见表1。 表1 场景设置 按照所构建的6种场景及所给定的参数,以系统总成本最小为目标,进行调度优化计算,得出的优化调度结果如图3~图8所示。 图3 场景一 图4 场景二 图5 场景三 图6 场景四 图7 场景五 图8 场景六 不同场景下的碳排放情况见表2。比较不同碳交易机制下的碳排放情况,场景四相较于场景一,碳排放量减少1 502.65 t;场景五相较于场景二,碳排放量减少1 288.47 t;场景六相较于场景三,碳排放量减少1 634.68 t。可以看出,阶梯式碳交易机制下,其碳排放量小于传统碳交易机制下的碳排放量,证明了阶梯式碳交易的优势。比较不同储能配置方法调度优化后的碳排放情况,可以看出抽水蓄能与电化学储能协同调度下的碳排放量低于抽水蓄能和电化学储能单独调度下的碳排放量,证明了电化学储能与抽水蓄能协同调度下参与碳市场的可行性。 表2 不同场景下的碳排放情况 为验证不同碳交易机制下不同储能配置方式的经济效益优势,计算其电力市场以及碳市场的收益情况,结果汇总于表3。其中,电力市场收益的计算公式为:负荷×分时电价-购能成本-LCOE。由于本系统新能源比例较高,因此最终的碳排放配额高于实际碳排放量,二者之差即为可以进行售卖的碳配额量,其收益计算公式参考式(11)和式(12)。 由表3可以得出,传统碳市场交易机制下的售碳收益低于阶梯式碳市场交易机制下的售碳收益,这将更有利于鼓励高碳排企业进行低碳转型,从而售卖多余碳排放配额获得更高收益;抽水蓄能与电化学储能协同调度下的电力市场收益和碳市场收益均高于抽水蓄能和电化学储能单独调度下的电力市场收益和碳市场收益,进一步证明了阶梯式碳交易机制下电化学储能与抽水蓄能协同调度下参与电力市场及碳市场的可行性。 (1) 各时段各类型能源的配置情况为:抽水蓄能主要通过谷时蓄能、峰时放能来实现对电网的调峰,并且获得收益;电化学储能主要通过峰谷分时电价实现高低电价间套利,以及通过容量成本回收机制获得补偿收益。二者协同发展的经营模式,有利于维护电网的稳定,并且提高系统整体收益。 (2) 传统碳排放机制下,系统的整体碳减排积极性难以调动,引入阶梯式碳交易机制后,系统的碳减排积极性有明显的提高。传统碳市场交易机制下的售碳收益低于阶梯式碳市场交易机制下的售碳收益,这将更有利于鼓励高碳排企业进行低碳转型。 (3) 抽水蓄能与电化学储能协同调度优化下的碳排放量低于抽水蓄能和电化学储能单独调度下的碳排放量,证明了抽水蓄能与电化学储能协同调度下参与碳市场的可行性;抽水蓄能与电化学储能协同调度下的电力市场收益高于抽水蓄能和电化学储能单独调度下的电力市场收益,证明了电化学储能与抽水蓄能协同调度下参与电力市场的可行性。所提出的电化学储能与抽水蓄能协同参与电力市场与碳市场的配置方案,验证了电化学储能与抽水蓄能同时接入电网后进行系统调度优化的可行性。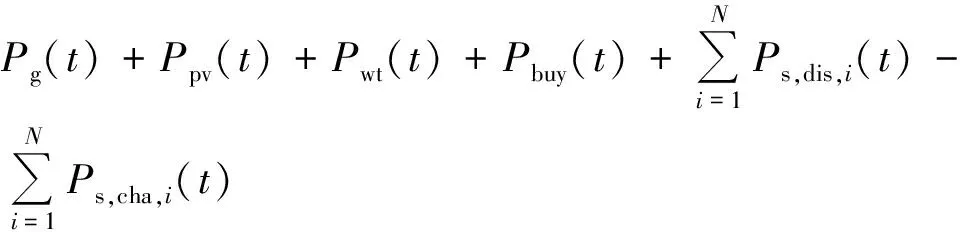
3 算例分析






4 结论

