基于改进等效电路模型的直流微电网大信号稳定性分析

王 力 谭振杰 曾祥君 赵 斌 郑月球

基于改进等效电路模型的直流微电网大信号稳定性分析

王 力1谭振杰1曾祥君1赵 斌1郑月球2

（1. 长沙理工大学电气与信息工程学院 长沙 410114 2. 西藏华东水电设备成套有限公司 拉萨 851414）

对高阶非线性直流微电网进行简化建模是大信号稳定性分析的有效方法。传统简化模型主要关注LC滤波器和线路阻抗等参数，难以分析换流器控制参数的影响，所建立的判据存在难以准确反映直流微电网稳定域的问题。因此，该文提出直流电压下垂控制换流器的具备完整状态变量集的改进等效电路模型，相比于传统简化模型，能更准确地刻画系统低频响应特性。基于混合势理论推导了直流微电网大信号稳定判据及其稳定域，并结合LaSalle不变集定理得到能量指标，以反映系统稳定性变化趋势。建立的稳定判据可指导控制参数优化，且能拓展到多端直流微电网的大信号稳定性分析。在多场景下仿真验证了所提改进等效电路模型和大信号稳定判据的有效性。

直流微电网 大信号稳定性 等效模型 直流电压控制 混合势理论

0 引言

为切实落实我国“碳达峰、碳中和”的发展目标，高比例可再生能源及高占比电力电子化负荷是电力系统发展的特点[1-2]。直流微电网作为整合可再生能源的有效解决方案已广泛应用于可再生能源发电系统、电动汽车、电动船舶等领域[3-4]。但直流电网中可再生能源的强波动性及恒功率负载（Constant Power Load, CPL）的负阻特性等因素给稳定运行带来的不利影响仍难以解决[5-6]。此外，直流系统的-耦合特性和惯量小的特点使得较小的电源或负荷变化也可能导致电压闪烁或振荡[7-8]。

针对直流电网中的不稳定现象，国内外学者在小信号分析方面已开展了大量研究[9-12]。如文献[11]根据换流器的等效输出阻抗分析了控制参数对直流母线电压动态性能的影响；文献[12]建立了多电压等级直流配电系统的小信号模型，并推导了基于系统等效环路增益的系统小信号稳定判据；文献[13]基于变流器输出阻抗研究了下垂控制变流器并联系统的振荡机理。然而小信号研究往往只适用于分析直流系统小信号扰动的情况，不适用于大信号扰动下的稳定性分析[14-15]。

直流微电网呈现高阶非线性特点，建立其详细模型进行大信号稳定性分析会带来庞大的计算量，可能造成维数灾难[16-17]。故现有直流微电网大信号研究中往往基于低频降阶模型来构造李雅普诺夫函数[17]，并采用Takagi-Sugeno模型法[18]、Lyapunov直接法[19]、Hamilton曲面成形法[20]、混合势理论[17,21-22]等直流微电网大信号分析方法得到直流微电网大信号稳定判据和确定渐近稳定域[23-24]。如文献[17-18]分别应用混合势理论和Takagi-Sugeno模型法进行了直流微电网集群的稳定性分析；文献[19]针对多源并联系统推导了基于Lyapunov直接法的大信号稳定判据；文献[20]提出了基于Hamilton曲面成形法的大信号亚稳态分析法，对非线性时变负载脉冲产生的非线性极限环进行了稳定性评估。上述基于Takagi-Sugeno模型法、Lyapunov直接法和Hamilton曲面成形法的研究将电压源换流器建立为由电压源、下垂虚拟电阻、LC滤波器及其寄生电阻构成的二阶模型，难以进一步分析换流器控制器参数的影响[18-20]。目前大信号稳定判据存在一定的保守性问题[25-26]，如何建立兼顾准确度和计算速度的通用非线性降阶模型，是分析直流系统暂态稳定性问题的关键[27]。

在直流微电网稳定性分析方面，应用混合势理论可提供包含控制器参数、滤波器参数和线路阻抗的大信号稳定判据[26]。其中，文献[22,28]将换流器等效为受控电流源，根据混合势理论分别研究了多个下垂控制换流器的不同功率分配比例和电压环存在输出限幅等条件对直流微电网大信号稳定性的影响。然而，目前基于混合势理论的直流微电网稳定性分析仍受困于建模方法不够合理，使得分析过程丢失了控制系统中积分环节的参数信息。针对一种采用新型下垂控制器的直流微电网，可借助混合势理论通过其等效电路模型实现对下垂控制器参数的分析[29]。对电压环PI控制参数进行优化设计后能增强系统阻尼，提高直流系统暂态稳定性[6]。但因基于传统简化模型所得到的大信号稳定判据难以涵盖电压环控制参数，在多换流器情况下通过优化设计这些参数来提高系统大信号稳定性仍存在困难。

综上所述，为解决大信号稳定判据因简化建模忽略某些关键控制参数，导致判据难以准确反映直流微电网稳定域的问题，本文针对采用直流电压下垂控制的换流器，提出一种改进的等效电路模型，在考虑CPL的非线性特征后建立直流微电网的等效非线性电路模型。应用混合势理论对等效非线性电路模型进行分析，推导直流微电网的大信号稳定判据，进而计算得到系统大信号稳定的参数域和功率运行范围，并结合LaSalle不变集定理得到能量指标，以反映系统稳定性变化趋势。仿真验证了所提出建模方法的有效性及得到的稳定判据的正确性。

1 直流微电网及其简化模型

1.1 换流器控制系统及其等效电路模型

1.1.1 通用电压源换流器控制系统

直流微电网的典型架构如图1a所示，其中包括分布式发电系统（Distributed Generation System, DGS）、负载和电池储能系统（Battery Energy Storage System, BESS），也可包含交流电网的互联换流器。图1b为直流微电网的基本形式，包括源换流器、负载换流器和直流母线。

研究图1b所示的级联换流器系统的稳定性可作为研究直流微电网整体稳定性的前提[30]。在不失一般性的情况下，本文以图2所示通用源荷双端直流微电网为基础，建立其等效电路模型，研究系统参数对直流微电网稳定性的影响。

图1 典型直流微电网结构

图2 通用源荷双端直流微电网及其控制系统

图2所示源换流器为AC-DC换流器或DC-DC换流器，采用由-下垂控制、直流电压控制和内环电流控制组成的典型控制结构，实现为负载供电和电压调节，其中AC-DC换流器无功电流参考值qref为0。负载由CPL和并联阻性负载组成。图2中，ref和o分别为换流器输出电流的设定值和实际值；sref为内环电流控制参考电流；dcset、dc和bus分别为直流电压设定值、换流器输出电压和直流母线电压；line为线路电流；d为下垂系数；f为换流器的滤波电容；line和line为直流线路阻抗；L和L分别为负载侧电容和并联阻性负载等效电阻。

直流电压控制结构中，换流器实际输出电压dc通过PI控制器udc()跟踪输出电压参考值，其中输出电压参考值由直流电压设定值dcset和下垂控制输出相加得出。udc()可写成

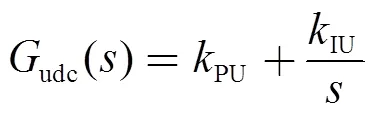
式中，PU和IU分别为直流电压控制的比例系数和积分系数。

当ref=0时，换流器输出电压动态方程可表达为[31-32]

式中，dcset=dcset+Δdcset；o=o+Δo；line=line+Δline；dcset、o和line分别为直流电压设定值、换流器输出电流和线路电流的稳态值；Δdcset、Δo和Δline分别为相应电压电流的扰动量；in()为内环电流控制的闭环传递函数；为电流转换系数，对于AC-DC换流器，=1.5d0/dc0，其中d0为交流侧电压在park变换下的d轴分量稳态值，dc0为直流电压稳态值，对于DC-DC换流器，=1。式（2）所示的单个换流器的直流侧输出电压动态方程为进一步得到系统的等效电路模型奠定了基础。

1.1.2 电压源换流器的改进等效电路模型

在直流系统的大信号分析中，传统的建模方法通常分为两种，其一为将换流器建立为包含电压源、下垂虚拟电阻和LC滤波器的二阶模型[17-20]，然而仅考虑这些参数难以准确地描述换流器控制系统的响应特性；其二为将换流器建立为受控电流源模型，但这类方法在求解过程中会丢失部分控制参数信息[21-22,26,28]。由于电压源型换流器可根据基本的RLC电路等效模拟，适用于分析换流器的暂态过程和静态特性[33]，故本文基于平均值模型构造等效电路描述系统的低频响应特性，并分析系统的稳定性。

通常电压源换流器中直流电压控制链路的响应时间常数约10倍之于电流控制，为便于研究换流器的低频响应特性和多换流器并联系统的稳定性，可忽略快速电流控制的影响[34]，则化简式（2）可得

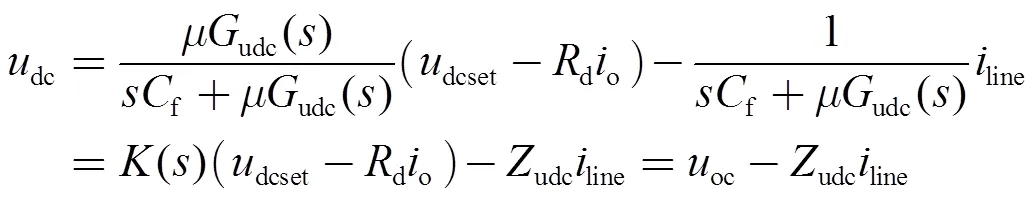
式中，()为仅滤除高频分量的二阶滤波器，当滤波电容f取值较小时可认为()=1；oc和udc分别为换流器等效电路模型的开路电压和输出阻抗。

根据戴维南定理，由式（3）可得到换流器等效电路的基本模型如图3a所示。下垂系数d可看作电压源内阻，换流器输出阻抗udc可表达为

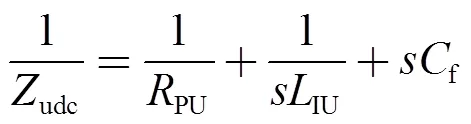
其中

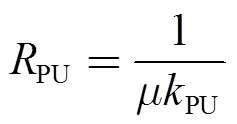
图3 单个电压源换流器的等效电路模型

针对非线性系统，混合势理论提供了简单有效的Lyapunov类型函数构造方法及稳定定理，常应用于分析直流电网的稳定性。鉴于混合势理论对具有完整状态变量集（即变量集合{1,2,…,,+1,+2,…,+n}是完整的，其中1,2,…,为通过电感的电流，+1,+2,…,+n为电容的电压）的电路有完善的分析方法，而对非完整电路则难以构建起标准混合势函数[35]。故本文对换流器的输出阻抗模型进行了改进，改进后的模型如图3b所示，并且满足关系

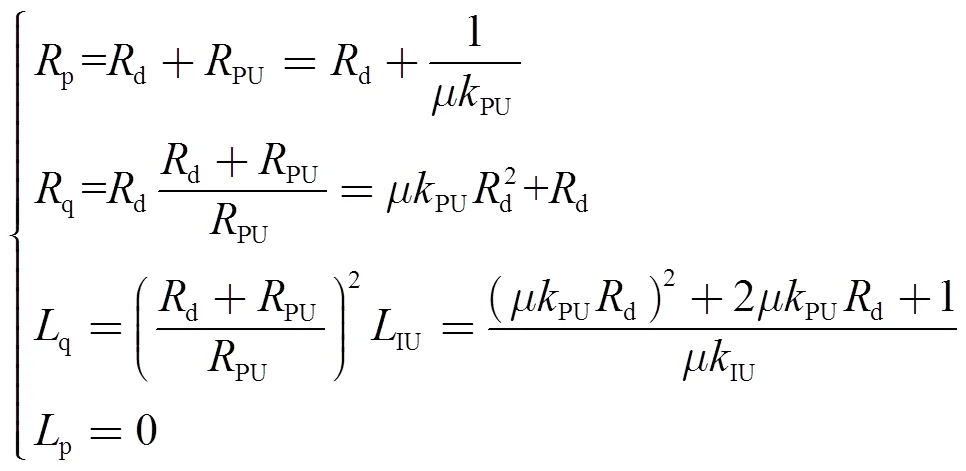
式中，p为构造的虚拟电感，其值无限趋于0。则改进的等效电路模型仍可看作二阶模型。

图3b的模型通过p和q两个并联支路替代了图3a中的下垂系数等效阻抗和电压PI控制器的等效阻抗，建立了状态变量集完整的电路模型。

1.2 直流微电网的等效非线性电路模型

根据换流器的改进等效电路模型，建立源荷直流微电网的等效非线性电路模型，如图4所示。图中，CPL为CPL功率，CPL为CPL的电流。所考虑的非线性CPL满足式（6），其外特性曲线如图5所示。

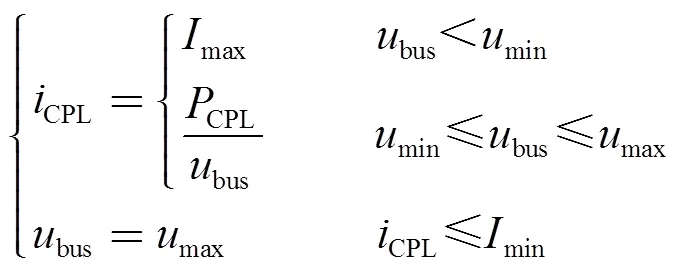
式中，umax和umin分别为负载电压的上限和下限；Imax和Imin分别为CPL电流的上限和下限。本文主要关注一般运行状态，即umin≤ubus≤umax的情况，此时CPL消耗功率的特性使其表现出正阻特性，而恒定功率控制使其受到扰动时对外表现出负阻特性。

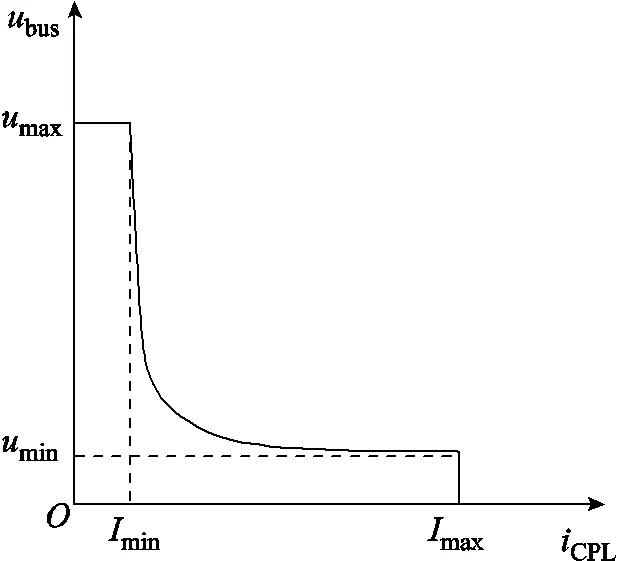
图5 CPL外特性曲线

通过上述过程，本文提出了一种直流电压下垂控制换流器的改进等效电路模型，结合CPL和并联阻性负载后得到了具有完整状态变量集的等效非线性电路模型，降低了数学模型中状态变量的耦合程度，达到了降低模型求解难度的目的。

2 直流微电网大信号稳定性分析

2.1 直流微电网的混合势函数及其大信号稳定性判据

基于Brayton-Moser的混合势理论，对于图4中的模型可得到动态方程

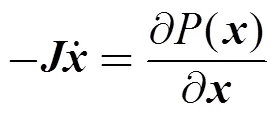
其中

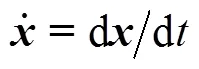
式中，和分别为对角电感矩阵和对角电容矩阵；()为混合势函数，被定义为描述系统电压势能和电流势能的标量函数，其一般形式可以表示为

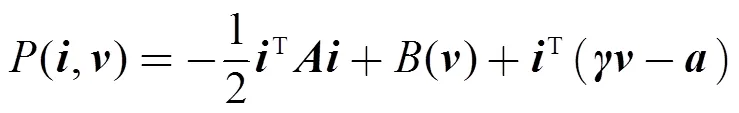
图4所示模型的混合势函数可构建为

式中，积分范围为被积变量的最小值到稳态值，下文皆同。

对式（7）求解得到混合势函数()与时间的关系为

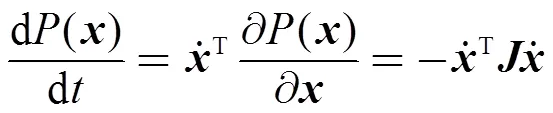
由于是否为正定取决于和的值，故构造矩阵和函数()来进一步分析系统稳定性。和()表达式为

根据Brayton-Moser混合势理论定理3[35]，若为正定矩阵，满足当||→∞时()+||→∞，并且对于所有、有

根据式（9）得到式（8）中相关矩阵为

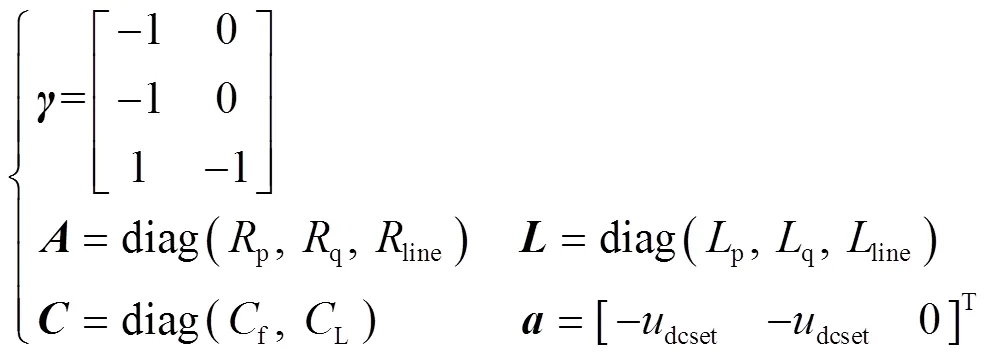
结合式（5）、式（12）和式（13），得到直流微电网大信号稳定判据为

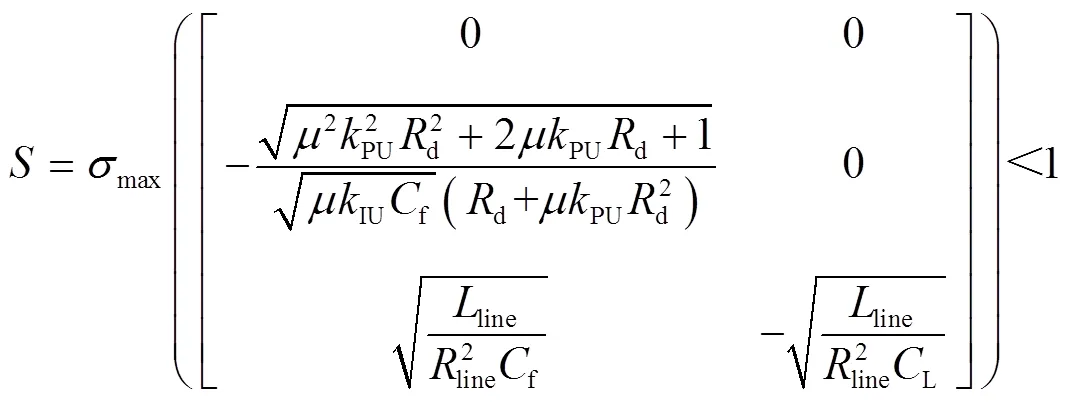
式中，max()为计算最大奇异值；为最大奇异值，可根据直流微电网的参数计算得到。

式（14）可保证系统遇到大扰动时能够收敛到平衡点集，然而不能直接确定每个平衡点的稳定性。具体而言，对于所考虑的非线性CPL，负阻特性下的平衡点稳定性仍不确定[19]。可通过式（15）对平衡点的稳定性进行考察，进一步缩小不变集。

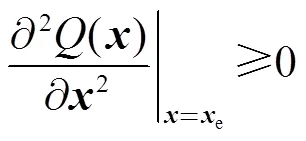
式中，e代表系统的平衡状态。

求解式（15）得到

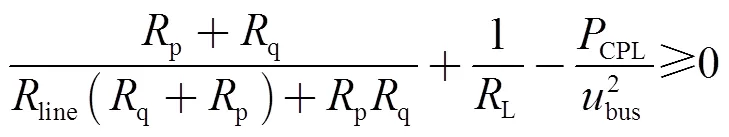
当系统处于稳态时，p支路和q支路的阻抗存在关系1/p+1/q=1/d，由此可得到

式中，为系统总导纳。

由上述分析可知，当满足式（14）和式（17）时，d()/d＜0成立，但()的正定性仍不确定。鉴于LaSalle不变集定理并不要求()正定，故应用该定理对系统状态进行分析。LaSalle不变集定理介绍如下[36]。

对于条件①，由于系统满足当||→∞时()→∞[35]，由式（11）可知，系统的平衡点（d/d0）正是()的驻点，即∂()/∂=0，且电路系统中平衡点的数量是有限的，所以是一个紧集。对于条件②，式（14）已对系统进行约束，故可通过()表征系统能量，根据系统运行时d()/d的变化趋势辅助判断基于等效电路模型的稳定性分析结果与系统运行结果是否具有一致性。

由式（14）和式（17）得到了系统大信号稳定的两个条件，其中前者保证发生扰动时系统状态变量随时间的增大收敛到平衡点集，后者则保证了平衡点集内所有平衡点是稳定的，用以计算系统的功率运行范围。

2.2 系统参数对直流微电网稳定性的影响

2.2.1 系统大信号稳定的参数域

根据式（14）对系统参数进行分析，研究系统能量随时间的增大而趋于稳定的参数域。以PU=0.1、IU=120、d=0.541、f=56.5 mF、line=0.25 mH、line=0.5 Ω（即表2中第二组参数）为基准，改变各系统参数并计算最大奇异值得到三维曲面如图6所示。图中黑色曲线为系统参数的大信号稳定边界=1。

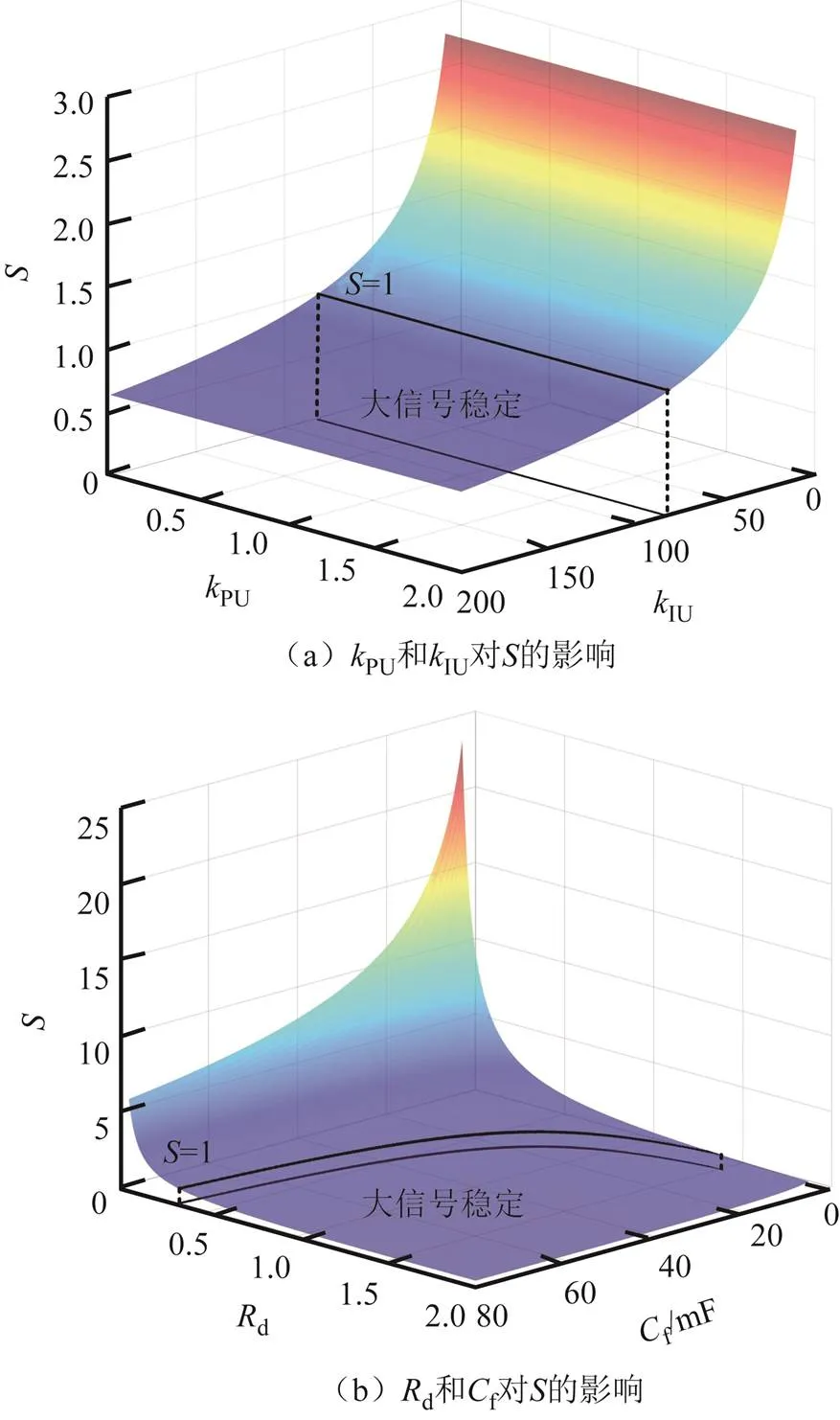
由图6可知，随着d、IU、f和line的增大，系统的最大奇异值减小，系统的大信号稳定性增强；而随着线路电感line增大，系统大信号稳定性减弱。由图6a可知，PU的变化对的影响较小，其原因在于PU主要影响p支路中p的大小，而p对系统振荡的影响较小。故由图6中各分图可知，增大电容、减小等效电感均有助于增强大信号稳定性。实际情况中，因受到多方面因素的影响，f和line不能任意整定，可通过增大电压环积分系数IU来减小q，为系统提供更多的稳定裕度。

2.2.2 系统恒功率负载稳定运行范围

建立系统稳态时的诺顿等效模型如图7所示。

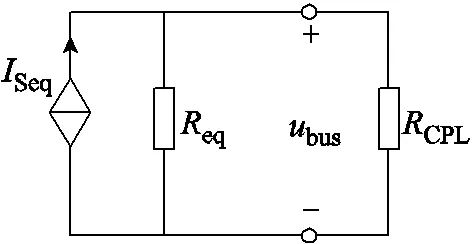
图7 直流微电网稳态时的诺顿等效模型

图7中，eq、Seq和CPL可分别表示为

其中，bus的稳态电压buse满足

式中，Le为CPL稳态电流。

当CPL功率值等于最大传输功率，且系统进入稳态时，若CPL呈现正阻特性，则其值与eq相等；若呈现负阻特性，则存在eq+CPL=0，与式（17）中=0等价。若CPL功率值继续增大，则存在eqCPL/(eq+CPL)＜0，即＜0，此时系统不存在稳定的平衡点。由此计算系统的恒功率负载稳定运行范围为

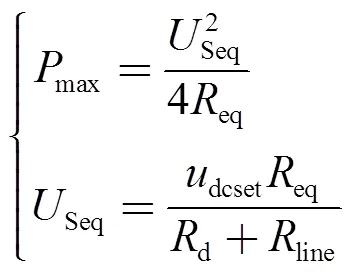
结合式（20），当系统满足式（14）且CPL＜max时处于恒稳定区域；而系统不满足式（14）时则处于大信号非稳定区域，此时应减小CPL的功率值。结合图6和式（20）可知，d和line的增大会令减小，从而提高系统稳定性，但同时也会减小max，降低系统的带负载能力，而且随着d和line的增大还会造成更大的母线电压降落，影响电能质量。因此，参数优化配置应结合系统稳定性、母线电压偏差和系统效率等多方面因素综合考量。

2.3 模型及判据的对比与分析

传统建模方法中大信号稳定判据存在保守性问题，采用混合势理论对三种建模方法的大信号稳定判据进行对比分析。为便于表述，模型一表示本文所提出的改进等效电路模型；模型二表示将换流器等效为电压源和LC滤波器的模型；模型三表示将换流器建立为受控电流源的模型。其中模型二和模型三如图8所示。

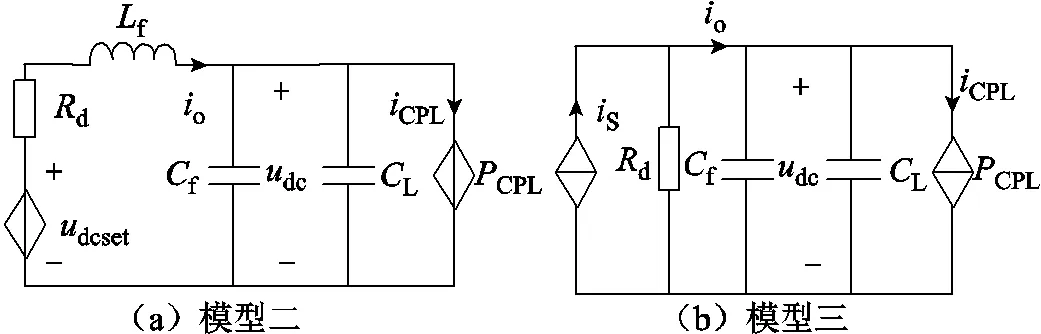
图8 不同建模方法下的直流微电网模型

2.3.1 模型一的大信号稳定判据

以图4所示的模型为基础，忽略线路阻抗和并联阻性负载后得到模型一的大信号稳定判据为

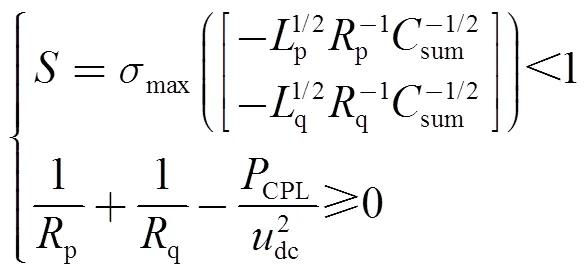
其中

计算式（21）可得到系统大信号稳定判据的解析表达式为

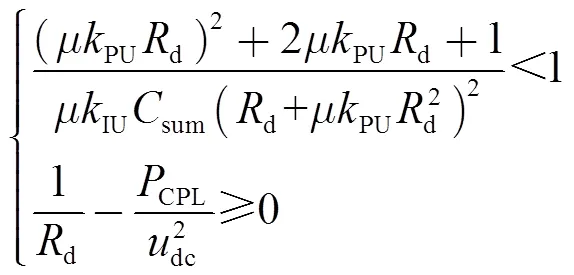
2.3.2 模型二的混合势函数及其判据

图8a为将换流器等效为电压源和LC滤波器模型的直流微电网模型[17-19]，即模型二，构造其混合势函数可得到

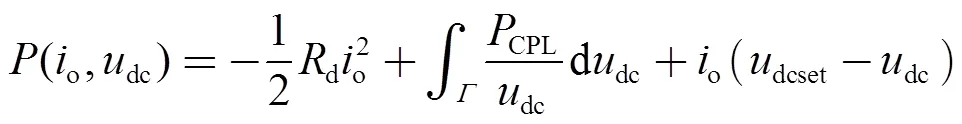
由式（23）定义(o)和(dc)，并计算其二阶导数得到

对于模型二，系统大信号稳定时应满足1+2≥0，则模型二的大信号稳定判据可表示为

2.3.3 模型三的混合势函数及其判据

图8b为将换流器等效为受控电流源的直流微电网模型[21-22]，即模型三。假设电流环的响应足够快，换流器输出电流S可及时跟踪参考值，则受控电流源S由电压环输出值得出，表示为

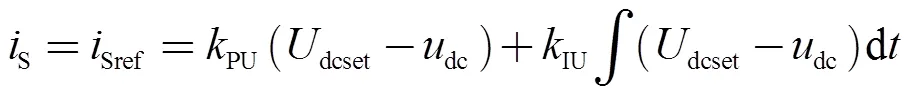
模型三中将下垂控制等效阻抗以受控电流源并联虚拟电阻的形式体现，构造图8b所示模型的混合势函数为

由此得到模型三混合势函数中不存在关于电感电流的项，故(dc)=(dc)，并计算其二阶导数为

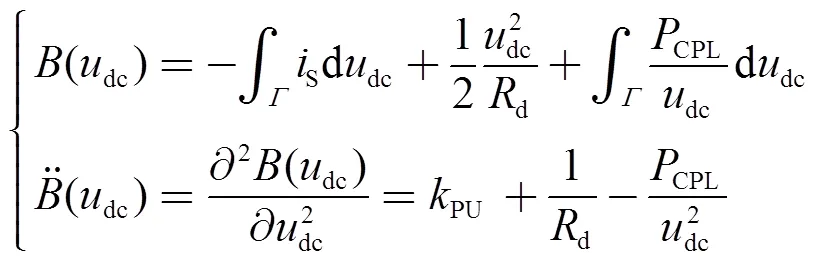
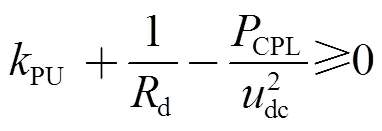
模型二的判据中考虑了下垂等效电阻、LC滤波器和恒功率负载的影响，然而电压环控制参数是影响系统响应的重要因素，导致可能难以实现对换流器控制系统稳定性的准确判断。模型三的判据中因电压环比例系数被当作受控电流源的内阻且难以分析电压环积分系数的影响，导致分析结果可能存在误差。

3 仿真验证

在Matlab/Simulink中建立图9所示的基于换流器开关模型的直流微电网模型用于仿真验证。直流微电网组成部分参数见表1。结合图6中系统大信号稳定的参数域分析结果，设计了四组直流微电网仿真参数用于进行大信号稳定判据验证，其中第一组和第三组参数不满足＜1，第二组和第四组参数满足＜1，并计算改进等效电路模型参数，见表2。

图9 基于换流器开关模型的直流微电网拓扑

表1 直流微电网组成部分参数

Tab.1 Parameters of each component of the DC microgrid

（续）

表2 四组直流微电网仿真参数

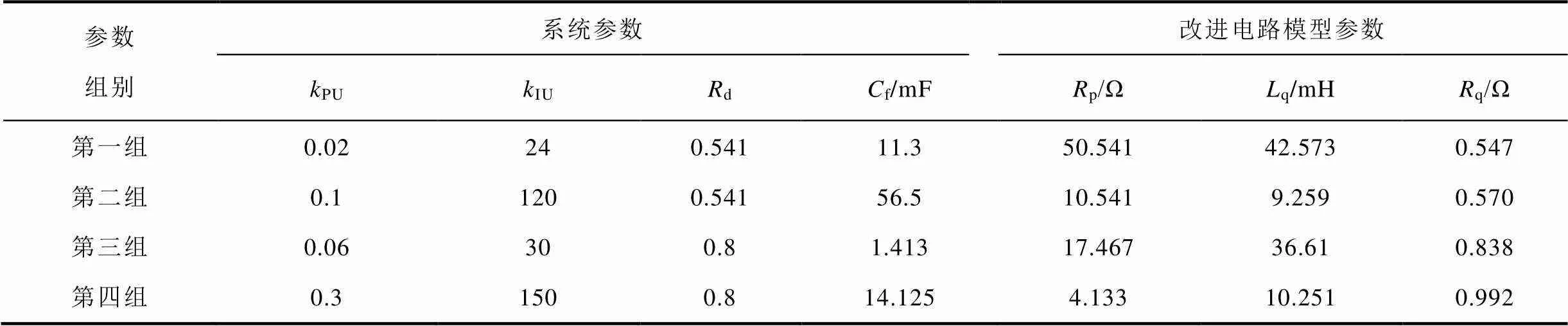
Tab.2 Four sets of DC microgrid simulation parameters

3.1 系统参数对直流微电网稳定性的影响

首先，为分析换流器参数对直流微电网大信号稳定性的影响，以表2中第一组参数为基础分别改变各换流器参数，进行功率扰动实验。2 s前系统已进入稳态，设定在2 s时CPL功率值由0阶跃至10.7 kW，得到直流电压响应波形如图10所示。

图10 换流器参数变化时的直流电压动态响应

由图10a和图10b可知，随着电压环比例系数PU和积分系数IU增大，系统响应加快，超调减小；由图10c可知，下垂系数越大，系统稳态时的电压降越大，同时系统的阻尼增大，响应速度增加；由图10d可知，随着滤波电容f增大，系统超调减小。

为分析线路阻抗对直流微电网大信号稳定性的影响，以表2中第一组参数为基础改变线路阻抗，进行功率扰动实验。2 s前系统已进入稳态，设定在2 s时CPL功率值由0阶跃至10.7 kW，得到直流母线电压响应波形如图11所示。

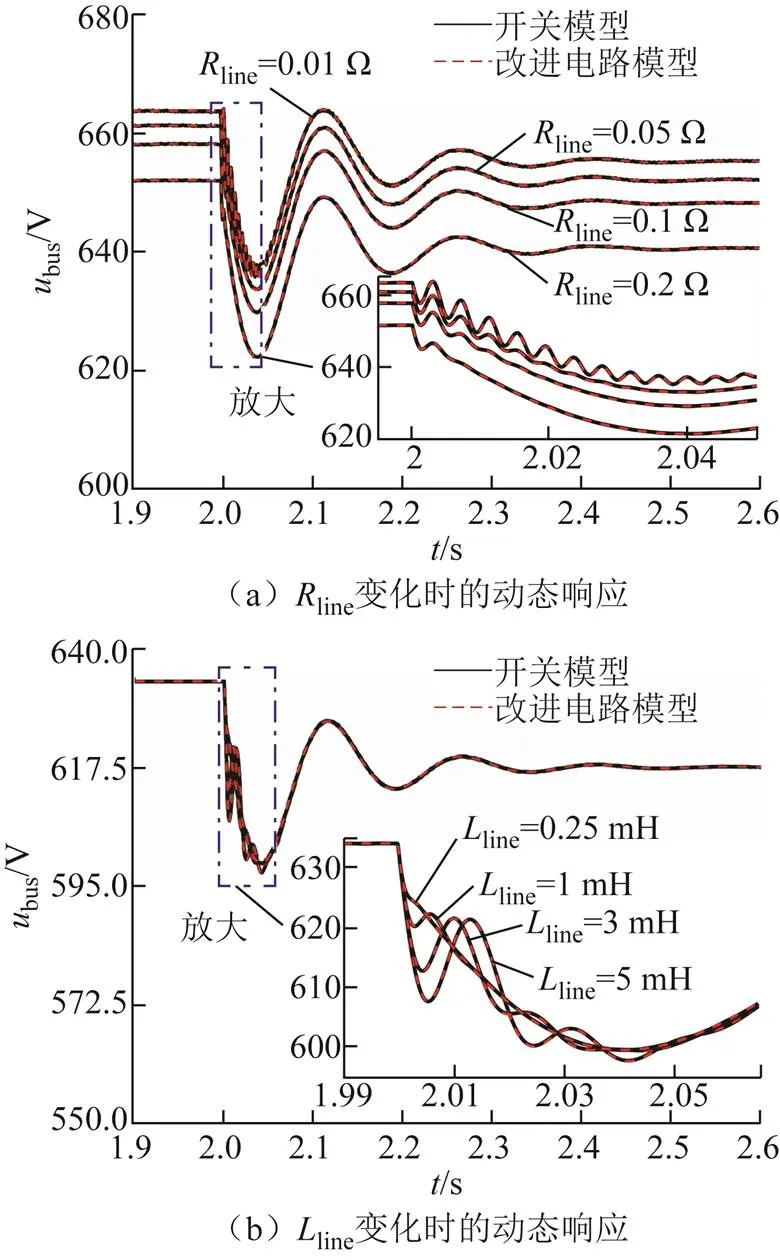
图11 线路阻抗变化时的直流母线电压动态响应

由图11a可知，随着线路电阻line的减小，恒功率负载发生阶跃后直流母线电压的振荡时间逐渐增加；由图11b可知，随着线路电感line的增加，恒功率负载发生阶跃后直流母线电压的振荡幅度增大。综合图10和图11各分图可知，各系统参数变化工况下，所提改进等效电路模型和直流微电网详细模型的直流电压动态响应一致，具有相似的暂态稳定性。

由式（11）可知，(,)函数值能表征系统能量变化。为探究不同参数设置下发生功率扰动后系统能量波动变化规律，根据上述改变换流器控制参数和线路阻抗参数进行功率扰动实验得到的系统运行数据绘制(,)函数值变化曲线，如图12所示。

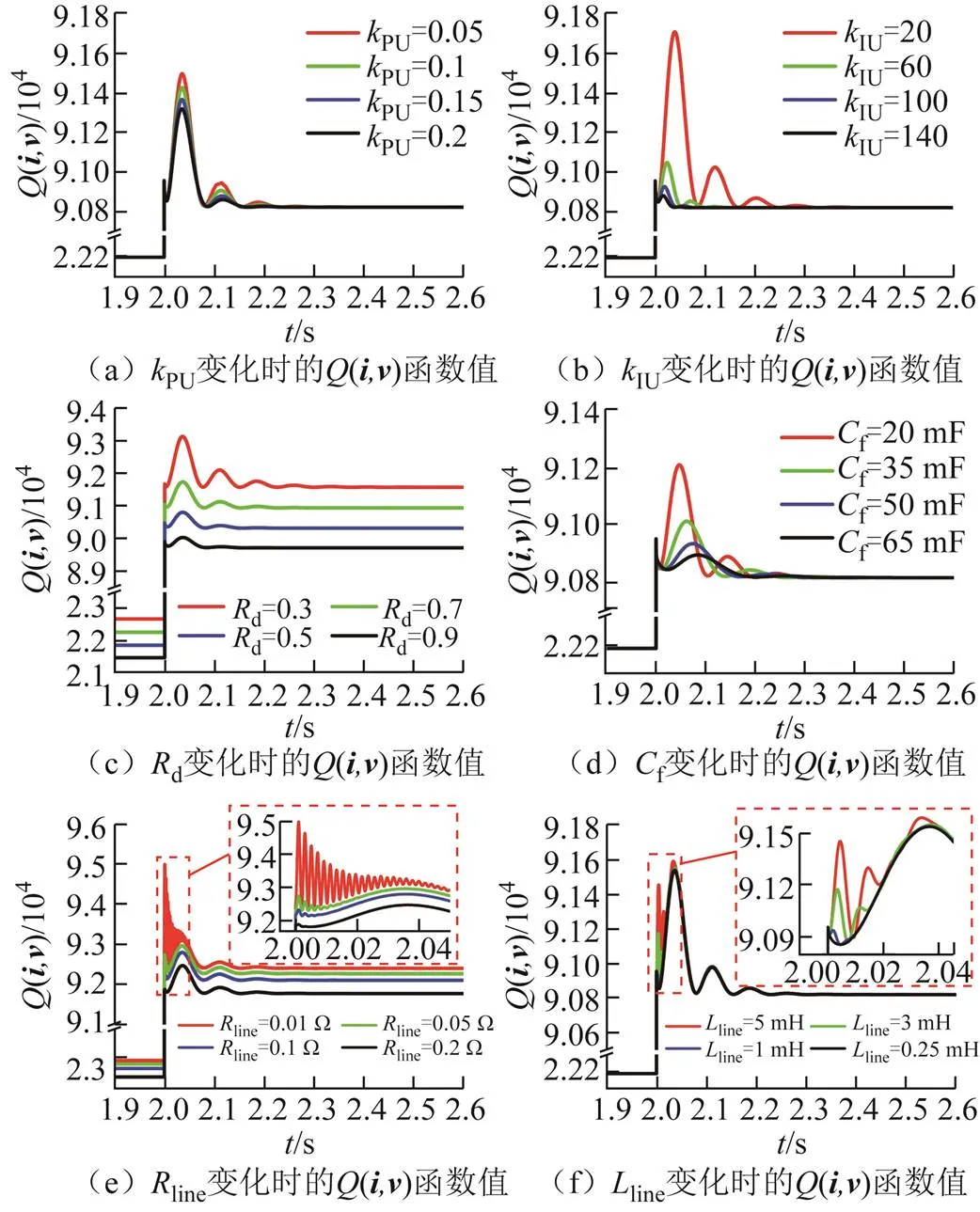
图12 不同参数下功率扰动时Q(i, v)函数值变化曲线

由图12各分图可知，在系统的稳态工作点e(e,e)处，(,)函数值最小。发生扰动后，随着时间增大，(,)函数值经过一系列波动后回到稳态值，表明系统能量逐渐趋于稳态。由图12a和图12b可知，PU的增大减小了能量波动的峰值，但基本未改变能量波动趋势，IU的增大则减小了能量波动的峰值和达到峰值的时间；由图12c可知，d的增大减小了能量波动的峰值和系统能量的稳态值；由图12d可知，f的增加使系统的惯量增大，能量波动减小；由图12e和图12f可知，line减小和line增大均将会加剧系统的能量波动，系统大信号稳定性降低，主要表现为负载接入瞬间产生的高频振荡。综合图10～图12可知，直流电压响应曲线和(,)函数值变化曲线具有相似的波动程度，可通过式（14）计算数值并结合(,)函数值变化规律对系统的稳定性进行判别。

3.2 大信号稳定判据验证

3.2.1 大扰动时系统的大信号稳定判别

除了分析系统参数对稳定性的影响趋势外，还需结合图6中系统大信号稳定的参数域边界，进一步研究大扰动场景下大信号稳定判据＜1与系统稳定性的关系。根据表2中四组参数构建了大扰动场景1～场景4，均设定在2 s时接入CPL。四种场景的大信号分析结果与仿真结果见表3。其中，根据式（20）计算max1=0.107 MW为第一组和第二组参数的功率边界，max2=0.083 MW为第三组和第四组参数的功率边界。以场景1和场景2为例进行详细分析，仿真结果如图13所示。

表3 大扰动场景下的对系统大信号稳定性的影响

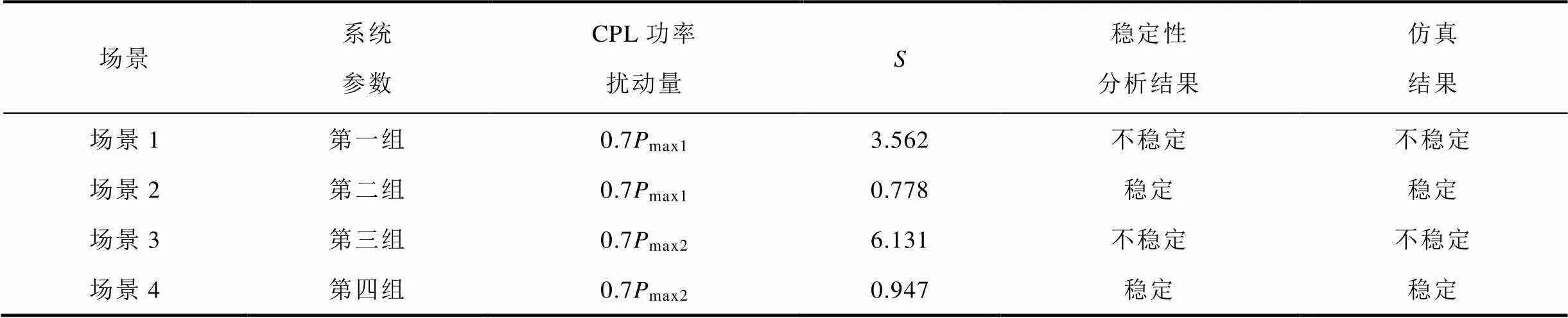
Tab.3 Influence of S on large-signal stability in large disturbance cases

图13 场景1和场景2下直流电压动态响应和Q(i, v)函数值变化曲线

由表3可知，场景1不满足＜1，故CPL发生扰动时，系统可能会失稳；场景2满足＜1和CPL＜max1，故系统将是大信号稳定的。结合图13a可知，场景1中CPL接入后直流电压发生等幅振荡，难以收敛到平衡点；图13b中(,)函数值跃变后继续表现出增长趋势，随后发生能量振荡的现象。由图13c和图13d可知，发生大扰动后，场景2的直流电压经过短暂电压调节快速达到了稳态，并且(,)函数值在CPL扰动后随时间增加而单调递减到稳态值。综合表3和图13可知，大扰动场景下若系统参数满足＜1，则受到扰动后系统能保持稳定运行，且满足d(,)/d＜0，与混合势理论分析结果一致，验证了大信号稳定判据的正确性。

系统发生失稳后，可通过参数调整使系统恢复稳定。以场景1为例，在3 s时将电压环积分系数IU从24增大到400，此时等效电路的最大奇异值从3.562降低为0.972，进而满足＜1，所得到的仿真波形如图14所示。由图14中可知，IU增大瞬间，电压dc和(,)函数值迅速增大，经过短暂的调节后，系统恢复稳定运行。

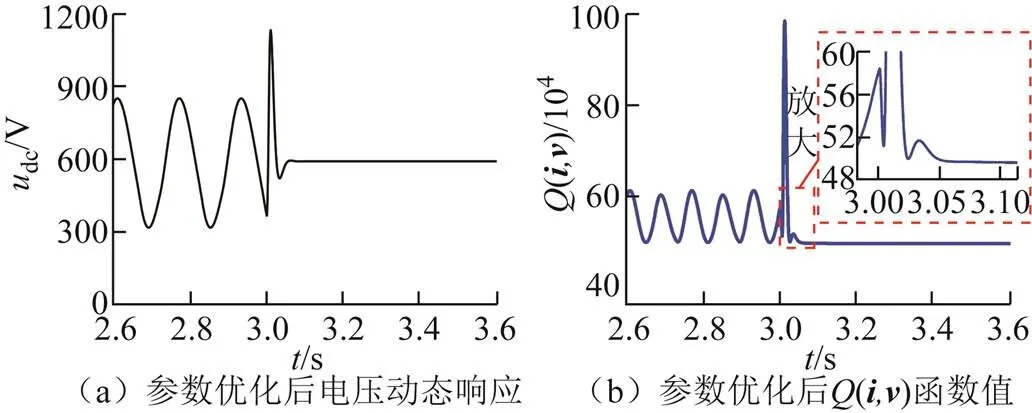
图14 参数优化后的直流电压动态响应和Q(i, v)函数值变化曲线

3.2.2 系统恒功率负载稳定运行范围验证

除系统参数满足大信号稳定判据＜1外，还需界定系统的CPL稳定运行范围。根据表2中四组参数构建了大扰动场景5～场景8，以验证求取系统CPL稳定运行边界方法的有效性。设定在2 s时接入CPL，并对其进行了大信号稳定性分析和仿真实验，结果见表4。以场景5和场景6的仿真波形为例进行详细分析，如图15所示。

表4 大扰动场景下功率边界对系统稳定性的影响

Tab.4 Influence of power boundary on stability in large disturbance cases

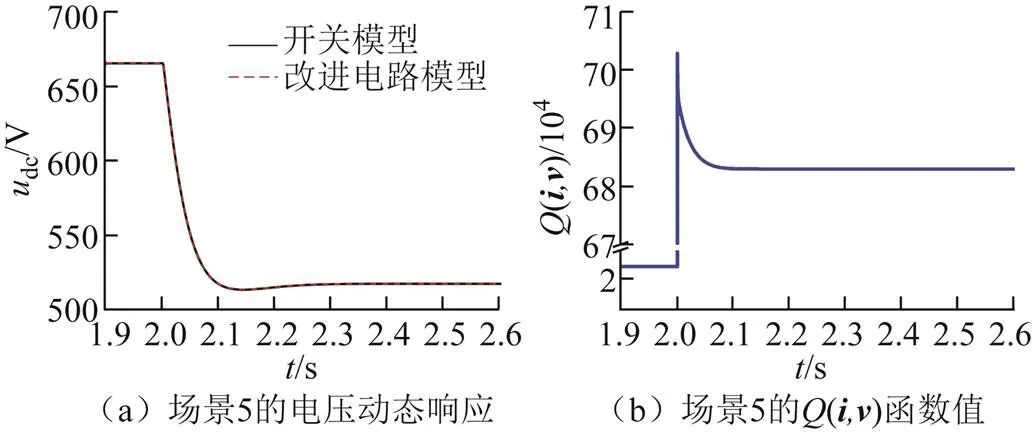
针对场景5，由图15a和图15b可知，直流电压经过快速的电压调节后到达了稳态，(,)函数值在扰动后随时间增加而单调减小到稳态值。针对场景6，虽然满足＜1但不满足CPL＜max1，故CPL功率值阶跃变化时系统将会失稳。由图15c和图15d可知，当CPL功率值阶跃到1.01max1时，直流电压和(,)函数值剧烈振荡失稳。在3.3 s时，CPL功率值阶跃到0.99max1，则系统重新恢复稳定。综合表4和图15可知，CPL功率值稳定运行边界与理论计算结果一致，验证了大信号稳定判据的正确性。

3.2.3 不同建模方法的大信号稳定判据仿真分析

为进一步对不同建模方法的大信号稳定判据进行分析，且主要考虑换流器动态响应对系统稳定性的影响，以图9为基础搭建忽略线路阻抗和并联阻性负载的直流微电网详细开关模型，进行仿真验证。仿真参数为表2中第一组参数，通过模型一、模型二和模型三得到的大信号稳定分析结果见表5，其中对三种模型分别根据式（22）、式（25）和式（29）计算系统最大可承受扰动功率。设置2 s和3 s时CPL分别发生30 kW和80 kW的阶跃扰动，其仿真结果如图16所示。

表5 扰动80 kW时系统大信号稳定判据分析结果

Tab.5 Large-signal stability analysis results of the system under 80 kW disturbance

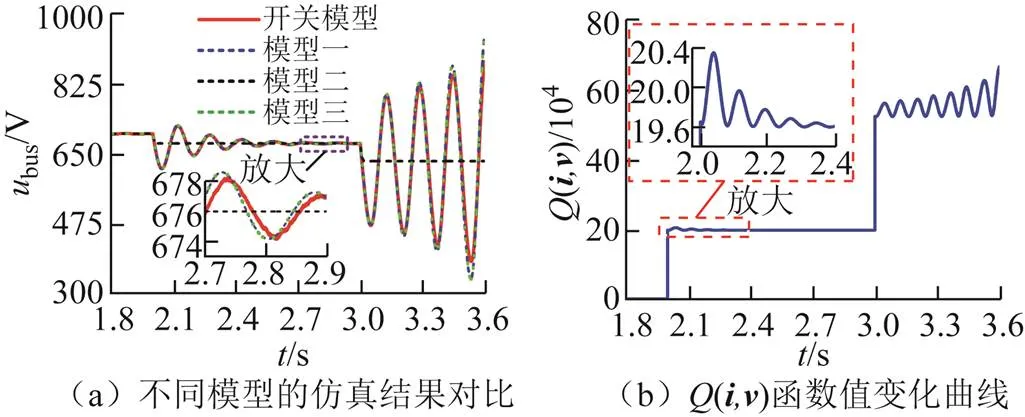
图16 不同模型仿真结果对比与Q(i, v)函数值变化曲线

由图16a可知，在2 s发生扰动时，直流电压能够保持稳定运行，开关模型与三种简化模型的稳态值相等，但模型二的动态响应过程与开关模型有明显差异；在3 s发生扰动时，直流电压失稳，模型一、模型三与开关模型的运行结果基本一致，而模型二仍保持稳定运行。由图16b可知，在2 s发生扰动时，系统能量发生了一定振荡后才达到了稳态，不满足d()/d＜0；在3 s发生扰动时，系统能量失稳。故仿真结果与模型一的大信号分析结论一致；而模型二因难以刻画换流器的动态响应，其分析结果存在一定偏差；模型三的动态响应与开关模型基本一致，然而该模型不利于应用混合势理论运算求解，具体表现为现有研究将式（26）代入式（28）中求解二阶偏导数时，忽略了积分环节等时变项的影响[21,26]，而当换流器积分系数取值较小时，系统动态响应较慢，难以快速提供系统稳定所需功率，故表5中基于模型三所得到的稳定性分析结果与开关模型的仿真结果不一致。

3.3 多端直流微电网稳定判据适应性分析

3.3.1 多端直流微电网模型及其大信号稳定判据

在源荷双端直流微电网的基础上进行扩展，建立图17所示的五端直流微电网，以进一步验证所提等效电路模型和大信号稳定判据适应性。图17中，负载侧电容L=2 mF，并联阻性负载L=20 Ω，光伏发电单元电容PV=2 mF。光伏发电单元采用电导增量法工作在最大功率点追踪模式，最大输出功率为1.32 kW。

图17 五端直流微电网结构

构建图17所示模型的混合势函数为

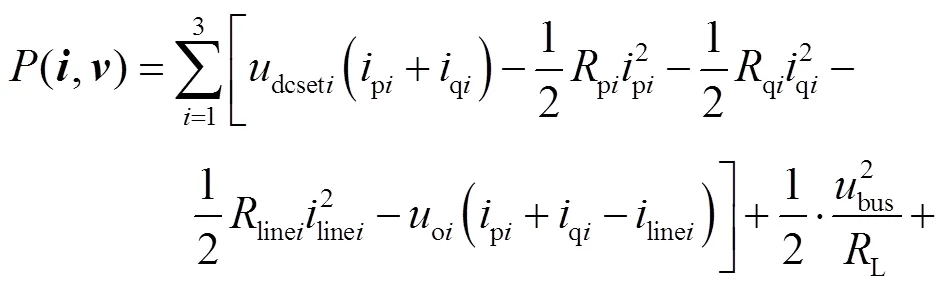
式中，dcseti为第台源换流器的直流电压设定值，=1, 2, 3；oi为第台源换流器的输出电压；pi、qi和pi、qi分别为第台源换流器等效电路模型的p支路和q支路的电阻和电流；linei、linei和linei分别为第台源换流器的线路电流、线路电阻和线路电感；PV为光伏发电单元的输出功率。

结合式（12）、式（15）和式（30）计算得到五端直流微电网的大信号稳定判据为

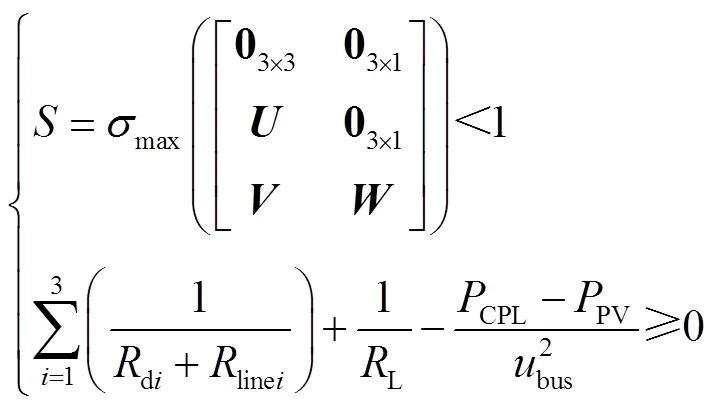
其中

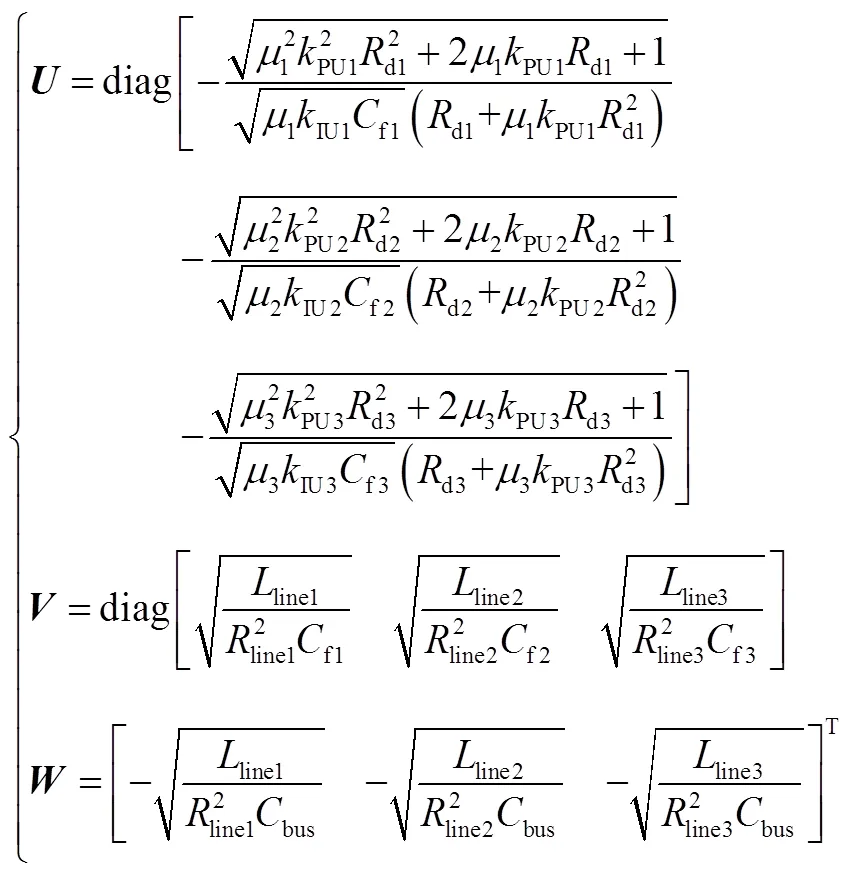
式中，μ为第台源换流器的电流转换系数；bus为直流母线等效电容，满足bus=L+PV。

设等效恒功率负载E=CPL-PV，则E的极限功率Emax为源换流器最大传输功率，由此得到CPL的稳定运行功率边界CPLmax=Emax+PV。

3.3.2 两种场景的系统稳定性验证

本节设计了场景9和场景10进行系统稳定性验证，其仿真参数见表6，表中用“/”区分场景9和场景10参数。其中场景9不满足＜1，场景10满足＜1。在2 s前系统接入光伏发电功率并进入稳态，设定在2、3、4、5、6、7 s时分别接入0.2CPLmax、0.4CPLmax、0.6CPLmax、0.8CPLmax、0.98CPLmax和1.01CPLmax的CPL功率值，其中CPLmax=4.448 kW，得到场景9和场景10的仿真波形分别如图18和图19所示。

表6 五端直流微电网仿真参数

Tab.6 Simulation parameters of five-terminals DC microgrid

图18 场景9的仿真波形

场景9中，结合式（31）计算得到=2.595＞1，由此得出场景9中系统大信号不稳定。由图18a和图18b可知，随着CPL增大，直流母线电压进入稳态所需过渡时间逐渐增加；由图18c可知，因采用Buck电路的非理想CPL和光伏的接入导致响应曲线略有波动，当CPL增大到0.8CPLmax后，(,)发生明显振荡，5.2 s时系统失去稳定。

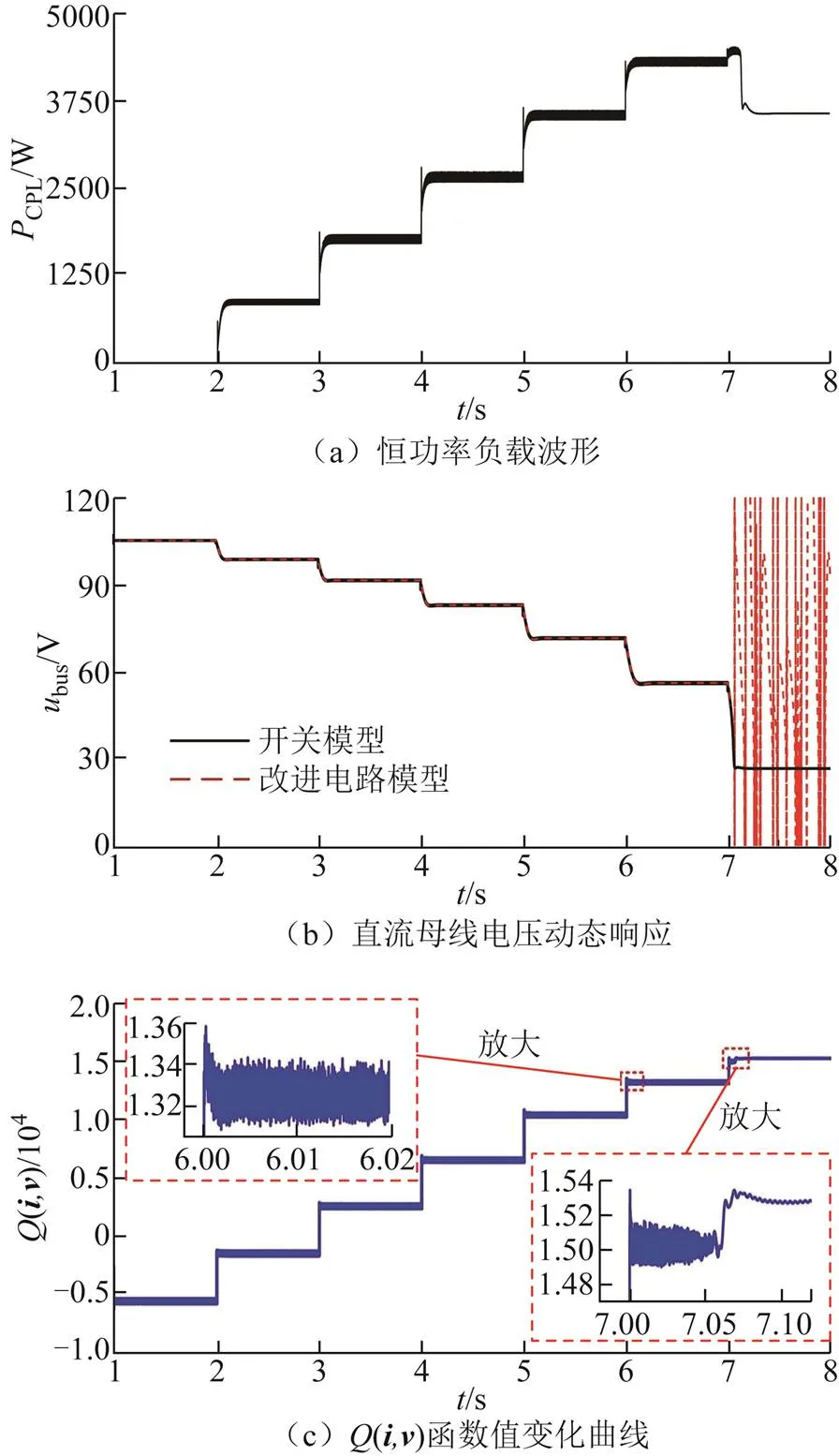
图19 场景10的仿真波形

场景10中，结合式（31）计算得到=0.973＜1，则当CPL＜CPLmax时系统是大信号稳定的。由图19a和图19b可知，当CPL发生不同程度的功率阶跃扰动时，直流母线电压能快速达到稳态值并保持平稳运行；由图19c可知，当CPL增大到1.01CPLmax后，(,)在7.05 s时发生明显跃变，系统失去稳定。由图19各分图可知，若系统参数满足＜1且CPL＜CPLmax，则系统是大信号稳定的；若系统参数不满足＜1，则系统面临大功率扰动时会失稳，与大信号稳定判据分析结果一致。

4 结论

本文以典型的直流电压下垂控制直流微电网为研究对象，针对传统大信号简化模型难以分析换流器控制参数的问题，提出了一种改进的等效电路模型，并基于混合势理论推导出直流微电网的大信号稳定判据，得出如下结论：

1）根据电压源型换流器的控制结构推导的RLC等效电路可等效变换为具备完整状态变量集的电路模型，从而利于构造混合势函数，进而可应用混合势理论得到直流微电网的大信号稳定判据和稳定域。通过判断系统是否满足＜1和CPL＜CPLmax，以及系统能量的变化趋势可对系统的大信号稳定性进行判别。

2）通过分析系统参数对大信号稳定判据和系统能量(,)的影响得知，换流器电压环比例系数、电压环积分系数、下垂系数、滤波电容和线路电阻的增大以及线路电感的减小能够提高系统大信号稳定性；增大下垂系数或线路电阻会减小系统可承受的CPL功率范围，而减小并联阻性负载功率能增加相应的CPL功率范围。

3）仅考虑直流微电网中LC滤波器和线路阻抗等参数时，因难以准确刻画换流器的动态响应，得到的大信号稳定判据可能存在较大误差。所提改进等效电路模型扩展到多端直流微电网时，仍能反映系统响应特性，进而准确求解得到系统稳定域。

[1] 赵恩盛, 韩杨, 周思宇, 等. 微电网惯量与阻尼模拟技术综述及展望[J]. 中国电机工程学报, 2022, 42(4): 1413-1428. Zhao Ensheng, Han Yang, Zhou Siyu, et al. Review and prospect of inertia and damping simulation technologies of microgrids[J]. Proceedings of the CSEE, 2022, 42(4): 1413-1428.

[2] 杨珺, 侯俊浩, 刘亚威, 等. 分布式协同控制方法及在电力系统中的应用综述[J]. 电工技术学报, 2021, 36(19): 4035-4049. Yang Jun, Hou Junhao, Liu Yawei, et al. Distributed cooperative control method and application in power system[J]. Transactions of China Electrotechnical Society, 2021, 36(19): 4035-4049.

[3] Xu Luona, Guerrero J M, Lashab A, et al. A review of DC shipboard microgrids—part I: power architectures, energy storage, and power converters[J]. IEEE Transactions on Power Electronics, 2022, 37(5): 5155-5172.

[4] Xu Qianwen, Vafamand N, Chen Linglin, et al. Review on advanced control technologies for bidirectional DC/DC converters in DC microgrids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(2): 1205-1221.

[5] Muhtadi A, Pandit D, Nguyen N, et al. Distributed energy resources based microgrid: review of architecture, control, and reliability[J]. IEEE Transactions on Industry Applications, 2021, 57(3): 2223-2235.

[6] 赵学深, 朱琳, 郭力, 等. 基于等值单机非线性模型的多换流器并联直流系统暂态稳定性分析及控制参数整定方法[J]. 中国电机工程学报, 2023, 43(4): 1389-1402. Zhao Xueshen, Zhu Lin, Guo Li, et al. Transient stability analysis and control parameters tuning method of multi-converters DC power system based on equivalent single-converter nonlinear model[J]. Proceedings of the CSEE, 2023, 43(4): 1389-1402.

[7] Chang Fangyuan, Cui Xiaofan, Wang Mengqi, et al. Region of attraction estimation for DC microgrids with constant power loads using potential theory[J]. IEEE Transactions on Smart Grid, 2021, 12(5): 3793-3808.

[8] 庄莹, 裴玮, 刘子奇, 等. 提升低压直流配电稳定性的时滞模型预测附加控制[J]. 电工技术学报, 2023, 38(12): 3248-3263. Zhuang Ying, Pei Wei, Liu Ziqi, et al. Time-delay model predictive additional control strategy to improve the stability of low-voltage DC distribution system[J]. Transactions of China Electrotechnical Society, 2023, 38(12): 3248-3263.

[9] 郑安然, 郭春义, 殷子寒, 等. 提高弱交流系统下混合多端直流输电系统小干扰稳定性的控制参数优化调节方法[J]. 电工技术学报, 2020, 35(6): 1336-1345. Zheng Anran, Guo Chunyi, Yin Zihan, et al. Optimal adjustment method of control parameters for improving small-signal stability of hybrid multi-terminal HVDC system under weak AC condition[J]. Transactions of China Electrotechnical Society, 2020, 35(6): 1336-1345.

[10] 李达, 张涛. 基于阻抗法的光储逆变器交直流建模及耦合分析[J/OL]. 电工技术学报, 2023: 1-11[2023-07-01]. DOI: 10.19595/j.cnki.1000-6753. tces. 230286. Li Da, Zhang Tao. Modeling and coupling analysis of DC and grid side of solar-storage inverter based on impedance method[J/OL]. Transactions of China Electrotechnical Society, 2023: 1-11[2023-07-01]. DOI: 10.19595/j.cnki.1000-6753.tces.230286.

[11] Li Pengfei, Guo Li, Li Xialin, et al. Reduced-order modeling and comparative dynamic analysis of DC voltage control in DC microgrids under different droop methods[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 3317-3333.

[12] 陈庆, 袁栋, 袁宇波, 等. 多电压等级直流配电系统小信号稳定性评估方法[J]. 电力系统自动化, 2022, 46(21): 80-88. Chen Qing, Yuan Dong, Yuan Yubo, et al. Small-signal stability assessment method for DC distribution system with multiple voltage levels[J]. Automation of Electric Power Systems, 2022, 46(21): 80-88.

[13] 王晴, 刘增, 韩鹏程, 等. 基于变流器输出阻抗的直流微电网下垂并联系统振荡机理与稳定边界分析[J]. 电工技术学报, 2023, 38(8): 2148-2161. Wang Qing, Liu Zeng, Han Pengcheng, et al. Analysis of oscillation mechanism and stability boundary of droop-controlled parallel converters based on output impedances of individual converters in DC microgrids[J]. Transactions of China Electrotechnical Society, 2023, 38(8): 2148-2161.

[14] Fu Xikun, Sun Jianjun, Huang Meng, et al. Large-signal stability of grid-forming and grid-following controls in voltage source converter: a comparative study[J]. IEEE Transactions on Power Electronics, 2021, 36(7): 7832-7840.

[15] Gui Yonghao, Han Renke, M Guerrero J, et al. Large-signal stability improvement of DC-DC converters in DC microgrid[J]. IEEE Transactions on Energy Conversion, 2021, 36(3): 2534-2544.

[16] Chang Fangyuan, Cui Xiaofan, Wang Mengqi, et al. Large-signal stability criteria in DC power grids with distributed-controlled converters and constant power loads[J]. IEEE Transactions on Smart Grid, 2020, 11(6): 5273-5287.

[17] 刘宿城, 李响, 秦强栋, 等. 直流微电网集群的大信号稳定性分析[J]. 电工技术学报, 2022, 37(12): 3132-3147. Liu Sucheng, Li Xiang, Qin Qiangdong, et al. Large signal stability analysis for DC microgrid clusters[J]. Transactions of China Electrotechnical Society, 2022, 37(12): 3132-3147.

[18] Liu Sucheng, Li Xiang, Xia Mengyu, et al. Takagi-sugeno multimodeling-based large signal stability analysis of DC microgrid clusters[J]. IEEE Transactions on Power Electronics, 2021, 36(11): 12670-12684.

[19] Xie Wenqiang, Han Minxiao, Cao Wenyuan, et al. System-level large-signal stability analysis of droop-controlled DC microgrids[J]. IEEE Transactions on Power Electronics, 2021, 36(4): 4224-4236.

[20] Weaver W W, Robinett R D, Wilson D G, et al. Metastability of pulse power loads using the Hamiltonian surface shaping method[J]. IEEE Transactions on Energy Conversion, 2017, 32(2): 820-828.

[21] Peng Dongdong, Huang Meng, Li Jinhua, et al. Large-signal stability criterion for parallel-connected DC–DC converters with current source equivalence[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2019, 66(12): 2037-2041.

[22] 厉泽坤, 孔力, 裴玮. 直流微电网大扰动稳定判据及关键因素分析[J]. 高电压技术, 2019, 45(12): 3993-4002. Li Zekun, Kong Li, Pei Wei. Analyses of stability criterion and key factors of DC microgrid under large disturbance[J]. High Voltage Engineering, 2019, 45(12): 3993-4002.

[23] Marx D, Magne P, Nahid-Mobarakeh B, et al. Large signal stability analysis tools in DC power systems with constant power loads and variable power loads—a review[J]. IEEE Transactions on Power Electronics, 2012, 27(4): 1773-1787.

[24] Tian Zhen, Tang Yingjie, Zha Xiaoming, et al. Hamilton-based stability criterion and attraction region estimation for grid-tied inverters under large-signal disturbances[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2022, 10(1): 413-423.

[25] 滕昌鹏, 王玉斌, 周博恺, 等. 含恒功率负载的直流微网大信号稳定性分析[J]. 电工技术学报, 2019, 34(5): 973-982. Teng Changpeng, Wang Yubin, Zhou Bokai, et al. Large-signal stability analysis of DC microgrid with constant power loads[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 973-982.

[26] Jiang Jianbo, Liu Fei, Pan Shangzhi, et al. A conservatism-free large signal stability analysis method for DC microgrid based on mixed potential theory[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 11342-11351.

[27] 杭丽君, 闫东, 胡家兵, 等. 电力电子系统建模关键技术综述及展望[J]. 中国电机工程学报, 2021, 41(9): 2966-2980. Hang Lijun, Yan Dong, Hu Jiabing, et al. Review and prospect of key modeling technologies for power electronics system[J]. Proceedings of the CSEE, 2021, 41(9): 2966-2980.

[28] 厉泽坤, 孔力, 裴玮, 等. 基于混合势函数的下垂控制直流微电网大扰动稳定性分析[J]. 电网技术, 2018, 42(11): 3725-3734. Li Zekun, Kong Li, Pei Wei, et al. Large-disturbance stability analysis of droop-controlled DC microgrid based on mixed potential function[J]. Power System Technology, 2018, 42(11): 3725-3734.

[29] Chang Fangyuan, Cui Xiaofan, Wang Mengqi, et al. Potential-based large-signal stability analysis in DC power grids with multiple constant power loads[J]. IEEE Open Access Journal of Power and Energy, 2021, 9: 16-28.

[30] Du Weijing, Zhang Junming, Zhang Yang, et al. Stability criterion for cascaded system with constant power load[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1843-1851.

[31] Wang Chengshan, Li Xialin, Guo Li, et al. A nonlinear-disturbance-observer-based DC-bus voltage control for a hybrid AC/DC microgrid[J]. IEEE Transactions on Power Electronics, 2014, 29(11): 6162-6177.

[32] Li Xialin, Guo Li, Huang Di, et al. A reduced RLC impedance model for dynamic stability analysis of PI-controller-based DC voltage control of generic source-load two-terminal DC systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2021, 9(6): 7264-7277.

[33] 曾正, 邵伟华, 宋春伟, 等. 电压源逆变器典型控制方法的电路本质分析[J]. 中国电机工程学报, 2016, 36(18): 4980-4989, 5123. Zeng Zheng, Shao Weihua, Song Chunwei, et al. Circuit-based analysis of typical control schemes of voltage-source inverter[J]. Proceedings of the CSEE, 2016, 36(18): 4980-4989, 5123.

[34] Yuan Hao, Yuan Xiaoming, Hu Jiabing. Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control timescale[J]. IEEE Transactions on Power Systems, 2017, 32(5): 3981-3991.

[35] Brayton R K, Moser J K. A theory of nonlinear networks. II[J]. Quarterly of Applied Mathematics, 1964, 22(2): 81-104.

[36] LaSalle J. Some extensions of Liapunov’s second method[J]. IRE Transactions on Circuit Theory, 1960, 7(4): 520-527.

Large-Signal Stability Analysis for DC Microgrids Based on the Improved Equivalent Circuit Model

Wang Li1Tan Zhenjie1Zeng Xiangjun1Zhao Bin1Zheng Yueqiu2

（1. School of Electrical and Information Engineering Changsha University of Science and Technology Changsha 410114 China 2. Tibet East China Hydropower Equipment Co. Ltd Lhasa 851414 China）

Simplified modeling has proven effective in analyzing the large-signal stability of high-order nonlinear DC microgrids (DCMGs). However, the traditional simplified models primarily focus on the parameters such as LC filters and line impedances, making it difficult to analyze the impact of converter control parameters. Additionally, the established criteria do not accurately reflect the stability region of DCMGs. To address these limitations, an improved equivalent circuit model with a complete set of state variables for DC voltage droop control converters was proposed. Compared to the traditional simplified models, this model provides a more accurate description of the system’s low-frequency response, enabling precise analysis of the large-signal stability of DCMGs.

The circuit model of the output impedance of DC voltage droop control converters is first derived from its output voltage dynamic equation. Subsequently, this model undergoes an equivalent transformation, resulting in an improved equivalent circuit model that incorporates a complete set of state variables for the DC voltage droop control converter. By combining the improved equivalent circuit model with constant power load (CPL) and parallel resistive load, an equivalent nonlinear circuit model is derived. The proposed model facilitates the construction of the mixed potential function, allowing for the derivation of both the large-signal stability criterion and stability region of the DCMGs. So that the parameters domain and power boundary of the system are calculated. Lastly, the energy indicatorthrough the application of the LaSalle invariant set theorem is obtained, which helps to capture the trends in system stability changes. The large-signal stability of the system can be assessed based on the conditions of＜1 andCPL＜CPLmax, along with the dynamic changes observed in the energy indicator.Additionally, the derived large-signal stability criterion can guide the optimization of control parameters.

The simulation results demonstrate the alignment between the DC voltage dynamic responses of the proposed model and those of the detailed model. The energy indicator reflects the degree of fluctuation in the DC voltage response. Enhancing the large-signal stability of DCMGs can be achieved by increasing the voltage loop proportional and integral gain, droop gain, filter capacitance and line resistance, while decreasing line inductance. Increasing the droop gain, line resistance, and parallel resistive load will result in a reduction of the CPL boundary. Comparing the large-signal stability criteria based on different modeling methods reveals errors in the analysis results obtained from traditional models. These errors occur due to the challenges in describing the dynamic response of the converters adequately or when the crucial parameters are overlooked during the calculations. Finally, based on the simulation results obtained for both two-terminal and five-terminal DCMGs, it can be seen that stability can be achieved in the event of large disturbances when the system satisfies the maximum singular value＜1 and when the CPL power valueCPLremains below the threshold ofCPLmax. Conversely, if the system fails to meet＜1 orCPL＜CPLmax, instability occurs during large disturbances.

DC microgrid, large-signal stability, equivalent model, DC voltage control, mixed potential theory

10.19595/j.cnki.1000-6753.tces.230398

TM711

国家自然科学基金（52107071）、湖南省自然科学基金（2023JJ40043）和2022年长沙理工大学专业学位研究生“实践创新与创业能力提升计划”（CLSJCX22075）资助项目。

2023-04-01

2023-05-18

王 力 男，1990年生，讲师，硕士生导师，研究方向为电力系统运行与控制。E-mail：wangli@csust.edu.cn（通信作者）

谭振杰 男，1998年生，硕士研究生，研究方向为直流微电网稳定性分析。E-mail：tanzhenjie147@163.com

（编辑 李 冰）