下肢运动状态特征对裤装臀围的影响分析
吴冬雪, 刘让同,2,3, 于媛媛, 李淑静, 韩 赟
(1.中原工学院, 河南 郑州 451191; 2.先进纺织装备技术省部共建协同创新中心, 河南 郑州 451191;3.河南省功能纺织材料重点实验室, 河南 郑州 451191)

为此本文基于裤装合体不束缚的基本思想,提出基于人体动态特征的臀围数学模型,根据下肢特征和下肢运动规律进行臀围数学模型的推导,探究了下肢动态特征参数对臀围的影响,探讨了裤装臀围的计算方法,以期为臀围结构设计提供依据,也为服装定制解决方案提供理论参考。
1 人体臀围模型及参数
基于合体不束缚考虑,裤装的结构尺寸明显与人体下肢特征参数及腿部运动状态参数密切相关。人体下肢特征参数包括臀围宽度、臀围厚度、腿部倾斜角、腿干长等;腿部运动状态参数主要包括腿部抬起角度和抬起方向角度。由于腿部的运动状态会使人体结构参数产生变化,使裤装的结构尺寸也相应地发生改变,显然人体下肢特征参数提供裤装合体的依据,腿部运动状态参数则提供裤装不束缚的依据。特别对裤装臀围来说,所需最小臀围应等于产生增量后的人体臀围,明显是与人体下肢特征参数及腿部运动状态参数相关的函数,其中下肢特征参数和腿部运动状态参数为自变量,裤装所需最小臀围为因变量。
1.1 站立无运动时臀围特征


图1 臀部骨骼特征(背面)及臀围向椭圆的拟化Fig.1 Hip skeletal features (dorsal) and anthropomorphism of hip circumference towards ellipse

(1)
1.2 考虑下肢运动状态参数的臀围模型
下肢运动状态参数包括方向角度α与抬起角度β2个角度,均是影响臀围尺寸的重要因素。
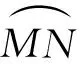

图2 腿部在动态参数(α,β)下的俯视图与空间示意图Fig.2 Top view and spatial schematic of leg at dynamic parameters (α, β). (a) Hip circumference cross-sectional view; (b) Lower limb coordinate system; (c) Leg lifting space diagram
方向角度α为腿部中心轴在臀围水平面投影与X轴的夹角,为水平角,决定着抬腿方向;抬起角度β为腿部中心轴与人体竖轴Z的夹角,决定抬腿范围,如图2(a)、(c)所示。任意(α,β)组合都对应着下肢唯一的运动状态。当α=0°时,下肢做侧抬腿运动,当α=π/2时,做前抬腿运动。由于腿部有一定直径,当α>π/2时,腿部做内旋运动,会发生脂肪肌肉的挤压,不符合模型设定,因此本文只做下肢前侧抬腿讨论,即α∈[0,π/2]。
2 裤装臀围模型的构建
为满足抬腿时不受束缚的需求,裤装的最小臀围H应等于抬腿运动变化后的人体臀围,为简化推导,在计算臀围时将腿部弧度忽略不计,暂不考虑裤装面料厚度与弹性的影响。
2.1 单侧抬腿时的裤装臀围

2.1.1PM与PN的长度

由两点间距离公式解出PM与PN距离为:
(2)
2.1.2QP的长度
在与X轴成角度α的平面中取静止时的腿部切片即梯形QADE,如图2(c)所示,经旋转切片QADE位置变化到QA′D′E,其运动轨迹如图3所示,其中∠QAE表示腿部倾斜角θt,由于腿部上粗下窄,腿部倾斜角θt小于π/2。

图3 腿部切片运动的多种状态Fig.3 States of leg movement
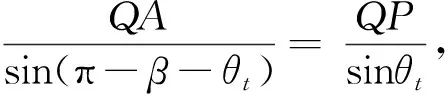
(3)

2.1.3β的范围


(4)
综上所述,任意单抬腿(α,β)状态,H为
(5)
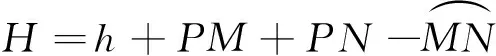
其中:
2.2 双侧抬腿时的裤装臀围
双抬腿状态一般体现在弯腰、坐着等动作,即上半身会与双腿成一定的夹角。为保持平衡双腿会呈现相同的运动状态参数(α、β),点P会存在一个关于Y轴对称的P′点,如图4所示。
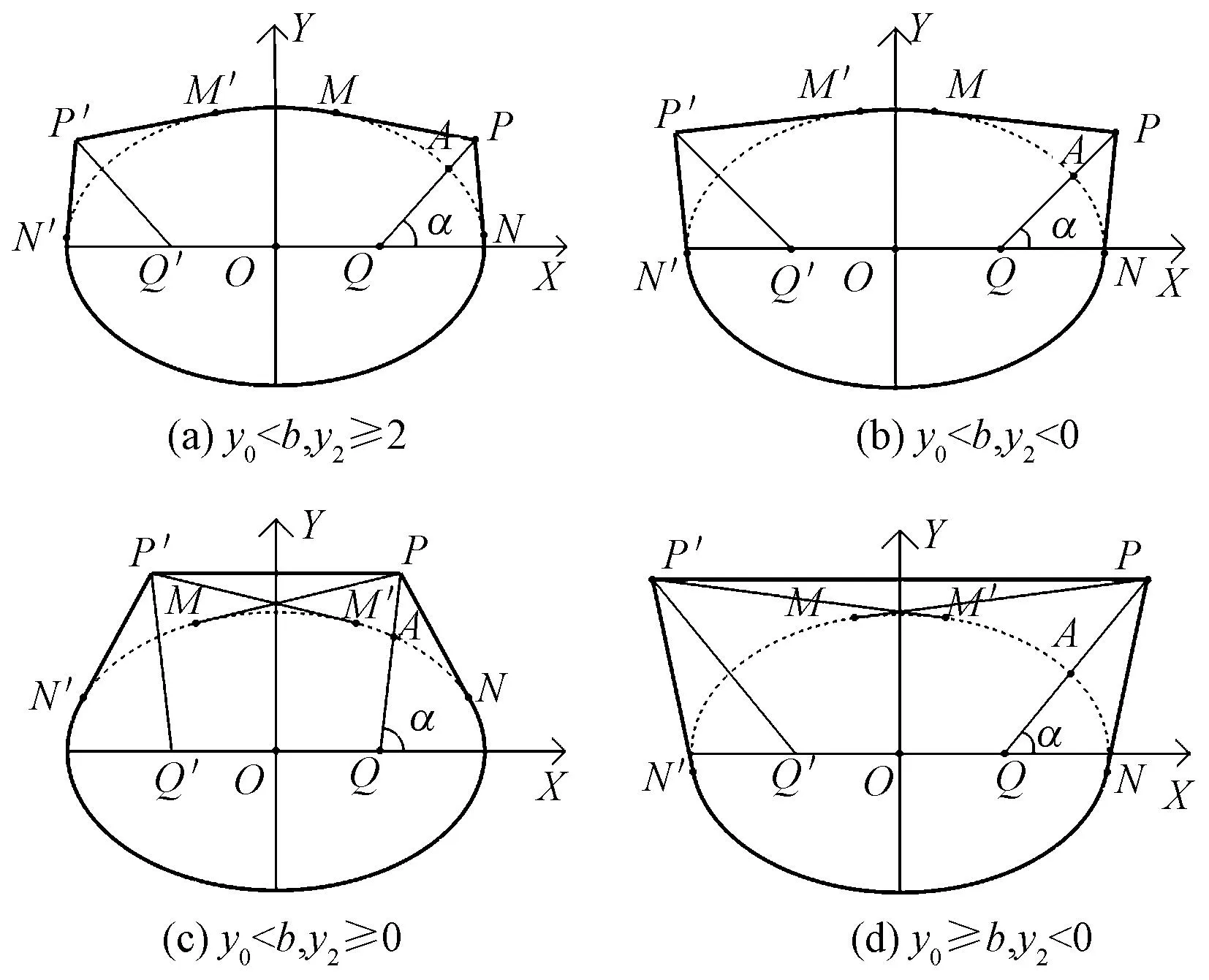
图4 双侧抬腿时臀围的4种情况Fig.4 Classification of hip circumference in bilateral leg lifts
在双抬腿状态下,臀围的计算依照点P、N的位置有4种形式:当P点的纵坐标y0 (6) 由式(5)、(6)可见臀围H与人体特征参数(a、b、θt)以及状态参数(α、β)相关。在探究臀围与状态参数关系时,利用控制变量法进行分析,其中被试者人体特征数据为:a=17 cm,b=12 cm,θt=85°。 为探究抬起角度β对臀围的影响,保持其它条件一定,分别在3种抬腿方向进行计算,即α=0°(侧抬腿),α=45°(前侧方向抬腿),α=90°(前抬腿),如图5所示。可看出,单侧抬腿与双侧抬腿时臀围大小均随着抬起角度β的增加而增加,且增加的速度不断增大,在80°以后曲线斜率急剧增加,变化更为明显。为了能够清楚看出不同β条件对臀围的影响,将图5拆成0°~60°和60°~90° 2个区间显示,显然在抬起角度β小于60°时,裤装臀围的变化比较平缓,而当β大于60°时,臀围的变化幅度很大,可能出现与实际不符的失真。 图5 臀围与抬起角度β之间的关系Fig.5 Relationship between hip circumference and lifting angle 图5显示了单抬腿和双抬腿的变化趋势,其中双抬腿状态下的臀围对抬起角度更为敏感,变化幅度更大。不同的抬腿方向也制约着臀围的大小,很明显单腿侧抬腿使臀围增加幅度最大。 图6示出裤装臀围随方向角度α(单抬腿和双抬腿时)的变化曲线,其中β=45°。可看出,单侧抬腿与双侧抬腿的状态臀围的变化趋势区别很大,当单侧抬腿的抬起角度为45°时,裤装臀围会随着方向角度α的增大(即从侧抬腿转向前抬腿的过程中)呈先减小后增大的趋势,在α=0°(即腿部仅向侧面抬起)时具有最大值,此时裤装臀围为99.50 cm,其中净臀围h=91.78 cm;在双腿侧抬起45°时,随着α的增大,裤装臀围逐渐变小,且在60°以后迅速变小,当α=0°(即双腿均侧抬)时裤装臀围具有最大值,H=107.21 cm。 图6 臀围与方向角度α之间的关系Fig.6 Relationship between hip circumference and orientation angle α 在日常人体运动中,基础抬腿运动中的角度β相对会比较小,一般不大于60°,如最常见的步行角度在45°~60°之间,而在弯腰、坐姿等人体状态时,抬腿运动角度β会大些,一般在60°以上。下肢侧向角度的抬腿运动幅度均不会很大,满足前抬腿运动亦可保证侧抬等不受束缚。为此,下文分2种情况进行讨论。 (7) 图7 步行状态分析Fig.7 Walking condition analysis 取5组被试者人体数据代入式(1)、(7)中,计算净臀围值和抬腿角度后,代入式(5)中得到步行状态裤装臀围值,结果如表1所示。其数据显示,裤装臀围与人体特征参数和下肢运动状态参数密切相关。为了得到步幅对臀围的影响,保持人体其它数据一致,选择同一被试者做不同步幅测试(样本2、6),步幅从58 cm增至67 cm,其裤装臀围增量从2.43 cm增至5.23 cm,显然步幅的增加使其抬起角度增加了近9°,使裤装臀围值增加近3 cm,因此在运动裤装设计时要做到不束缚人体,除要考虑人体因素外还要依据运动的幅度做调整,其臀围设计需要考虑个体的步幅习惯。 表1 臀围模型计算结果Tab.1 Hip circumference calculated from the model 不难看出,在一定的抬腿方向上,臀围均会随着抬起角度的增加而增加,且增量越来越大,尤其在60°以上,曲线斜率过大,对于坐姿等状态,身体与腿部夹角达到60°以上,在这种较大抬腿角度情况下,如果仿照模型计算,可能导致裤装臀围过大失真,呈现过于宽松不美观,不符合实际情况,需要对模型进行修正。当抬腿角度β在60°以上时(方向角度保持为α=90°),裤装臀围线不再与腰围线平行,裤装在臀围线附近产生了褶皱堆积,如图8所示。 图8 坐姿臀围线的变化Fig.8 Hip line change in sitting position 由于臀围与抬起角度β呈正相关,因此满足坐姿状态的臀围值也会保证抬起角度在90°以下时均不受裤装束缚。当身体与腿部呈90°时,臀部皮肤脂肪会向上下2个方向延展,但臀围椭圆的长短半轴不变。坐姿状态下由于重力使臀部挤压变形,会使臀围椭圆的长半轴增加。由于不同脂肪肌肉密度的人处于坐姿状态时增加的宽度不一致,因此引入坐宽参数,即坐姿时的臀围椭圆长轴2a1,经测试发现a1≈a+(0.5~1.5)。由于挤压面在臀凸点下方,坐姿下的臀围椭圆短半轴不受影响。 取5组被试者数据代入式(1)得到坐姿臀围与臀围增加量,结果列于表2。其中样本2、4是同一被试者在不同时期数据,由于胖瘦不同,发现其坐宽参数不同,导致臀围增加量差异也较大。可见,即使是同一被试者,不同时期的人体数据会发生变化,在进行服装定制时需要实时量取。 表2 坐姿臀围计算结果Tab.2 Hip circumference under sitting position 在确定裤装臀围时,应把满足多种运动需求得到的最大值作为选择依据。例如:日常基本的裤装应满足步行及坐姿的基本状态,在被试者1中,步行臀围88.30 cm,坐姿臀围88.98 cm,则选取坐姿臀围作为裤装最小臀围,其臀围最大增加量为3.43 cm,在实际应用中放松量取4 cm左右。 本文研究了人在运动状态下的臀围与其人体截面形态变化的关系,通过对臀围数学模型的构建,讨论了裤装臀围与人体特征参数、下肢状态参数之间的关系,建立了考虑下肢动态参数的臀围模型。 下肢动态参数用方向角度α与抬起角度β描述,当α=0°时表示侧抬腿,当α=90°时表示前抬腿。在单侧抬腿状态下,臀围随着α的增加呈现先减小后增大的趋势,且在α=0°时臀围取得最大值;在双侧抬腿状态时,臀围与方向角度α变化呈现负相关关系,且在α=0°时臀围取得最大值;侧抬腿状态对臀围影响要大于前抬腿的影响。抬起角度β表示抬腿角度的大小,与臀围呈正相关关系。在抬起角度β≤60°时,臀围线与腰围平行,裤装不束缚人体,臀围线处也不产生褶皱堆积现象,裤装较为美观,可按个人运动需求角度范围计算裤装臀围值;在β>60°时,臀围线随身体倾斜,裤装不束缚人体但会在臀围线附近产生褶皱堆积,需要使用坐宽参数2a1代替臀围宽度2a。 在下肢多种运动状态下选取臀围变化后的最大值作为不束缚人体的裤装臀围最小值。模型解决了下肢运动状态对裤装臀围的影响问题,可为裤装臀围制版提供理论依据,为服装定制提供理论参考。3 分析与讨论
3.1 抬起角度β对臀围的影响

3.2 方向角度α对臀围的影响

4 模型应用及优化
4.1 抬起角度β≤60°时裤装臀围计算
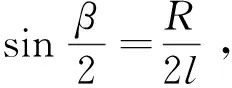


4.2 抬起角度β>60°时的臀围计算
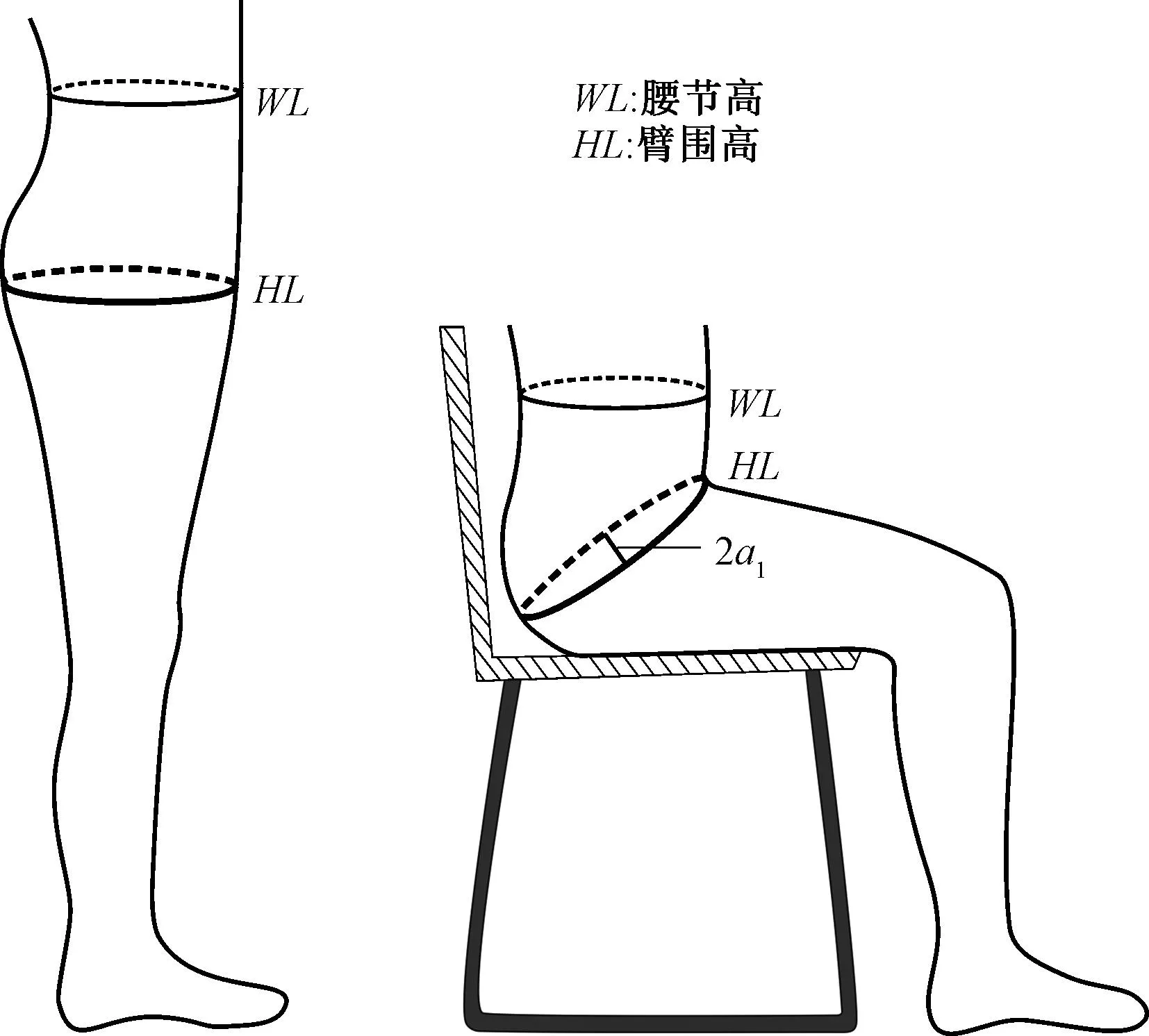
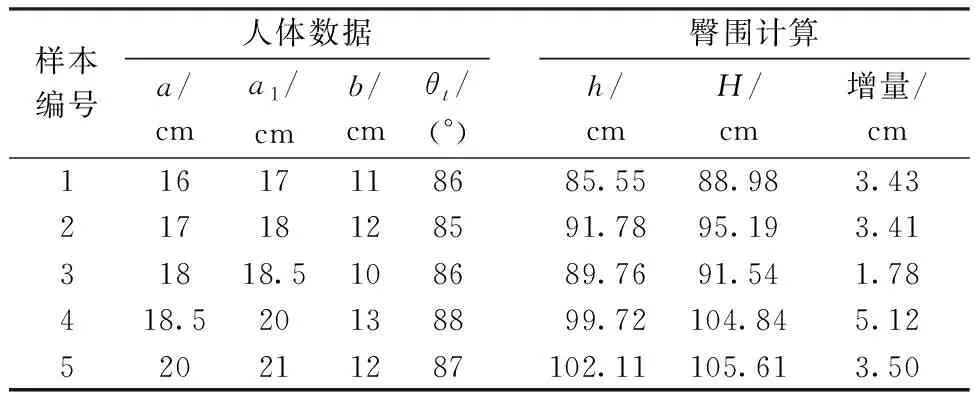
4.3 应用原则
5 结 论

