基于PSO-ELM组合算法的热力站负荷预测研究*
马文菁 郭晓杰 曹姗姗 孙春华 夏国强 齐承英
(河北工业大学,天津)
0 引言
对热负荷的准确预测是实现供热系统优化控制和节能运行的前提。常用的预测方法可以分为白箱法、黑箱法和灰箱法[1]。其中,黑箱法是基于数据驱动的预测方法,仅靠输入参数即可得到负荷预测值。基于机器学习的黑箱预测算法在供热领域得到了广泛的应用,包括人工神经网络(artificial neural network, ANN)[2]、极限学习机(extreme learning machine, ELM)[3]、支持向量回归(support vector regression, SVR)[4]、随机森林(random forest,RF)[5]等。
ELM算法是由新加波南洋理工大学黄广斌教授提出的,具有泛化能力较好、处理速度快的优点[6-7]。但该方法的输入权值和隐含层阈值是随机产生的[8],导致预测结果的稳定性不足[9]。因此,本文引入粒子群优化(particle swarm optimization, PSO)算法对ELM的输入权值、隐含层阈值进行优化,并通过案例验证粒子群优化极限学习机(PSO-ELM)算法的优势。
1 负荷预测方法
1.1 极限学习机(ELM)
ELM算法是由单隐层前馈神经网络(SLFNs)算法发展而来。图1为典型的ELM网络结构,主要包括输入层、隐含层和输出层[10]。
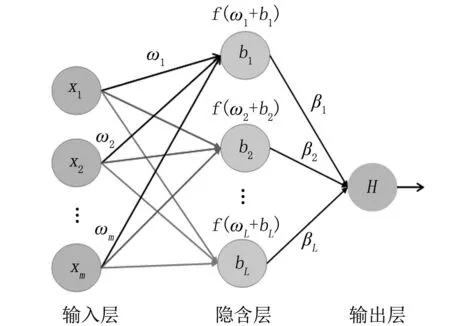
注:x1~xm为输入变量;b1~bL为隐含层的节点偏置;H为输出函数;m、L分别为输入层、隐含层的节点个数;ωi为连接输入层节点i与隐含层节点j的输入权重;βj为连接隐含层节点j与输出节点的输出权重。
对于输入样本为X且隐含层节点数为L的ELM网络结构,隐含层输出函数矩阵H表示为
(1)
式中g(x)为激活函数。

(2)
式中H+为隐含层输出函数H的Moore-Penrose广义逆矩阵。
1.2 粒子群优化(PSO)算法
PSO算法是一种群体智能模型优化算法,在模型中,每个粒子都代表优化问题的解。粒子的速度决定自身运动的距离和方向,通过不断迭代跟踪个体极值pbest和群体极值gbest,更新自身位置,获得问题的全局最优解[11]。
设种群规模为N的粒子群在D维空间构成的种群为M=[M1,M2,…,Mn],第j个粒子在空间中的位置表示为Mj=[Mj1,Mj2,…,MjD],速度表示为Vj=[Vj1,Vj2,…,VjD]。将第j个粒子的个体最优位置即个体极值表示为pj=[pj1,pj2,…,pjD],群体极值表示为pg=[pg1,pg2,…,pgD],则速度和位置的更新公式为
(3)
(4)
式(3)、(4)中 下标d为粒子的维度空间,d=1,2,3,…,D;φ为该粒子对原来运动速度的保持程度,即惯性权重;c1、c2为学习因子,c1为该粒子保持自身个体极值的程度,c2为该粒子对全局的群体极值学习程度的系数;r1、r2为0~1之间的随机数;t为迭代次数。
PSO在每次迭代中需要根据适应度函数来计算粒子所处位置的适应度,评价粒子的优劣。本文以所有预测样本预测误差的欧几里得范数作为适应度函数,定义见式(5)。由此适应度值更新个体极值pbest和群体极值gbest,直到满足终止条件,即达到最小误差或最大迭代次数。
(5)

1.3 PSO-ELM组合算法
ELM的输入与隐含层之间连接的权值ω和偏置b是随机产生的,会造成预测结果不稳定,为此本文引入PSO对ω和b进行优化。主要流程为:
1) 确定输入和输出样本。根据热负荷相关性分析选择合适的影响因素,包括室外温度、历史负荷、历史供回水温度、历史流量等。
2) 对输入和输出数据进行归一化处理。
3) 确定ELM的隐含层节点个数L和激活函数g(x),并由ELM随机产生的权重ω和偏置b作为PSO优化的变量。
4) 初始化PSO各参数,包括学习因子c1和c2、最大迭代次数、惯性权重φ,并规定粒子速度和位置的范围。
5) 训练ELM,并根据适应度函数求出个体最佳pbest和全局最优值gbest。
6) 根据式(3)、(4)更新速度和位置,在达到终止条件时输出pbest和gbest。
7) 根据PSO确定的权值ω和偏置b,将测试集输入模型。
8) 对PSO-ELM组合算法进行有效性和精确性评价。
采用PSO-ELM组合算法对热负荷进行预测,流程见图2。
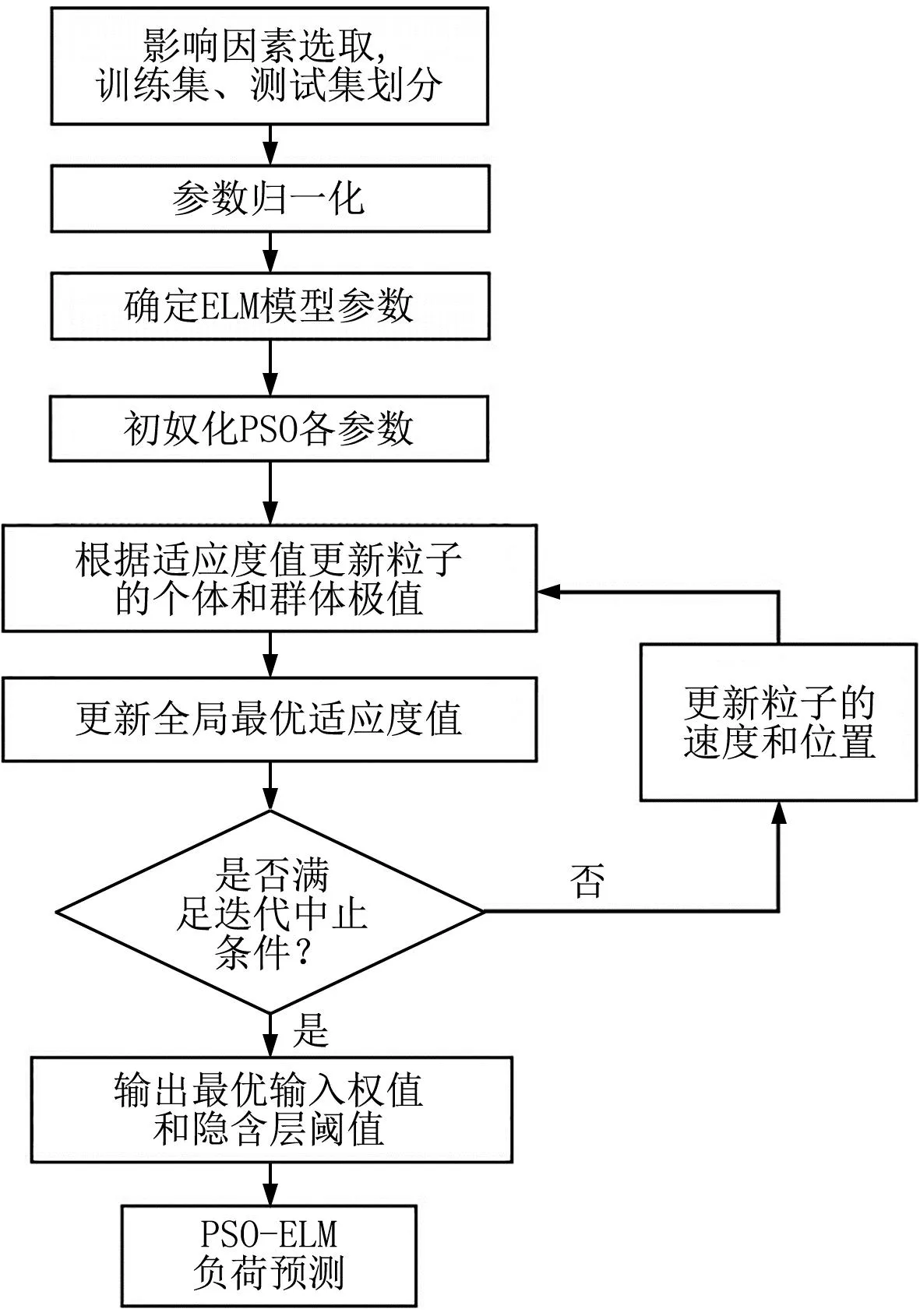
图2 PSO-ELM组合算法预测热负荷流程
1.4 评价指标
选取算法的评价指标见式(6)~(8),包括平均绝对误差(EMAE)、均方根误差(ERMSE)和平均绝对百分比误差(EMAPE)。3个指标的数值越小,模型预测精度越高。
(6)
(7)
(8)
2 结果与分析
2.1 研究对象
以天津市某小区热力站为研究对象。该热力站安装了自动控制装置,可实现数据采集与远程传输。其中采集参数包括室外温度、一次供回水温度、二次供回水温度、瞬时流量和热量,采集周期为10 min。应用该热力站2018年11月16日至2019年2月20日的运行数据进行算法的训练与验证。由于数据采集设备故障或通讯异常等原因,原始数据需要经过预处理。采用四分位法剔除异常值,由临近点的线性趋势来补充缺失值,并对长期缺失数据的日期进行删除。本研究预测热力站未来2 h的热负荷,在剔除异常数据后,由式(9)将采集参数处理为时间步长为2 h的数据集。
(9)
式中S为每2 h热负荷数据的平均值;Si为第i个参数值。
2.2 算法输入参数的确定
本研究采用皮尔逊相关系数r[12]对热负荷影响因素进行分析。r∈[-1,1],r>0表示正相关,r<0表示负相关。|r|越大,相关性越强。|r|≥0.8视为高度相关;0.5≤|r|<0.8视为中度相关;|r|<0.5视为低度相关,应当不予考虑。各影响因素的相关性分析结果见表1。由表1可知,历史热负荷Qi-n、室外温度tw、一次供/回水温度tg1,i-1/th1,i-1、二次供/回水温度tg2,i-1/th2,i-1和二次流量G2,i-1与热负荷的r均大于0.5。其中,前24个周期的历史热负荷与热负荷的r都在0.7以上,为了避免输入参数集合过大,选取r>0.8的前15个周期(30 h)的历史热负荷。而二次供回水压差Δp2,i-1和一次流量G1,i-1与热负荷的r均小于0.5,予以剔除。基础输入参数集合记为A={tg1,i-1,th1,i-1,tg2,i-1,th2,i-1,G2,i-1,tw,Qi-1,Qi-2,…,Qi-14,Qi-15}。

表1 各影响因素的相关系数
2.3 PSO-ELM预测结果
以第2.2节中筛选集合A为输入参数,2018年11月16日至12月24日的运行数据为训练集,2018年12月25—31日的运行数据为测试集,对PSO-ELM的预测效果进行验证。
首先,应用ELM方法在不调节任何参数的情况下进行1 000次预测,记录预测值的最大值、最小值和平均值3组数据,以10×1 000次预测为1组,记录30个EMAPE,并进行10组预测。图3为10组预测结果的EMAPE箱型图。由图3可知,该模型在10组预测中EMAPE最大为16.73%,最小为4.93%。在不调节参数的情况下,预测结果并不稳定,这是权值ω和隐含层偏置b随机产生造成的。
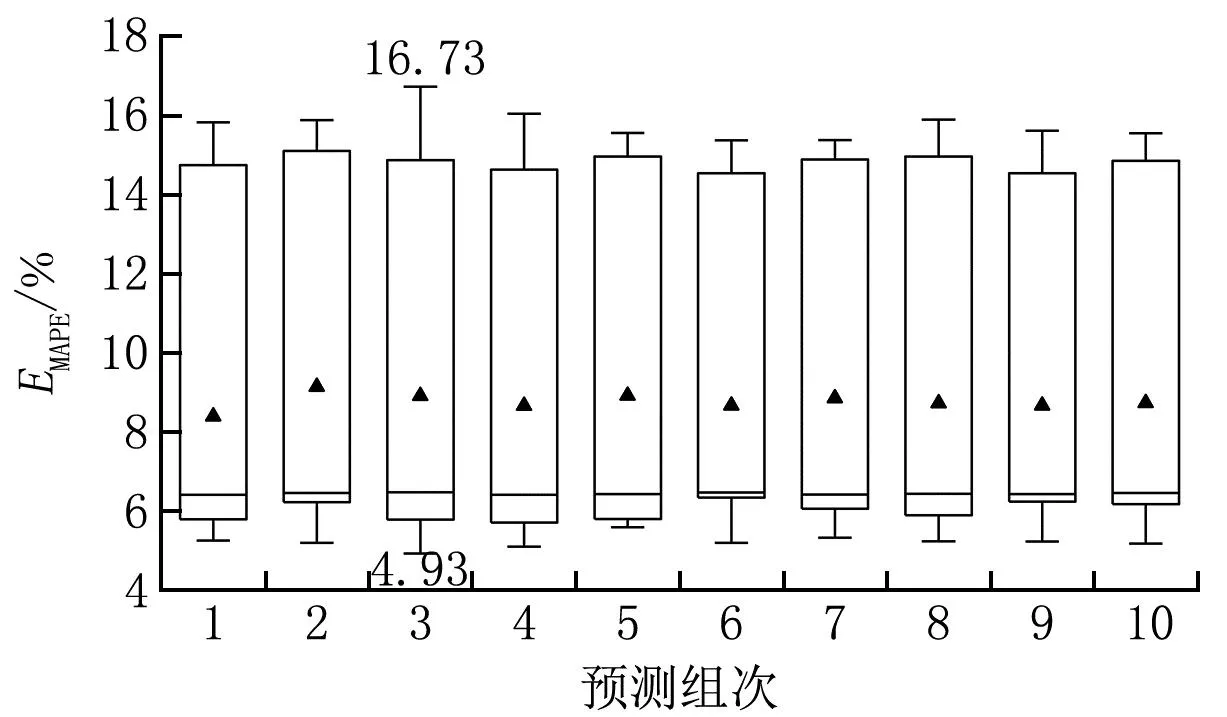
图3 ELM模型10组预测的EMAPE箱型图
然后,应用PSO-ELM组合算法对热负荷进行预测。PSO算法的参数设置为:粒子搜索维度为2,种群规模为30,最大迭代次数为50,学习因子c1=1、c2=2,位置区间为[-1,1],速度区间为[0,1],ELM隐含层神经元的数量为20,激活函数为sig函数。
PSO-ELM和ELM的预测结果和绝对误差见图4、5。由图4可知,整体上,PSO-ELM预测结果比ELM预测结果更接近实际值。由图5可知,多数情况下PSO-ELM预测结果的绝对误差在-1.44~0.17 GJ之间,最大为13.70 GJ;多数情况下ELM预测结果的绝对误差在0.93~3.38 GJ之间,最大为18.00 GJ。

图4 PSO-ELM与ELM预测结果对比
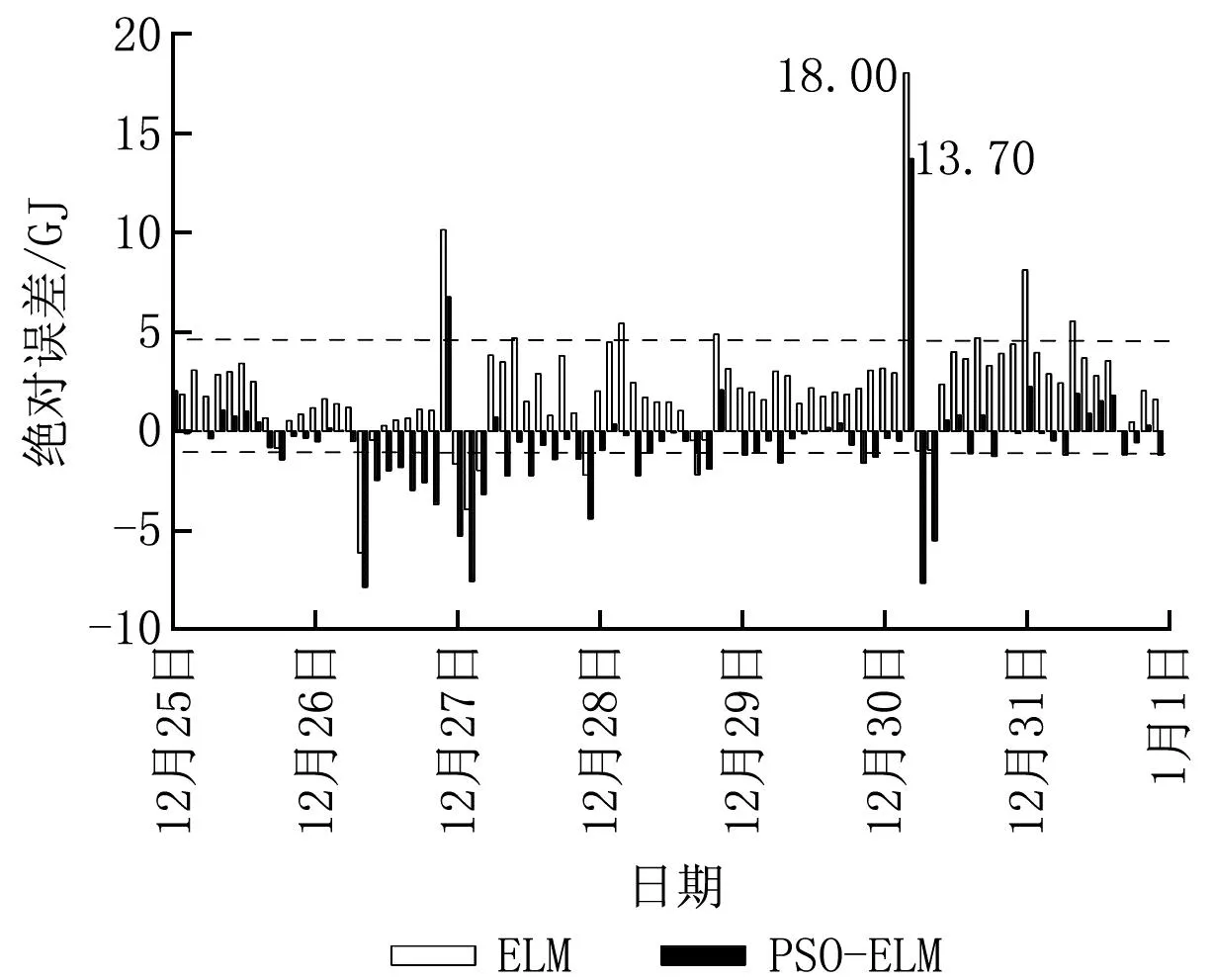
图5 PSO-ELM与ELM预测结果的绝对误差对比
2.4 预测精度对比
2.4.1不同特征组合下的预测精度
为分析不同特征组合下模型的预测精度,本研究将热负荷影响因素组合成3个特征集,将特征集A1中的输入参数依次去除供回水温度参数和流量参数,构成特征集A2和特征集A3,详细信息见表2。

表2 不同参数构成的特征集
表3给出了ELM、PSO-ELM、SVR、PSO-SVR(粒子群优化支持向量回归)分别在特征集A1~A3上的预测误差。4种算法均在特征集A3上误差最小,即室外温度和前15个周期热负荷的特征组合。其中PSO-ELM误差最小,EMAE、ERMSE和EMAPE分别为1.64 GJ、2.73 GJ和3.52%。

表3 4种算法在特征集A1、A2和A3上的预测误差
2.4.2不同负荷变化幅度下的预测精度
由图4可知,在负荷的2个突变点,算法的误差大于其他时刻。为研究不同负荷变化幅度下模型的预测精度,定义负荷变化率δmax,见式(10)。以2.4.1节中预测误差最低的特征集A3为参照,并根据δmax筛选得到A3-1和A3-22个变化幅度不同的特征集,见表4。

表4 特征集A3-1和A3-2训练集和测试集的划分

(10)
式中τ为时间,h,取2 h。
4种算法在特征集A3-1和A3-2上的预测结果见图6。由图6a可知:在12月20日,热负荷从36.11 GJ突变至24.66 GJ,预测值明显高于实际值;在此之前热负荷变化平稳,预测值与实际值十分接近。图6b中热负荷变化相对平稳,4种算法的预测值均接近实际值。
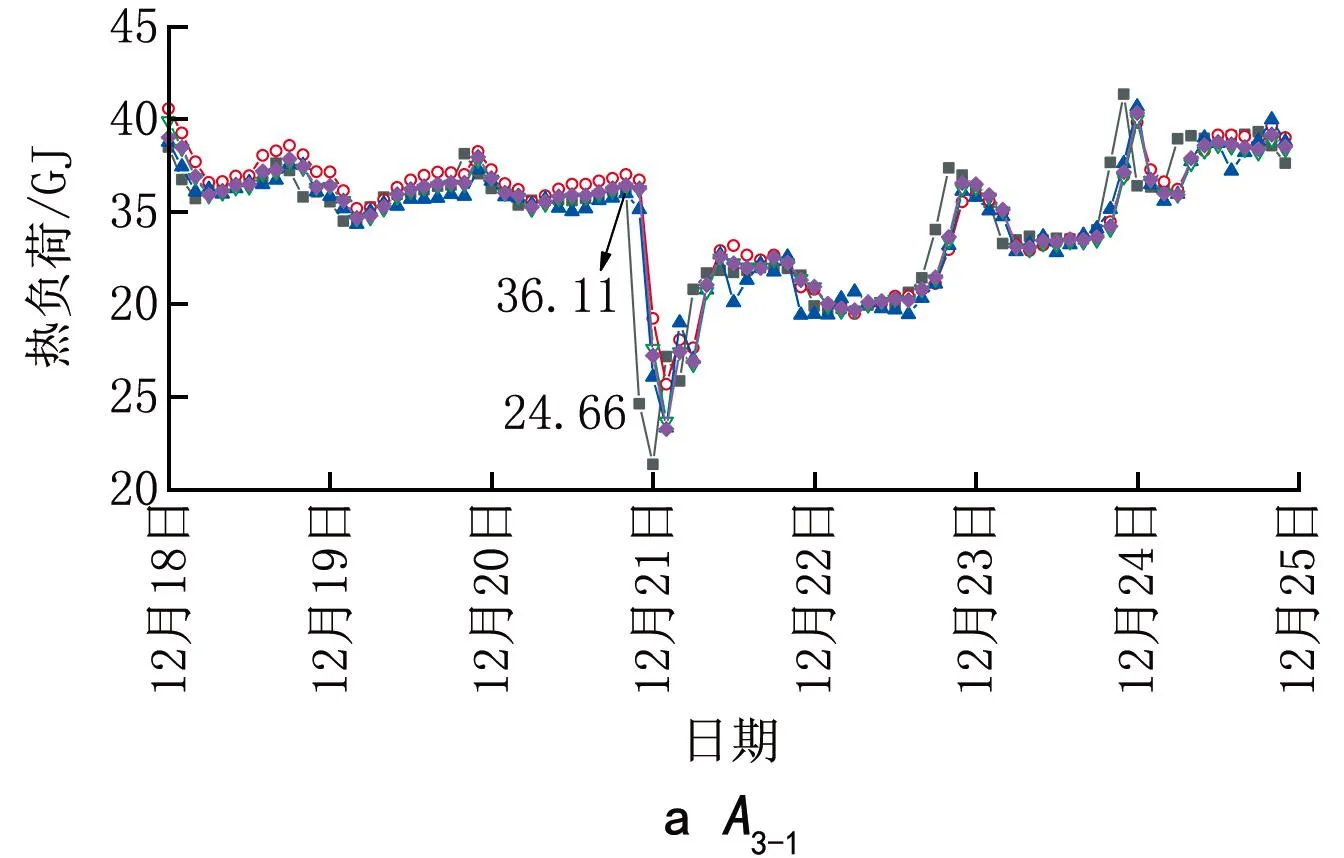
图6 4种算法在特征集A3-1和A3-2上的预测结果
4种算法在特征集A3-1和A3-2上的预测误差见表5。结合表3可知,4种算法均在特征集A3上的预测误差最大,在特征集A3-2上的预测误差最小。其中特征集A3的δmax=7.4 GJ/h,A3-2的δmax=2.3 GJ/h,即热负荷变化平稳的工况下,预测精度更高。其中,在热负荷变化剧烈时PSO-ELM的预测效果最佳,在热负荷变化平稳时PSO-ELM与PSO-SVR效果接近。

表5 4种算法在特征集A3-1和A3-2上的预测误差
2.4.3不同样本容量下的预测精度
为分析不同样本容量下算法的预测精度,以特征集A3为例,将训练集和测试集进行分割,分割情况见图7。将2018年12月25—31日期间共计84组数据固定为测试集。初始训练集为2018年11月16日至12月24日的数据,依次减少1天构成新的训练集。由于数据传输异常等原因,在部分时间内没有数据,分别从11月16日至12月15日开始一共构成了20个训练集,记为T1~T20。
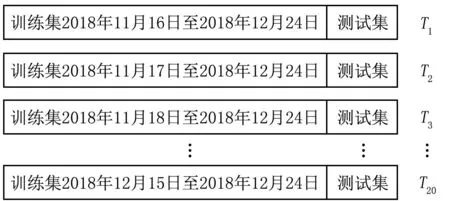
图7 训练集和测试集的分割情况
图8显示了不同样本容量下4种算法的预测误差,图中标明了各算法的最小误差。由图8可知:ELM和SVR在特征集T1~T17上的预测误差比较平稳,在特征集T18~T20上的预测误差均明显增大,对应的3个训练集数据占比分别为61%、59%和54%;PSO-SVR从特征集T18开始预测误差变大,而PSO-ELM误差变化不明显。为了进一步验证训练集数据比例对PSO-ELM算法预测精度的影响,在特征集T20基础上减去1~7 d的数据构成特征集T21~T27进行预测。由图8b可知,PSO-ELM直至特征集T27误差才明显增大,此时训练集数据占比为36%。因此,PSO-ELM可以通过更少的数据进行预测,节省预测时间。

图8 样本容量变化时4种算法的预测误差
综上,当训练集在一定范围内变化时,对预测误差的影响较小,为了缩短训练时间,可以遗忘掉前面部分数据,但是若训练集数据量过少,预测误差会增大。
3 结论
1) 对于不同特征组合下的负荷预测结果,PSO-ELM的效果均最优,其中最优特征组合为室外温度和前15个周期的历史负荷。
2) 在负荷比较稳定的工况下,PSO-ELM和PSO-SVR的预测精度均较高;而负荷波动较大的工况下,PSO-ELM的预测精度更高。
3) 样本容量在一定范围内变化对预测精度影响不大,在预测时可遗忘部分数据以节省运算时间。PSO-ELM可遗忘的数据最多,训练集占比为36%时的预测效果仍优于其他3种算法训练集占比60%的预测效果。

