沥青混凝土心墙堆石坝心墙拱效应研究

李 勇，李炎隆，温立峰，李维妹

(1.西安理工大学 省部共建西北旱区生态水利国家重点实验室，陕西 西安 710048； 2.中国电建集团昆明勘测设计研究院有限公司，云南 昆明 650051)

近年来，沥青混凝土心墙坝快速发展，为适应复杂的地形地质条件，对沥青混凝土心墙坝的设计提出了更高要求。对于具有明显分区的沥青混凝土心墙堆石坝，沥青混凝土心墙与周围壳体的刚度差异将导致不均匀沉降，甚至导致水力劈裂的发生[1-3]。因此，研究沥青混凝土心墙拱效应分布形态，合理评估心墙应力拱效应，对确保大坝安全十分必要。

沥青混凝土心墙拱效应受众多因素的影响，主要包括地质条件、材料力学特性、地形条件、心墙结构形式等。Bi 等[4]探讨了厚冰碛覆盖层基础上的高沥青混凝土心墙坝的应力和变形特性，发现沥青混凝土心墙坝存在明显的心墙拱效应，而蓄水后拱效应会明显减弱；Ghafari 等[5]采用有限元法研究参数（过渡层的弹性模量及黏土直心墙的几何结构）对施工期心墙拱效应的影响，认为当过渡层使用较软的材料及较缓的心墙坡度，能很好地缓和拱效应；Esmaeilzadeh 等[6]采用Plaxis 软件建立了55 个模型来分析泊松比、黏聚力、弹性模量、心墙斜率、心墙厚度与反滤层厚度的相关性，以参数化方法研究黏土心墙的拱效应。相较于黏土心墙，沥青混凝土心墙属于薄层结构，受河谷形状的影响大[7-8]。杨超等[9]定义河谷宽度系数以研究沥青混凝土心墙拱效应的变化规律，结果表明狭窄河谷地形会导致明显的应力拱效应；雷群华等[10]探讨了斜心墙的倾斜斜率对心墙的应力与变形的影响，结果表明无论是竣工期还是满蓄期，斜心墙竖向应力与心墙的斜率都成正比。值得注意的是现有拱效应的参数化研究以黏土心墙居多，针对沥青混凝土心墙拱效应的参数化研究明显是不全面的。

综上所述，本文首先对比直心墙、斜心墙、下直上斜式心墙拱效应的分布特征，从结构形式出发对比论述斜心墙改善拱效应的作用机制。在此基础上开展复杂地质条件下沥青混凝土心墙拱效应的定量化系统研究。选取岸坡坡度、河谷宽度、覆盖层厚度表征坝体所处的地形地质条件，分析不同地形地质条件对沥青混凝土斜心墙拱效应的影响。以期对沥青混凝土心墙堆石坝心墙拱效应有更深入的理解，并为实际工程提供参考。

1 拱效应评价方式

拱效应的大小可以用拱效应系数来描述。在本研究中，拱效应系数R定义为单元竖向应力（σZ）与单元上土条自重（γT）的比值[11]：

式中：σZ为竖向应力；γ为土体重度（kN/m3）；T为计算单元上方土体的厚度。拱效应系数越小，拱效应作用越强。若拱效应系数小于1，则表明应力正从心墙转移至过渡层及坝壳等。

当水压力大于中主应力时，心墙将产生由上游向下游扩展的竖向裂缝。通过比较有效应力法及总应力法的差异，认为应根据心墙外水压力是否超过心墙上游面处中主应力来判断水力劈裂是否发生[12]。故引入水力劈裂系数Hf：

式中：σ2为中主应力；σt为沥青抗拉强度，一般为0.2 ～ 0.4 MPa，本文取0.2 MPa；PW为静水压力。Hf≤1 表示在该作用面会发生水力劈裂。

2 数值计算模型

2.1 计算模型

参考实际工程，对坝体模型进行适当简化。沥青混凝土心墙堆石坝最大坝高98 m，坝顶宽度10 m，坝体上游坡比为1∶2.5，坝体下游坡比为1∶1.8。沥青混凝土心墙位于坝体中部，心墙底部为厚2 m、宽2.2 m 的矩形混凝土基座。沥青混凝土心墙堆石坝三维有限元计算模型见图1，计算坐标原点取在坝最大剖面底部与基座相交处，以顺河方向为x轴，以横河方向为y轴，以竖直方向为z轴。Lc为坝顶长度，u=v=w=0 b.c.表示边界条件为全约束，即在3 个方向皆不会产生位移。沿水流方向向上、下游分别延伸100 m，沿坝轴线方向向左、右岸分别延伸100 m，沿深度方向亦延伸100 m。以坝轴线长度为200 m、无覆盖层的沥青混凝土直心墙堆石坝为例，其网格单元总数为56 526，节点总数为61 609。模型全部采用六面体八节点单元（C3D8）。为合理反映心墙的力学性状，沿心墙厚度方向剖分2 层单元。在模型底部施加固定约束，在模型侧面施加法向约束。坝体施工蓄水按22 级逐级加载计算，沥青混凝土心墙与堆石材料同步升高。考虑到上游坝壳料的透水性，大坝蓄水期的水压力将直接作用在沥青混凝土心墙上。

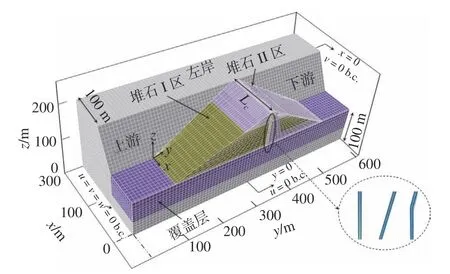
图1 沥青混凝土心墙堆石坝三维有限元模型Fig.1 Three-dimensional finite element model of an asphalt concrete core rockfill dam

2.2 计算参数

本文堆石体、过渡料及沥青混凝土心墙均采用邓肯E-B 本构模型[13-15]。材料参数由三轴试验获得（见表1）。混凝土基座及基岩都假定为线弹性材料。其中混凝土基座弹性模量为30 GPa，泊松比为0.17，密度为2.40 g/cm3；基岩弹性模量为10 GPa，泊松比为0.25，密度为2.10 g/cm3。沥青混凝土心墙与混凝土结构或堆石体之间存在强非线性接触作用。建模时，采用Goodman 无厚度单元模拟心墙与混凝土基座及过渡层与混凝土基座间接触面的受力变形，接触面参数见表2。

表1 邓肯E-B 模型参数Tab.1 Material parameters of Duncan Chang E-B model

表2 接触面参数Tab.2 Contact surface parameters

2.3 计算方案

本文进行4 组方案的计算，计算方案见图2。第1 组方案分析心墙结构形式对心墙拱效应的影响，以对比论述斜心墙改善拱效应的作用机制。通过参考大量国内外工程实例及规范要求[16]，倾斜心墙的坡度宜为1∶0.2 ～ 1∶0.4；下直上斜式心墙折坡点宜选在坝高的2/3 ～ 3/4 处。本文计算模型中，垂直式心墙顶部厚度0.6 m，底部厚度1.2 m；倾斜式心墙坡度取为1∶0.3；下直上斜式心墙在70%坝高处发生弯折，上部斜墙坡度取为1∶ 0.3。其中第2 组方案分析岸坡坡度对斜心墙拱效应的影响，坡比分别取1∶0.1、1∶0.3、1∶0.5、1∶0.7。第3 组方案分析河谷宽度对斜心墙拱效应的影响，当宽高比(Lc/H) <4 时，应考虑河谷地形对土石坝变形的影响[17-18]，即取坝长为100、200、300、400 m。第4 组方案分析覆盖层厚度对心墙拱效应的影响。统计资料表明目前80%以上已建覆盖层上土石坝覆盖层厚度均小于0.6H[19]。参考工程实际覆盖层厚度，本文覆盖层厚度分别取0、20、40、60 m。其中，H表示坝高，h表示覆盖层厚度。

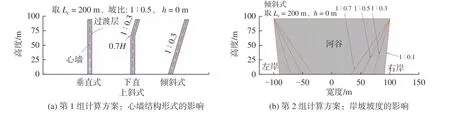
图2 计算方案Fig.2 Calculation schemes

3 计算结果分析

3.1 心墙形式对心墙拱效应的影响

图3(a)为不同心墙形式下心墙拱效应系数分布。结果表明，垂直式心墙的横向拱效应最大，下直上斜式心墙次之，倾斜式最小。这是由于斜心墙倾向上游布置时，斜心墙承受上部压应力荷载并直接传递到下游坝壳。因此，斜心墙能改善坝体受力条件，缓解拱效应。

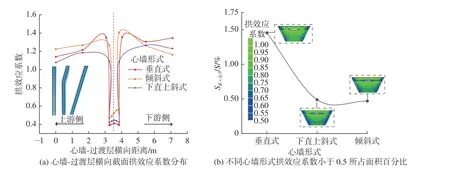
图3 不同心墙形式下心墙拱效应系数分布规律Fig.3 Distribution law of arching coefficient of core under different core configurations

有研究[20]指出，当心墙的垂直应力为相同高程下相邻坝壳垂直应力的20%～50%时，心墙可能会出现裂缝。考虑到本研究中各计算方案心墙的最小拱效应系数大于0.4，同时为保证足够的安全裕度，确定以0.5 为拱效应系数界限，求得拱效应系数低于0.5 区域的面积（SR<0.5）占整个心墙面积（S）的百分比见图3(b)。结果表明，垂直式心墙、倾斜式心墙、下直上斜式心墙拱效应系数小于0.5 相对面积所占百分比分别为1.46%、0.49%、0.47%。与之对应的水力劈裂系数分别为1.53、1.61、1.74，均大于1，说明心墙不会产生水力破坏。结合拱效应云图可以发现，应力传递的重心主要集中在心墙3H/4 附近，并且当心墙存在一定倾斜时，心墙中上部拱效应系数等值线的连续性更好，这说明斜墙较直墙能更好地缓和与周边土体的应力传递问题，这与文献[21]的结论一致。由于心墙倾向于“悬挂”在相邻的过渡带（拱起）上，致使心墙的垂直应力低于垂直上覆岩层应力。

图4 为不同心墙形式下心墙沉降变形分布。结果表明直心墙、斜心墙、下直上斜式心墙三者间拱效应差异的产生归根于心墙变形差异。由于上下游堆石区对心墙作用力的大小不同，使心墙中部变形呈现出不同的变形形态。斜心墙在坝体内整体倾斜布置，心墙整体向下游变位，有利于大坝的整体抗滑稳定。在坝顶区域，斜心墙更能适应两岸坝肩之间的不均匀沉陷，使心墙不致产生过大的应力，对改善心墙的拱效应有显著效果。规范[22]指出，根据工程实践经验，按照合理标准填筑的土石料，竣工后沉降量一般小于H/100，计算结果均符合要求。

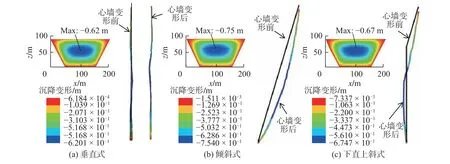
图4 不同心墙形式下心墙沉降变形分布（单位：m，变形以向上为正）Fig.4 Distribution law of settlement deformation of core under different core configurations (unit: m, positive deformation upward)

3.2 岸坡坡度对心墙拱效应的影响

图5(a)为不同岸坡坡度斜心墙拱效应系数分布。可见，岸坡坡度对心墙的应力状态有显著影响，缓岸坡能很好地缓和斜心墙与两侧土体间的应力传递现象。随着坡比的变化，最终拱起的位置从不同的角度移动到中心部分，值得注意的是在心墙和过渡层之间的边界可以观察到最大拱效应，并且在同一高程处，斜心墙上游面拱效应明显强于下游面。

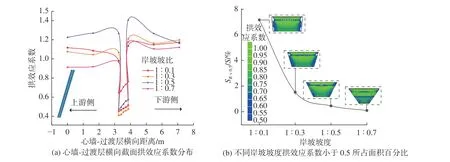
图5 不同岸坡坡度斜心墙拱效应系数分布Fig.5 Distribution law of arching coefficient of inclined core with different bank slopes

结合图5(b)可以发现，拱效应作用主要集中在心墙岸坡附近及心墙中上部，在3H/4 附近心墙拱效应最强。岸坡越陡，对应的拱效应系数小于0.5 所占的面积百分比越大，这表明心墙整体的拱效应在增强。结合拱效应系数云图可以发现坡比为1∶0.7 时，心墙的拱效应大约集中在0.5H；随着岸坡逐渐变陡，心墙拱效应强烈的区域逐渐抬升至3H/4，与此同时心墙岸坡附近的拱效应也在不断发展，由心墙两肩及两底角为起始点逐渐拓宽至整个岸坡。

为了更好地解释不同岸坡比对心墙拱效应的影响，结合心墙的剪应力做进一步阐述。图6 为不同岸坡坡度斜心墙剪应力分布，由于左右岸结果对称分布，因此只取左岸部分结果进行分析。随着河谷边坡变陡，重力在顺坡向分量F1逐渐变大，这使得两种材料接触面处由不均匀变形引起的剪应力增加，产生较大的剪切变形。而在心墙与岩体之间的剪切作用下，心墙应力传递至两岸岩体，促使心墙的竖向应力降低，产生明显的拱效应。其中剪应力的分布形态在很大程度上影响着拱效应的分布，顺坡向的剪切带会加剧岸坡附近应力传递，而剪应力的大小则会影响拱效应系数的大小。换言之，在心墙与壳体之间不均匀沉降的基础上，剧烈的剪切作用会放大拱效应。

图6 不同岸坡坡度斜心墙剪应力分布（单位：kPa，剪应力以向上为正）Fig.6 Shear stress distribution law of inclined core with different bank slopes (unit: kPa, positive shear stress upward)

3.3 河谷宽度对心墙拱效应的影响

图7(a)为不同河谷宽度下斜心墙-过渡层横向截面拱效应系数分布。V 型河谷计算模型在心墙中上部出现反拱现象，使得心墙的应力明显高于两侧过渡层。这是因为受狭窄河谷岸坡的阻挡，心墙底部在竖向应力方向上的挤压受到阻碍，使得坝体底部应力的方向发生偏转。当Lc/H为3 ～ 4 时，随着河谷宽度的增加，心墙的应力传递现象反而有所增强。这也说明单方面扩大宽高比对缓和心墙拱效应有一定的局限性。

图7 不同河谷宽度斜心墙拱效应系数分布规律Fig.7 Distribution law of arching coefficient of inclined core with different valley widths

在河谷变宽的过程中，拱效应系数云图逐渐由V 型分布过渡为水平带状分布。应力传递重心逐渐上移，由底部渐转换至心墙两岸及心墙中上部，如图7(b)所示。随着坝长的增加，应力传递经历了降低、增加、趋于稳定等3 个阶段，这说明在坝长变化过程中拱效应并非单调变化。这是由于在河谷变宽初期，坝长的增加会明显缓和河谷效应，故拱效应降低；而后虽然河谷变宽，但是自重也同时增大，使得重力沿岸坡方向的应力分量增大，剪切作用随之增大，从而使得拱效应重新增大。当坝长达到一定值后，由于坝体自重能得到很好分散，拱效应逐渐趋于稳定。

图8 为不同河谷宽度斜心墙竖向应力（S33）沿高程变化曲线。需要注意的是，相较于宽河谷，狭窄河谷（Lc=100 m）心墙竖向应力的最大值没有出现在心墙最底部，而是在心墙底部偏上，这正是心墙底部集中出现应力拱效应现象的关键。将小主应力增加到最大值时所对应的高程视为合理拱轴线高程[23]，在此高程之下的坝体均受到应力拱的影响。由此可知，窄河谷沥青混凝土心墙底部应力拱的合理拱轴线形态为单拱形，拱脚位于两岸坡脚处，在河谷轴线处合理拱轴线高度最高，约位于H/4 坝高处。以上结果表明，心墙应力分布状况受河谷地形影响显著。

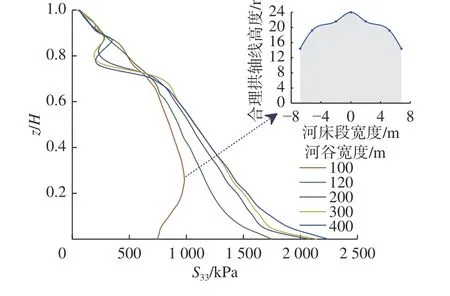
图8 不同河谷宽度斜心墙竖向应力沿高程变化曲线Fig.8 Curve of vertical stress distribution of inclined core with different valley widths along elevation

3.4 覆盖层厚度对心墙拱效应的影响

图9(a)为不同覆盖层厚度斜心墙-过渡层横向截面拱效应系数分布。覆盖层厚度增加，心墙与过渡层顺河向剖面拱效应系数随之增大，心墙中上部横向拱效应明显降低。由于覆盖层主要为河床冲积砂卵砾石层及碎石土层[24]，在堆石体作用下，覆盖层会产生较大的压缩变形，从而影响心墙沉降变形，致使心墙竖向应力出现一定程度的扩大。

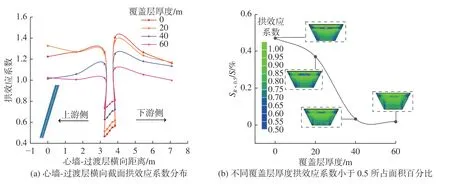
图9 不同覆盖层厚度斜心墙拱效应系数分布规律Fig.9 Distribution law of arching coefficient of inclined core with different overburden thicknesses

图9(b)为不同覆盖层厚度拱系数小于0.5 所占面积百分比曲线。结果表明，随着覆盖层厚度增加，拱系数小于0.5 所占面积百分比逐渐减小，应力传递的重心逐渐由中部转移到心墙两岸肩。心墙底部的拱效应系数值明显减小，出现众多环状分布的等值线区域且逐渐变大。这说明心墙底部拱效应变得不均匀，而不均匀的拱效应可能导致心墙底部产生局部破坏。在此期间，心墙中上部拱效应系数沿高程的分布离散性也在变大，这主要是因为覆盖层在影响心墙底部应力分布的同时，导致心墙中上部应力发生相应变化。整体而言，覆盖层对心墙拱效应的影响十分微小，拱系数小于0.5 时所占面积百分比仅变化了0.5%。换言之，覆盖层主要影响心墙底部的应力状况。

结合沉降（图10）与剪应变（图11）对覆盖层作用下的拱效应作进一步解释。覆盖层厚度增加，心墙底部变形明显增大且最大值位置逐渐降低，心墙与覆盖层之间的协调变形会使得在心墙坡脚产生较大的剪切变形。具体表现为：盖层厚度增加，心墙剪切区域增大，剪切应变由1.07%增大至1.89%，并呈现出由心墙向覆盖层移动的趋势。致使在心墙两岸底部，覆盖层与岸坡结合部位存在较大的剪应变区。心墙底部剪切带的滑移，是导致心墙底部应力传递的主要原因。心墙底部剪应变区的扩张及剪切带连续性的降低是导致拱效应等值线分布离散的关键。

图10 不同覆盖层厚度斜心墙中轴线处沉降分布Fig.10 Settlement distribution along the central axis of inclined core with different overburden thicknesses

图11 不同覆盖层厚度斜心墙横河向剪应变分布（单位：%，剪切应变以z 轴正向为正）Fig.11 Transverse shear strain distribution of inclined core with different overburden thicknesses (unit: %, shear strain is positive in z axis )

4 结 语

（1）心墙应力拱效应主要集中在心墙中部3H/4 附近及靠近岸坡处，心墙一定程度的倾斜可以改善心墙的整体受力状况。

（2）岸坡坡度变化对斜心墙应力拱效应影响显著。心墙拱效应随岸坡变陡而强烈，心墙拱效应的核心区域由0.5H逐渐抬升至3H/4，与此同时心墙岸坡附近的拱效应也在不断发展，由心墙两肩及两底角为起始点逐渐拓宽至整个岸坡。

（3）拱效应并非随河谷宽度单调变化。随着河谷变宽，应力传递的重心逐渐由底部转移到心墙两岸及心墙中上部。当坝顶长度增加到一定程度后（Lc/H达到3 ～ 4 时），斜心墙拱效应影响趋于稳定。

（4）随着覆盖层厚度的增加，斜心墙底部的拱效应系数等值线的分布逐渐集中化、区域化，并且心墙底部的拱效应明显增强，易产生局部破坏。

本文研究很大程度简化了坝体结构及实际的地形地质条件。为了更精确地模拟心墙的工作性态，未来研究有必要结合实际情况进一步分析沥青混凝土心墙的适应性和安全性。