改进的高压气枪震源气泡物理模型及其应用

赵迪, 徐润泽, 张帅, 李帅*

1 哈尔滨工程大学船舶工程学院, 哈尔滨 150001

2 浙江大学工程力学系, 杭州 310027

0 引言

地震波作为一种优质的信号能够在海洋地球物理勘探中发挥巨大的作用(林建民等, 2008).传统的震源信号如炸药等缺乏环境友好性,因而逐渐被更安全的人工震源所取代(赵明辉等, 2008).随着气枪理论的发展,高压气枪震源凭借着良好的安全性和环保性(林建民等, 2010; 吴志强等, 2016)被广泛应用于海底资源勘探(Watson et al., 2019)和地下空间结构探测(王栎等, 2022; 徐逸鹤等, 2022),目前已经成为世界上最受欢迎的人工震源.在海底结构勘探中,当震源气枪在水下发射后,数十兆帕的压缩空气在短时间内从气枪内释放至水中,形成高压震源气泡(最大半径为米级),震源气泡剧烈脉动激发的压力波会在海底不同媒质分界面发生反射,通过解析反射波信号即可探查海底资源分布情况(Zhang et al., 2021).由于高压震源气枪气泡脉动产生的压力波信号是宽频信号波(Chelminski et al., 2019),其中低频成分穿透能力较强(赵明辉等, 2008),成像效果较好,而高频成分不仅会快速衰减和散射(林建民等, 2008),还会对海洋生物造成严重的噪声污染(Watson et al., 2019).因此为了改善震源气枪的性能,需要对其背后的高压气枪震源气泡非线性动力学进行研究.

在气枪震源气泡动力学理论的发展历程中,Ziolkowski(1970)基于Gilmore方程建立了首个气枪气泡动力学模型,并用实验数据进行了气泡初始条件的修正,由于忽略了气体从腔室注入气泡的动态过程,该模型过高的估计了压力波的首脉冲.Landrø(1992)在其气泡初生模型中假设枪体内的气体匀速向外释放,且高压腔室内的气体温度始终为环境温度.由于该模型存在不合理的物理假设,需要调节多个人工参数.其后,许多沿用该方法的气枪震源气泡初生模型(Li et al., 2011; Watson et al., 2019)均导致震源压力首脉冲的计算精度不如人意.Schulze-Gatterman(1972)将气枪枪体视为球泡内的刚性球体,建立了气枪信号能量、频率以及气泡脉动幅值的理论解.Landrø和Langhammer(1993a,b)在模型中引入了热力学开放系统,探究了温度对气枪震源信号的影响,他们还发现黏性并不是震源气泡脉动过程中能量损失的主要因素.Li等(2011)探究了热传导、枪口节流以及气泡上浮对震源气泡动力学的影响.de Graaf等(2014b)综合了黏性、热传导、枪体、蒸发冷凝等多个因素对气枪震源气泡压力场进行了模拟.Watson等(2019)总结气枪工作压力是影响压力波首脉冲的首要因素,低频成分取决于工作压力和腔室容积.张国平等(2019)引入多个对模拟结果具有重要影响的修正因子来改善传统的单枪压力子波计算方法,其计算精度相比前人的模型有明显提高.此外,气枪震源在真实作业过程中被工作船以恒定的速度拖行(2 m·s-1及以上),震源气泡初生时会携带一定的水平初速度,但是该因素对震源气泡后续运动及压力波的影响规律尚未揭示.因此为了更真实的反应高压气枪震源气泡在海底勘探时的物理特性,还需结合气泡的平移运动进行研究.

在对多枪震源的研究中,Ziolkowski等(1982)提出了气枪阵列中点源气泡相互作用理论并研究了气枪阵列中复杂的相干关系.Li等(2011)建立了气枪阵气泡群线性耦合理论模型,探讨了不同容积气枪气泡在耦合过程中的“频率锁定”现象.叶亚龙等(2015)对Ziolkowski等提出的模型进行了修正,并考虑热力学效应,研究了平面气枪阵列的远场压力波特性.Zhang等(2017,2019)研究了气枪阵列的优化问题,并对气枪阵列中气枪间距和体积对压力波的影响进行探讨.Zhang等(2023)建立了气泡统一方程,可同时考虑流场边界、多气泡耦合、流体可压缩性、表面张力、黏性等诸多因素影响,在气枪震源领域有很好的应用前景.在多枪震源的基础上,非同步多枪技术既能够降低气泡脉动固有频率(增强压力波低频能量),还可以控制双枪激发时间以削弱首脉冲高频成分,该方法的应用可以有效改善气枪震源在深海勘探时的性能.为此本文将针对非同步双枪气泡耦合作用及其压力波频谱特性开展理论研究.

针对前人研究的不足,本文针对气枪震源所涉及的前沿问题开展基础性研究.首先,建立解析的计及物质输运效应和流场可压缩性的气枪震源气泡初生模型,解决气枪首脉冲精确计算难题;在气枪线性开口假设模型的基础上(Li et al., 2020),对气枪的多种开口方式进行深入探讨并分析该因素对首脉冲的影响规律.此后,探究水平移动速度对震源气泡动力学特性及远场压力的影响,并给出可以忽略气泡初始平移速度的临界条件.最后,建立非同步双枪气泡耦合模型,并从理论角度探索双枪发射的时间差对震源压力波谱的改善效果.本文工作旨在为气枪震源气泡动力学的研究及海底资源勘探领域提供参考.

1 改进的气枪震源气泡动力学理论模型

1.1 可压缩流场中气泡动力学基本理论

(1)

式中,c是液体中的声速(1500 m·s-1);ρ是液体的密度(1000 kg·m-3);R是气泡的半径;最后一部分压力项Δp的展开形式为

(2)

式中,pb是气泡内部气体压力,pv是液体的饱和蒸汽压力,σ是表面张力系数,μ是动力黏性系数,pimage是自由液面上方镜像虚拟气泡产生的声压,通过这一项来考虑自由液面效应.在雷诺数和韦伯数都较大的条件下,可以忽略黏性和表面张力的影响(艾旭鹏和倪宝玉, 2017;Han et al., 2002;Li et al., 2024).同时饱和蒸汽压力也并不是影响气枪气泡动力学的主要因素,因此在模拟时可以忽略这三个因素.结合伯努利方程,可以得到震源气泡周围近场压力的表达式为

(3)

(4)

式中,r为气泡中心与远场测点的距离,V为气泡体积.实际上方程(3)中第二项展开后含有r-4项,当测点足够远时方程(3)和(4)是等价的.本文用方程(3)来计算近场压力,用方程(4)计算远场压力.

1.2 震源气泡平移运动对气泡动力学方程的修正

经典气泡动力学中基于小体积气泡的研究忽略了气泡平移速度ub对流场的影响(Hsiao et al., 2003).实际上在海底勘探时高压震源气枪产生的气泡半径接近1 m数量级,当震源气泡有平移运动时,有必要考虑其速度对方程中压力项的修正(Hsiao et al., 2003; Zhang et al., 2023)：

(5)

式中,u代表流体的运动速度.考虑气枪震源气泡产生后在二维流动液体中的受力,气泡的运动方程可以写为(Ohl et al., 2003)：

(6)

等号右边分别代表了浮力、拖曳力、包含附加质量的压力梯度、液体虚附加质量变化的影响.拖曳力项中拖曳力系数的经验表达式为(Hsiao et al., 2003)：

式中雷诺数Re的表达式为

(8)

(9)

1.3 多气泡耦合模型

实际上单个气枪震源往往难以满足海底地质勘探的要求,气枪通常是以多枪阵列的形式进行工作.因此为了探究气枪震源气泡间相互作用对压力波以及频谱的影响,需要建立多气泡耦合模型.

气泡之间的相互作用可分为强耦合作用和弱耦合作用.在强耦合作用下,气泡会失去球状特征并互相挤压最终发生融合(Bremond et al., 2006).在弱耦合作用下,气泡相干性使气泡脉动发生变化,进而对压力波和频谱造成影响.在探测海底的背景下,震源气泡之间的弱耦合作用占主导,因此本文仅讨论气泡之间弱相互耦合作用的影响.根据气泡周围流场环境压力修正的观点,Pelekasis等(2004)给出了不可压缩条件下多气泡的R-P方程的修正形式.同样在可压缩条件下,多气泡耦合动力学方程可以表示为

(10)

式子中下标用来区分气泡,L是两气泡之间的距离.Bremond等(2006)通过实验证实了虽然气泡发生了微小变形,但用该方法来模拟气泡间相互作用是简单又可行的.从表达式中也能够发现,当距离L趋于无穷大时,该修正项趋近于0,气泡间相互作用可以不计.

1.4 气枪与气泡系统物质输运模型

建立气枪震源气泡物理模型的关键在于对气枪气泡系统物质输运过程进行合理的模拟.对于气枪震源气泡或者水下爆炸型气泡来说,气泡的初生状态为高压小体积球泡(de Graaf et al., 2014b).因此本文将气泡的初始体积设置为气枪体积的百分之一,初始压力设置为静水压,气枪和气泡的初始温度均为环境温度(Li et al., 2020).气枪发射后,假设气体从腔室向气泡内的运输是等熵过程,当阻塞流(气体流经枪口的速度达到声速)条件成立时(Chelminski et al., 2019)：

(11)

气体质量变化遵循下式(Li et al., 2020)：

(12)

当该条件(11)不满足时(de Graaf et al., 2014b)：

式中Pg,Pb分别表示气枪和气泡的压强,Mg,Mb分别表示气枪和气泡内部气体的质量.Vg代表腔室的容积,γ是绝热常数,Sport是每一时刻下枪口面积.在de Graaf传统理论模型中,由于直接采用最大开口面积进行计算而没有考虑放气过程中开口面积的变化,导致模拟的首脉冲峰值远大于测量值(de Graaf et al., 2014b).本研究采用了Li等(2020)提出的线性开口假设,该开口方式对于震源气泡产生压力波的首脉冲幅值和斜率的模拟较为准确,Sport随时间的变化如下所示：

(14)

这里Topen是气枪开口的时间,Tclose是开口关闭的时间,当腔室内气体残留5%时,枪口瞬间关闭.

由于气体释放过程中气泡与外界之间发生能量和物质的交换,所以需要利用热力学开口系统来分析.本文主要考虑气体内能的影响并忽略气体在水中的耗散,对热力学开口系统能量方程求时间导数后整理得到气泡温度变化率表达式：

(15)

式子中Tg,Tb分别指气枪和气泡内部的温度,Vb是气泡的体积,Cv和Cp分别是等容比热容和等压比热容：

(16)

Cp=Cv+R,

(17)

(18)

式中,Tw是环境中液体的温度,Sb=πR2是气泡表面积,k是传热系数,通常取为2000～8000 W·m-2K.

气枪内部物理量可通过气泡的物理量来更新：

(19)

(20)

最后气泡和气枪内部气体的压强可通过理想气体状态方程得到：

PV=MRT.

(21)

在上述关于震源气泡动力学以及气枪气泡系统物质运输方程的基础上,我们通过自主编写程序,在自适应时间步长(Wang et al., 1996)下,采用四阶龙格库塔法可得到震源气泡半径的数值解,进而求得震源压力波及相应的频谱曲线.

2 理论值与实验值对比验证

本节中为了验证所建立的高压气枪震源气泡物理模型的正确性,将该改进模型得到的压力波理论值与de Graaf用传统理论模型得到的结果(de Graaf et al., 2014b)以及澳大利亚国防科学技术组织利用SERCEL520型气枪测得的实验值进行对比.根据文献中的工况设置,将气枪工作压力分别为20.7 MPa(3000psi)和17.2 MPa(2500psi),气枪沉放深度分别为3 m和5 m.其他参数均保持一致,其中气枪腔室容积是8521 cm3(520in3),枪口最大面积为128 cm2.测点位置位于相同深度下距离气枪2.22 m的位置.绝热常数γ设置为1.4,考虑震源气泡在水中脉动时表面Rayleigh-Taylor不稳定性的发展会增加传热,将传热系数k设置为7000 W·m-2K(de Graaf et al., 2014a,b).由于气枪开口时间Topen的大小至今没有确切的设置方式,在本研究中通过测试发现将Topen设置为3.5 ms得到的结果与实验值最为符合.

图1中所展示的压力波曲线均为叠加自由面虚反射(虚反射系数为-1)后的结果,且两工况下均考虑了气泡上浮的影响.图1a中显示,实验测得的压力波曲线(黑色四边形表示)在2.5 ms左右时达到峰值,之后在虚反射作用下,压力波值迅速下降.在0.02 s左右时曲线出现了波动,这是由于从固壁处反射回的压力波引起的(de Graaf et al., 2014b).通过对比可以发现,改进的模型对首脉冲模拟的结果(粉色实线曲线)仅小于实验数据3.8%,而传统模型(蓝色点线)要超出实验数据约35%.这表明不考虑气枪的开口过程将会极大高估压力波首脉冲.此外从图1a中明显看出改进的高压气枪震源气泡物理模型对气泡脉冲的模拟结果也要优于传统模型.图1b中展示了第二个工况下各个模型得到的结果.同样改进模型得到的首脉冲峰值仅比实验数据小0.24%,周期仅长5.3%,而传统模型的误差则分别为39.0%和8.1%.再次证明了本研究中所建立的改进的气枪气泡物理模型更加合理有效.

图1 实验数据与传统模型和当前改进模型的对比 (附图为首脉冲局部放大图)(a) 工况1; (b) 工况2.

本研究中改进的物理模型较传统模型得到了显著改善,但是仍存在一定的误差.虽然两次对首脉冲峰值大小的模拟都与实验数据符合良好,但峰值到达时刻的预测却与实验数据存在显著差异,这可能是由于开口方式的选取不够合理所造成,后面的章节中将对该问题进行进一步的讨论.对于两工况下周期预测值均偏小,这可能与气泡形成的过程有关.SERCEL型气枪发射是从四个端口同时释放气体(de Graaf et al., 2014b),在气泡脉动的第一个周期内四个小气泡并没有完全融合为一个完整的大气泡,气泡间的相互作用会使气泡周期略有延长.

3 结果与讨论

高压气枪震源气泡脉动特性及流场压力波受气枪特征参数、气泡初始条件、气泡相互作用等多因素的影响.为了探究不同影响因素对高压气枪震源气泡动力学的影响规律,本节将针对气枪腔室容积、气枪工作压力、气泡平移速度、气枪开口方式、气泡间距以及气枪非同步激发进行讨论.

3.1 气枪腔室容积的影响

气枪腔室容积对所产生的震源气泡半径和压力波影响显著,图2展示了利用工况1中的参数模拟水下10 m处不同体积气枪发射得到的半径和压力波结果.对比图2a中的曲线可以发现随着枪室容积的增大,气泡半径显著增加.520 in3气枪激发所产生气泡的最大半径较150 in3增大49.3%.这是由于气枪容积直接决定了气枪放出气体的总质量,容积越大,释放的气体就越多因而能够产生更大的气泡.图2a的插图中显示,气泡的最大半径随腔室体积的立方根成线性变化,这与理论研究结果是一致的.近场压力波随气枪腔室容积变化的结果如图2b所示,首脉冲和气泡脉冲的幅值都会随腔室容积的增大而增大.特别地,子波周期随容积的变化最为显著.当容积增加到520 in3时,周期增加了约50.6%.Nooteboom(1978)在研究中指出在气枪震源工作压力和深度不变的情况下,周期正比于腔室容积的立方根：

图2 气枪腔室容积的影响(a) 气泡半径; (b) 1 m处近场压力.

(22)

这与图2b插图中展示的结果也是一致的.

3.2 气枪工作压力的影响

气枪工作压力也是影响气枪震源气泡脉动特性的关键因素,图3展示了改变工作压力后得到气体质量变化率、气泡半径、远场压力、压力波频谱的结果,参数设置与上一节相同,测点位于远场100 m处.从图3a中可以看出,随着工作压力的增加,气体质量变化率显著提高.相同时间下喷出气体质量增多导致气泡的半径明显变大.图3b的插图中显示气泡的最大半径与气枪的工作压力接近正比关系,但由于气枪压强较低时气泡可能无法顺利膨胀,故在低压下曲线斜率会产生偏差.气枪工作压力也是影响首脉冲的关键因素,从图3c中可以看出首脉冲峰值随着工作压力的增加增大了54.2%,这是由于气泡膨胀更剧烈造成的.由于气泡体积的增大会使得气泡脉动的周期延长,固有频率降低;首脉冲增大又会使得高频成分增加.因此在图3d的频谱曲线中,虽然主频从9.4 Hz下降至了约7.4 Hz,声压级大小增加了1.1%,但由于高频段声压级也增加了约2%,因此采取增加气枪工作压力的方式不能满足新型绿色气枪震源的要求.

图3 气枪工作压力的影响(a) 气体质量变化率; (b) 气泡半径; (c) 远场压力波; (d) 压力波频谱.

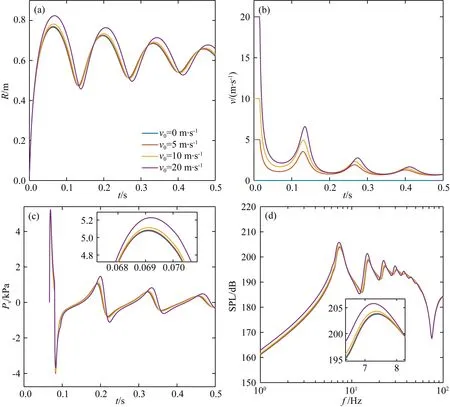
图4 气泡平移速度的影响(a) 气泡半径; (b) 气泡水平平移速度; (c) 远场压力; (d) 压力波频谱.

3.3 气泡平移初速度的影响

由于在工程中气枪震源常常是由震源船拖曳工作的,因此震源气泡在水中产生的同时还拥有与气枪移动速度相同的水平初速度.图4展示了水平初速度大小对气枪气泡动力学特性的影响,参数设置与上节相同.在修正的气泡动力学方程中,速度平方项的存在相当于将环境中静水压减小了ρu2/4,因此外界对气泡脉动的抑制作用会有所削弱.在图4a和图4c中可以看出,当v0为5 m·s-1和10 m·s-1时,气泡半径和压力波首脉冲略有增大.当v0=10 m·s-1时,气泡半径、周期以及首脉冲峰值分别仅增加了2.1%、2.0%和0.7%,当v0=20 m·s-1时才能产生明显改变.通过图4b分析气泡速度变化发现,气泡平移速度是呈周期性减小的.初始时刻由于气泡迅速膨胀,其平移速度在阻尼力和附加质量力作用下迅速减小为一个小值.此后随着气泡收缩,附加质量力符号改变,加速度变为正值,气泡的平移速度又开始逐渐增大.但由于气泡脉动的幅值会随能量消耗逐渐减小,因而速度变化的幅值也随之减小.在阻尼力的作用下,气泡移动速度最终趋于0.

由于气泡的平移速度仅仅在产生初期时才保持为较大值,因此其对气泡脉动特性以及压力波的影响十分微弱.本文发现当气泡初始平移速度v0的值为7 m·s-1和16 m·s-1时,气泡半径和周期分别会增加1%和5%.此外在图4d压力波频谱曲线中,即使v0=20 m·s-1,主频和其对应的声压级大小也只产生约2%和1%的变化.实际上用于海底勘探的拖船工作航速通常在6 kn左右,该速度远小于上述临界值,因此在工程研究中可以不考虑该参数的影响.

3.4 气枪开口方式的影响

第二节中采用了线性开口假设(Li et al., 2020)模拟了气枪震源的放气过程,该方法对首脉冲到达时刻的预测晚于实验测量值61.4%.为了降低该误差,本节将开口函数统一设置为幂函数,开口时间统一设置为3.5 ms,通过调节幂指数的大小来改变开口的方式,其他设置同第二节中工况一相同.图5a中显示,随着幂指数的增加,峰值到达的时刻逐渐后移,同时幅值也逐渐减小.但由于开口时间极短,因而气泡脉冲并没有产生明显变化.通过与实验数据对比,发现当指数为0.7时,压力波首脉冲值大于测量值1.5%,到达时刻晚于测量值17.3%,此时模拟的准确度优于线性假设.而指数为1.3时,误差均超过了线性假设.但是若从首脉冲斜率与实验值的对比中来看,线性假设的结果似乎更为符合,因此不能片面地评判哪一种开口形式是最佳的.由于气枪开口形式与气枪内部结构中梭阀的运动密切相关,为了更准确的模拟气枪发射过程,还需要结合放气时间对梭阀的运动方程进行进一步的研究.

3.5 双枪间距对双泡耦合作用的影响

实际在海底勘探工程中往往会把多只气枪按照一定方式组合在一起形成气枪阵列,利用气泡之间的相互作用来提高气枪震源工作的性能.气泡间距是影响气泡相互作用的重要参数,这里为了方便研究忽略气泡上浮效应.对应图中设定的距离,用Rmax表示分别为2.11Rmax,3.20Rmax,4.29Rmax,5.38Rmax.从图6a可以看出,与两个孤立气泡得到的结果相比,随着气泡间距的减小,压力波首脉冲峰值逐渐降低,周期延长,这表明气泡的脉动受到了抑制.尤其当距离缩短到L≈2.11Rmax(l=2 m)时影响最为显著,此时峰值减小了6.6%,周期增加了18.1%.对应于周期的变化,在图6b中也可以看出随着L的减小,主频明显向左移动.在L≈2.11Rmax(l=2 m)时主频减小了约18%,而声压级大小仅降低了1.1%.因此工程中可以采用双枪耦合的方式来降低气泡脉动的固有频率,使频谱的低频性能得到改善.

图5 气枪开口方式的影响(a) 近场压力; (b) 压力波频谱.

图6 双枪间距对双泡耦合作用的影响(a) 远场压力波; (b) 压力波频谱.

图7 双枪延迟时间对双泡耦合作用的影响(a) 气泡1的半径; (b) 远场压力; (c) 压力波频谱.

3.6 双枪延迟时间对双泡耦合作用的影响

高压气枪震源信号的高频段与其产生的压力波首脉冲密切相关.从HSE(Health、Safety、Environmental)的角度考虑,为了减小高压气枪用于海底勘探时产生的高频段信号对海洋生物的影响,我们希望通过气枪延迟发射的方式使两个首脉冲压力波实现部分抵消.图7展示了本文针对气枪延迟时间研究得到的结果.图7a中显示随着两枪延迟时间的增加,首发气泡的最大半径略有减小.当Tdelay=6 ms时,气泡最大半径仅减小了3.7%,这可能是由于气泡间相互作用延迟造成抑制作用时间减小导致的.在图7b中可以看出,当Tdelay小于3 ms时,随着Tdelay的增加,首脉冲形成的时间在后移,且幅值也减小了12.5%.Chelminski等(2019)在研究中指出由于震源压力波首脉冲曲线的斜率与对海洋生物的影响成正相关,该斜率越大,高频成分越多,其危害作用越大.因此可以通过控制气枪发射时间差来使首脉冲上升的时间尽量延长以减小其对生态的不良影响.但是当Tdelay进一步增大后,由于双泡产生的压力首脉冲峰值明显错开,形成了两个单独的峰值.对于气泡脉冲来说,时间延迟似乎并没有产生明显影响.反映在图7c的频谱中,可以发现气枪的非同步发射能够在保证信号低频段不变的情况下,有效的降低高频段的能量.

此外需要注意,受自由面虚反射的影响,反射波到达的时间大致为2H/c.因此理论上频谱中的陷波点应该在频率为c/2H的位置处(Zhang et al., 2018).但是当Tdelay大于3 ms时,由于时间延迟导致虚反射到达时间延长,频谱中第一个陷波点出现的频率明显左移.当延迟6 ms发射时,陷波发生的频率减小了66.5%,这将严重缩短频谱的有效宽度.因此在采用该方法改善高压气枪震源的实际工作时,要综合考虑压力波首脉冲以及陷波点两方面影响.

4 结论

本文基于高压气枪震源气泡在海底勘探中的实际应用,在引入了气枪气泡系统之间的物质输运效应、气液热传导等影响因素后,建立了改进的高压气枪震源气泡物理模型.该模型通过与实验数据和传统模型对比后验证了其正确性和理论完备性.在此基础上我们利用该模型对高压气枪震源气泡动力学及震源压力波的影响因素进行了参数化研究,得到的结论如下：

(1)高压气枪震源气泡的最大半径和周期都与气枪腔室容积的立方根呈正比关系,与气枪工作压力也近似呈正比关系(工作压力较小时有一定偏差).单独提高气枪工作压力会同时提高压力波低频和高频能量,因此不能满足新型绿色气枪震源的要求.

(2)高压气枪震源气泡水平初速度对后续气泡运动及压力波的影响不显著,当v0=7 m·s-1,气泡半径和周期较v0=0 m·s-1工况仅增加1%.

(3)气枪开口方式对震源压力波首脉冲影响显著.当用幂函数s=ktα表示开口过程时,α=0.7时对峰值点的模拟效果最好,α=1时(即线性假设)对首脉冲曲线上升段模拟效果最好,更准确的开口方式还需进一步探究.

(4)气枪气泡间的相互作用有利于降低气泡脉动的固有频率,并且随着气枪间距的减小相互作用增强,当距离缩短至约2.11Rmax主频可降低约18%,此时影响效果最为显著.

(5)采用气枪非同步发射的方式可以在保证震源压力波信号低频段不变的条件下,使高频段能量有一定程度得降低.但当延迟时间超过一定数值时,陷波点的大幅前移会使频谱的有效宽度减小.