基于区间型数据离散化算法的电力应急物资供应质量可追溯模型研究

王民涛,陈立钊

(1.国网内蒙古东部电力有限公司,内蒙古 呼和浩特 010090)

(2.国网赤峰供电公司,内蒙古 赤峰 024099)

电力应急物资的供应由于受到技术与成本等因素的限制[1-2],导致物资的质量追溯较为困难,且每个环节中所使用的溯源技术有所不同,因此溯源技术的优势未能体现出来,限制了此技术的发展与应用。

电力是保障人民生计的能源系统之一。电力应急物资的质量反映了一个国家对人民生计的重视程度。然而,电力应急物资供应链在应用过程中受到各种限制,且可追溯性较差[3]。针对此情况,本文提出一种基于区间型数据离散化算法的电力应急物资供应质量可追溯模型,应用此模型对所有物资信息进行详细记录,当供应质量发生问题时,能够在最短的时间内找到问题的根源,对其进行改进。

1 应急物资质量可追溯模型构建思路

不同的对象其追溯模型具有不同的特征,一是应急物资储备数量上的不足,二是对应急物资储备的管理不到位,在使用数学模型进行应急物资质量可追溯性分析时,有一定的难度。为此,本文使用半定量、半定性技术[4]对其进行分析。在确定追溯主体与追溯客体后,将整体追溯模型的运行过程分为7个环节,如图1所示。

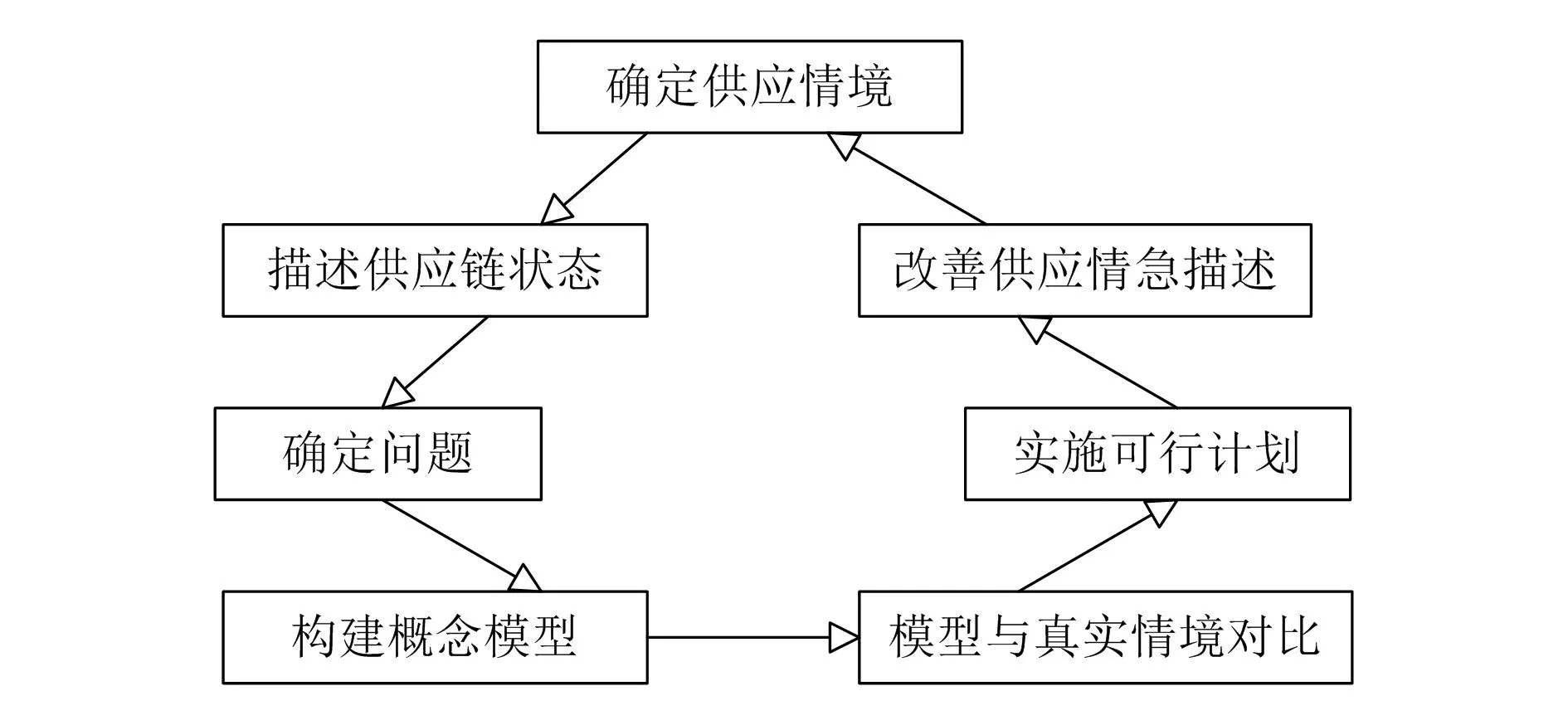
图1 供应质量追溯思路

部分物资标识并不具备唯一性,不同批次物资的标识均有所不同,为了获取可靠性更高的追溯结果,本文采用区间型数据离散算法构建新型追溯模型。区间型数据离散算法的计算过程为:

(1)

式中:S*为离散处理后的数据,S为模型计算中采集的原始数据,Smax为模型计算中采集到的原始数据最大值,χ为离散计算系数,I为样本数量,Si为第i个样本的值。

2 电力应急物资供应质量可追溯模型构建

2.1 电力应急物资供应质量关系分析

在电力应急物资供应过程中,为了尽可能地捕捉到与质量相关的信息,需要建立一个制度,对各个供应环节的信息进行跟踪和追溯。这个制度将以电力应急物资供应周期的形式呈现,以为后续追溯工作提供分析基础和支持。电力应急物资供应周期如图2所示。

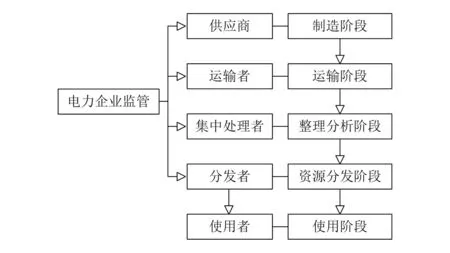
图2 电力应急物资供应周期

在质量因素中,一部分可以通过测量获得,用具体数值表示,例如温度、质量、尺寸等,将其称为质量定量因素,用Ac表示;另一部分不能通过测量仪器测定,只能通过人的感官进行判定,例如外观质量、气味、口感等,在本文中将其称为质量定性因素[5-6],用Ad表示。为了获得更加真实的分析结果,对定量因素和定性因素进一步细分,在构建追溯函数时,考虑到偶然发生事件α和各指标的理论赋值β,可以更全面地考虑和评估各种因素对应急物资质量指标的影响。再通过将Ac、Ad与α和β进行组合,可以得到更准确和真实的应急物资质量指标取值结果。应急物资质量指标理论值由上述几个因素共同决定,则有:

β=f(Ac,Ad,α)

(2)

式中:f(·)为追溯函数。

要保证物资供应质量,需要在物资生产后对其进行检测,剔除不合格产品,但此种方式不能改变β的分布情况,且会增加追溯的工作量,因此需要构建多质量因素追踪函数。为便于后续的计算,将其设定为线性正态函数。假设在供应链中存在n个影响供应质量的因素q1,q2,…,qn,在评估和控制物资质量时,需要关注的指标有o个,分别为α1,α2,…,αo,o1表示定量指标,o2表示定性指标:

o1+o2=o

(3)

则影响供应质量的因素与需要关注的指标之间的线性关系可表示为:

(4)

式中:x为物资所在供应环节序号,e、d分别为函数中的计算常数以及计算参数。由于此线性关系函数涵盖了大量的数据,为了降低计算难度,将其整合为矩阵的形式,则有:

(5)

式中:Q为需要关注的指标向量,E为计算向量常数,D为影响供应质量因素与需要关注的指标之间的系数矩阵,X为影响供应质量因素的值矩阵,D1为定量因素的系数,D2为定性因素的系数。

根据式(5)确定电力应急物资供应质量指标之间的关系,并使用其对采集到的指标进行分析,以明确指标内容和其对应的影响因素,将其作为模型搭建的基础。

2.2 应急物资供应链时间参数计算

需要对供应链周期进行计算,以此确定出现质量问题的环节。本文将时间参数的计算公式设定如下:

time=timei+timej+timek

(6)

式中:time为质量问题的输出时间,timei为质量问题的输入时间,timej为质量问题的等待处理时间,timek为质量问题的处理时间。由于应急物资供应环节存在并行行为,则式(6)应转化为:

(7)

式中:m为供应环节中并行结构的数量。结合电力应急物资供应过程中的实际情况,在应急物资供应链的每个环节,包括质量问题的输出、输入、等待处理和处理时间,会受到一定程度的随机性影响。假设供应链中的各个环节在时间处理上是均衡的,那么供应链中每项业务的总运行时间timeall可表示为:

(8)

根据式(8)计算供应链各环节的处理时间,并将其相加作为总运行时间的一部分。这些处理时间可以是确定性的值,也可以是以随机变量的形式表示的值,并作为追溯过程中的时间系数。通过将时间参数设定为随机变量,可以更准确地模拟供应链的运行情况,并考虑到潜在的风险和不确定因素,更好地理解和预测供应链的性能。则式(8)应转化为:

(9)

将式(9)计算结果导入仿真软件中,同时将应急物资供应链代入其中,得到供应链的总运行时间,为后续的计算奠定基础。

2.3 构建区间型数据离散化物资质量可追溯模型

应用区间型数据离散算法中的计算公式(1)对原始数据进行处理和分析,以构建符合应急物资质量追溯要求的模型。在本文中,将模型设定为原始物资W1、运输中物资W2以及应用中物资W3三部分,其中原始物资阶段指应急物资供应链中的初始阶段,即从物资的生产或采购开始,到进入运输环节之前的阶段。在该阶段,涉及X批次的原始物资,即尚未进行运输和应用的物资。运输中物资阶段指应急物资供应链中的运输阶段,即原始物资从供应商处运输至应急物资储备库或者其他目的地的阶段。在该阶段,G批次的应急物资处于运输过程中,会面临一些因运输而引起的质量问题。应用中物资阶段指应急物资供应链中的最后阶段,即运输结束后物资进入实际应用环节的阶段。在该阶段,Z批次的应用中物资已经运输到位,进行实际的应急使用或分发,会面临一些与应用相关的质量问题。则此时供应过程可表示为:

W1={W1,1,…,W1,i,…,W1,X}

(10)

W2={W2,1,…,W2,i,…,W2,G}

(11)

W3={W3,1,…,W3,i,…,W3,Z}

(12)

式中:W1,X、W2,G、W3,Z分别为不同分布阶段X批次的原始物资供应集、G批次的运输中物资供应集、Z批次的应用中物资供应集。

不同阶段的可应用率,即应急物资在供应链中各个阶段中的合格或可用物资的比例,其计算公式为:

(13)

式中:h(a,b)为第a个问题物资与第b个正常物资之比,问题物资的数量为A,正常物资的数量为B。通过该比例可确定目标物资需要追溯的比例[7-8]。将式(13)结合时间参数对应急物资进行追溯,可得到异常质量区间以及物资区间属性η。假设此属性在区间中的不一致率阈值为∂,将此区间等分为U簇。对于两个相邻的供应周期,其不一致率[9]分别为δi与δi+1,对应的簇分别为Ri与Ri+1,此时,两簇之间的不一致率可表示为:

(14)

式中:QRi∪Ri+1为Ri簇与Ri+1簇并集的不一致率阈值。

不一致率可以评估应急物资供应链中不同阶段的物资质量的差异或变化。当不一致率相对稳定地递增时,即表示供应周期内的物资质量基本保持一致。但如果出现δi≤δi+1且δi+1≤δmax的情况,说明两个相邻的供应周期Ri与Ri+1之间发生了质量问题,存在一个断点,此时的Ri与Ri+1的数值即为应急物资质量问题追溯点。因此,通过观察不一致率的变化趋势并检测断点,可以确定应急物资供应链中存在的质量问题,并追溯到问题的具体时间点(即断点)。

至此,基于区间型数据离散化算法的电力应急物资供应质量可追溯模型构建完成。

3 仿真分析

3.1 仿真实验准备

本文构建了仿真实验平台对文中构建模型的使用效果进行分析,采用ExSpect仿真软件完成电力应急物资供应环节的仿真。在物资供应业务中,由于各种因素的影响,每个具体操作的完成时间往往是不确定的,具有一定的随机性。为了使仿真结果更加贴近真实数据,假设各项业务完成的时间服从某种分布,具有均匀性。部分关键参数见表1。将参数导入ExSpect仿真软件中,对电力应急物资供应环节进行仿真,完成了用于模拟电力应急物资供应环节的运作过程的仿真环境构建。

表1 电力应急物资供应环节部分关键参数

3.2 仿真场景设计

将变压器作为进行电力应急物资供应质量验证实验对象产品,结合某城市电力应急处理环境,采用历史数据构建溯源模型。模型验证条件设定如下:

1)对供应链中的变压器生产批次进行ID编号,每个批次号都对应着一组变压器,而不同批次号的变压器质量和性能均会有所差异。通过为每个变压器批次分配唯一的ID,并进行批次号识别,可以帮助在供应链中的监管部门或用户更好地追溯和记录变压器的质量信息。因此,将变压器的批次号(XT-1、XT-2等)作为唯一标识用以辨别变压器的质量。在模型验证中,根据批次号和其他相关数据,对变压器的质量进行评估和验证。根据现行的产品追溯码编码规则进行设计,对供应链中的数据进行统计与计算,得到相应的数据整理成表2。

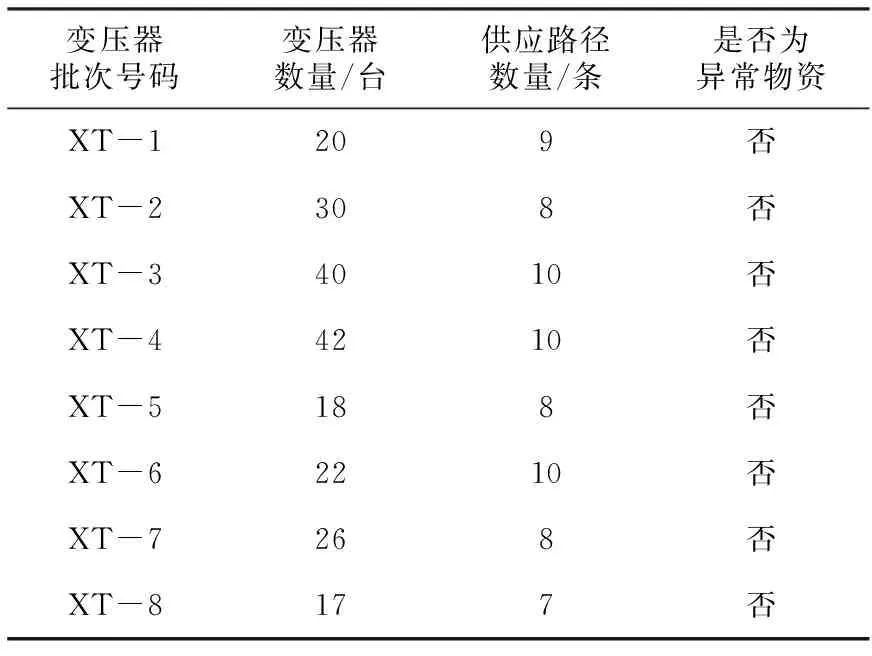
表2 变压器批次ID列表

2)根据历史数据总结得到供应过程中的实际数据与相关计算参数。历史数据中应包含整个物资供应过程中的实际数据和相关计算参数,其中部分数据见表1。

3)根据上述两部分数据,构建仿真环境。

将表中数据导入仿真软件中,构建实验数据库,并将其作为模型验证的数据来源。

3.3 仿真方案设计

本次仿真主要对模型的缺陷物资召回范围确定能力以及缺陷物资传播路径预测能力进行分析。

1)缺陷物资召回范围。

在确定缺陷物资召回范围时,追溯模型从正向追溯与反向追溯两方面进行分析。应用模型获取变压器批次以及相关的批次节点信息,通过正向追溯,可以确定与缺陷物资相关的起始批次。在确定起始批次后,对物资进行技术检测,确定缺陷物资中存在的异常环节,根据异常环节的检测结果,进行反向溯源,寻找缺陷批次的来源和确定召回范围。

2)缺陷物资传播路径预测。

对电力应急物资供应质量进行溯源分析,预测可能发生质量问题的路径,提升质量问题物资的召回率。路径追溯示意图如图3所示。

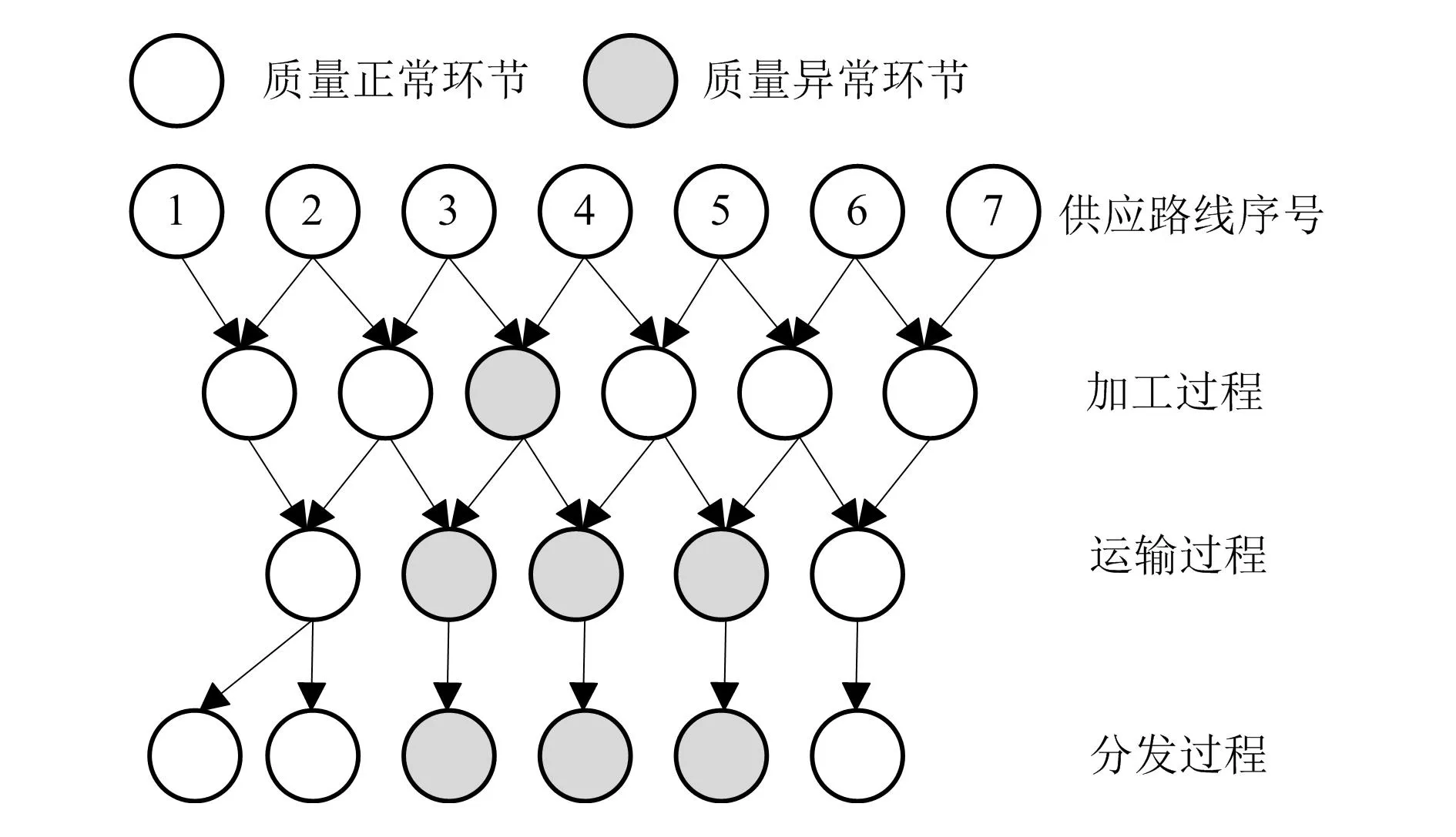
图3 路径追溯示意图

由图3可知,在对电力应急物资供应质量进行溯源分析,并预测可能发生质量问题的路径时,可以使用问题物资LK的召回率评估本文方法的使用效果,具体指标计算公式如下:

(15)

式中:V为异常物资召回率,LI为可追溯的物资量,LP为异常不可追溯物资量。

3.4 仿真结果分析

选取基于联盟区块链的追溯模型[10]与神经网络追溯模型[11]与本文模型进行对比分析,所得实验结果如图4所示。

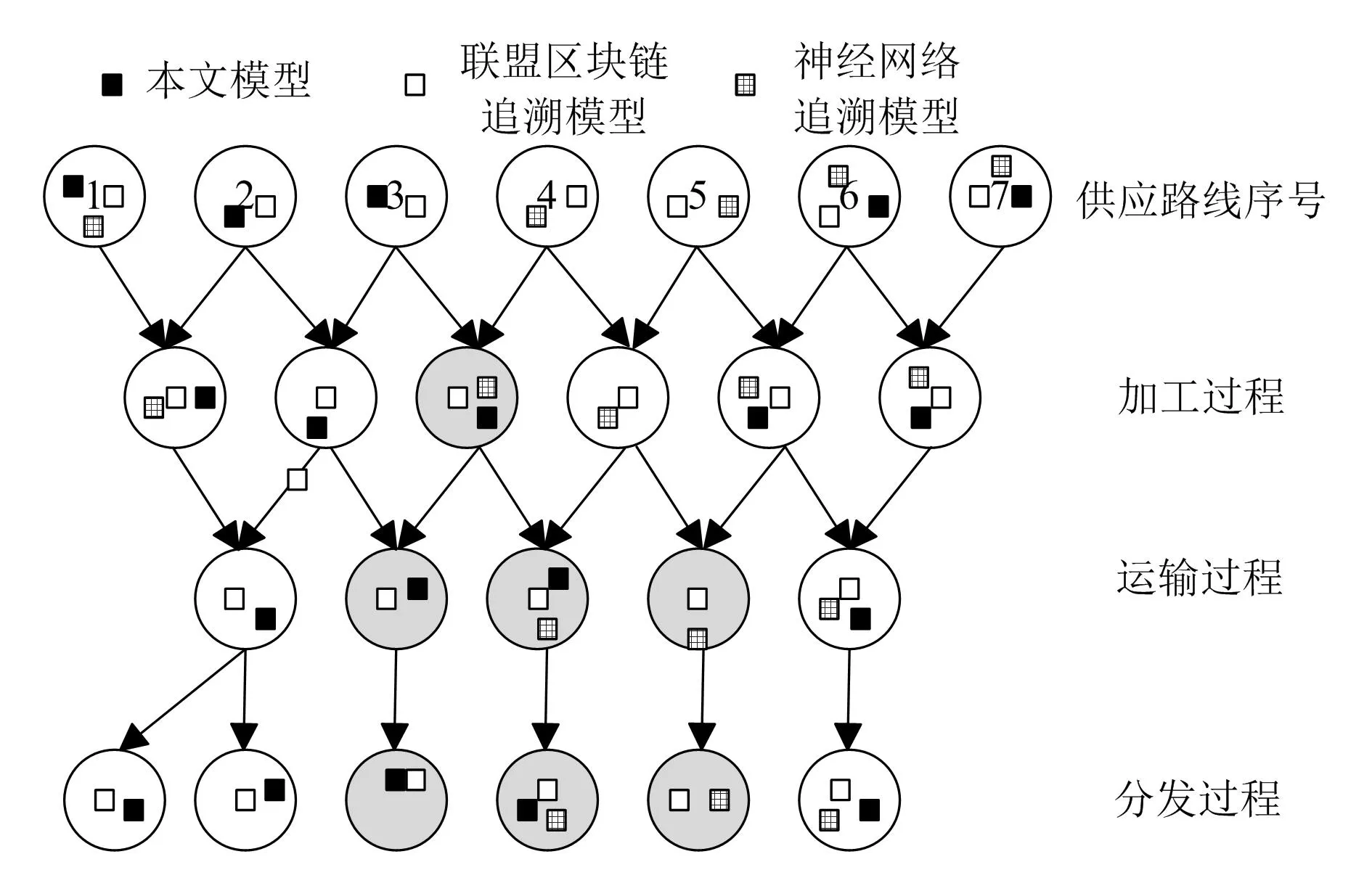
图4 路径追溯结果示意图

在应急物资召回过程中,联盟区块链追溯模型与神经网络追溯模型完成产品追溯效果较差,且造成大量的经济损失。而本文模型在一定程度上可以节约物资的追溯时间成本以及召回成本。由图4可知,本文模型可以在最短的路径内完成物资的追溯工作,将追溯结果整合为表格的形式,见表3。

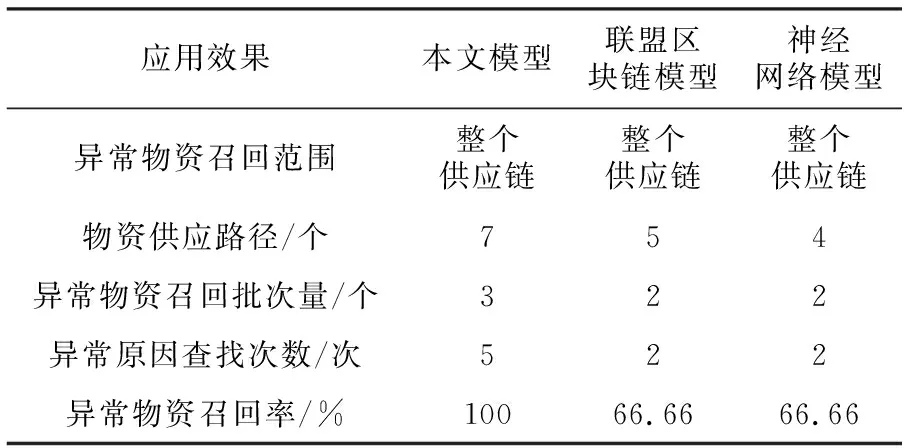
表3 追溯模型应用效果分析

由表3可知,应用不同模型进行分析后,在物资召回率以及异常物资的召回批次上存在着大量的差异,本文模型的异常物资召回范围相对较大且异常物资召回批次量较多,同时异常物资召回率相对较高。

4 结束语

电力应急管理过程中,应急物资质量对于电力系统的重建具有重要影响。本文构建了新型质量追溯模型,并通过仿真实验验证了模型的有效性。仿真实验结果表明,本文模型在物资追溯过程中能够在更短的时间内完成追溯工作,提高了召回效率,并且能够实现更高的异常物资召回率,为应急物资召回提供了一种更有效、更节约成本的解决方案。在日后的研究中应将人工智能技术结合到应急物资供应质量追溯过程中,以提升智能化管理水平,在保证供应质量的同时提升追溯模型的使用效果。