Joint Optimization of Resource Allocation and Trajectory Based on User Trajectory for UAV-Assisted Backscatter Communication System

Peizhong Xie ,Junjie Jiang ,Ting Li ,Yin Lu

1 School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2 Key Lab of Broadband Wireless Communication and Sensor Network Technology(Nanjing University of Posts and Telecommunications),Ministry of Education,Nanjing 210003,China

Abstract: The Backscatter communication has gained widespread attention from academia and industry in recent years.In this paper,A method of resource allocation and trajectory optimization is proposed for UAV-assisted backscatter communication based on user trajectory.This paper will establish an optimization problem of jointly optimizing the UAV trajectories,UAV transmission power and BD scheduling based on the large-scale channel state signals estimated in advance of the known user trajectories,taking into account the constraints of BD data and working energy consumption,to maximize the energy efficiency of the system.The problem is a non-convex optimization problem in fractional form,and there is nonlinear coupling between optimization variables.An iterative algorithm is proposed based on Dinkelbach algorithm,block coordinate descent method and continuous convex optimization technology.First,the objective function is converted into a non-fractional programming problem based on Dinkelbach method,and then the block coordinate descent method is used to decompose the original complex problem into three independent sub-problems.Finally,the successive convex approximation method is used to solve the trajectory optimization sub-problem.The simulation results show that the proposed scheme and algorithm have obvious energy efficiency gains compared with the comparison scheme.

Keywords: energy efficiency;joint optimization;UAV-assisted backscatter communication;user trajectory

I.INTRODUCTION

With the appearance and development of the Internet of Things and its large-scale commercial use,the energy problem of node batteries has become a major factor restricting its development,and the backscatter communication technology came into being[1-3].The backscatter device does not need to use any complex and high-power active RF wave components.It can not only reflect the incident RF wave by adjusting the impedance of the device to achieve information transmission,but also collect energy from the incident RF wave[4,5].This will reduce the power consumption of the node circuit and extend its service time,thus providing an energy-saving solution for the communication of the Internet of Things devices[6].

Backscattering communication systems can be divided into the following categories: single-static backscattering communication systems,double-static backscattering communication systems and environmental backscattering communication systems [7].The single static backscatter communication system is that the carrier wave transmitter and signal receiver are set on the same equipment,the received backscatter signal has experienced two signal fading,and is also affected by the double near-far problem.The carrier transmitter and signal receiver of the dual-static backscatter communication system are separate.Selecting the appropriate location of the carrier transmitter can greatly improve the performance of the dual-static backscatter communication system.However,the double-static backscatter carrier transmitter is bulky and expensive to deploy,and will cover huge economic costs in the actual production environment.The carrier transmitter used in the environmental backscatter communication system is the environmental RF source with other functions and utilization value,including a TV tower,cellular base station,Wi-Fi signal,etc.Since the modulated environmental RF signal is a unpredictable dynamic signal,it will directly interfere with the signal receiver,which greatly limits the performance of the environmental backscatter communication system[8-10].

Unmanned aerial vehicle (UAV) assisted wireless communication has gained widespread attention from academia and industry in recent years benefiting from its wide coverage,high mobility,low cost and high probability of line-of-sight links[11-13],Lei Lang et al.[14]maximized the minimum average rate of users by optimizing the flight path and bandwidth allocation of UAVs in the downlink wireless transmission system of UAV-assisted mobile user communication.In[15],the author put forward a UAV broadcast coverage strategy that can maximize energy efficiency.

Considering the disadvantages of the above backscatter communication system,the UAV is introduced into the backscatter communication network.In [16],the author studied UAV assisted environment backscatter system,analyzed the outage probability of downlink backscatter communication and derived the asymptotic outage probabilities of infinite RF signal power and infinite Nakagami fading parameter.In [17],the author studied UAV assisted NOMA backscatter communication system,optimized the scheduling of energy collection time,the gateway amplification factor,and the location of the UAV to maximize the sum rate of system.In[18],the author proposed a backscatter communication network with a UAV equipping a carrier wave transmitter and a signal receiver at the same time.The UAV collects the BDs data and transmits it back to the base station.The throughput of the backscatter communication system is maximized by optimizing the trajectory,time distribution and backscatter coefficient of the UAV.Authors in [19] and [20] considered that UAVs are equipped with a carrier wave transmitter and a signal receiver at the same time,and a non-orthogonal multiple access communication scheme is selected to transmit information.In [19],authors maximized the number of bits successfully decoded in the uplink and minimized the flight time by optimizing the flight altitude of UAVs.In [20],authors optimized the hover position,reflection coefficient,and transmission power of UAV to maximize the total rate of nodes.Fan et al.[21]considered that multiple UAVs are used for time division multiple access communication,and the average node rate is maximized by optimizing UAV trajectory,reflection coefficient,and transmission power.

The UAV-assisted backscatter communication network has shown better performance improvement in communication quality,but UAV battery energy consumption cannot be ignored.Therefore,issues related to energy consumption have been studied.In [22],authors considered that the scenario of UAV-assisted backscatter and HTT hybrid network model.UAV provides energy for the hybrid network.By optimizing the transmission power and trajectory of the unmanned aerial vehicle,the backscatter reflection coefficient of the Internet of Things nodes and the transmission power of active transmission,the total energy efficiency of all Internet of Things nodes is improved.However,the energy consumption considered in this paper is the BDs and active transmission,The flight energy consumption of UAV is ignored which is the largest power consumption.In [23],authors considered that The UAV flew from the base station to the hover position to collect data,and then flew back to the base station to transmit data.The energy efficiency was maximized by determining the optimal hover position.its energy consumption is UAV flight energy consumption and hover energy consumption.Since UAV flight power and hover power are fixed values during constant speed flight and hover,it is sufficient to study flight time and hover time.In [24],authors used the energy consumption model of UAV dynamic flight speed to calculate energy consumption accurately,which considers the impact of trajectory and speed on flight energy consumption.This paper studies the backscatter communication system that UAV is with a signal receiver and the position of the carrier transmitter is fixed,authors improved the system energy efficiency by optimizing the trajectory of UAV,node scheduling and transmission power of the carrier transmitter.

At present,the research on UAV-assisted backscatter communication systems is based on the fixed position of BDs,while BDs may be mobile in reality.For mobile BDs,it is difficult to obtain instantaneous channel state information dynamically,but when the BD dynamic path is predictable,large-scale channel state information can be obtained in advance,and it can solve the problem effectively.

In this paper,considering the backscatter communication system model of UAV equipped with a carrier wave transmitter and a signal receiver,and the moving path of ground backscatter equipment can be predicted,the trajectory and resource allocation of UAV are researched to improve the energy efficiency of the system.Firstly,the UAV transmits radio frequency carrier wave to the moving ground backscatter equipment,and then the BDs use part of the received sine signal for power supply and part of the sine signal for modulation to send to the UAV,and finally the UAV receives the signal to complete data acquisition.Setting the minimum energy consumption requirements of the ground reflecting equipment and the minimum data collection limit,the energy efficiency of the system is maximized by jointly optimizing the trajectory of the UAV,the launch power of the UAV and the mobile BD scheduling.When designing the optimization problem solving algorithm,the original fractional optimization problem is first converted into an equivalent integer problem based on Dinkelbach algorithm,and then the block coordinate descent method is used to decompose into sub-problems,and finally the successive convex approximation algorithm is used to solve the sub-problems.

The main contributions are as follows:

1) Since the backscatter equipment is mobile,a UAV-assisted backscatter communication system model consisting of a UAV that equips a carrier wave transmitter and a receiver and multiple mobile BDs is adopted.An optimization objective function is constructed to maximize the total energy efficiency of the system and meet the minimum energy collection constraints,minimum transmission data volume constraints,and maximum transmission power constraints.The problem is a non-convex,nonlinear,multivariable coupled optimization problem,and it is difficult to obtain the analytical solution directly.

2) This paper will propose the DBS algorithm(Dinkelbach-Block Coordinate Descent-Successive Convex Approximations)to solve the problem.Firstly,the objective function is converted into a nonfractional programming problem based on Dinkelbach method,and then the original problem is converted into three sub-optimization problems to solve the multivariable coupling problem using the Block Coordinate Descent method;Finally,the non-convex optimization problem is converted into a convex optimization problem by using the Successive Convex Approximations algorithm.This paper will introduce the specific algorithm steps.

3)This paper will build the simulation environment to verify the feasibility of the scheme.The simulation results show that the proposed scheme has obvious energy efficiency gain compared with the comparison scheme,and the proposed algorithm can effectively solve the problem and has good convergence.

II.SYSTEM MODEL

As shown in Figure 1,This UAV-assisted backscatter communication system includes K mobile BDs and a UAV with a carrier wave transmitter and a signal receiver,and K BDs are represented byKall ∈{1,2,...,N.}

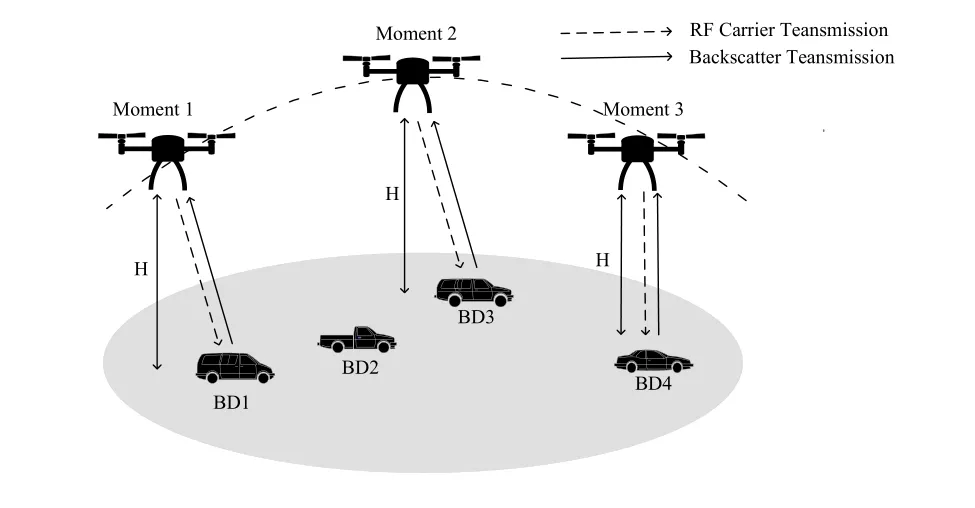
Figure 1.The UAV-assisted backscatter communication system.

To facilitate analysis,a two-dimensional coordinate system is introduced into the system model.Setting the task time toT.In timet ∈[0,T],because the dynamic trajectory of BD is known,the k-th BD coordinate is defined aswk(t)=[xk(t),yk(t)],wherexk(t)andyk(t)respectively represent the abscissa and ordinate of the k-th BD at time t.The plane coordinates of the UAV are defined asq(t)∈[x(t),y(t)],wherexk(t) andyk(t) respectively represent the abscissa and ordinate of the UAV at timet,and the fixed flight height of the UAV is set asH.To simplify the analysis,the flight time is divided intoNtime slots that are small enough,and the duration of each time slot is represented byNall ∈{1,2,...,N}.The dynamic trajectory of BD can be approximately expressed as,n ∈{1,2,...,N}.The trajectory of the UAV can be approximately expressed as,n ∈{1,2,...,N},and the maximum speed of the UAV is expressed asVmax,so there are constraints on the position and speed of the UAV.

where ||·||represents the two-norm calculation symbol,δ=T/Nrepresents the length of each time slot,qIrepresents the initial position,andqFrepresents the final position.

Unlike the traditional terrestrial cellular network communication,the UAV can flexibly change its position,so the channel from the backscatter equipment BD to the UAV is dominated by the line-of-sight link.In the n-th time slot,the distance between the UAV and the k-th BD can be expressed as

In this paper,the time division multiple access(TDMA)dynamic transmission strategy is adopted to provide a communication scheme for the UAV auxiliary backscatter communication system,that is,the moving BD sends data to the UAV in turn,and the UAV flies according to the designed trajectory,and receives data from the BDs during the flight.Define a binary variableak[n]∈{0,1}to indicate whether the k-th BD sends data to the UAV in the n-th time slot.Ifak[n]=1,the k-th BD will send data;Otherwiseak[n]=0.At most one BD establishes communication with UAV at the same time,so there is the following constraint.

BDs can change the matching impedance of the antenna to modulate the data to the incident wave,and make the modulated signal to transmit to the UAV in the way of antenna reflection.The intensity of the reflected signal is related to the power reflection coefficient of BD and the transmitted power of the UAV.To simplify the model,whenak[n]=1,BD is in the state of total reflection,that is all energy can be used for reflected communication when the UAV establishes communication with the k-th node;Whenak[n]=0,BDs are in the state of energy collection.The carrier transmitter has power constraints.

wherePmaxrepresents maximum transmitting power of UAV.

In the process of energy collection,the backscatter device BD must have some energy loss due to internal circuit reasons.The wireless energy collection efficiency of the k-th BD is expressed byηk ∈(0,1).Therefore,the energy collected by the k-th BD in the whole mission cycle can be expressed as

where Ω0represents the path loss when the reference distance is one meter.

According to Shannon’s theory,the amount of data transmitted by the k-th BD in the whole task cycle can be expressed as

whereβ0represents the channel power gain when the reference distance is one meter,andσ2represents the additive Gaussian white noise at the UAV receiver.

In the UAV-assisted backscatter communication system,the total energy consumption of the system mainly includes carrier transmitter energy consumption and UAV flight energy consumption.The flight propulsion energy consumption of rotorcraft is determined by the flight speed and acceleration of UAV.In this paper,because the variable speed flight time of UAV only accounts for a small part of the total flight time of UAV,the additional energy consumption caused by UAV acceleration is ignored.The flight propulsion energy consumption power of UAV[14]is expressed as

Therefore,the energy efficiency of the UAV-assisted backscatter communication system can be expressed as

From the perspective of energy consumption,the optimization problem of maximizing the energy efficiency of UAV assisted backscatter communication system is established.The goal is to maximize the energy efficiency of the system through BD scheduling A,carrier transmission power P,UAV trajectory Q and UAV speed V,while ensuring the minimum communication throughput and working energy consumption of BD.The optimization problem(10)is as follows

III.PROPOSED ALGORITHM

3.1 Conversion of Equivalent Optimization Problems

The objective function of the original optimization problem has uncertain parameters and is difficult to deal with.Because Dinkelbach method is widely used to deal with nonlinear fractional optimization problems,this paper applies this method to deal with the energy efficiency objective function.With the aid of auxiliary variablesη*,the original objective function can be equivalently converted into

whereη*is the optimal energy efficiency.

For any given non-negative valueη ≥0,iff(η*)≤0,η ≥η*,it means that the current value needs to be reduced to make it tend to the optimal energy efficiency under the condition of ensuring(11).Similarly,iff(η*)≥0,η ≤η*,it means that under the condition of ensuring(11),it is necessary to increase the current value to make it tend to the optimal energy efficiency.Onlyη=η*then can we obtain the optimal energy efficiency.Therefore,the original optimization problem can be transformed into the following equivalent parameter optimization problem(12).

It is still a non-convex optimization problem because of the coupling relationship between optimization variables.For such problem,the block coordinate descent method is used to decompose it into three sub-optimization problems: scheduling optimization,power optimization,and trajectory optimization.

3.2 Scheduling Optimization

For the scheduling optimization subproblem,given the feasible carrier transmission power,flight path,speed,and auxiliary variables,the original problem is simplified to solve the scheduling of UAV and backscatter equipment.Since the uplink access variable of BD is a binary variable and needs to be processed continuously,the equivalent parameter problem of energy efficiency optimization(13)can be expressed as

Obviously,the optimization problem is a linear programming problem,which can be solved by existing optimization tools(such as CVX).

3.3 Power Optimization

For the power optimization subproblem,given the feasible scheduling variables,flight path,speed,and auxiliary variables,the original problem is simplified to solve the carrier transmission power of the optimal UAV,and the energy efficiency optimization equivalent parameter problem(14)can be expressed as

The objective function is a convex function,and the constraint conditionsC8 andC9 are convex functions,so the optimization problem is a convex optimization problem,which is solved by using convex optimization tools.

3.4 Trajectory Optimization

For the trajectory optimization subproblem,given feasible scheduling variables,launch power,and auxiliary variables,the original problem is simplified to solve the optimal UAV trajectory Q and the flight speed V varying with the trajectory.The equivalent parameter problem of energy efficiency maximization can be expressed as (15).The optimization problem has non-convexity and is difficult to solve because of nonconvex objective function and non-convex constraint termsC10,C11.The non-convex optimization problem needs to be converted into a convex optimization problem.It can be seen from formula(8)that the first term and the third term ofPUAV[n] are convex functions ofV[n],but the second term is non-convex.The non-convexity is solved by introducing relaxation variables{y[n]}.The process is as (16) while this formula can be equivalently transformed as(17).The optimization problem can be further obtained by substituting formula(18)into the optimization problem.

However,the optimization problem is still nonconvex because there are non-convex terms in the objective function,and the constraintsC10,C11 andC12 are non-convex.These four non-convex terms can be solved by continuous convex optimization technology.Specifically,the objective function and the constraint conditionC10 are convex functions ofH2+||wk[n]-q[n]||2.Because the first order Taylor expansion function of the convex function is the lower bound of the original function,the first order Taylor expansion obtains the lower bound of the original function.

The non-convex portion of the optimization problem is locally linearized using a first-order Taylor series expansion.The equation is considered valid when the expansion point within the local region corresponds to a local optimum.

For the non-convex constraint condition (18),the expression on the right side of the equal sign is a joint convex function of variablesy[n]andV[n].The lower bound of the expression on the right side of the constraint conditionC12 can be obtained by using the continuous convex optimization technique.

where{y{l}[n]}is obtained after thel-1 iteration,and{y{l}[n]}is a constant.The lower bound of inequality(20)is a linear function of variablesy[n]andV[n].The equation is satisfied wheny{l}[n]andV {l}[n]are local optimums.For constraint conditionC6,its lower bound function is obtained by Taylor first-order expansion

Replace the logarithmic function of the objective function (18) and the constraint conditionC10 with the corresponding lower bound according to formula (19);Replace the right part of the constraint conditionC12 with its lower bound according to formula(20);According to formula(21),replace the left function of constraint conditionC11 with its lower bound,and then problem(18)is optimized to(22)by continuous convex optimization technology.

The global optimal solution of problem (22) is the lower bound of the global optimal solution of problem(15).First,the feasible region of problem (22) is a subset of the feasible region of problem(15),because once the constraintsC14,C15 andC16 are satisfied,the constraintsC10,C11 andC12 must be satisfied.Secondly,because problem (22) uses the continuous convex optimization technique to take the lower bound of the objective function of problem(15),the optimal energy efficiency value of problem (22) must not exceed the value of problem(15).

The proposed DBS algorithm is summarized and listed in Algorithm 1.The number of iterations for the DBS algorithm is defined asKite,according to literature [25],when the convergence threshold isϵ,The computational complexity of the Dinkelbach algorithm isO（1/ϵ2log（3K2N3））.Set the convergence threshold of the interior point method toζ,the complexity of each complex iteration of steps 2,3,and 4 isO(log(1/ζ)).In summary,the computational complexity of DBS isO（Kite·1/ϵ2log（3K2N3）·3log(1/ζ)）.

IV.SIMULATION RESULTS

The UAV-assisted backscatter communication systems work at the frequency of 900MHz.It is assumed that there are four users moving along the known track in the square area,as shown in Figure 2.The starting coordinates of user 1,user 2,user 3,and user 4 are(50,50),(50,450),(450,450),(450,50),and (450,50)respectively moving in a uniform straight line towards(50,450),(450,450) and (450,50),and starting at the same time.The maximum power of the carrier transmitter is set asPmax=6W.Each node must meet the lower energy limit with=1*1014J.The flight altitude of the UAV is set asH=50m,its maximum flight speed is set asVmax=20m/s.The other parameters as follow:β0=0.1,η=0.5,σ2=-144dBm.This paper divides the flight time into 100 time slots.The parameters of rotorcraft are set according to the parameters in reference [24].Table 1 lists the values of various parameters involved in the flight dynamics model of rotorcraft.

Table 1.Parameters of UAV.

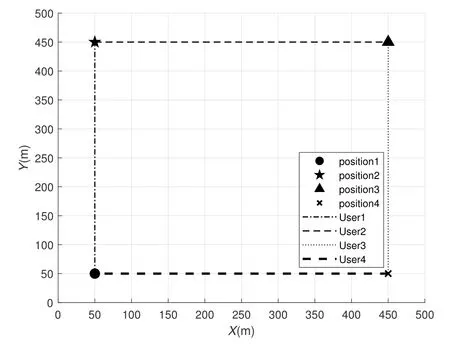
Figure 2.The user trajectory.

The simulation first considers the trajectory optimization of UAV,where Figure 3 and Figure 4 show the flight path optimization results of UAV under Case 1 and Case 2,taking into account two situations of UAV at different starting points and ends and at different mission times.

Figure 3.UAV optimal trajectory in Case 1.

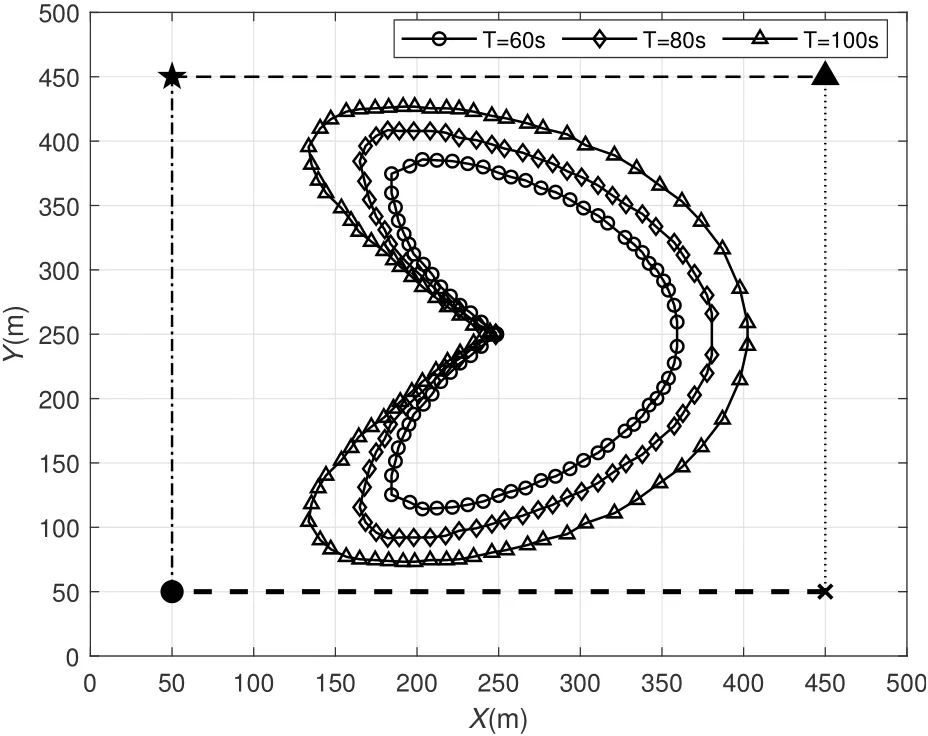
Figure 4.UAV optimal trajectory in Case 2.

Case 1.The starting point and ending point of the UAV are set as(50,50).

Case 2.The starting point and ending point of the UAV are set to(250,250). At the same time,adjust the known trajectory of user 1 to a uniform linear motion from(50,450)to(50,50).

It can be seen from Figure 3 and Figure 4 that although the starting and ending positions of the UAV are different,and the user trajectory is slightly adjusted,the optimal trajectory of the UAV in both cases is as close as possible to the user trajectory,and the distance between the UAV and the user is shortened,which indicates that the optimized trajectory is closer to the user,and better large-scale channel status is obtained,and larger data transmission volume is obtained.In addition,when the task time is changed,the optimal flight path is also different.With the increase of the task time,the complexity of the optimal trajectory of the UAV also increases,and the optimal trajectory is also closer to the user’s trajectory.This shows that the longer the mission time,the larger the flight path optimization space,and the better the trajectory optimization effect.

Figure 5 shows the time resources allocated by the UAV to four users in Case 1.Figure 6 shows the reflected power distribution of four users when the task time is set to 80 s.At the same time,it can be seen from the optimal trajectory of the UAV in Figure 3 that the user’s scheduling depends on the distance between the UAV and the user,and the UAV will establish communication transmission with the user closest to the current time.Observe Figure 3 and Figure 5.With the increase of task time,the trajectories close to User 1 and User 4 become longer and the scheduling time also becomes longer,indicating that under the condition of meeting the data volume constraints of User 2 and User 3,increasing the scheduling time of User 1 and User 4 can achieve better energy efficiency.

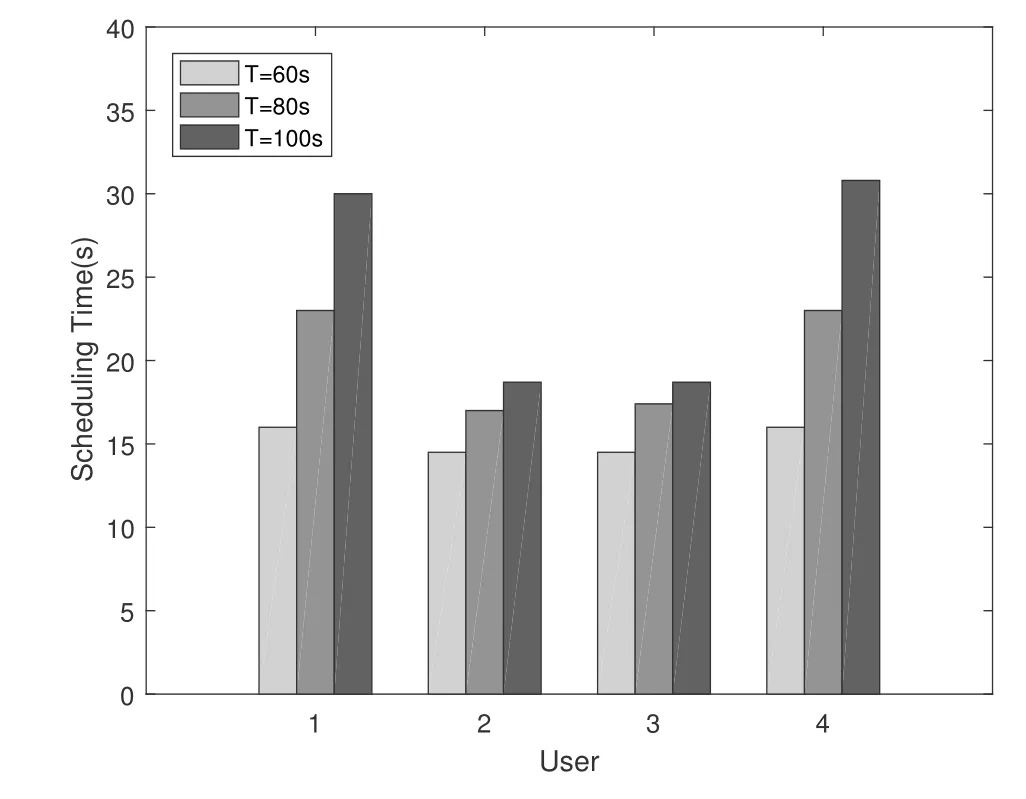
Figure 5.Time resource allocation in Case 1.

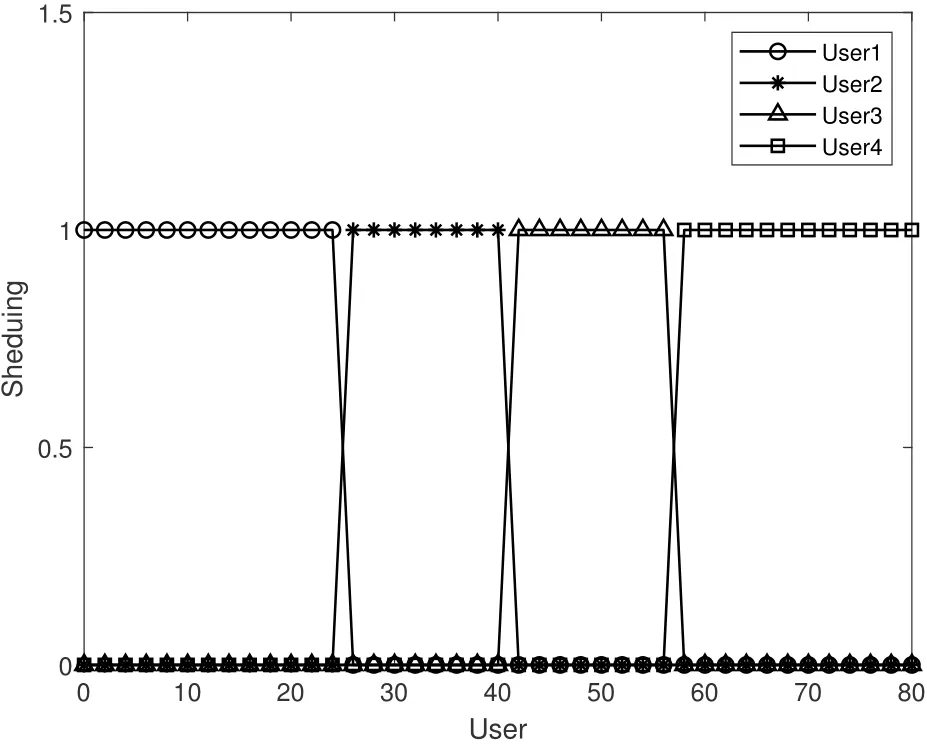
Figure 6.User scheduling distribution in Case 1.

Figure 7 shows the time resources allocated by the UAV to four users in Case 2.Figure 8 shows the reflected power distribution of four users when the task time is set to 80 s.Observe Figure 4 and Figure 8.With the increase of task time,the trajectories close to user 2,user 3 and user 4 become longer and the scheduling time also becomes longer,indicating that under the condition of meeting the data volume constraint of user 1,increasing the scheduling time of other users can achieve better energy efficiency.

Figure 7.Time resource allocation in Case 2.

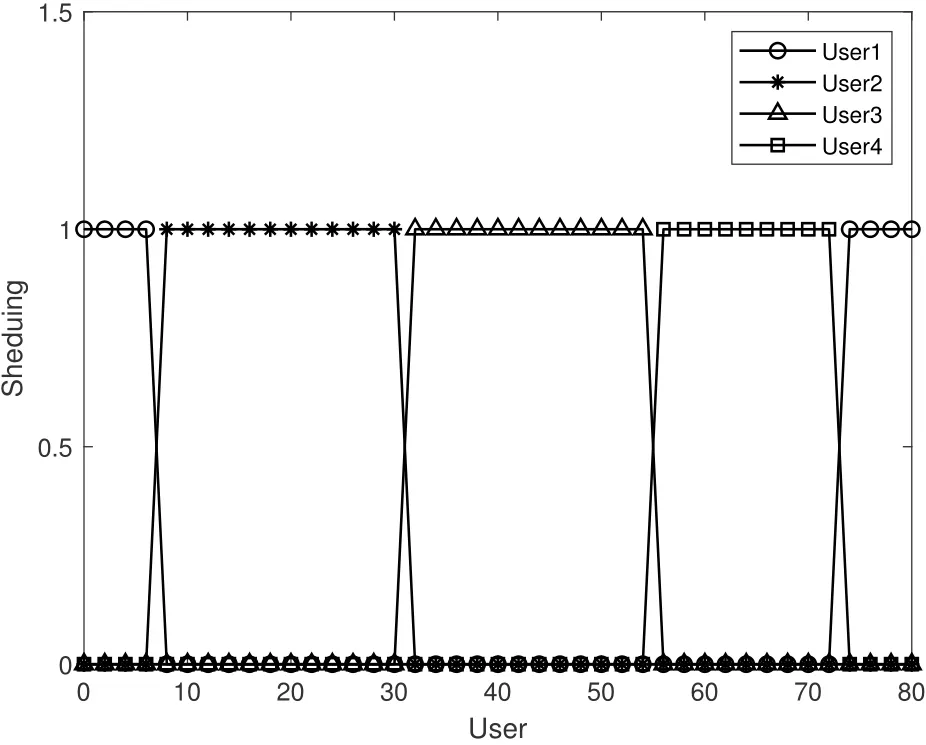
Figure 8.User scheduling distribution in Case 2.

To verify the convergence of the algorithm,Figure 9 shows the relationship between different task times and convergence.It can be observed that when the task time is 60s,the energy efficiency will converge after 6 iterations;When the task duration is 80 s,it will converge after 10 iterations;When the task time is 100s,it will converge after 12 iterations.The experimental results show that the convergence decreases slightly with the increase of task duration.At the same time,it was found that under the initial trajectory setting,the longer the task time,the lower the energy efficiency.This is due to the relatively unreasonable initial trajectory,the longer the mission time increases the flight energy consumption,but does not improve the quality of data transmission;however,when the algorithm converges,the longer the task time is,the higher the energy efficiency is.This is because the optimal trajectory improves the communication transmission quality on the one hand,and optimizes the UAV energy consumption on the other hand.

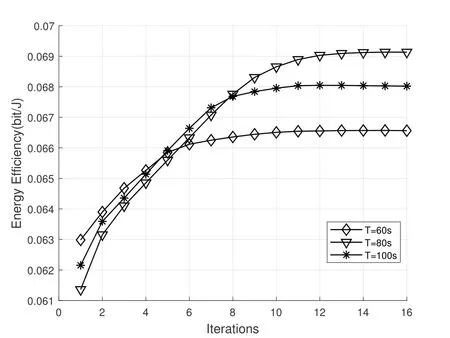
Figure 9.Effect of different task times on convergence.

Finally,the performance of the methods used in this paper is evaluated and two sets of comparison schemes are proposed.Scheme 1 is based on the design presented in[24],which is different from the setup in reference[24]that employs multiple carrier transmitters.Considering the cost implications in practical applications,this paper only utilizes a single carrier transmitter,aligning with the assumptions made in this study.A high-power carrier transmitter is set at(250,250)to achieve optimal energy efficiency by optimizing BD scheduling,UAV transmission power and UAV trajectory.Scheme 2 represents a scenario without trajectory optimization for the unmanned aerial vehicle(UAV),assuming stationary hovering of the UAV.This approach is consistent with the common practice observed in UAV-assisted communication systems.It can be seen from Figure 10 that the energy efficiency of the proposed scheme in this paper is the best.The energy efficiency of the second scheme decreases with the increase of time.This is because the hovering flight of the UAV is a state of high energy consumption,and the growth rate of energy consumption over time exceeds the rate of data volume.

Figure 10.Comparison of energy efficiency of different schemes.

V.CONCLUSION

This paper researches UAV-assisted backscatter communication systems,which is composed of multiple mobile BDs and a UAV with carrier transmitter and receiver.Firstly,by jointly optimizing BD scheduling,UAV launch power and UAV trajectory,the system model of energy efficiency optimization is established under the constraints of BD throughput and working energy consumption,and then a DBS algorithm based on Dinkelbach algorithm,block coordinate descent algorithm and continuous convex optimization technology is proposed.Because the original problem is a nonlinear fractional optimization problem,Dinkelbach algorithm transforms the original problem into an equivalent integral optimization problem;The block coordinate descent method decomposes the equivalent integer optimization problem into three subproblems and solves three coupling problems of solving variables;The successive convex approximation technology completes the approximate solution of nonconvex subproblems of trajectory optimization.Finally,the system is simulated,and the results show that the energy efficiency of the proposed scheme is significantly higher than that of the original scheme,and the proposed algorithm has better convergence.Under the research background of this paper,the choice of communication scheme using NOMA is also a problem worth studying.