Mutual Information Maximization via Joint Power Allocation in Integrated Sensing and Communications System

Jia Zhu,Junsheng Mu,Yuanhao Cui,Xiaojun Jing

School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China

Abstract: In this paper,we focus on the power allocation of Integrated Sensing and Communication(ISAC)with orthogonal frequency division multiplexing (OFDM) waveform.In order to improve the spectrum utilization efficiency in ISAC,we propose a design scheme based on spectrum sharing,that is,to maximize the mutual information (MI) of radar sensing while ensuring certain communication rate and transmission power constraints.In the proposed scheme,three cases are considered for the scattering off the target due to the communication signals,as negligible signal,beneficial signal,and interference signal to radar sensing,respectively,thus requiring three power allocation schemes.However,the corresponding power allocation schemes are nonconvex and their closed-form solutions are unavailable as a consequence.Motivated by this,alternating optimization(AO),sequence convex programming(SCP) and Lagrange multiplier are individually combined for three suboptimal solutions corresponding with three power allocation schemes.By combining the three algorithms,we transform the non-convex problem which is difficult to deal with into a convex problem which is easy to solve and obtain the suboptimal solution of the corresponding optimization problem.Numerical results show that,compared with the allocation results of the existing algorithms,the proposed joint design algorithm significantly improves the radar performance.

Keywords: coexistence;communications;multicarrier radar;mutual information;spectrum sharing

I.INTRODUCTION

1.1 Background and Motivation

As an emerging technology,ISAC has attracted the significant attention of many researchers in recent years[1-3].This provides an exciting opportunity to use wireless infrastructure to achieve sensing,so that future communication networks will not only be able to provide communication services,but also provide ubiquitous sensing services to sense the surrounding environment [4-7].This technology will be used in the Internet of things (IoT),vehicular-to-everything(V2X) communications,beyond 5G (B5G) and 6G[8,9].

However,due to the different demand for radar and communication function,realizing such a integrated is non-trivial.If the spectrum coexistence of radar and communication system can not be solved perfectly,not only the system gain can not be realized,but also the performance of radar and communication system will be degraded.Some excellent work has been done to solve the spectrum coexistence and performance problems in ISAC.Multicarrier waveforms are considered as one of the best candidates for spectrum coexistence of radar and communication systems [10].[11] introduces interference cancellation technology into the study of spectrum coexistence in ISAC system.[12] proposes to apply mutual information as a performance metric to radar waveform design.[13]proposes a resource allocation scheme for ISAC,with a focus on security and robustness.

A radar waveform design scheme based on radar mutual information criterion is proposed in[14]to improve the performance of radar system.[14]fully considers the influence of communication scattering on radar system,and studies the power allocation algorithm according to different criteria.[15]further studies this issue and gives a closed-form solution of radar subcarrier power allocation when minimizing system power.However,[14] and [15] only study the problem of radar power allocation when the cummunication signal has been determined.[16] considers the issue of joint power allocation in ISAC system and proposes a joint optimization scheme.The influence of scattering off the target due to the communication signals on radar performance is ignored in[16].However,in some practical applications,the scattering off the target due to the communication signals has an impact on radar sensing.For example,in a V2X scenario shown in Figure 1,the base station(BS)not only communicates with the vehicle,but the radar sensing of the vehicle itself is also affected by the communication signal emitted by the BS and the scattering caused by the communication signal.

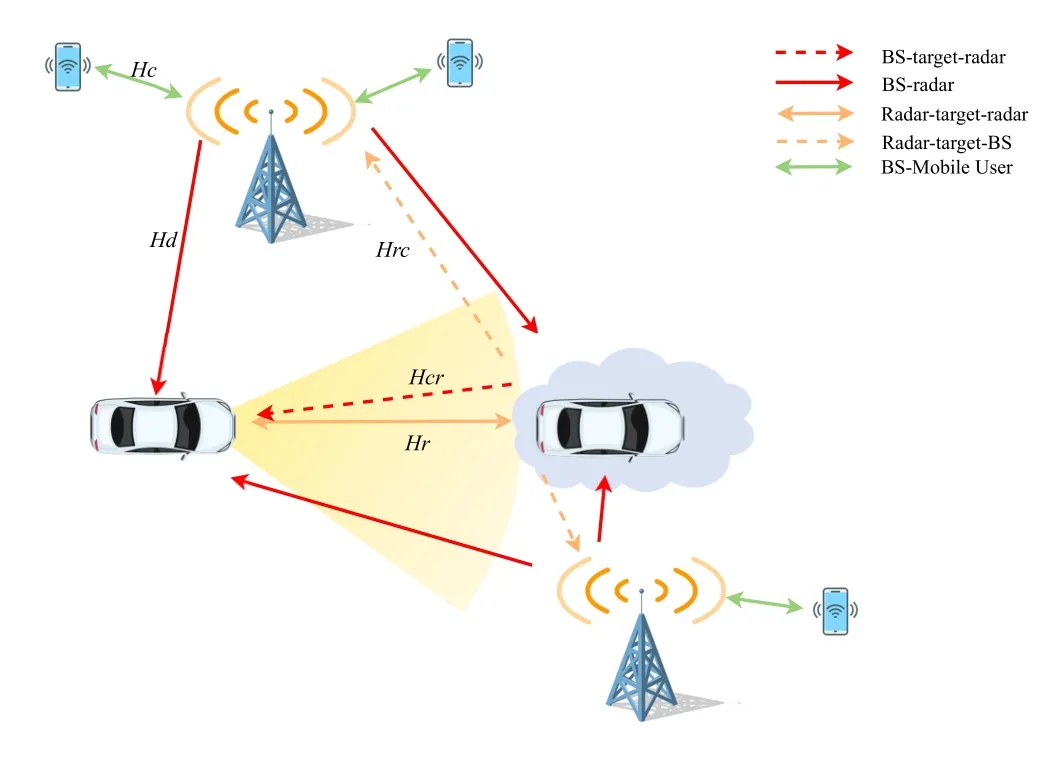
Figure 1.Scenario description of spectrum sharing in V2X.

The ISAC technology applied to V2X can detect the front target in real time and take into account the communication of the roadside unit [17].This paper focuses on the joint power allocation of radar and communication systems,and investigates the influence of scattering off the target due to the communication signals on radar sensing.However,the previous research focused on power allocation not only optimizes the power of radar system or only the power of communication system,but ignores the joint power allocation of radar and communication system.

1.2 Major Contribution

Inspired by the MI based criteria in[14]and[15],we consider the different processing methods of the communication scattered signals on the target.With different design criteria,the corresponding joint power optimization problems are formulated and solved analytically.

1.Different from the power allocation schemes in references [14] and [15],we use the joint design method to allocate power.Specifically,instead of only optimizing the radar transmit power or communication transmit power on each subcarrier,we propose a joint optimization algorithm to optimize the radar and communication transmit power allocated to each subcarrier at the same time.By maximizing radar MI and satisfying certain communication rate and transmit power constraints,the optimal power allocation strategy for radar and communication system is obtained.

2.Joint design makes optimization problems tricky because the optimization formula contains two optimization variables that are coupled to each other.To solve this challenge,we reformulate the optimization problem as a univariate optimization problem concerning radar and communication power through alternate optimization technique.Then Lagrange multiplier and sequence convex programming(SCP)are used to solve the reformulated subproblems.First of all,we assume that the communication power is fixed and optimize the radar system power.After the optimal radar system power allocation is obtained,the radar power is fixed and the communication system power is optimized.The radar power optimization problem is a convex optimization problem,and the closed-form solution of optimal power allocation can be obtained by Lagrange multiplier method.The communication power optimization subproblem is a non-convex optimization problem,and we employ the SCP method to transform it into an approximate convex optimization problem of the original problem for solution.

3.The numerical simulation results show that the performance of the joint design is much better than that of the unilateral design.In addition,the results also tell us that considering the communication signal as a useful signal can improve the performance of the radar system.

1.3 Organization

The remainder of this paper is structured as follows.Section II presents the scenario for our optimization problem and outlines the corresponding system model.In Section III,we propose solutions for obtaining suboptimal power allocation strategies.The effectiveness of our algorithm is verified through numerical simulation experiments,with results supporting our theoretical analysis presented in Section IV.Finally,Section V offers concluding remarks on the research presented in this paper.

II.SYSTEM MODEL

We simplify the paradigm of the research scenario as shown in Figure 2,where the system consists of a BS and a monostatic radar.Taking the V2X scenario as an example,the radar transmits signals to detect the vehicles ahead,the BS is responsible for the communication function of the mobile users within the cell,and the target vehicle is also one of the users covered by the BS.The signal received by the radar receiver mainly comes from two paths,one path is the radar echo directly from the target,and the other path is the scattering of the base station communication signal on the target.There are five types of signal links in Figure 2,representing the following:hcis the BS-Mobile user link inside a BS cell,hdis the direct BS-radar link,hris the radar echo link,hcris the BS-targetradar link andhrcis the Radar-target-BS link.

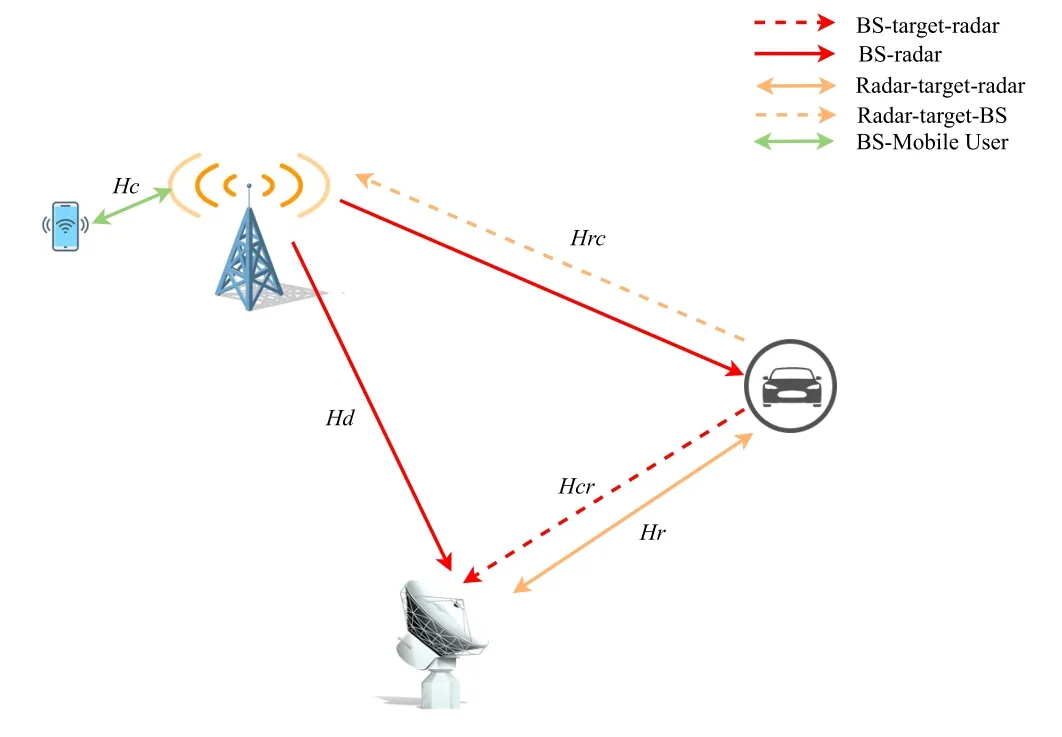
Figure 2.System model considered in our paper.

Before proceeding with further analysis,we propose some assumptions to simplify the process while preserving the rigor of the paper.

• The radar antenna beam is directional and only points to the target to be detected rather than directly toward the base station,that is to say,the base station will not receive the radar signal from the direct path,but receive the radar scattering signal.

• In order to focus on the core problem without deviation,we assume that the influence of time delay and Doppler shift in this system has been perfectly compensated[18].

• The radar and communication systems are assumed to have the same symbol rate and be synchronized in terms of sampling time and initial phase[19].

Many excellent characteristics of OFDM waveform make it a candidate waveform for ISAC[20,21],so we assume that both radar and communication systems use OFDM waveform in the same frequency band of bandwidthBHz.Suppose the OFDM waveform hasNsubcarriers,and frequency spacing of adjacent subcarriers is Δf=B/N.

For the radar system,we assume Pr=[Pr,1,Pr,2,...,Pr,N]Tdenote the radar powers which are to be determined.The radar transmission signal can be formulated as

wheredr(t) is unit-energy radar waveform,fcis the carrier frequency.

For the communication system,the communication transmission signal can be formulated as

wheredc(t)is unit-energy communication waveform,Pc=[Pc,1,Pc,2,...,Pc,N]Tare communication powers allocate to theNsubcarriers.fcis the same carrier frequency as the radar system.

At the radar receiver,we formulize the received signal as follows

wherer(t)is s the echo signal through the direct path,cc(t)is the communication signal directly received by radar receiver,cd(t) is the communication signal radiated from the BS via target scattering.nr(t) is the additive colored noise with known variance.hris the propagation path of radar echo,hdis BS-radar path,hcris the BS-target-radar path[15].

At the communication receiver,we formulize the received signal as follows

wherec(t) is s the received communication signal through the direct path,rc(t) is the radar signal radiated from the radar system via target scattering.nc(t)is the additive colored noise with known variance.hcis the propagation path inside BS cell,hrcis the Radartarget-BS path.

Before formally stating the optimization problem,we represent the signals received by radar and communication systems in vector notation,respectively.

where S,X are Discrete Fourier Transform(DFT)matrix ofs(t),x(t).hr,hd,hcr,hcand hrcdenote corresponding channel frequency response vectors,respectively.nrand ncrepresent the zero mean Gaussian random noise vectors with known covariance matrices,respectively.

And if you go to Madrid, and walk through the streets till you come to the highest church, you will see Medio Pollito perched on his one leg on the steeple, with his one wing drooping23 at his side, and gazing sadly out of his one eye over the town

III.PROPOSED APPROACHES

In this part,we propose three power allocation criteria according to the different ways of utilization of communication signals scattered by the target.The first one is to ignore the communication scattered signal,and under the constraints of communication user rate and system power,we jointly optimize the allocation of radar power and communication power to maximize the radar MI.The second one is to treat the communication scattered signal as a beneficial signal,and we maximize radar MI through joint power allocation optimization.The third one is to treat the communication scattered signal as an interference signal,and then obtain the optimal power allocation result of the radar and communication system under the constraints of communication rate and system power.

To facilitate discussions,we defined the channel coefficientgr,n=|hr[n]|2,gc,n=|hc[n]|2,grc,n=|hrc[n]|2,gcr,n=|hcr[n]|2,gd,n=|hd[n]|2.

3.1 Criteria A

For the communication system,communication rate is one of the most important metric to measure the performance of a communication system[22],which depends on the allocation of wireless resources such as power and communication bandwidth.The communication rate can be expressed by:

For the radar system,we consider the communication scattering signal received by the radar receiver is ignored.The figure of merit is the MI:

The joint power allocation problem maximizes the radar MI under communication rate and power constraints can be written as

where (9b) guarantees the quality of service of the communication system,the communication rate of thenth subcarrier should be higher than the threshold in the BS cell.(9c)is the total radiated power constraint for radar system,it ensures that the power of the radar system can’t be infinitely large,which is inconsistent with reality.(9d)denotes the total radiated power constraint for communication system and has the same physical meaning as constraint(9c).

The optimization problem(9)is non-convex,which is caused by two reasons,one is that the objective function(9a)is non-convex,it contains coupling variables,and the other is that the constraint (9b) is also non-convex,and it also contains coupling variables.Although the non-convex optimization problem is intractable,we decompose it into two optimization subproblems by an AO procedure,and then obtain a suboptimal solution to the original problem by Lagrange multipliers and SCP.The core idea of AO algorithm is to iteratively solvePrwhile keepingPcconstant,and vice versa,until the convergence threshold we set is reached[23].

Specifically,by fixingPc,we have the following subproblem:

where objective function (11a) is concave,(11b) and(11c) are both linear constraints.Therefore,(11) is a convex optimization problem and then we can use Lagrange multiplier method to solve it [24].Then,under a minimum communication rate constraint and a maximize total radiated power constraint,the optimal OFDM radar and communication power allocation corresponding to (11) that maximizes the radar MI should satisfy equation(12),

whereλ3is a variable determined by the constraint on the transmitted radar power.

After the optimal radar power allocation is obtained,the variablePrcan be fixed to the constant,and then we can solve the subproblem (13) to obtain the optimal communication power allocation.

The objective function (13a) in (13) is a difference of two concave functions is shown below:

where

We use SCP technology to solve(13).With the help of Taylor expansion method,(14)is approximately expressed in a linear form as:

This is a convex problem and many methods can solve it efficiently such as CVX [25].By setting the convergence condition |-|≤µ,the optimal radar power allocation scheme can be obtained under the condition of meeting the system requirements.

3.2 Criteria B

Next,we consider the communication scattering signal received by the radar receiver as a signal beneficial to radar detection.The MI calculation formula of radar can be written as follows:

Similarly,The power optimal allocation problem of the joint radar and communication system can be formulated as follows:

Through analysis (22),we know that it has a similar mathematical structure to (9),so we use the same solution method to solve it.

Similarly,we first fixPc,then(22)is rewritten as:

Then,under a minimum communication rate constraint and a maximize total radiated power constraint,the optimal OFDM radar and communication power allocation corresponding to (24) that maximizes the radar MI should satisfy equation (25),whereλ3is a variable determined by the constraint on the transmitted radar power.

The objective function (26a) in (26) is a difference of two concave functions is shown below:

We take SCP technology to solve problem (26).With the help of Taylor expansion method,(29)is approximately expressed in a linear form as:

So,we have the lower bound of(26a),written as:

After the above operations,(26)can be re-expressed as follows:

This is a convex problem and many methods can solve it efficiently such as CVX.By setting the convergence conditionµ,the optimal radar power allocation scheme can be obtained under the condition of meeting the system requirements.

The iterative solution process of optimization problem (22) is similar to optimization problem (9),and the specific algorithm details are omitted here.

3.3 Criteria C

Another way to consider communication scatter signal received by radar receivers is to treat it as interference signals.This is because the communication scattered signal is usually a random signal,which is unknown to the radar receiver,and the processing increases the complexity of the system.In this case,the MI of the radar system is expressed as:

Proceeding as before,we formulate the optimization problem as follows:

Through analysis (35),we know that it has a similar mathematical structure to (9),so we use the same solution method to solve it.

Similarly,we first fixPc,then(35)is rewritten as:

Then,under a minimum communication rate constraint and a maximize total radiated power constraint,the optimal OFDM radar and communication power allocation corresponding to (36) that maximizes the radar MI should satisfy equation (37),whereλ3is a variable determined by the constraint on the transmitted radar power.

The objective function (38a) in (38) is a difference of two concave functions is shown below:

With the help of Taylor expansion method,(41) is approximately expressed in a linear form as:

So,we have the lower bound of(39),written as:

After the above operations,(38)can be re-expressed as follows:

This is a convex problem and many methods can solve it efficiently such as CVX.By setting the convergence conditionµ,the optimal radar power allocation scheme can be obtained under the condition of meeting the system requirements.

The iterative solution process of optimization problem (35) is similar to optimization problem (9),and the specific algorithm details are omitted here.

3.4 Computational Complexity Analysis

The computational complexity of the algorithm is determined by the number of loop iterations.As previously mentioned,we obtained a closed-form solution for the optimal power allocation under radar power constraints,significantly reducing the algorithm’s complexity.The optimal power allocation for the communication system is mainly determined by the number of iterations,m,and the number of joint iterations,denoted asL.The interior-point method was used to solve problem(20),(33),(45),and its computational complexity isO(N3.5).Thus,we can obtain the total computational complexityO(LmN3.5).

IV.SIMULATION RESULTS

In this section,we verify the correctness and superiority of the proposed algorithm through numerical simulation.From the analysis of the simulation results,the proposed waveform design algorithm can obviously improve the performance of the radar system.

4.1 Number Parameters

Throughout the simulations,three power allocation schemes are discussed.In our work,OFDM waveforms are selected as candidate waveforms for multicarrier radar and communication systems.We set the number of subcarriersN=128,which not only takes into account the actual situation of multicarrier but also takes into account the amount of simulation calculation.The variances of the zero-mean white Gaussian noise for both systems are set asσc=1.2×10-13W andσr=1.6×10-13W,respectively.The detailed experimental parameters are shown in Table 1.

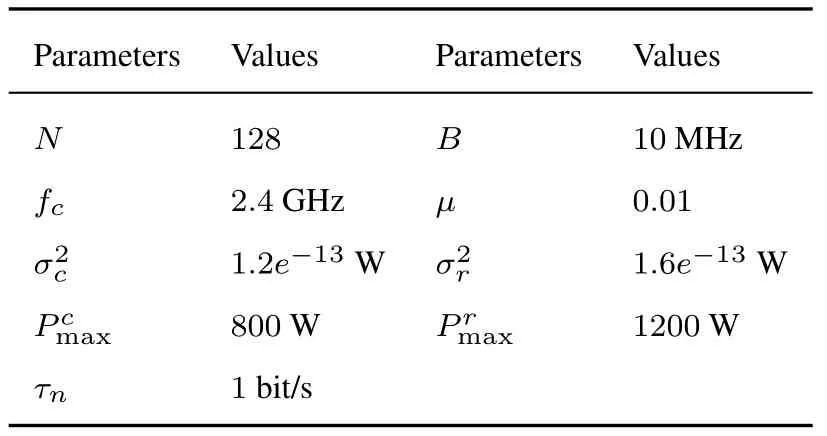
Table 1.Simulation parameters.

As a comparison,we consider the MI of the radar system when the unilateral design strategy is adopted and the MI of the radar system when the power joint design is adopted.The so-called unilateral design here means that only the power allocation of the radar subcarriers is optimized,while the power on the communication subcarriers is known and determined.This situation is considered in [14] and [15].It should be noted that,the communication rate mentioned in the following part refers to the total communication rate ofτn*N.

4.2 Simulation Results

In our study scenario,the radar transmitter is directly behind the target,which means that the target can be directly illuminated by the radar.At the same time,the communication signal from the base station illuminates the target from the side and is picked up by the radar receiver as it scatters off the target’s surface.We assume that the channel state information has been obtained in advance,as shown in Figure 3,respectively.

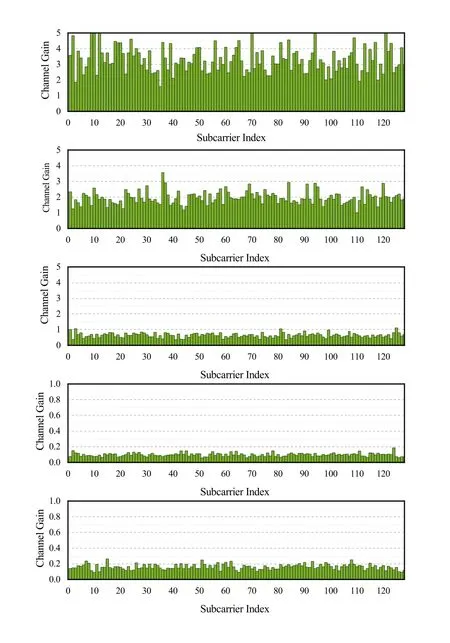
Figure 3.The gain of corresponding channels: From top to bottom,in sequence,they are hc,hr,hd,hcr and hrc.

The convergence of the algorithms is verified first.Figure 4 depicts the average MI of the algorithm our proposed versus the number of iterations for fixed communication rate constraint.It can be seen that our proposed algorithm can converge quickly without long loop iterations.The algorithms for criteria B and C have similar convergence behaviors.

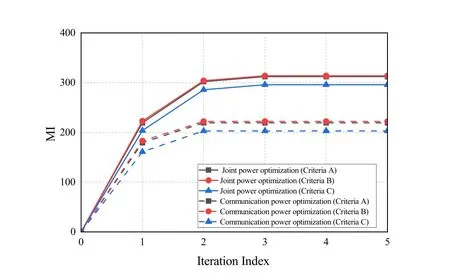
Figure 4.Convergence of the algorithm when communication rate=100 bits/s.

Figure 5 depicts the relationship between the communication rate and the actual transmit power in the system,given a maximum available power of 1200 W for the radar system and 800 W for the communication system.It can be observed that,with the maximum available power of the radar system held constant,as the communication rate increases to a sufficiently high level,the actual transmit power of the radar decreases.In this experiment,when the communication rate exceeds 140 bit/s,the actual transmit power of the radar is reduced.This phenomenon can be attributed to the fact that an increase in communication rate necessitates an increase in communication power.Simultaneously,the communication rate is also influenced by the radar power.When the communication power reaches its maximum available transmit power,the radar power is reduced to mitigate interference and thereby enhance the rate of the communication system.Ultimately,a compromise is reached between the radar and communication systems to satisfy the required communication rate.

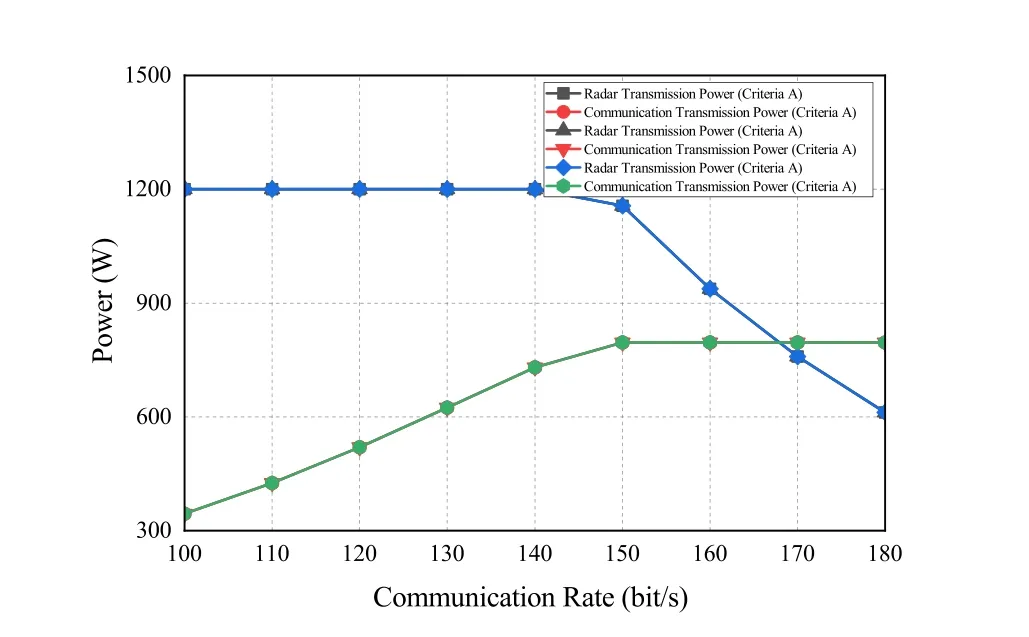
Figure 5.Radar transmission power versus communication rate.

Figure 6 displays the actual transmitted power variation curves of the radar and communication systems when the communication rate constraints are 120 bit/s and 160 bit/s,respectively.From Figure 6a,it can be seen that when the communication rate is 120 bit/s,the radar transmission power and communication transmission power increase synchronously until the communication transmission power reaches its maximum value.Then,to meet the communication rate constraint,the radar transmission power stops increasing,even if there is no maximum available power.This suggests that the maximum available power of the communication system will limit the radar transmission power,and there is a trade-off relationship between them.In Figure 6b,the communication rate constraint is 160 bit/s,and the same conclusion can be drawn that after the communication transmission power reaches its maximum value,it will limit the increase of radar transmission power.

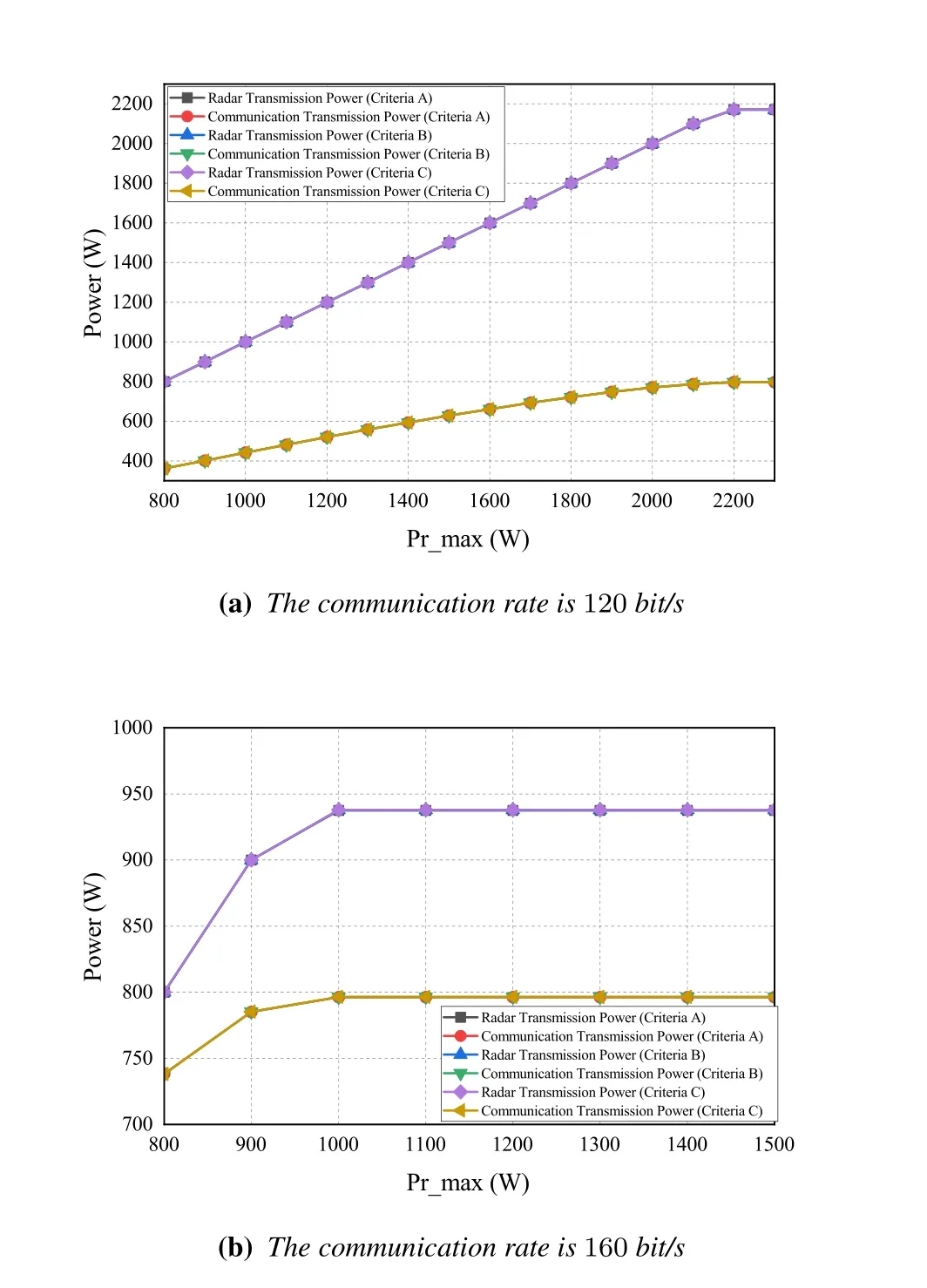
Figure 6.Transmission power versus maximum power in three criteria.

Figure 7 shows the relationship between radar MI and the maximum available transmission power of the radar system.Comparing Figure 7a and Figure 7b,it is evident that an increase in the maximum power of radar subcarriers can enhance radar mutual information.The constraint on communication rate results in an upper bound on radar MI,and as the communication rate increases,the attainable upper bound on radar MI decreases.

Figure 8 shows that as the communication rate increases,the radar MI decreases.In other words,the radar MI is a decreasing function of the communication rate.Both Figure 7 and Figure 8 show that the performance of criteria B is better than that of criteria A and C.This indicates that the signal received by the radar receiver through the target scattering of the communication signal transmitted by the BS is helpful for the radar MI as a useful signal.

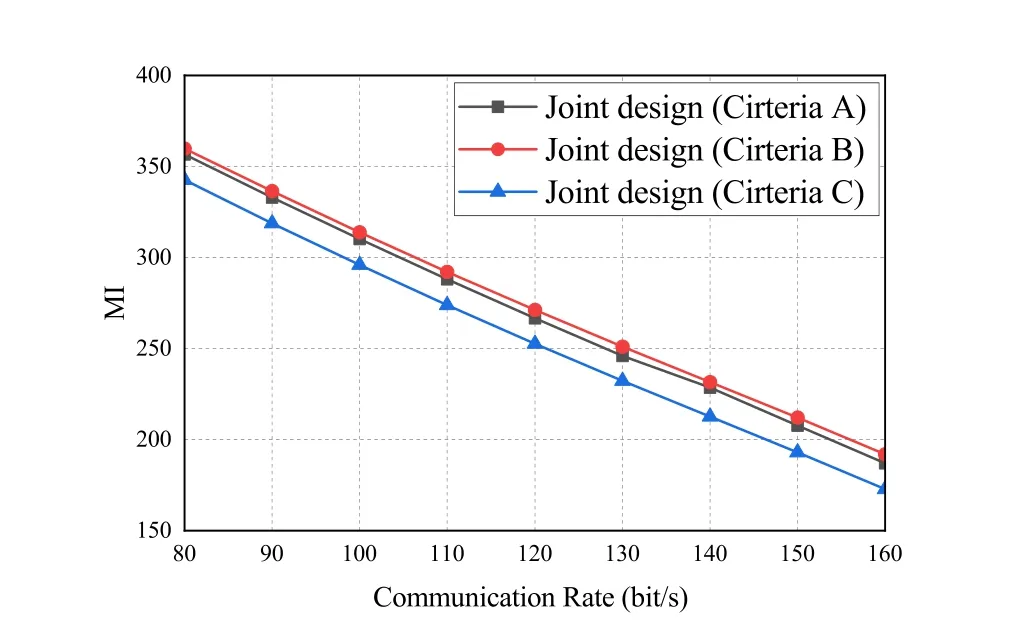
Figure 8.Comparisons of radar MI in three criteria.

We compared the performance of the algorithm proposed in this paper with that of existing algorithms,as shown in Figure 9.Figure 9a,Figure 9b and Figure 9c show the performance of the three algorithms under cirteria A,B and C,respectively.In this paper,we denote the proposed algorithm as the joint design algorithm,and the algorithms used in [14] are denoted as unilateral design.In addition,we consider the performance of the algorithm when the power of the communication system is evenly distributed.It can be clearly seen that the algorithm used in this paper can significantly improve the MI of the radar system.Although when the communication rate increases to a certain extent,the performance of the three algorithms tends to be consistent.This is because the high communication rate causes the radar system to have to reduce its power to meet the communication rate requirements.

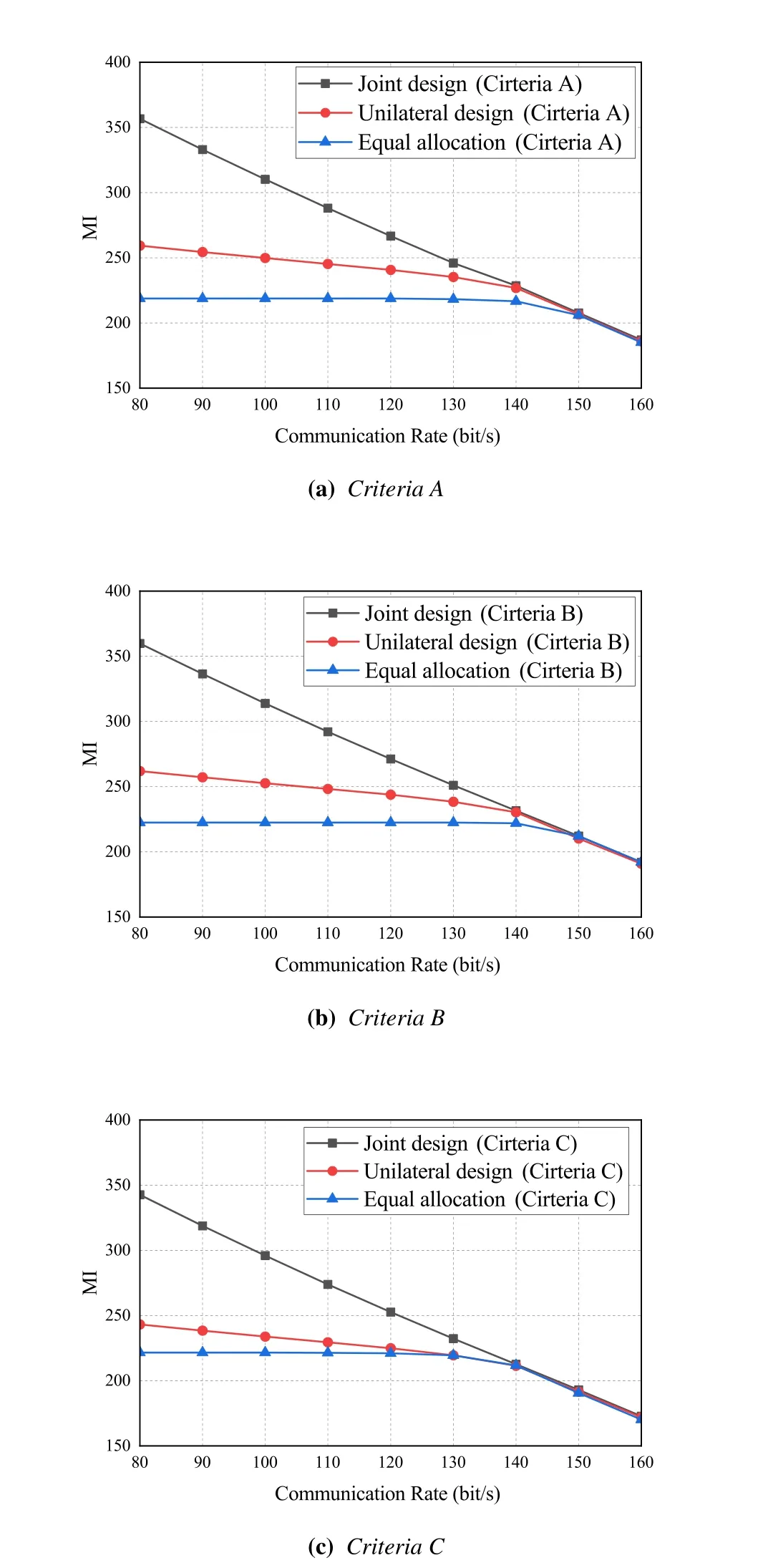
Figure 9.Radar MI versus communication rate in each criterion for different algorithms.

V.CONCLUSION

In this paper,we study the joint power allocation problem of OFDM radar and communication system by maximizing the radar MI subject to constraints on the communication rate and total transmission power.According to the different processing methods of the scattering signal of the communication signal on the target,we propose three radar waveform design schemes based on OFDM.For each scheme,the radar MI is maximized and associated optimization problem is formulated and solved analytically.The numerical simulation results show that the MI of the radar system can be improved by using the scattering signal of the communication system.Moreover,the results also show that,compared with optimizing the power allocation of radar system signal singly,the joint power allocation of communication and radar system can significantly improve the MI of radar.