基于局部信息熵的智能电网数据离群点识别

田 炯，秦发宪，朱 涛

（国网宁夏电力有限公司中卫供电公司，宁夏中卫 755000）

离群点检测问题已引起了数据挖掘领域的广泛关注，并成为众多学者探讨的焦点。离群点指的是一个与其他数据点差别较大的数据点，有可能是不同机制处理后的结果。离散数据点可以反映局部的数据点与整体的数据点之间的差异，有深层的数据内涵，能够表现出优于普通数据的模式，因此在交通运输、识别信贷、分析客户数据等诸多领域有着较为广泛的应用。

众多学者围绕离群点识别展开研究，并涉及多种算法。其中，早期主要偏重于统计算法、距离算法、偏差算法等，如以离群因子作为标准对整体数据进行分析，使其作为整体数据的表征。随着研究的发展，人们在前人基础上提出了一些有效的离群点识别方法，例如文献[1]利用指标计算，满足离群点检测指标；文献[2]利用不同计算处理器的计算资源，基于网格划分的动态方法进行处理，同时定位数据点的空间位置，进行并行离群点检测，实现数据离群点的识别。但上述研究成果重点聚焦静态数据库、低维度数据库，难以处理动态、高维的大数据。

从现有文献来看，关于离群点研究重点集中在低维数据离群点，少有学者基于局部信息熵进行智能电网数据识别，为此，该文以局部信息熵为基础，研究了一种新的智能电网数据离群点识别方法。

1 基于局部信息熵的子空间选取

1.1 选取优选空间

设n维空间集N的特性集，特性集中特定的数据点a在特性集S上的投影为，M(a)为距离半径域，则可得到S的方差定义式为：

其中，VS表示特征集S中特殊点a的方差值[3-4]。

进行阈值设定时，要综合考虑数据所处的空间位置和邻近数据带来的影响，降低阈值设定时的偶然性和片面性，对优选空间的范围进行压缩，得到最佳范围，提高识别方法的可行性[5]。

根据上述方差数据计算公式，可以得到不同数据点的子空间特性集，在不同空间维度上进行比较，得到最优子空间[6-7]。设φ为优质空间集阈值，若满足VS(M(a))≤φ，则可称该空间集为优选空间，对该空间集进行加权处理，便于下一步计算优选空间的信息熵。

1.2 优选空间的信息熵计算

信息熵是用来计算信息稳定性的重要指标，也是检测数据变化特性的重要工具。设W为待检测数据，则有W的信息熵数据为：

其中，E(W)表示信息熵数据的期望值，S(W)表示信息熵数据的取值集合。

根据计算结果可知，E(W) 与数据稳定性呈正比，E(W)数值越大，数据的不稳定性越强[8-9]。再对数据值域进行压缩，据此可以得到局部信息熵值计算公式：

其中，LC(w) 表示局部信息熵值，VS(M(a))max和VS(M(a))min分别表示方差数据值的最大值和最小值，S(w)表示特定集中的特殊数据点。

利用局部信息熵值对数据邻近点进行分析，得到该数据点和其他数据点的投影值，通过无量化处理判断临界点数值，数值越大，则以该数据点为中心的数据排布的不稳定性越大；数值越小，则以该数据点为中心的数据排布越稳定，因此该文选取符合优选空间选取条件的空间范围，减小识别误差[10-11]。从信息熵数值考虑，离群点使数据整体的不稳定性增强，离散程度变大，不确定性越强，因此选择不稳定程度更大的特殊数据点范围作为最优子空间。在选取优选空间，计算信息熵值的基础上，选取子空间，得到最优的子空间范围[12]。

2 智能电网数据离群点识别

2.1 离群状态变化的检索与分析

基于该文提出的识别方法，采用LOF 算法输入样本中的数据，同时输入离散方法和离散点设定阈值，输出得到离群点的空间值[13]。同时分析输出数据，并计算算法的复杂程度，为改进算法统计数据。具体流程如图1 所示。

图1 离群状态变化的检索与分析流程

步骤一：根据样本得到记录集合，进行挖掘处理，去除不符合条件的数据值，以此为下一步数据处理的基础，设其复杂程度为I。

步骤二：根据数据点的数据情况，与邻近的数据进行比较。进而确定邻近数据的空间集合，确定参照对象，设其复杂程度为Ⅱ。

步骤三：确定空间离散方法，设定等区间的限定条件，进行数据离散化处理。利用式（2）和式（3）进行运算，得到数据对象的熵值，设为局部离群因子，设其复杂程度为Ⅲ。

步骤四：根据上述的步骤得到局部离群因子，如果局部离群因子大于设定阈值，则作为输出数据进行计算。

综上，得到总复杂程度Ⅳ，根据得到的复杂程度进行算法演绎，对繁琐的算法过程进行简化处理，识别更加准确的离群点，判断离群点与优选空间值域之间的差别，如果有较大的差别，则证明离群点处于较远位置，具有明显的离群特征[14-15]。

2.2 离群因子计算

智能电网数据离群点识别中，需要进行离群因子的计算，设LEAA1为离群因子e的离群属性，则有：

其中，LEA为离群数据的特征数据，M(e)为上文提到的距离半径域。

得到离群因子的离群属性后，与离群属性阈值进行比较，划分阈值空间，得到断点集合的特征性。过多的断点会导致准确性降低，因此尽量减少断点，以提高识别的精确度，增强方法的聚类能力[16]。设空间邻域集合为：

其中，Y表示邻域集合；p表示邻域对象，p1、p2等表示数据所处位置。则有非空间邻域集合为：

其中，H表示非邻域集合；t表示非邻域对象，t1,t2,…,tn表示数据所处位置。

在对非邻域集合进行离散化处理后，就可以得到一个特定的概率，表示非空间属性的概率值，如下式所示：

其中，ζ为属性系数；R为所得概率，H(t)max和Y(p)max分别为集合中最大数值。

得到概率之后进行筛选，通过挖掘处理确定概率更大的非空间属性值，对概率较小的非空间属性概率值进行删除处理，增强算法对冗余数据的甄别能力，完成划分过程。

2.3 检测智能电网数据离群点的变化

更新数据时，如果不对原始数据进行处理，就会对个别数据产生影响，进而影响整体数据，使最终结果产生较大偏差。因此在插入和删除智能电网数据时，要对智能电网数据离群点的变化进行检测。

当删除数据时，需要重新计算剩余离群点数据。当数据点b从集合G中删除时，若数据点满足式（8）时，直接删除该数据，无需进行其他处理。

其中，c表示离群点数据标准值；u表示标准差值；k表示离群点相邻数据；Ai表示离群因子e的离群属性。

当增加数据时，若同样满足式（8），则可直接添加数据到值域中；不满足式（8）时，需要将最远端的数据进行删除处理，然后计算剩余数据平均值，并求出添加数据点与相邻数据点的差值，以平均值计入值域，根据平均值实现离群点值域识别。

3 实验研究

为了验证该文提出的基于局部信息熵的智能电网数据离群点识别方法的实际应用效果，设定实验。实验环境如图2 所示。

根据图2 可知，该文提出的实验环境核心设备为MCP2510 控制器，通过通信模块、显示模块、输入输出接口电路模块和芯片内部测试模块设定实验环境。实验过程中，工作电压为200 V，工作电流为150 A，选用的操作系统为Windows10 系统。

选用该文提出的离群点识别方法和传统的文献[1]基于评价指标的离群点识别方法和文献[2]并行检测的离群点识别方法进行实验对比，分别计算识别准确率和识别效率。

识别准确率计算如式（9）所示：

其中，Z表示识别准确率；d表示识别的正确数据；l表示识别的错误数据。

识别效率计算过程如式（10）所示：

其中，M表示识别效率；R表示时间T内识别的数据量。实验识别的离群点如图3 所示。

图3 识别离群点

根据式（9）计算识别准确率，得到的实验结果如图4 所示。

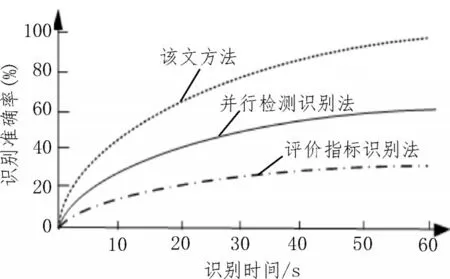
图4 识别准确率实验结果

根据图4 可知，随着识别时间的增加，三种识别方法的识别准确率都在不断提高，该文提出的识别方法识别准确率高于传统识别方法，当时间为60 s时，准确率可以达到95%以上。造成这种现象的原因是该文方法识别的过程中，能够围绕局部信息熵进行子空间选取，在一定程度上弥补了现有离群点检测方法的缺陷，同时为离群点现实应用提供了有力且清晰的参考数据。

识别效率实验结果如表1 所示。

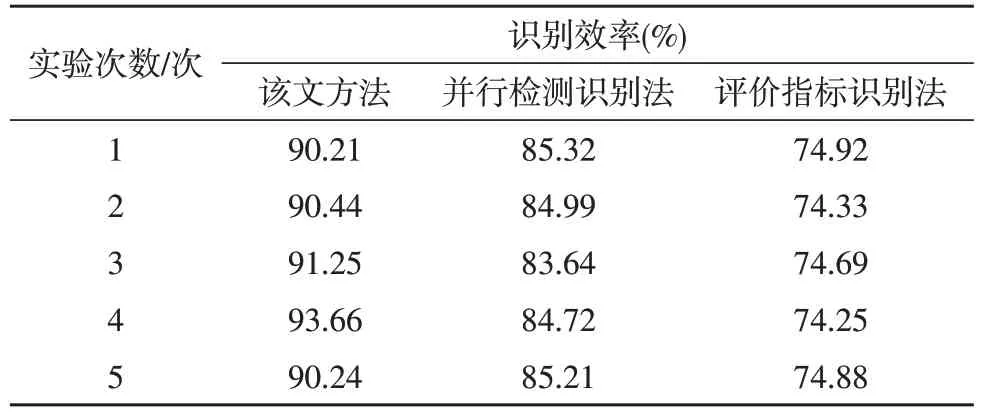
表1 识别效率实验结果

根据表1 可知，该文提出的识别方法识别效率始终在90%以上，具有极强的识别能力。

综上所述，该文方法研究结果通过选取智能电网数据离群点所属的子空间，并在其中计算信息熵，检索与分析离群子状态，计算离群因子，识别离群点的变化并更新数据，进行重新处理后，数据更贴近设定算法的要求，提高了计算准确性。

4 结束语

该文基于局部信息熵提出一种新的智能电网数据离群点识别方法，通过选取局部信息熵子空间、智能电网数据离群点识别两个步骤确定智能电网数据离群点识别的关键因素。研究表明，该文的识别方法具有极强的识别能力，能够为离群点检测提供切实的参考依据与方向启示。但是该文方法也存在一定不足，主要表现在选取优秀子空间计算信息熵过程中计算难度大，且计算结果易与实际结果存在偏差，检索分析计算离群因子步骤较为烦琐，不利于连续数据的深度剖析。