用于新能源发电的新型升降压转换器及其控制策略

罗 朋, 陈光浩, 杨东红, 郭 磊

(广东海洋大学 电子与信息工程学院,广东 湛江 524088)

由于能源、环境问题的日益突出,太阳能、波浪能和风力发电等新能源发电得到广泛应用[1],然而新能源发电装置受环境因素影响大,普遍存在输出电压变化大的问题[2],难以实现能量的储存。升降压转换器由于同时具有升压和降压能力,适用于新能源发电装置的储能。传统升降压转换器因寄生参数影响,在极端占空比下运行时,效率会大大降低,电压应力很大,难以工作在较宽范围的输入电压下。同时其输入电流不连续,输入电流纹波大。因此,更宽的转换比和输入电流连续成为解决问题的关键。

Banaei等[3]、Miao等[4]、Banaei等[5]、Li等[6]及李梦娇等[7]通过加入储能单元和开关器件获得更宽的转换比,但其输入电流不连续。交错型转换器[8]在低压应力下可以实现高升压或降压转换比,但控制策略复杂。Bahrami等[8]、Hsieh等[9]、Hasanpour等[10]及荣德生等[11]采用耦合电感结构,通过调节匝数比使电路获得更高升压比和降压比,但其开关管数量多,开关损耗大。Zhang等[12]和Kumar等[13]提出了单管的升降压转换器,在实现更宽转换比的同时,也能实现输入电流连续,但其开关管电压应力大。

升降压转换器通常采用传统的PI 控制,但是在某些应用场合,如输入电压变化较大时,传统的PI 控制往往无法获得满意的系统动态和静态控制性能,甚至会出现系统不稳定运行的现象。Li等[14]、Yang等[15]及周坤雨等[16]提出了预测控制、滑模控制等控制策略,这些策略能提高升降压转换器的输出动态响应的速度,但是不适用于存在较大输入扰动的情况。前馈算法通过对输入电压的采样,可以抑制输入电压扰动对输出电压的影响,能够有效改善转换器的输入暂态响应[17]。

本文提出了一种新型升降压转换器。使用耦合电感获得更宽的转换比,为提高效率,由电容和二极管组成的无源钳位电路回收漏感能量,抑制漏感造成的开关管电压尖峰,使得输入电流连续。设计了一种PI控制器结合前馈控制策略,实现转换器在整个输入电压范围内良好的输入暂态响应。这种控制策略能使转换器稳定工作在新能源发电装置储能场景。

1 转换器模态分析

所提出的升降压转换器的等效电路如图1所示,由二极管D1、D2、D3、电感L1、耦合电感、电容C1和Co、开关管S组成。为了便于转换器分析,电容C1和Co足够大,VC1和VCo在一个开关周期内可视为恒定电压;耦合电感的匝数比定义为Np∶Ns=1∶n。转换器在连续导通模式(continuous conduction mode,CCM)下工作,主要波形和能量流动分别如图2和图3所示。在一个开关周期内,转换器主要有4个工作模态,各模态的主要工作过程如下。

图1 所提转换器等效电路

图2 所提转换器的主要波形

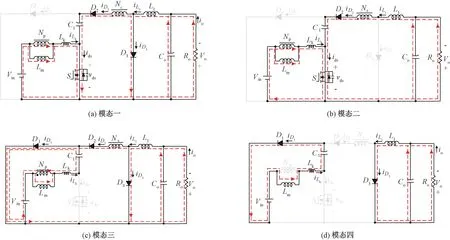
图3 转换器的4种工作模态

模态一(t0～t1,图3(a)):S、D2、D3导通,D1截止。Vin为耦合电感一次侧充电,iLk增加。电感L1通过D3为负载提供能量,C1与耦合电感二次侧为负载和L1充电,iD3减小。当iD3减小为0时,此模态结束。

模态二(t1～t2,图3(b)):S、D2导通,D1、D3截止。Vin为耦合电感一次侧充电,iLk增加,C1和耦合电感二次侧为负载和L1充电,iL1增加。当开关管S关断时,此模态结束。

模态三(t2～t3,图3(c)):S关断,D1、D2、D3导通。Vin和耦合电感一次侧为C1充电,iLm线性下降。耦合电感二次侧与L1为负载供电,iL1持续减小。当iLm等于iLk时,D2截止,此模态结束。

模态四(t3～t4,图3(d)):S关断、D2截止,D1、D3导通。Vin和耦合电感一次侧为C1充电,iLm减小。L1为负载供电,iL1下降。当开关管S导通时,此模态结束。

2 稳态分析和比较

2.1 电压转换比

为了简化分析,模态一和模态三是由于漏感Lk引起的,时间很短,只考虑模态二和模态四。

在图3(b)的0～DT期间,根据基尔霍夫电压定律(KVL),推导出的方程式为

VLm=Vin;

(1)

VL1=VC1+nVLm-VCo。

(2)

在图3(d)的DT～T期间,方程表示为

VLm=VC1-Vin;

(3)

VL1=-VCo。

(4)

根据式(1)和式(3),由Lm的伏秒平衡可得

(5)

根据式(1)、(3)、(4),由L1的伏秒平衡可得

(6)

由式(6)可得,转换器的电压转换比为

(7)

图4展示了在不同匝数比n的情况下,电压转换比M与占空比D的关系曲线,当占空比一定时,匝数比越高,电压转换比越高。

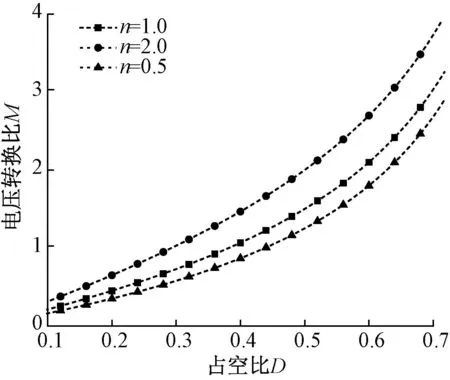
图4 不同匝数比下电压转换比与占空比之间的关系曲线

2.2 电压电流应力分析

根据图3(b)和图3(d)可以推导出开关管和二极管的电压应力如下:

(8)

(9)

(10)

从图3(b)中,根据基尔霍夫电流定律(KCL),可推导出以下关系:

iCo=io-iL1;

(11)

iC1=iL1=iD2。

(12)

从图3(d)中,根据KCL,可推导出以下关系:

iC1=-iLm=-iD1;

(13)

iCo=iL1-io;

(14)

iD3=iL1。

(15)

根据式(11)和式(14),由电容Co的安秒平衡可得

(16)

由图3(b)可推导出电感L1的纹波如下:

(17)

由式(16)和式(17)可得L1的电流最大值和最小值为

(18)

(19)

根据式(12)、(13)、(16),由电容C1的安秒平衡得到ILm为

(20)

根据图3(d),Lm的纹波表示为

(21)

由式(20)、(21)可得Lm的电流最大值和最小值为

(22)

(23)

根据图3(b)和3(d)以及式(16)和式(20)可以推导出开关管和二极管的电流应力如下:

ID1=ID2=DIo;

(24)

ID3=(1-D)Io;

(25)

(26)

2.3 功率器件设计

在边界导电模式(boundary conduction mode,BCM)下,输出电流为IoB,根据式(19)和(23)可以得到电感L1与Lm为

(27)

(28)

假设C1和Co的电压纹波为ΔVC1和ΔVCo,fs为开关频率,电容的计算公式为

(29)

根据式(4)、(11)、(12)、(16),电容C1、Co应该满足以下条件:

(30)

(31)

2.4 性能对比

如表1所示,本文对单开关管结构的转换器与所提出转换器进行了性能对比。与文献[6]中的转换器相比,所提转换器输入电流连续,开关管电压应力低,能够降低输入电流纹波和开关管开关损耗;与文献[13-14]中的转换器相比,所提转换器组件总量数少,开关管电压应力低,具有成本低和效率高的优点。

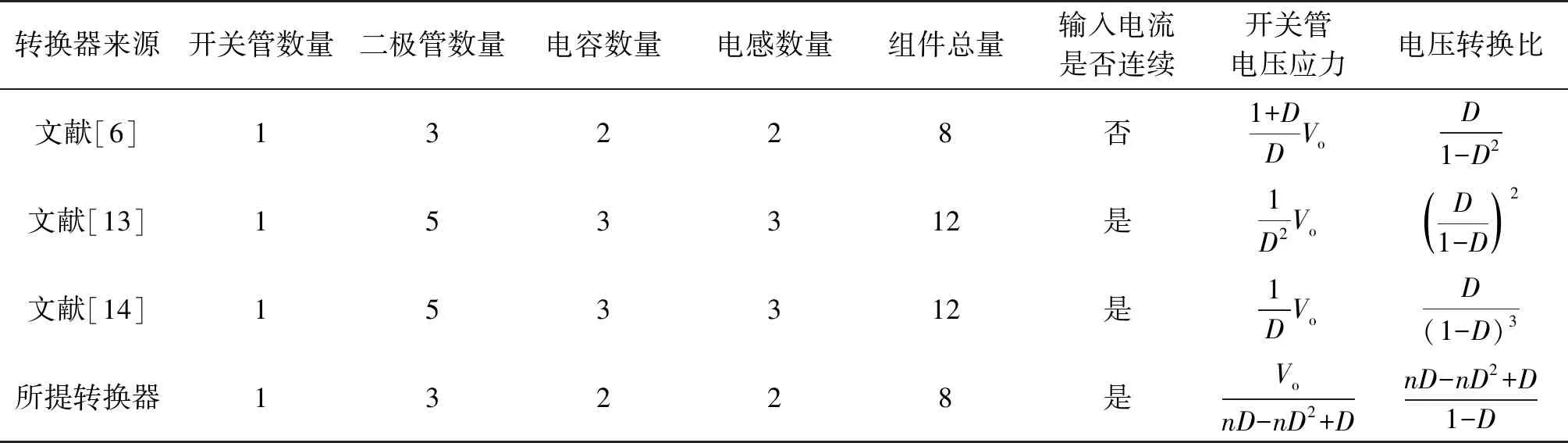
表1 转换器性能对比

3 转换器控制策略

3.1 小信号建模

小信号建模被用来推导后续控制的开环传递函数,本小节提供了所提出的转换器的小信号推导和分析,利用开环传递函数推导出合适的PI参数。为了简化CCM模态下该转换器的小信号模型分析,在分析过程中只考虑模态二和模态四,将状态向量定义为

(32)

(33)

并且输入向量定义为

u=[vin]。

(34)

在0～DT时间段,根据图3(b)可以得到以下状态矩阵:

(35)

在DT～T时间段,根据图3(d)可以得到以下状态矩阵:

(36)

状态平均方程如下:

(37)

根据式(33)、(34)、(35)、(36)、(37)可得空间状态平均矩阵如下:

(38)

状态变量、输入变量和控制变量可以用小信号干扰变量描述为

(39)

式中:IL1、ILm、Vin、VC1、VCo、D分别为iL1、iLm、vin、vC1、vCo、d的平均值。占空比到输出的传递函数如下:

(40)

式中:M0=R(1-D)2;M1=(L1(1-D)2-D2Lm);M2=R(CoL1(1-D)2+Lm(CoD2-C1));M3=C1L1Lm;M4=C1CoL1LmR;N0=R(1-D)2((1-D)2+1);N1=D2Lm(Dn-1-n);N2=-LmC1R((1-D)2n+1-D)。

3.2 PI控制器设计

为了使转换器工作能够稳定运行,在小信号模型的基础上进行PI控制器的设计,PI控制器的传递函数定义为

(41)

闭环传递函数GClose-Loop(s)表示为

GClose-Loop(s)=GVod(s)Gc(s)。

(42)

根据式(41)和式(42),采用工程近似法对Kp、Ki进行取值,Kp为0.000 78,Ki为0.001。升压模式下闭环伯德图如图5(a)所示,降压模式下的闭环伯德图如图5(b)所示。图5说明了在PI控制器的作用下,转换器在升压与降压状态下工作稳定状态均稳定。

图5 加入PI控制器后的环路增益伯德图

3.3 PI控制器结合前馈控制策略

根据输入采样电压和输出给定电压计算转换器占空比的前馈算法,通过小信号建模得出PI参数,使转换器在升压和降压模式下稳定输出电压,控制框图如图6所示。

图6 闭环控制框图

4 损耗分析

转换器的效率受到寄生参数的影响。rL1、rLp、rLs、rC1及rCo分别表示电感L1、耦合电感一次侧、耦合电感二次侧、电容C1和Co的等效电阻。rds为开关管S的导通电阻,rD1、rD2和rD3分别为二极管D1、D2和D3的导通电阻,VF1、VF2和VF3分别为二极管D1、D2和D3的导通压降。

4.1 电感损耗

根据式(16)和式(20)可得L1、耦合电感一次侧和二次侧电流有效值为

(43)

(44)

(45)

根据式(43)、(44)、(45),总电感损耗为

(46)

4.2 电容损耗

根据式(13)、(14)、(16)、(20)可得电容C1和Co的电流有效值为

(47)

(48)

电容总损耗为

PC=IC1(rms)2rC1+ICo(rms)2rCo。

(49)

4.3 开关损耗

开关管损耗主要为rds引起的导通损耗以及上升时间tr和下降时间tf引起的开关损耗,根据式(26)可得开关管S的电流有效值为

(50)

开关管的导通损耗为

PS-C=Ids(rms)2rds。

(51)

开关管的开关损耗为

(52)

4.4 二极管损耗

二极管的损耗主要为导通损耗和开关损耗,根据式(24)和(25)可得二极管D1、D2和D3的电流有效值为

(53)

(54)

(55)

二极管的开关损耗可表示为

PD-S=VF1ID1+VF2ID2+VF3ID3。

(56)

二极管的导通损耗可表示为

(57)

根据式(48)、(49)、(51)、(52)、(56)、(57),转换器的总损耗为

PLoss=PL+PC+PS-C+PS-S+PD-C+PD-S。

(58)

假设Po为转换器的输出功率,则转换器效率为

(59)

5 实验验证

为了验证转换器和PI控制器结合前馈控制策略的可行性,表2给出了所提转换器的样机参数,实验样机实物如图7所示。图8展示了实验样机的实物测试图,其中直流电源型号为TH6900,直流负载型号为IT8513B+,示波器型号为WaveSurfer 4054HD,驱动芯片型号为TMS320F28335,电压探头型号为DP6150,电流探头型号为HCP8030。

表2 样机参数

图7 实验样机实物照片

图8 实物测试照片

在满载情况下,图9展示了所提转换器升压和降压2种模式下的实验波形。由图9(a)和9(d)可以看出,开关管在升压和降压情况下电压被钳位,说明漏感回收电路起作用。由图9(c)和9(f)可以看出iLk在升压和降压情况下是连续的,输入电流等于iLk,转换器输入电流连续。图9中的实验波形与图2所展示的波形图基本一致,开关管电压应力Vds在升压模式下为55 V,在降压模式下为88 V。

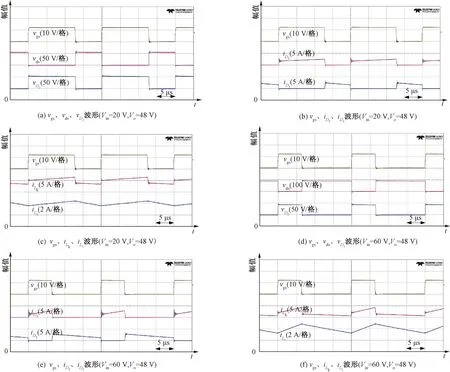
图9 满载情况下的实验波形

图10展示了所提转换器在输入电压最大值为60 V,最小值为20 V,呈方波规律变化下加入前馈控制前后输入扰动对比测试实验波形。图10(a)展示了未加前馈的输入扰动测试波形,输出电压峰值达到72 V,超调量达50%;图10(b)展示了加入前馈控制的输入扰动测试波形,输出电压尖峰仅为50 V,超调量仅为4.2%,可见加入前馈控制提高了转换器的稳定性。图11(a)、11(b)分别展示了20 V和60 V输入电压、48 V输出电压,输出功率从半载变到满载再变回半载的扰动测试,输出电压稳定在48 V,说明所设PI参数能使所提转换器具有良好的输出暂态响应。

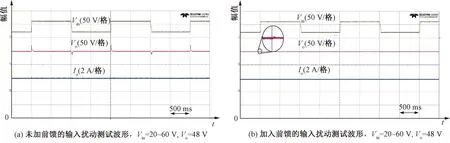
图10 加入前馈控制前后输入扰动对比测试

图11 输出功率的扰动测试

图12为转换器升压模式和降压模式分别在不同功率下的效率曲线,满载测量效率分别为92.80%、96.03%,最大测量效率分别为97.08%、97.10%。

图12 升压和降压模式下实测效率曲线图

图13展示了满载下转换器分别在20 V和60 V输入电压,48 V输出电压的计算损耗分布,升压模式总损耗为6.84 W,降压模式总损耗为3.38 W。

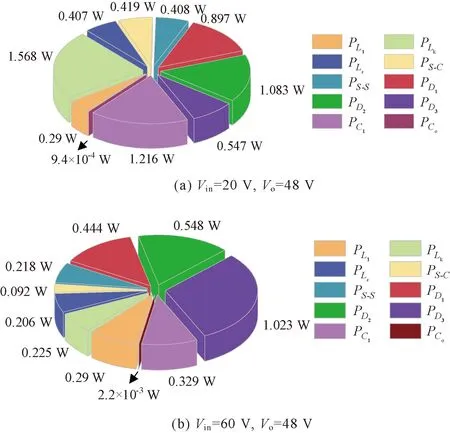
图13 满载情况下升压和降压模式计算损耗分布

7 结论

针对新能源发电装置,本文提出一种基于PI 控制器结合前馈控制的新型单管耦合型升降压转换器。详细分析了转换器的工作原理,比较了相关转换器的性能,设计了转换器的控制策略。实验结果验证了转换器理论分析的可行性,所提控制策略改善了转换器对输入电压突变的响应特性。转换器升压满载测量效率为92.80%,最大效率为97.08%;降压满载测量效率为96.03%,最大效率为97.10%。