材料掺量对塑性混凝土抗压强度影响分析
王蓓蓓,宋 力,高玉琴
(1.华北水利水电大学水利学院,郑州 450046;2.黄河水利委员会黄河水利科学研究院,郑州 450003;3.水利部堤防安全与病害防治工程技术研究中心,郑州 450003)
0 引言
塑性混凝土是用膨润土、黏土等部分代替水泥的柔性材料。与普通混凝土相比,具有低强度、低弹性模量、渗透系数小等特点,因此其具有抗压能力弱、变形能力强、抗渗性能好等特性,多被用作水工防渗墙的建造材料。
目前有关塑性混凝土配合比的研究多为定性描述指标随某因素的变化趋势,或只考虑了单一变量的影响,没有定量分析多种因素的共同作用。因此,本文定量分析多因素作用下塑性混凝土抗压强度变化规律,为试配性能良好的塑性混凝土提供参考。
1 研究内容
此研究的数据来源于吴为健的《塑性混凝土配合比设计小结》,文章对不同的砂率、水胶比、膨润土掺量排列组合,固定用水量、粉煤灰掺量、减水剂掺量,并以坍落度为控制指标设计了12组配合比。试验得到了塑性混凝土的强度、弹性模量、模强比、渗透系数等指标,并分析了砂率、水胶比、膨润土掺量与弹性模量的相关性。
此研究基于文献[3]的塑性混凝土受压试验的数据,使用了灰色关联分析、回归分析、sobol 法这三种方法,研究影响塑性混凝土受压力学性能的各因素的重要程度,提出了抗压强度与水胶比、砂率、膨润土掺量的关系模型,研究成果可为塑性混凝土的配合比设计提出合理建议。
2 研究方法
不同方法的分析效果有所不同,应结合数据特点,选择合适的方法。传统的研究影响因素敏感度分析的方法需要大量样本,具有一定的局限性。此文的试验数据有限,故选用能够分析少量样本的灰色关联方法、对样本数量无较高要求的回归分析法、可以使用sobol squence 生成样本的sobol 法进行研究。
此研究分为三个阶段:第一阶段,根据试验数据进行灰色关联分析,得出各变量在该指标下的灰色关联度,灰色关联度越大说明该因素对指标的影响越大。第二阶段,选取灰色关联度较大的因素作为自变量,采用控制变量法,秉承单一变量原则,使用origin 作图,初步拟合出抗压强度随自变量的变化曲线;根据因变量与自变量的关系形式,选用合适的模型对抗压强度(因变量)与材料掺量(自变量)进行拟合,并根据拟合优度的大小判断拟合程度的优劣。第三阶段,用敏感性分析中的sobol 方法,计算上一步得出的模型参数的敏感度,结合实际,分析该模型的正确性及意义。
2.1 灰色关联分析
灰色关联分析是一个对系统发展变化态势的定量描述和比较的方法,与传统的分析方法不同,它对样本数据的数量、规律性等没有过多要求,计算简便且计算结果与定性分析结果一般较为相近。因此,对于本文的十二个样本数据,选用灰色关联分析法对其进行初步分析,具体步骤为:①确定参考序列;②无量纲化;③计算差异变换矩阵;④计算灰色关联系数;⑤计算灰色关联度;⑥关联性好坏的评判
2.2 回归分析
回归分析是研究多个变量间相互作用关系的一种分析方法,通过建立回归模型,量化自变量与因变量之间的关系,从而由不同的自变量取值预测因变量的值。根据灰色关联分析的结果,将灰色关联度较大的因素作为自变量,对其进行回归分析,具体步骤为:①确定自变量和因变量;②绘制散点图,观察因变量随自变量的变化趋势;③计算出模型参数,建立回归模型;④根据拟合优度R2的大小判断拟合效果。
2.3 Sobol法分析
此研究参数整体对输出结果的影响,故选取全局敏感性分析中最常见的基于方差分解的sobol 方法。Sobol 指数法基于方差分解的原理,具有对单个参数的主效应、全效应及多个参数的交互效应进行分析的优点,但该方法计算量较大,故本文使用matlab 对回归分析所得模型进行敏感性分析,具体步骤为:①利用sobol sequence 生成样本;②将回归分析得出的模型带入到sobol 算法中进行运算,得出各参数的一阶影响指数与总效应指数;③对结果进行分析,得到各参数的敏感性水平。
3 结果与分析
3.1 灰色关联分析结果
①根据目标需求,将力学性能指标:抗压强度组成的序列作为参考序列;将影响因素:砂率、水胶比、膨润土掺量组成的序列作为比较序列。为了提高计算效率、简化计算步骤,本文借助matlab计算灰色关联度。
②调用数据,运行程序,可得差异变换矩阵:
式中:两级最小差a=0.0051;两级最大差b=0.4388
③子序列中各个指标与母序列的关联系数为:
④序列中各个指标的灰色关联度分别为:0.6817 0.6987 0.6906
⑤对运行结果进行分析:砂率、水胶比、膨润土掺量的灰色关联度分别为0.6817、0.6987、0.6906,灰色关联度从大到小依次为水胶比、膨润土掺量、砂率。三者灰色关联度大小相近,且均大于0.6,说明三者与抗压强度的关联程度较大,即三者对抗压强度均有较大影响。为了进一步探究三者与强度的关系需进行更深入的分析。
3.2 回归分析结果
①根据目标,确定自变量为砂率、水胶比、膨润土掺量,且自变量间相互独立;因变量为抗压强度,且自变量与因变量存在相关关系。
②利用origin分别绘制三者与抗压强度的散点图,可推测出抗压强度随砂率、水胶比、膨润土掺量的增加而近乎呈线性降低趋势,即因变量随自变量的增加呈线性变化。
③由上述分析可知因变量与自变量为线性关系,故可对其进行多元线性回归分析。本文借助matlab 中的regress 函数计算出线性回归模型的参数,可得出砂率x1、水胶比x2、膨润土掺量x3与抗压强度y 的关系式为:
y=-0.058x1-15.0959x2-0.06x3+25.4523……(1)
由自变量的系数绝对值大小,判断该变量的改变对结果的影响程度:系数绝对值越大,影响程度越高,反之则越低。因此,水胶比的改变对抗压强度的影响最大,膨润土掺量与砂率的改变对抗压强度的影响都处于较低水平。
④根据输出的stats(检验回归模型的统计量)中的拟合优度对拟合效果作出判断:拟合优度越接近1,回归直线对观测值的拟合程度越好。该回归模型的拟合优度R2=0.9956,拟合效果良好。
⑤将由回归模型得到的抗压强度计算值与实测值进行对比(如下表1所示),进一步检验拟合效果的优劣。由该表可以看出,模型计算出的抗压强度值与实测的抗压强度值的相对误差的绝对值范围在0.10%~1.55%,说明该模型是合理的且拟合精度高。
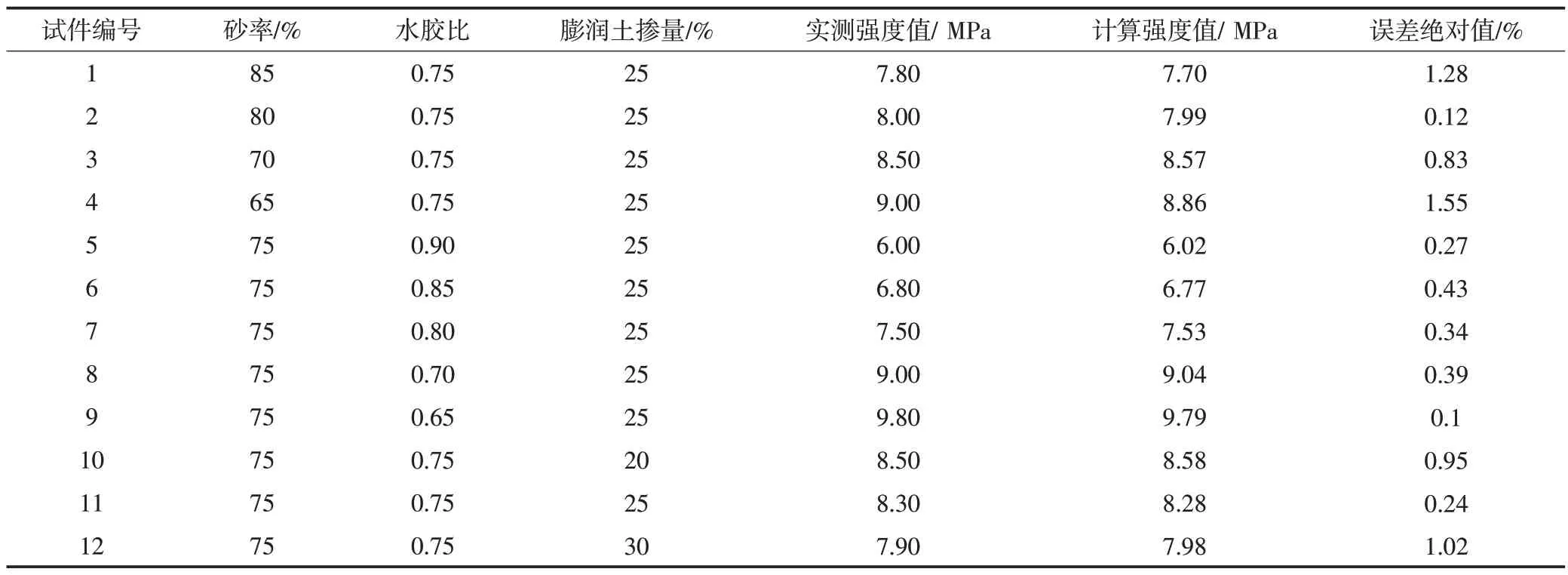
表1 各配合比抗压强度实测值与计算值对比表
⑥绘制实测强度、计算强度、误差百分比的折线图(如图1所示),图中直观的展示出实测值与计算值的曲线近乎重合,说明两者差值极小。
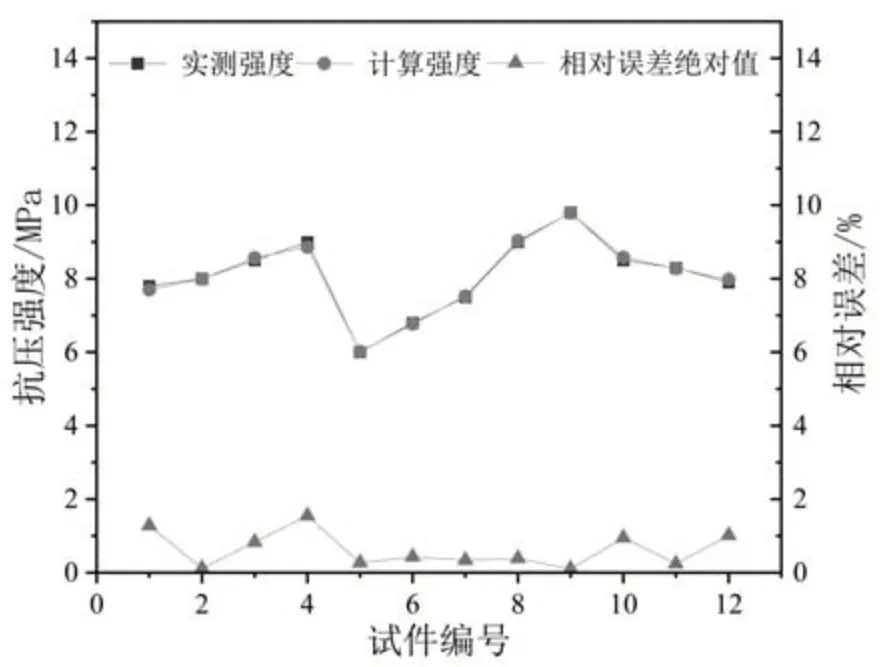
图1 实测强度与计算强度对比
⑦对同种原材料、相同的实验条件下,可以由该模型根据设定的水胶比、砂率、膨润土掺量的数值,推算出该配合比下混凝土试块的抗压强度值;同时也可由目标强度,利用该模型调整配合比以达到要求。
3.3 Sobol法分析结果
①随着采样点个数的增加,结果趋于稳定,然而采样点个数越多,运行程序所需时间越长。因此,需调整样点个数,选取合适的参数水平,观察结果,发现当npoop(样本数量)=200时,样点基本稳定。
②根据上一步分析结果,将回归模型y=-0.058x1-15.0959x2-0.06x3+25.4523编入子程序。
③运行sobol 算法,调用子程序,分析模型中参数的敏感性,得出结果:
一阶影响指数:-0.0004、1.0376、-0.0001
总效应指数:0.0000、0.9976、0.0000
该结果表明在目标函数y=-0.058x1-15.0959x2-0.06x3+25.4523下,参数水胶比的总敏感度显著高于其它模型参数,参数水胶比最敏感,它的改变对输出项的影响最大。砂率与膨润土掺量的敏感度极低,说明对于抗压强度影响因素来说属于非敏感性参数。该结果与回归分析所得结论一致。
4 结语
综上所述:对数据进行灰色关联分析,计算得出砂率、水胶比、膨润土掺量这三个因素的灰色关联度分别为0.6817、0.6987、0.6906,分析可知:水胶比的关联度最大,砂率、膨润土掺量的关联度略小,三者均与抗压强度有较好的关联性。为了进一步探究强度与砂率、水胶比、膨润土掺量的关系,对数据进行回归分析,得到数学模型,并由系数绝对值大小可知水胶比的改变对抗压强度的影响远大于膨润土掺量与砂率,且该模型可用于相同条件下抗压强度值的预测或配合比的调整。最后,使用sobol法对模型进行敏感度分析,证实了水胶比最为敏感,膨润土掺量与砂率属于非敏感性参数。
——与非适应性回归分析的比较

