保温时间对钛合金板翅式换热器真空钎焊过程温度场及残余应力的影响

李悦，王建峰，马龙飞，杜春辉，胡凤娇，占小红,

(1.南京航空航天大学,南京,211106；2.中国机械总院集团北京机电研究所有限公司,北京,100083)

0 序言

板翅式换热器是1种新型高效换热器，因结构紧凑轻巧且能适应多种流体间的换热，广泛应用于航空、航天、船舶等领域[1-2].传统铝合金、铜合金和不锈钢等材质已不能满足更高端的换热器性能，高效钛合金板翅式换热器正逐渐成为研发热点[3-5].钎焊是钛合金板翅式换热器制造流程中最为重要的一环，其质量往往决定了板翅式换热器的力学性能及服役寿命[6-9].在钎焊技术方面，目前钛合金板翅式换热器成品率较低、残余应力及变形较大，相应的高效高可靠钎焊技术还需进一步突破.

特别是针对轻型钛合金钎焊工艺，其材料厚度通常在0.08～ 0.1 mm，材料越薄，翅片的支撑力和强度越差，在1 250 K以上真空炉内材料的金属相变更大，造成材料变形、变脆等问题.真空钎焊炉内的物理化学变化较为复杂，涉及材料与炉体间的热对流及热辐射、钛合金板材的相变及热膨胀、钎料的润湿铺展及熔蚀等过程[10].因此，在钎焊过程中，特别是钎缝附近易出现应力集中现象，这将直接影响接头的综合性能.若能定性定量的了解钛合金板翅结构真空钎焊时的钎料流动过程，明晰应力集中及变形的产生原因，即可精准调控真空钎焊接头性能，实现真空钎焊工艺流程设计的参数化.为此，利用数值模拟技术对钛合金板翅结构真空钎焊过程建模与求解，从而预测真空钎焊接头的温度场以及应力变形分布具有很重要的应用前景.

在钎焊过程的建模与仿真方面，国内外学者做了大量的工作，提出并改进钎焊过程数值仿真模型.罗冲等人[11]采用流体体积法对换热器中十字钎角的成形过程进行了数值模拟研究，并分析了钎焊温度、钎缝间隙等因素对钎缝成形的影响.综上所述，针对真空钎焊过程仿真研究，国内外学者多基于传热学理论建立温度场仿真模型开展真空炉内温度均匀性研究，对钛合金板翅结构钎焊的仿真研究较少.钎焊温度精度和均匀度直接决定焊接温度场均匀性，是保证大尺寸复杂构件钎焊质量的重要因素.尤其对于复杂构件而言，温度场局部过高、过低都会导致该区域钎焊接头连接质量降低，成为薄弱环节，所以明确钎焊温度场的分布对实现钛合金的高质量连接尤为重要.该文通过采用有限元方法研究钛合金板翅结构真空钎焊过程的温度场以及焊后残余应力分布，对比研究不同钎焊时间对残余应力分布的影响并分析其机理.

1 试验方法

1.1 母材及钎料

选用膏状Ti-Zr-Cu-Ni钎料开展TA1钛合金板翅式换热器结构真空钎焊试验研究，其化学成分如表1所示.板翅式换热器结构试验件如图1所示.

表1 TA1钛合金和Ti-Zr-Cu-Ni钎料的化学成分(质量分数，%)Table 1 Chemical composition of TA1 and Ti-Zr-Cu-Ni solder

换热器芯体是由大量板翅结构单元组成，且这些结构单元在空间上具有明显的周期性、对称性.因此，该文截取了如图1(a)所示的80 mm × 40 mm的结构单元试验件开展相关真空钎焊试验研究，翅片几何尺寸如图1(b)所示.

1.2 试验设备与方法

该文采用的真空钎焊设备为ZGS-120真空炉，利用压力机构对工件进行夹持，并在真空度小于8 × 10-3Pa的环境中进行钎焊连接，以保证钎焊质量.在钛合金翅片结构试验件真空钎焊之前，需对试验材料进行焊前预处理.该文设计的钎焊工艺如图2所示，钎焊温度T=1 150 K，保温时间t=20 min，并随炉冷却至室温.

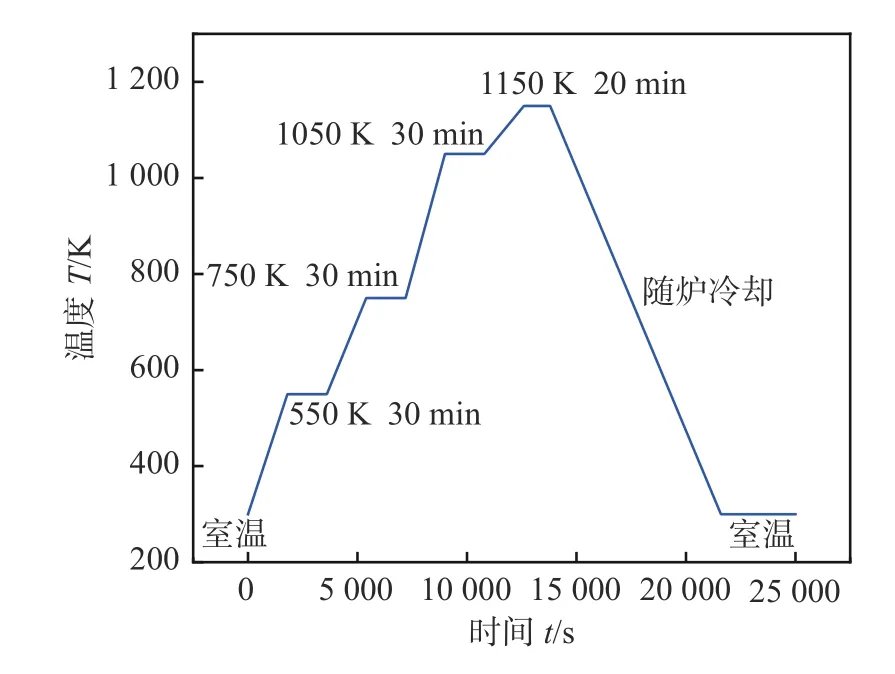
图2 真空钎焊工艺温度曲线Fig.2 Vacuum brazing process temperature curve

1.3 模型建立

1.3.1 几何模型建立与网格划分

该文利用COMSOL软件建立1/4对称模型作为计算域，如图3所示.忽略炉膛几何，仅保留加热带几何作为钎焊热源.为提高计算精度，在进行网格划分时，对翅片网格进行细化，特别是钎缝处易出现应力集中需要对该处网格进一步细化.而加热带仅参与温度场计算，因此加热带网格适当粗化，以减少网格数量及自由度数，节约计算资源.最终得到的计算网格单元总数为13 267，求解自由度数为34 340.

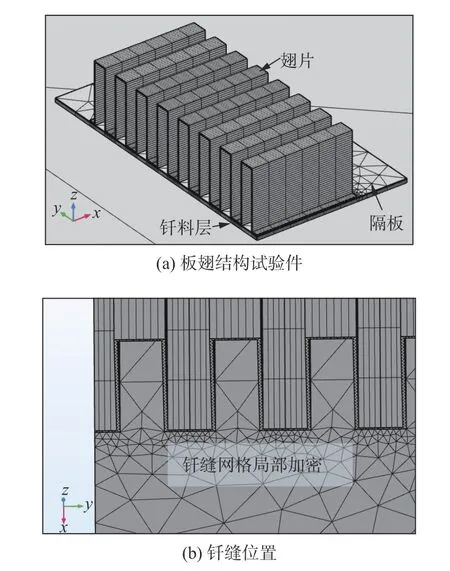
图3 板翅式换热器结构网格模型Fig.3 Mesh model of a plate-fin heat exchangers.(a)plate-fin structure test piece;(b) position of brazing seam

1.3.2 真空炉传热模型及边界条件建立

真空钎焊过程是炉体及工件内部加热、保温及快速冷却的过程，整体的温度场分布随时间产生剧烈变化.此外，材料热物理性能参数也随着温度的变化而变化，并且存在熔化和相变产生的潜热现象.因此，真空钎焊过程的温度场属于典型的非线性瞬态热传导问题.真空钎焊炉中主要发生的传热过程为加热带与工件表面间的热辐射以及工件内部的热传导，不存在工件与环境介质的对流换热，如图4所示.

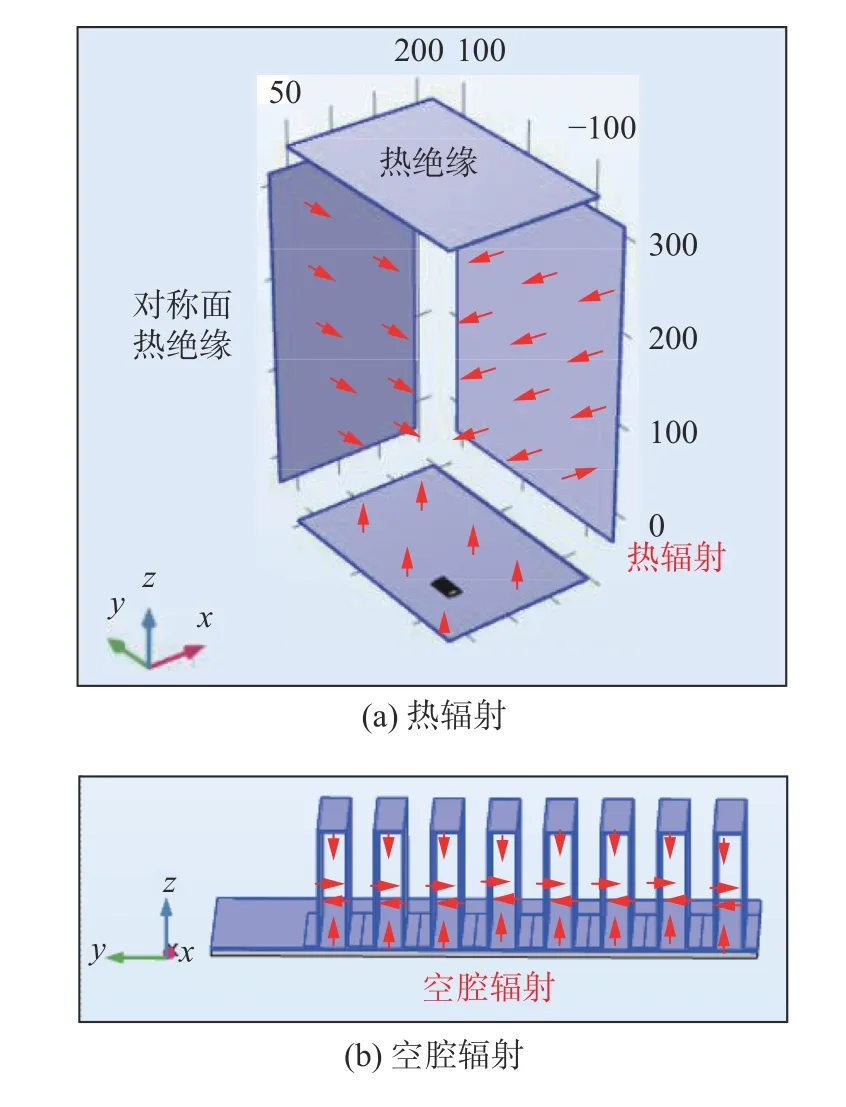
图4 真空钎焊炉中传热模型(mm)Fig.4 Heat transfer model.(a) thermal radiation;(b) cavity radiation

热传导可由式(1)描述，加热带热源功率将折算为热耗率加载至几何模型上.方程为

式中：ρ为钎焊材料密度；c为比热容；λ为导热系数；T为温度；为内热源强度；t为传热时间.其中，钎焊材料密度ρ、比热容c、导热系数λ随温度T而变化.

式(1)为泛定方程，求解需给出初始条件和边界条件.通常将边界条件分为以下3类[12-15].

已知边界上的温度为

已知边界上的热流密度分布为

已知边界与周围环境的热交换为

式中：n为边界的表面外法向量；q为材料单位面积上的热输入；α为换热系数；Tα为环境介质温度.

实际焊接过程中一般为热流与换热边界条件.然而，在该过程中炉壁功率是动态变化的，且难以获得真空炉的实时电压电流特性曲线.为了实现实际真空钎焊炉的温度实时调控功能，引入事件接口为

式中：Pw为热源功率；η为热源效率；U为真空炉电压；I为真空炉电流；O为状态系数.

当计算域温度低于设定温度时置为1，高于设定温度时置为0.通过这种方法，即便无法测得真空炉的电压电流特性曲线，也能实现近似的热源动态.将加热带外部与对称面设置为热绝缘边界.加热带与工件表面之间的热辐射传热可表示为[16]

式中：q为单位曲面面积的辐射热流；ε0为表面辐射率；σ为Stefan-Boltzmann常量；θ为温度；θ0为给定初始温度.此外，还需考虑板翅结构封闭通道内的空腔辐射，即但只考虑曲面自身的热吸收或热释放，而且考虑了有限空间内曲面之间的热反射，是曲面间的辐射热交互作用，可表示为[17]

式中：q为单位曲面面积的辐射热流；εi为表面辐射率；σ为Stefan-Boltzmann常量；θi为温度；F为曲面视角因数；C为曲面反射矩阵；其中F与两曲面的距离和法线方向有关.

传热分析得到的温度变化被作为热载荷导入到结构分析中，由夹具施加的压力均匀分布在结构的上表面，由结构的热弹塑性响应，则可得到结构残余应力分布及热变形.其求解过程为：首先把构件划分成有限个单元，然后逐步加上温度增量.每次温度增量加载后，由Kdδ=dF可求得各节点的唯一增量dδ. 每个单元内的应变增量dε和单元位移增量dδ的关系为

式中：B为联系单元中应变与节点位移向量的矩阵；单位向量ε 为应变增量；单位向量δ 为位移增量.

再根据式(10)的应力应变关系可求得各单元的应力增量dσ.这样可以了解整个焊接过程动态应力应变的变化过程和最终的残余应力和变形状态.应力应变关系为

式中：D为弹性矩阵；单位向量ε 为应变增量；C为曲面反射矩阵；T为温度向量.

1.3.3 材料热物性参数

在钛合金板翅结构真空钎焊过程的热-固耦合仿真计算中，为保证计算结果的准确性，必须采用与所用材料属性相同的热物理性能参数.仿真所用TA1钛合金、Ti-Zr-Cu-Ni钎料主要热物理性能参数如表2所示.真空钎焊炉炉壁加热带的主要热物理性能参数如表3所示.此外为提高计算的准确性，针对钛合金和钎料的热导率及热容，建立了其与温度的曲线关系并加载到模型中.

表2 TA1钛合金、Ti-Zr-Cu-Ni钎料物理参数Table 2 Physical properties parameters of TA1 titanium alloy,Ti-Zr-Cu-Ni filler metal

表3 炉壁主要热物理性能参数Table 3 Main thermophysical properties parameters of furnace wall

1.3.4 温度场校核

为验证所建模型的准确性，该文对比了仿真与试验的节点热循环曲线，模型验证如图5所示.可见，两者的数值相近且变化趋势一致.因此该文建立的热-固耦合模型可获得较准确的温度场计算结果.

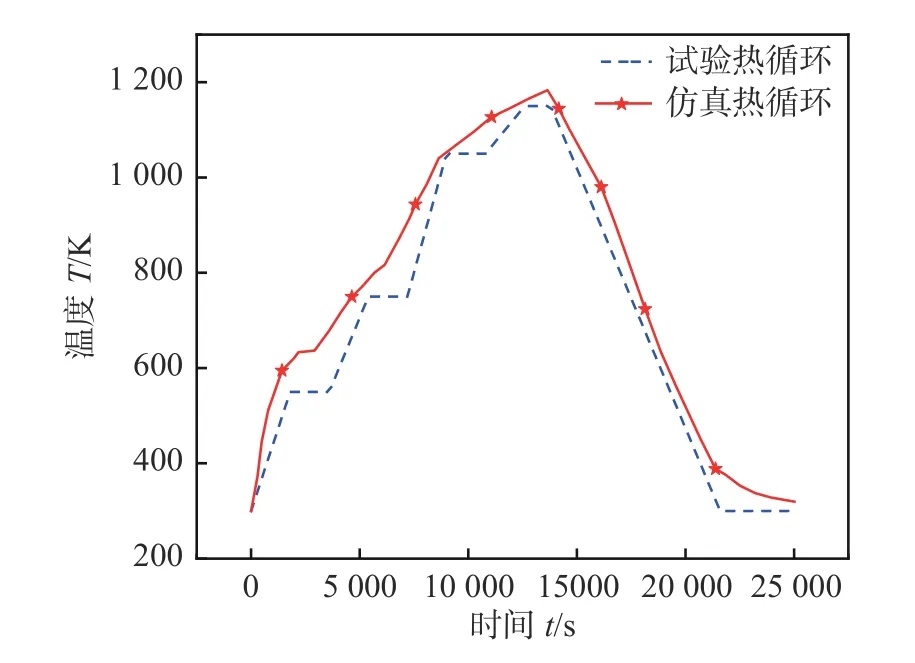
图5 热-固耦合模型验证结果Fig.5 Verification results of thermal-solid coupling model

2 仿真结果

2.1 钎焊时间对钎焊过程温度场的影响

该文设计了如图6所示的4种真空钎焊工艺曲线，分别为：1号工艺保温时间20 min；2号工艺保温时间10 min；3号工艺保温时间30 min；4号工艺各阶段保温时间由10 min到30 min逐渐增大.4种工艺均为4次升温分别记为S1，S2，S3，S4，平均升温速率7.1 K/min.通过对比各工艺间的温度场分布，即可明确保温时间对工件温度均匀性的影响规律，从而为优化钎焊工艺提供理论依据.不同保温时间下的钛合金板翅结构真空钎焊温度场分布结果如图7所示.对比1号工艺各时刻下温度场分布可见，各时刻下温度场对称分布均为两侧温度较高，中部温度较低.保温可显著促进工件的温度均匀性.真空钎焊热传导主要发生在翅片、钎料、隔板以及夹持工装间.翅片结构上下表面、钎料及隔板并没有受到加热带的直接辐射加热，而是通过夹持工装的热传导进行加热，因此传热效率与接触面积及材料本身的导热性有关.对于工件的内部翅片，除了受到热传导的作用外，还受到内部翅片表面的辐射与反射，这种热效应将随着温差的减小而不断递减，因此越靠内的翅片受热将越微弱，表现为工件两侧温度较高，中部温度较低.纵向对比1号、2号和3号工艺下的温度场分布可知：保温时间的长短对温度峰值影响不显著，仅改变工件的温度均匀性.保温时间越长，板翅结构表面的低温区范围越小，表明工件的温度分布越均匀.足够的保温时间可保证工件中部受到热传导与空腔辐射的充分加热，工件的最大温差因此减小，温度分布更均匀.此外，还可发现在S1～S2低温阶段10～20 min的保温时间即可获得较均匀的温度分布，而该阶段的温度均匀性仅影响板翅结构的热变形，不影响钎料的熔化与凝固.因此可在低温阶段采用较短的保温时间，而在S3～S4高温阶段适当延长保温时间，从而在获得较好温度均匀性的同时缩短工艺时间，如图7的4号工艺所示.

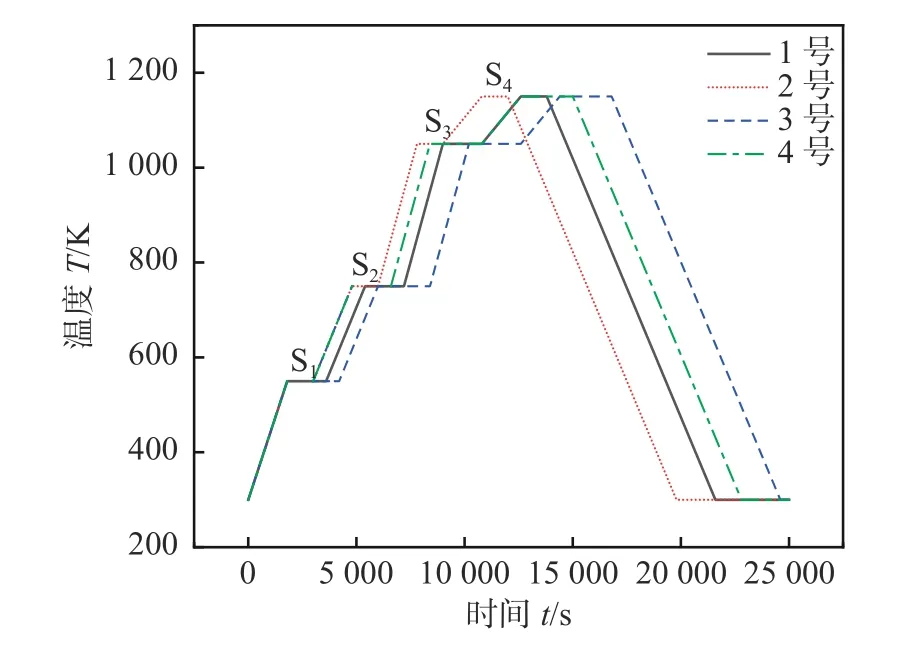
图6 不同保温时间的工艺温度曲线Fig.6 Process temperature profiles for different holding times

图7 不同保温时间下的钛合金板翅结构真空钎焊温度场分布Fig.7 Temperature field distribution for vacuum brazing of plate-fin heat structures at different holding times

2.2 时间对钎焊过程残余应力的影响

为探究保温时间对钛合金板翅结构钎焊残余应力的影响，分别采用20 min，25 min，30 min和35 min的保温时间进行仿真研究.不同保温时间下，钎焊残余应力分布的对比结果如图8所示.对比1号工艺各时刻下残余应力分布可知，残余应力分布具有明显的对称性，隔板下表面中间位置的残余应力最大，残余应力峰值为357 MPa；钎缝处同样存在应力集中，残余应力值为142 MPa.板翅结构表面残余应力主要集中于翅片上表面与隔板背侧中部.其中，翅片上表面的应力呈现明显的两端大中间小的分布特征，由板翅结构变形的分布特征可知，这是由于x方向上两侧的挠曲变形略大于中间，使得装夹工装的夹持压力主要作用在翅片上表面的两端，而中间受压较小.板翅结构背侧的残余应力主要集中于中部，这是由于隔板在y方向上的变形远大于x方向上的变形，因此板翅结构背侧的主要受压位置为隔板中部，而两侧的受压相对较小，可以通过自由变形释放残余应力.不同保温时间下板翅结构的残余应力分布无显著变化，残余应力均主要集中于翅片上表面与隔板背侧中部.在冷却过程中，板翅结构的钎焊热应力主要通过变形释放.因此保温时间越长，板翅结构的整体变形越大，残余应力越小.

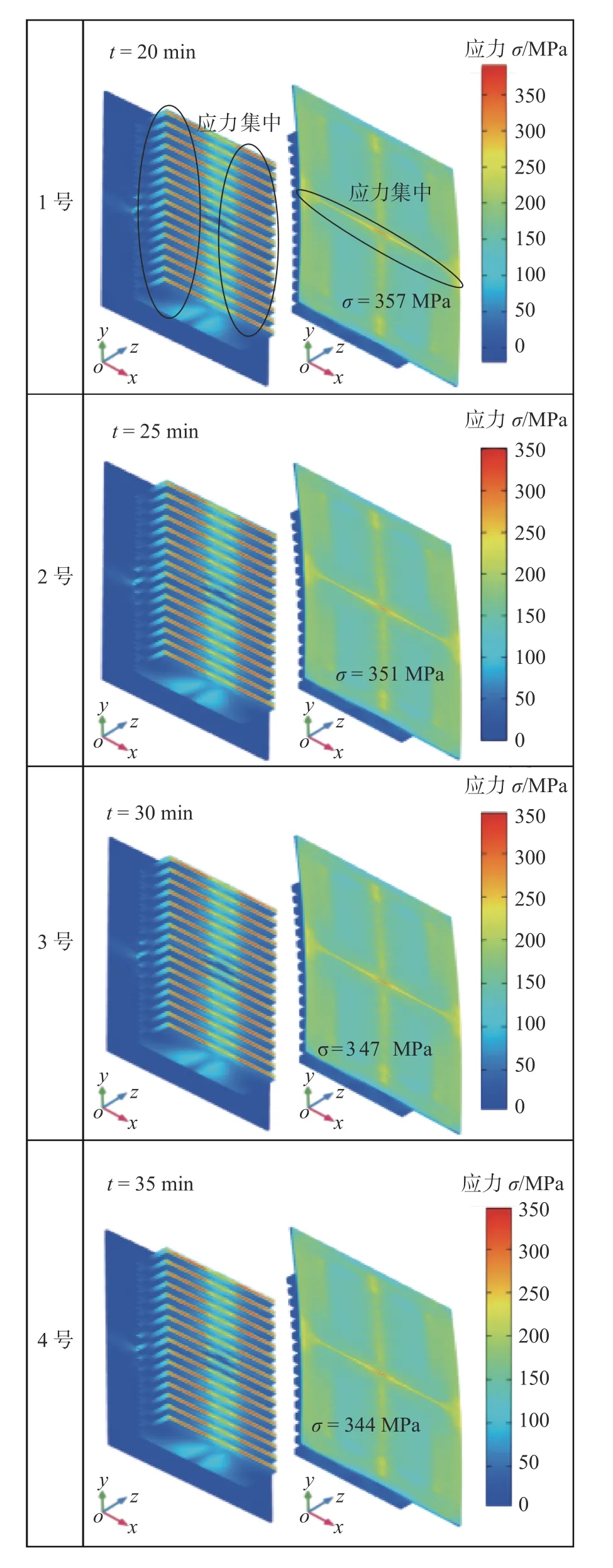
图8 不同保温时间下的钛合金板翅结构真空钎焊残余应力分布Fig.8 Residual stress distribution for vacuum brazing of titanium alloy plate-fin structures at different holding times

不同保温时间下翅片残余应力分布的对比结果如图9所示.结果表明，不同保温时间下翅片残余应力分布无显著变化，残余应力均集中于翅片钎缝的角点处.当t=20 min时，各个翅片的钎缝角点残余应力峰值为142 MPa；当t=25 min时，各个翅片的钎缝角点残余应力峰值为139 MPa；当t=30 min时，各个翅片的钎缝角点残余应力峰值为138 MPa；当t=35 min时，各个翅片的钎缝角点残余应力峰值为137 MPa.可见，保温时间越长翅片钎缝的残余应力越小.

图9 不同保温时间下的钛合金板翅结构真空钎焊局部残余应力分布Fig.9 Local residual stress distribution for vacuum brazing of titanium alloy plate-fin structures at different holding times.(a) 20 min;(b) 25 min;(c)30 min;(d) 35 min

2.3 残余应力结果对比校核

为校核所建钛合金板翅式换热器热-流-固耦合模型的准确性，采用X射线衍射法对板翅结构试验件进行无损残余应力测试.由于板翅结构翅片间隙小于X射线探头直径，无法对试验件正面的残余应力进行测试，因此选取的残余应力测试点位如图10所示.

图10 X射线衍射残余应力测试点位置Fig.10 The location of the X-ray diffraction residual stress test points

测试P1，P2每个测试点的横向与纵向两个方向的残余应力，分别采用σx和σy表示.残余应力测试结果如表4所示.由表4可知P1，P2两点的残余应力数值相近，主要为200 MPa左右的y向压应力.

表4 残余应力测试结果Table 4 Results of residual stress tests MPa

图11为热-固耦合模型计算得到板翅结构下表面残余应力云图，对应P1点残余应力值为241 MPa，P2点残余应力值为256 MPa.对比分析热-固耦合模型计算得到的应力分布与试验结果发现，温度场-应力场耦合模型计算值与试验值偏差为5.3%.

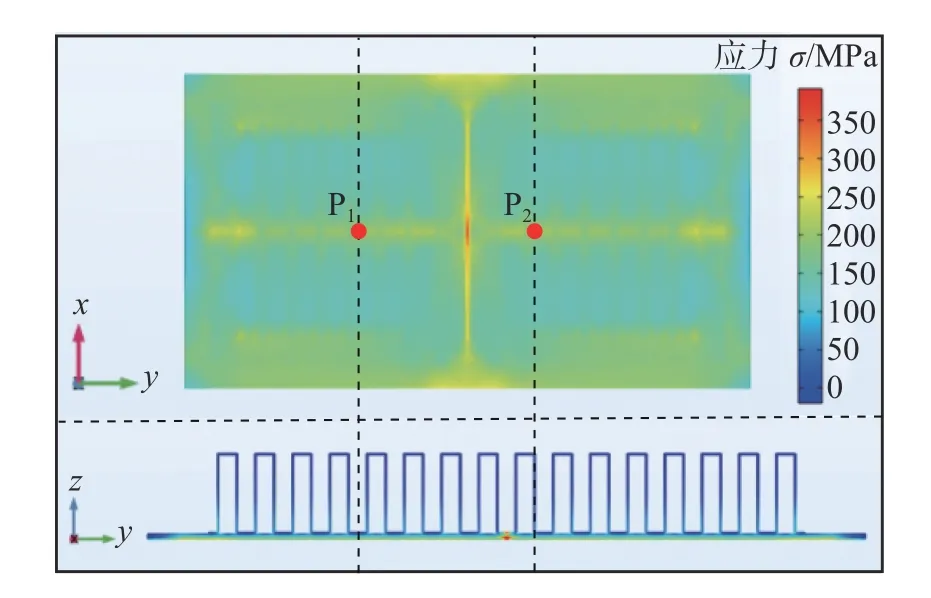
图11 板翅结构下表面残余应力分布Fig.11 Residual stress distribution on the lower surface of plate-fin structure

3 结论

(1)建立了钛合金板翅式换热器真空钎焊过程热-固耦合模型，残余应力仿真结果与试验值的偏差为5.3%.

(2)延长保温时间可有效改善板翅结构的温度均匀性.在制定真空钎焊工艺时，可适当降低升温速率并延长保温时间.

(3)板翅结构钎焊后在钎缝及夹持点处存在明显的应力集中现象，且随着保温时间的减小而减小.