基于圆孔标定板的视觉机器人手眼标定方法

邓惠铭,潘知康,林行威,张烈山

(浙江理工大学,浙江 杭州 310018)

0 引言

机器人视觉系统作为智能机器人的重要组成部分,可以协助机器人完成工厂的各类生产、加工任务[1-2]。在工程测量领域,具有抗干扰能力强、精度高等优点的线激光传感器已经广泛应用[3]。受测量范围限制,线激光传感器只能测量得到物体的局部表面数据。然而,将线激光传感器加装到灵活的机器人上后,通过机器人带动线激光传感器移动,便可以对物体进行完整测量,进而提升机器人系统的柔性[4]。

将线激光传感器加装到机器人上后,需要确定好机器人法兰盘坐标系与线激光传感器坐标系之间的位姿转换关系,求解这一转换关系的过程被称之为手眼标定[5]。目前,最普遍的手眼标定方法是借助特定的标定物,将标定物放在空间中的固定位置,通过控制机械臂使视觉传感器与标定物之间发生相对运动,视觉传感器获得标定物的外形测量数据,再结合机械臂的运动数据建立标定模型,求解之后就可以得到视觉传感器坐标系与机器臂的基坐标系之间的转换关系矩阵,这个转换矩阵就是手眼标定矩阵。曹冬旺等[6]以标定球作为标定物,利用标定球球心在基坐标系中坐标不变的原则,完成手眼标定。杨守瑞等[7]使用标准球作为标定参考物,建立了手眼标定模型并结合了机器人运动学参数误差,获得了不错手眼标定精度。然而球形标定物加工难度大,加工成本高,且每次测量都要对截面进行拟合,增加了求取球心坐标的误差。高金锋等[8]以圆柱作为标定物,通过改变机器人的姿态对圆柱侧面扫描。以圆柱中轴线为约束建立优化方程,利用智能算法求解优化,得到手眼标定的变换矩阵。孙炜等[9]使用阶梯型标定物,将线激光传感器对准标定物的标记点,利用最小二乘法求解手眼标定矩阵。He 等[10]提出一种使用任意曲面作为标定物的标定方法,该方法可以对机器人的几何参数与手眼标定参数都进行补偿。Yu 等[11]提出了一种在线检测手眼标定误差的方法,系统可以自动补偿机器人运动学参数和手眼标定误差。Hu等[12]使用线激光传感器配合摄像机联合标定的方法,不需要制作标定物,但该方法需要满足每条激光条纹之间成非线性关系,操作过程比较烦琐。虽然学者们已经对手眼标定的方法进行了大量的研究,但这些方法要么数学模型和操作过程极为复杂,难以适应复杂的工业现场环境;要么标定精度不足,限制了整个机器人系统的性能。因而找到一种简单、快捷、适应性强的标定方法是有必要的。

本文针对搭载线激光传感器的六自由度机器人系统,提出了一种圆孔标定板的手眼标定方案。该方案通过改变机器人的位姿,使得线激光传感器扫描到圆孔标定板的圆心点,将其圆心点视作空间中的固定点。结合机器人的运动学参数,建立起系统模型,使用最小二乘法辨识出机器人的手眼标定矩阵。为了验证该方案的优势,分别对传统的标准球方法与本文方法进行仿真和实验,以标定后的机器人系统带动扫描仪对精加工平面扫描,将实测到的点云与最小二乘法拟合平面之间距离的均方根作为评价的标准[13]。本文方法的圆孔标定板具有易加工、标定步骤简单、精度高和抗干扰能力强的特点,可以满足工业中的复杂环境。

1 机器人手眼标定模型

针对机器人末端使用线激光传感器的机器人手眼标定问题,本文提出了一种基于圆孔标定板的手眼标定方案。如图1所示,该方案的模型主要是由工业机器人、线激光传感器和圆孔标定板组成。

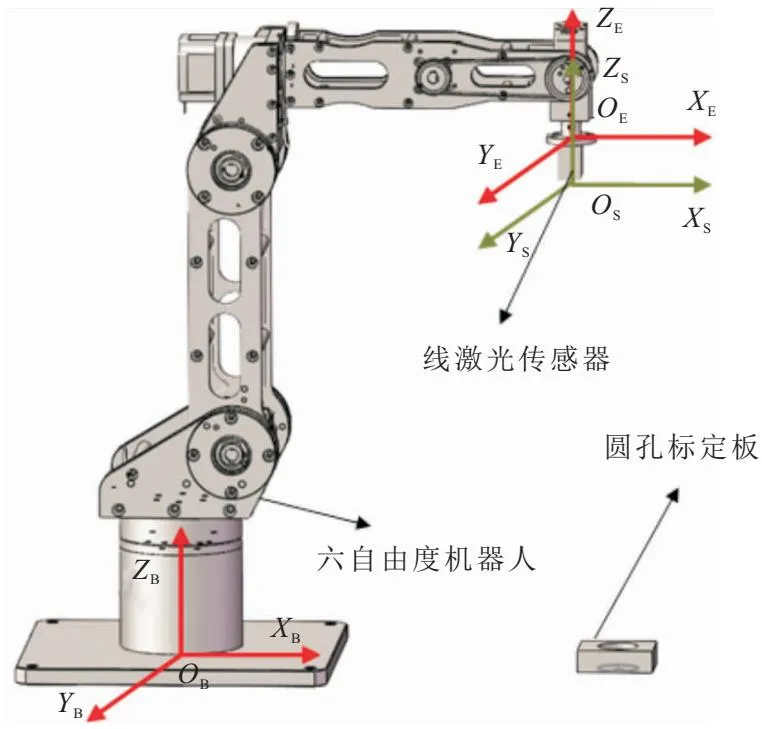
图1 手眼标定模型

线激光传感器装载在机器臂的末端法兰盘上,通过多次改变机器臂姿态来使线激光传感器对圆孔标定板圆心点扫描,可以得到圆心点在线激光传感器坐标系OS-XSYSZS下的位置XS和在机器人基坐标系OB-XBYBZB下的位置XB。两者之间的转换公式为

(1)

传统的机器人手眼标定方法使用的是标准球,而使用标准球标定的方法需要对每次扫描生成的球截面上的点坐标进行圆拟合,从而求解扫描截面圆心的坐标,这样会加大求解球心坐标的误差。而本文所使用的圆孔标定板,可以通过线激光传感器直接得出圆心点的坐标,由于圆心点坐标是由线激光轮廓扫描仪直接扫描得到的,所以每次测量时,空间中圆心点三维坐标中的其中一维可以置零。相比于传统的标准球测量方法,本文方法不仅减少了拟合圆的步骤,且减少求解圆心坐标的步骤,规避了这一步产生的误差,从而提升标定精度。

2 手眼关系标定原理

分别用传统标准球方法与本文方法进行比较,并对标定流程进行介绍。

2.1 标定过程数据采集方法

传统方法对照组实验使用直径20 mm的球形标定物,采集方法如下所述。

控制机器臂变换姿态带动线激光传感器对标准球的球面进行多次扫描,并把扫描得到的点云数据进行预处理,把无效数据去除后保留截面圆的点云数据。对点云数据进行圆拟合,得出截面圆的圆心坐标(xS,zS)和截面圆半径r,并把机器人6个轴的姿态数据传输到计算机上。记录截面圆与球心的位置关系,人工判定球心在线激光传感器坐标系中y轴的符号正负,根据式(2)得出球心点坐标(xc,yc,zc)。由于y轴坐标值的正负依赖于人工判断,当坐标值较小时很容易产生误判,从而造成标定误差。

(2)

使用本文采用的标定板进行标定时,采集方法如下所述。

如图2所示,每次扫描都控制机械臂使得线激光扫描仪的蓝光线对准圆孔的圆心标记点。获取数据后再对点云数据进行预处理。如图3所示,对截面二维点云数据进行数据处理,寻找到圆孔的左右边缘点(x1,z1),(x2,z2)。对扫描到的标定物平台面点云数据进行直线拟合,即

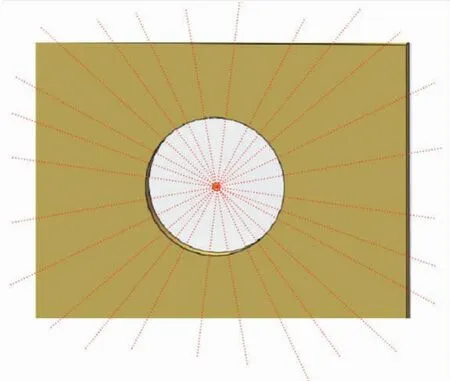
图2 圆孔标准块的扫描位置

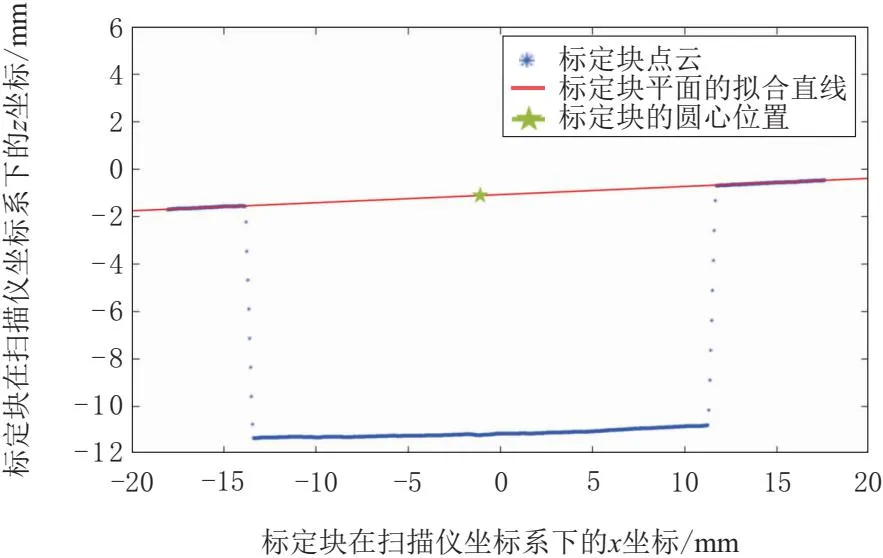
图3 圆孔标定板圆心点

z=kx+b

(3)

由于圆心点在拟合的直线上。根据式(4)可得出在线激光传感器坐标系下圆心点坐标为(xd,0,zd)。

(4)

2.2 手眼标定初值计算

通过上述采集步骤得到空间中标准球的球心坐标和圆孔标定物的圆心坐标。多次扫描后即可获得在线激光传感器坐标系OS-XSYSZS下的坐标点集{P=Xi|i=1,2,3,…,n},由于圆孔标定板在空间中是固定的,所以圆心点在基坐标系OB-XBYBZB下的坐标是不变的。可得到

(5)

在得到式(5)方程组后,可推得下列关系,即

(6)

式(6)可以改写为

(7)

i=1,2,…,n

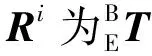
式(7)中左式减去右式,化简可得

(8)

这样就获得了型如Ax=b的方程组。最小二乘法的求解公式为

x=(ATA)-1ATb

(9)

求解出r1、r3和t后,根据坐标系右手定则,可以得出

r2=r1×r3

(10)

通过式(6)～式(9)可以求出手眼关系的矩阵。但这个结果没有将机器人的运动学误差纳入考虑范围,标定结果误差较大。在本文标定方法中,将把这个手眼标定结果当作初始值,再加入机器人运动学参数误差,对手眼标定结果进行优化。

2.3 运动学误差辨识

机器人误差是指机器人末端法兰盘的实际位姿与理论位姿之间的偏差。由于机器人运行过程中发热导致温度变化以及机器磨损等原因,会导致机器人末端的轨迹与理想的轨迹有偏差,因此在本文研究中,将建立机器人误差模型,辨识出机器人运动学参数误差并进行补偿优化。

本文采用的机器人建模方法为改进后的MDH建模[14]方法,模型如图4所示。

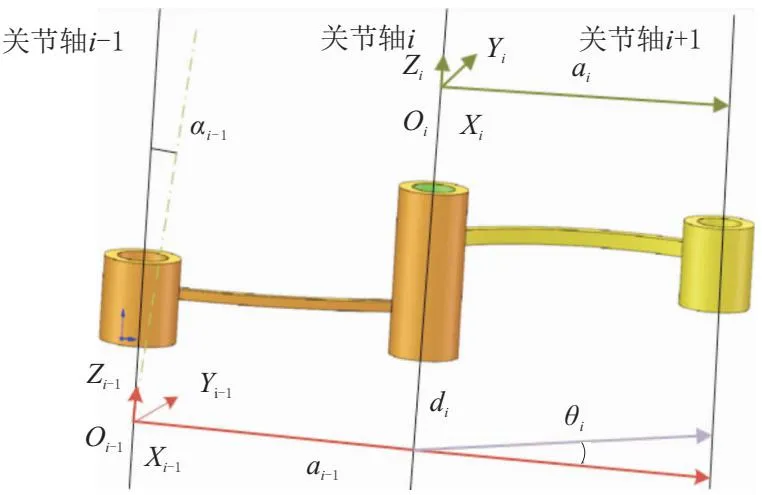
图4 机器人MDH模型

相邻关节的齐次变换通式为:

Rot(z,θi)Trans(z,di-1)Rot(y,βi)

(11)

式中:Trans( )为平移变换;Rot( )为旋转变换;c为cos简写;s为sin简写;i=1,2,…,6为关节序号;αi-1、θi、βi分别为绕关节轴i-1的x轴、y轴和z轴正向(右手准则确定)旋转的度数;ai-1和di分别为沿着关节轴i-1的x轴和z轴正方向的位移。

如图4所示,关节坐标系{Oi-1}的x轴为关节i-1轴公垂线指向关节轴i的公垂线,z轴和关节轴i-1共线,方向与i-1轴正方向相同。y轴由确定好的x轴和z轴确定。

系统误差模型为

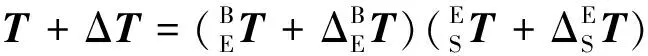
(12)

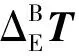
(13)

根据机器人微分运动学原理,有:

ΔT=TδT

(14)

(15)

可得

(16)

结合式(11)～式(16)把误差辨识的公式写为

Ax=b

(17)

式中:A为3×36的误差系数矩阵,包括30个机器人运动学参数和6个手眼关系矩阵参数;b为末端实际位置与理论位置之间的差值;未知量x为参数误差Δq,Δq参数[15]又主要包括独立参数、相关性参数和不起作用的参数3种类型。

在求解的过程中,相关性参数和不起作用的参数会对求解过程造成影响,导致对Δq的求解精度降低。而去除这些参数又不会对误差结果产生影响,所以辨识之前要将这些冗余参数去除。由于已有学者已总结好冗余参数辨识的准则,本文将不再赘述。

在本实验平台中,机器人雅可比矩阵中30个参数中共冗余15个MDH参数。如表1所示。

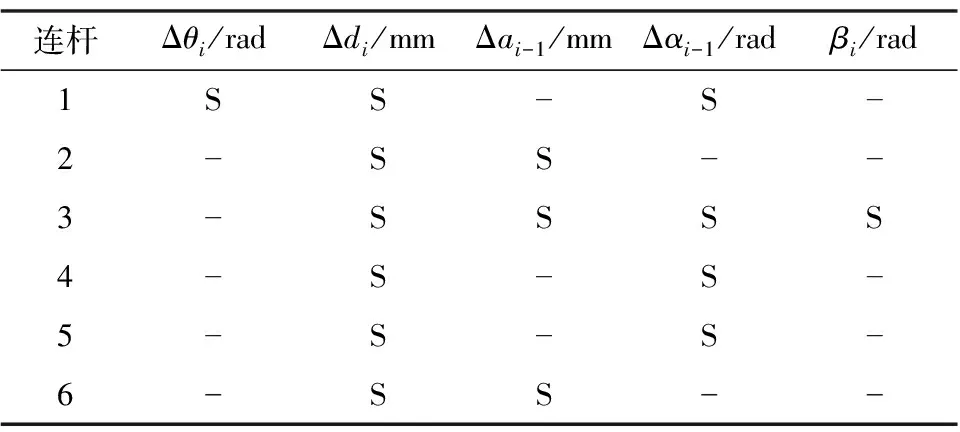
表1 Z3-R650机器人可辨识参数表

表1中,“S”表示保留的MDH参数,“-”表示冗余的MDH参数,需要去除。因此在辨识误差时只需要对这15个MDH参数和手眼矩阵的6个参数进行误差补偿。

通过最小二乘法对式(17)求解可以得到辨识的参数误差Δq,再设定误差上限,使加入补偿后的机器人MDH参数不断迭代,直到收敛至预想的标定结果。算法的总体流程如图5所示。

图5 标定算法流程

经过实验测试,将Δq、Δα、Δβ的阈值设为1×10-12rad,将Δd、Δa的阈值设为1×10-12mm时,标定精度较好,因此本文将该值设置为此。

3 数值仿真与实验

3.1 数值仿真分析

分别建立传统标准球方法与本文圆孔标定法的数学模型,本文将对2种方法进行仿真分析对比。手眼标定结果的误差主要来源包括线激光传感器扫描坐标的误差和机器人的绝对定位精度误差。本文所使用的线激光传感器的最大误差为±0.02 mm。机器人变换姿态后末端位置和姿态出现的误差符合高斯分布N(0,σ2)。为了验证本文方法和传统标准球方法对误差的抗干扰性能,人为给扫描仪点云数据添加0～0.5 mm的微小扰动,给机器人MDH参数模型中除去冗余参数后的3个连杆转角参数α、1个关节角参数θ和第3个关节轴的附加转动项参数β3添加0.1 rad的角度误差,给6个连杆偏距参数d和4个连杆长度参数a添加0.1 mm位置误差。设定相同的手眼变换矩阵,分别建立结合机器人MDH参数模型的误差模型,从而获得2种标定方法受到误差影响的手眼变换矩阵和MDH参数的补偿结果。为保证仿真结果的随机性和普遍性,本文进行了100次仿真实验,结果如表2、图6～图9所示。

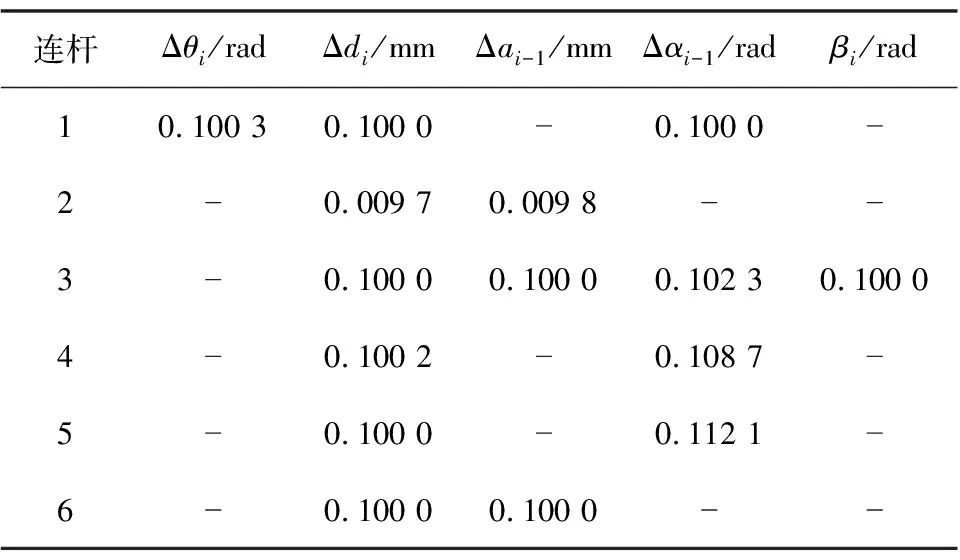
表2 辨识出的MDH参数误差

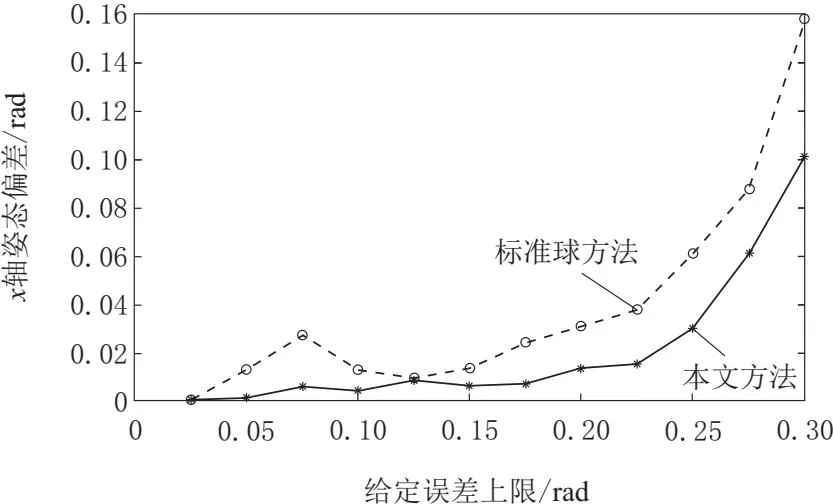
图6 手眼矩阵x轴的姿态误差

图7 手眼矩阵y轴的姿态偏差

如表2所示,给机器人参数增加固定的微小扰动后,本文的算法都可以将其辨识出来。“-”为去除掉的冗余参数,因此不需要补偿。由图6～图8可知,使用本文的方法手眼标定时,相对于传统标准球方法,当给点云数据加上随机误差上限在0～0.2 mm之间时,两者之间差别不大。在误差上限增大到0.2 mm以上的时候,姿态矩阵的x、y、z轴的抗干扰能力都有提升。特别地,由于本文的标定方法使用的原始点云的y轴坐标都为0,因此,使用本文方法标定的手眼矩阵的y轴姿态要比传统标准球方法抗干扰性更好。如图9所示,使用本文的手眼标定方法在位置误差上也要明显优于传统的标准球方法,有效地提高标定的抗干扰性能和标定精度。

3.2 手眼标定实验

本文搭建的实验平台如图10所示,主要由阿姆洋Z3-R650六自由度机器人(重复定位精度为0.05 mm)、基恩士L-JV7000线激光轮廓扫描仪(传感器精度为0.02 mm)以及上位机组成。本文将使用该平台分别圆孔标定板与传统的球形标定物进行对比实验。

图10 搭建的实验平台

2种方法使用同样的手眼位置关系,分别对2种标定板采集点云数据,并计算出MDH参数误差补偿值和空间约束点在基坐标系下的位置标准差,如表3、图11和图12所示。

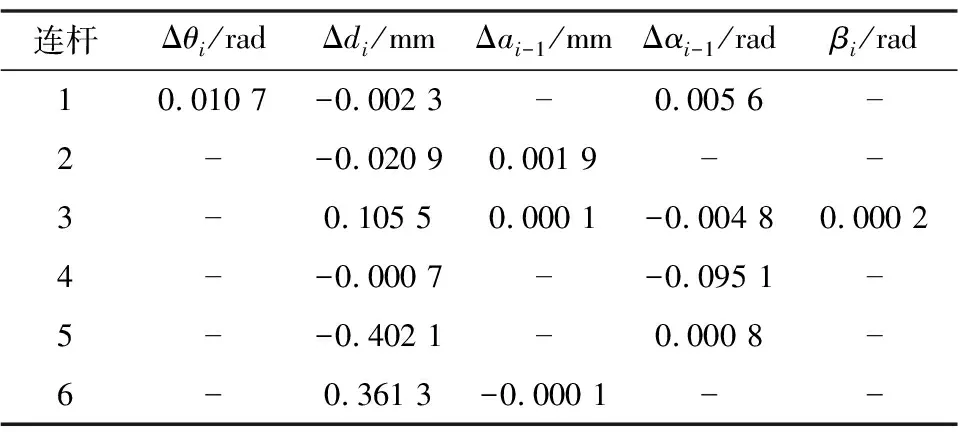
表3 实验平台辨识出的MDH参数补偿

图11 实验组数与位置误差关系

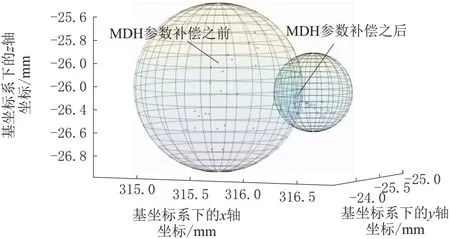
图12 MDH参数补偿前后的效果对比

表3为本文搭建的实验平台所辨识出的15个MDH参数补偿值,“-”为冗余的参数,不需要补偿。图11为线激光传感器坐标系下的球心点坐标反求回基坐标系下后的位置标准差。与传统的标准球法相比,在相同的实验平台条件下,传统标准球方法需要控制机器臂扫描40组数据以上后手眼关系矩阵比较稳定,位置标准差控制在0.16 mm以内。而使用本文圆孔标定法在MDH参数补偿前后都是需要30组数据后手眼关系矩阵就可到达稳定状态,位置标准差稳定在0.10 mm以内。图12为圆孔标定法在补偿MDH参数前后在基坐标系下的位置对比。从图中可以明显看到,在参数补偿之后,反求回去的圆心位置在基坐标系下更加收敛,稳定性更好。

为了验证本文手眼标定算法的准确性和精度,本文将采用参考平面度误差[16]的评价方法对标准球方法与圆孔标定法进行对比。由于本文所使用的精加工平面的平面度误差0.01 mm,相对于手眼标定的误差可以忽略不计。因此若手眼关系矩阵没有误差,扫描出来的点云在基坐标系下将为均方根为0的平面。实际上由于手眼标定的结果存在误差,基坐标系下的点云将偏离实际点云平面,这样扫描出来的点云与拟合平面之间就会产生类似于平面度的误差。因此,这个误差可以反映手眼关系矩阵的精度。通过改变机器人姿态,使线激光扫描仪对精加工平面进行扫描进而获取平面的点云。精加工平面图机器扫描后的效果如图13～图16所示。

图13 精加工平面

图13为精加工平面现场实拍。如图14所示,得到实际点云位置信息后,再进行平面拟合,进而求出点云与拟合平面的均方根误差来评估精度。通过多次变换精加工平面空间中的位置,求取各位置点云与拟合平面的均方根误差。本文随机摆放了10个精加工平面位置,计算出对应的点云与拟合平面的均方根误差。

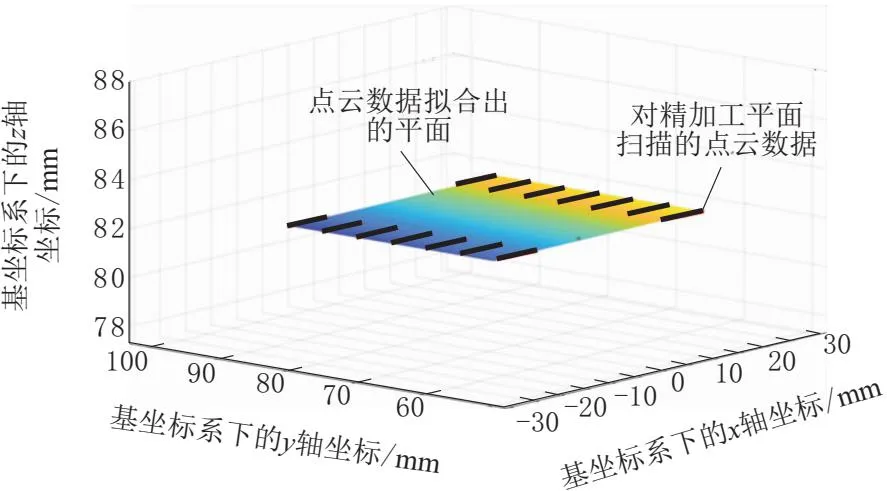
图14 实际点云与拟合平面

图15为其中1个位置处所有点云与其拟合平面之间的距离。图16为10个位置处的均方根误差。由图15和图16可知,使用圆孔标定板方法的均方根误差与标准球方法相比从0.212 mm下降到0.121 mm,引入MDH参数补偿后下降到0.065 mm,减少了实际点云到理想平面之间的误差。说明在同样的实验平台下,本文方法比标准球方法的精度更高,实验结果与仿真结果一致。

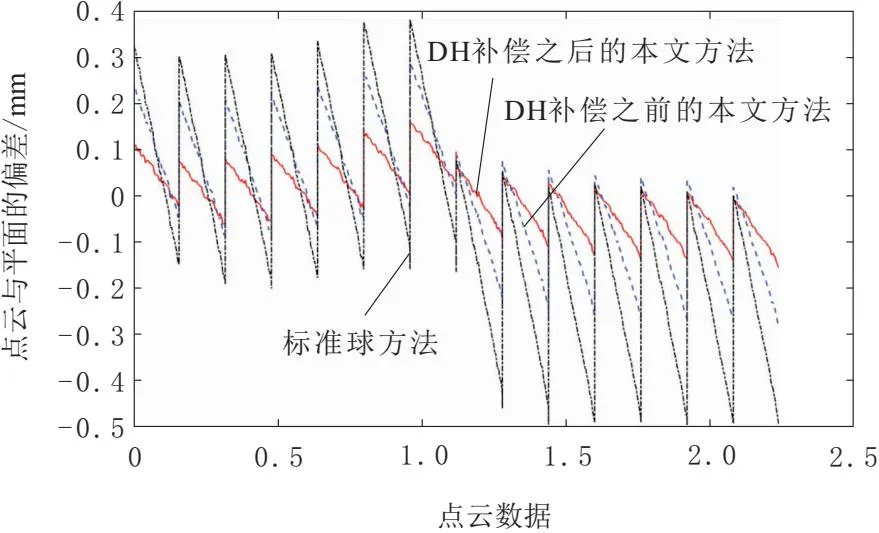
图15 位置1处点云与拟合平面距离

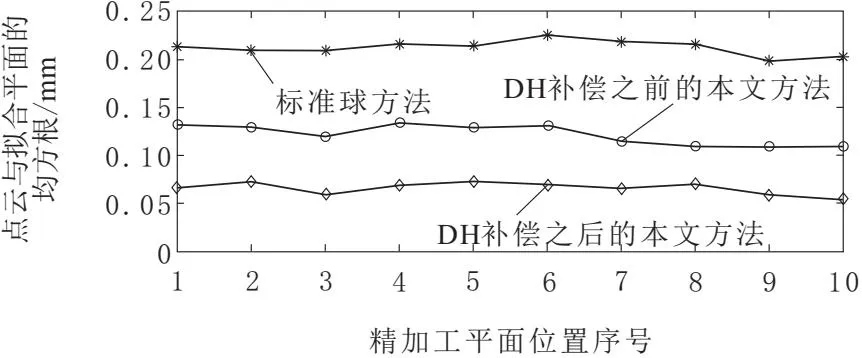
图16 点云与拟合平面均方根误差

4 结束语

本文针对装备线激光传感器的智能机器人系统手眼标定问题,提出了一种基于圆孔标定板的手眼标定方法应用。将圆孔标定板圆心作为空间中固定点,建立包含机器人MDH参数误差辨识的手眼标定模型,并使用最小二乘法不断迭代更新MDH参数误差模型与手眼关系矩阵,直至达到理想值。

此外,本文将传统标准球方法与圆孔标定板方法进行仿真与实验对比。在仿真实验中,在给定MDH参数误差后,本文的算法可以将其辨识出来。对扫描出来的点云数据添加相同上限的随机误差后,本文方法比传统标准球方法的标定结果精度更高,稳定性更好。同时,本文采用平面度误差的评价方法,通过对平面度误差为0.01 mm的精加工平面扫描得到点云数据,将其反求回基坐标系后,MDH参数补偿后的本文方法与标准球方法相比,均方根误差由0.212 mm下降到0.065 mm。实验结果与仿真预期结果一致,验证了本文方法的可行性和实用性。