基于非线性规划的风光储配置策略

河北工业大学 张雅伦

1 问题描述

本文以风光储配置的总价更少，电网每个小时发出的电量变化波动更小为目标建立了多目标规划模型，给出了特定数值下的最优配置方案。在以上问题的容量配置基础上，考虑到不同时段电价不同，通过储能装置的调节来得到风光储能电网的最佳运行出力。以一天时间为周期建立多目标规划模型，在与问题相似的约束条件下求解。下文是具体问题：为配电网的1～15个节点合理地配置风光储使得配置总价更少的同时，使电网每小时发出电量变化波动也最小；在第一容量配置不变的基础上，以经济性和低碳性为目标，优化风光储的配置。

2 模型假设

一是忽略电能传输时的损耗，主要是高压电缆阻抗导致的；二是涉及的电路器件如变压器等均为理想器件；三是风光储设备产生的能量能供应到电网的其他负载，能量通过负载节点间的网络传递。

3 符号说明

Si,t表示t 时刻编号为i 的电缆上电能的功率，Vi,t表示t 时刻第i 个储能设备剩余的电能，Pi,t表示t 时刻第i 个储能设备的功率，ai,t表示第i 个风发电设备t 时刻的功率，bi,t表示第i 个光发电设备t 时刻的功率，ui表示编号为i 的电缆的最大流量，wi,t表示t 时刻第i 个负载的额定功率，ci表示第i个储能设备的最大容量。

4 问题一模型的建立与求解

4.1 模型的建立

问题一考察风光储设施在网络上的建立与配置。题目中电网上有16个负载，如图1所示。

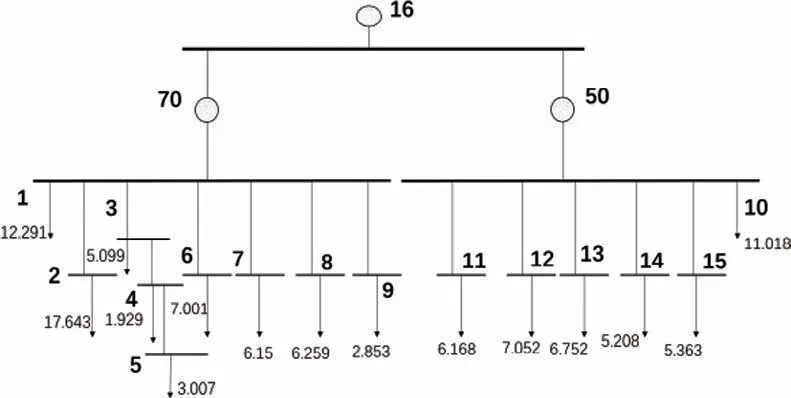
图1 电网系统示意图

由图1可知，负载的连接方式有两种。一是直接连接在供电枢纽：负载1、负载10；二是连接在其他负载上。本文将负载看作图的节点，将负载间连接的电网视为图的边，整个系统形成了一个树的结构，如图2所示。考虑到现实中电网系统的复杂性，边不仅仅是单一的导线，而是复杂电网系统的抽象，因此电流可以在边上双向传播[1]。

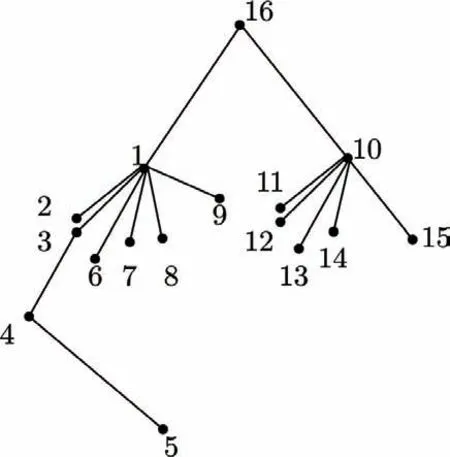
图2 电网的树状结构

风力发电、光伏发电、储能池、大电网均能对负载供电，也就是说三种设施可以配置在节点上，对节点供电。本文假设储能初始能量为0。此外，在某个节点建设的发电或储电设备也可以通过电网系统对其他结点供电。由于负载1、负载10经过变压器直接连接在大电网上，在整个系统中承担电流枢纽的功能，本文认为风光储设施不宜建立在负载1、负载10。同时，节点16直接连接大电网，此处的系统连接情况较为复杂，也不适合再配置其他设施，故不考虑在节点负载1、负载10、负载16处建立设施[2]。

节点处电路连接十分复杂，既要考虑电网、风光储的供电，还要考虑电网随时间的波动，很难建立约束方程。对此，本文不考虑节点处的能量变化，而改为考查边上不同时刻流动的能量。事实上，任一节点当前时刻的供电状况可以用和其相邻的一条或两条边的流量和自身发电量表示。

本文将每一时刻电缆上的电流的流量看作决策变量，对图上存在的边重新编号，整体采用自左向右的编号原则。得到了电网系统图如图3所示。

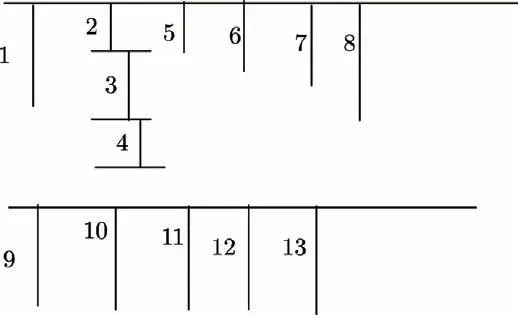
图3 对关键节点重新编号

忽视温度变化，太阳能光伏发电受太阳能辐射值影响，输出功率为：

其中：A 为光照辐射值，As 为标准状况下的辐射值，Prated为额定功率。光能发电在夜晚时不会产生电量，而在正午时产生电量最高。风力发电设备功率主要与风速有关，不稳定因素较多。储能设备可以视为一个简单的理想电容器，充放电过程没有任何的损耗，满足：

其中：C（t）为t 时刻储能设备中的能量。

在实际情况中，不同设备参数不同，不同天气情况对风光储的影响也不同。采用蒙特卡洛模拟，可以给出一天中风光设备的供电变化情况，以此为基础讨论。

对于第i（i ≠2,3）条边来说，要实现电力配置平衡需要有：

对于第2、3条边，有：

其中Si,t为第i 条边上的流量，物理意义为：取正时为大电网对i+1结点的供电量，取负时为风光储系统经过该边对电网其他结点的供电量。Pi,t为储能装置释放的功率，为正时向电网放电，为负时充电。对于决策变量Si,t，有Si,t∈[0,ui]，其中ui是第i 条边的最大流量。

电网对系统的供电量就是节点负载1、负载10的流入量。在电路理论中，常常用基尔霍夫定律对电路进行分析，其中最核心的一点是流入节点的电流量必定等于流出电流的量[3]。本文假设在复杂的电网传输系统中，这一定律依然适用。对于节点负载1、负载10来说，流出电量可以由某些边当前时刻的流量来表示，某一时刻电网对所有负载的供电量即结点负载1、负载10的流出量与节点上负载的消耗量的和，可以表示为：

考虑题目中规定的其他条件：风光一天内发电的总量不宜低于负荷用电总量的30%，不宜超过负荷用电总量的70%，可表示为：

24h 内，电网发电和风光发电的总量为：

两台变压器允许通过的最大功率分别为50MW和70MW，需满足：

除了考虑电网配置时的限制外，还要保证蓄电池里的剩余量总是大于0，可以表示为：

风电、光伏发电具有波动性和间歇性，受到天气影响时，风、光发电的有功输出会产生大幅度的波动，由于较大的波动会造成电网损坏，本文加入硬性约束条件，使得电网供电波动不超过5%。

综上所述，电网的配置问题可以写为：

其中ai、bi、ci分别为风、光、储的配置功率，q1、q2、q3分别为风光储每MW 的单价。且有：

u1t、u2t分别为风光设备的波动率，由模拟产生。

4.2 模型求解

本问题为多目标规划问题，由于已经对波动加入了硬性约束，可以采用简单线性加权的方式将两个目标合为一个。这样可以解释为：在满足波动一定的同时使得波动和成本尽量小。考察两个目标的数值大小，最终确定的优化目标为：

问题为非线性规划问题，一般可以采用遗传算法、蚁群算法、粒子群算法等智能算法求解[4]。但考虑到本文中决策变量超过千个，上述算法存在收敛速度过慢、难以收敛到全局最优点等问题，选择使用lingo 软件进行求解。

Lingo 由美国公司LINDO 推出，可以用于求解非线性规划，也可以用于一些线性和非线性方程组的求解等，是求解优化模型的优秀选择之一。

将题目中的数据带入到模型中，最终得到的配置结果为：在负载3处建立额定功率为0.321MW 的风力发电、6.018MW 的太阳能发电、52.793MWh的储能系统；负载4、5、6、7、8、9处分别建造0.0438MW、0.0444MW、9.4303MW、0.0470MW、0.0470MW、0.0470MW 的光能发电，0.3040MW、16.8516MW、0.3203MW、0.3208MW、0.3208MW、0.3208MW 的风能发电；负载11、12、13、14、15处分别建立额定功率为1.414MW、9.510MW、0.663MW、1.414MW、12.571MW 的风力发电，11、12、14、15处建立0.0166MW、0.0166MW、0.0166MW、0.296MW 的光能发电，13、15处分别建立2.665MW、11.194MW 的储能装置

从结果可以看出，系统对光能发电的需求较少，大多数发电功率在0.1MW 以内，说明光能发电不适合作为主要的发电方式。而储能装置对系统的作用较大。

5 问题二模型的建立与求解

5.1 模型的建立

问题二是在问题一得到的风光储容量配置基础上，以一天为周期，优化系统的运行出力，使得价格最少，电网输出功率最低。此时的变量为储能元件每一时刻电能的充放量和电网的供电量。由于风光储基础设施已经配置完成，整个系统运行在可控范围内。此时应该以满足负载需求为首要目标，因此将电网波动范围约束解除。结合问题一给出问题二的约束条件：

由于题目中涉及两个目标，可采用线性加权的方式将二者结合起来。主观上应该认为二者同等重要，考虑到两个函数的数值大小，可确定系数的比值。根据题中所给的电网分时电价，电网的运行成本问题可以表示为：

5.2 模型的求解

使用lingo 对本题进行求解，得到了24h 内，每一时刻每一条线路上的电流流通量，据此，可以得到电网每一时刻的出力。其中几个时刻电网的输出功率为：0时输出63.1716MW，6时输出55.5827MW，12时输出45.7550MW，18时输出65.4812MW，23时输出48.8929MW。一天内花费的电费约为97.28万元。

6 总结

本文将实际复杂的风光储电网系统简化为一个无向无环图，涵盖了实际电网系统中的多种连接方式和现实中存在的限制。通过多目标优化的思想求解得到最优配置方案。考虑到现实中变量分布具有随机性，可以根据实际参数服从的概率密度函数修改本模型的参数。

从本文得到的数据可得出结论：为满足现实中的负载，风力发电和光能发电依旧处于从属地位，难以取代电网供电。其中，光能发电设施最适合按照功率低、分布广的原则进行配置。