大流量亚微米颗粒物气溶胶精准分离器设计*

符龙熙,易礼斌,欧 强

(重庆交通大学 机电与车辆工程,重庆 400074)

0 引 言

窑洞在中国民间建筑历史中占据着极为重要的地位,它是一种历经四千多年的发展完善,依据自然地势、地质等条件形成的适宜中国西北地区气候、环境的穴居式民居建筑形态[1]。中国黄河流域的窑洞是一种特有的居住建筑样式,主要分布于甘肃、山西、陕西和河南等地区。时至今日,窑洞居住者仍然数量众多。根据古窑洞课题组调查,1949～2000年,中国的窑居总人数达一亿一千万人,截至2018年,窑洞居住者仍有近二千万人[2]。

大部分窑洞结构为拱券结构[3],该结构会导致内部通风不畅,窑筒内空气中常含有大量天然放射性气溶胶即0.5μm及以下的亚微米颗粒物,若居民吸入一定浓度的粒物,将会在体内积累强烈的辐射性,使体内各个器官发生不同程度的损伤,进而引发功能紊乱、严重时可能导致基因突变及生育能力器官衰竭甚至死亡。更严重甚至可能诱发白血病和癌症。因此需要一种大流量亚微米颗粒物气溶胶精准分离器对环境中的亚微米颗粒物进行精准分离,进而精准测量其浓度,确保居住环境的安全以及居住者的健康问题。

亚微米颗粒物气溶胶分离器是虚拟冲击器的应用之一[4],它基于惯性式原理实现微粒物的分离与富集,能显著提高气体中待测微粒物的浓度,是实现高精度核辐射颗粒物检测的重要前提,研制此新型分离器对当前的窑洞居住者和乡村振兴具有重要意义。

虚拟冲击器在气溶胶的采集方面得到了广泛的应用,并一直在改进。而提高虚拟冲击器的性能可从三个方向入手:①在相同的流量下降低压降;②减少虚拟冲击器内部的气溶胶粒子损失;③减小切割粒径[5]。随着时间推移,虚拟冲击器的性能不断优化,切割粒径范围也不断扩大,但目前绝大多数虚拟冲击器仍只能适用于小流量的颗粒物富集,无法应用于大流量工况下的颗粒物富集。

在20世纪80年代,国外学者已经开始对虚拟冲击器进行系统化和应用化的研究。在此之后,越来越多的国外研究团队对虚拟冲击器进行了深入探讨,并逐步将虚拟冲击器应用于相关设备中[6-9]。而国内对虚拟冲击器的研究和应用相对较少,而且其大多应用于低浓度气溶胶的快速采样[10],不能实现大流量工况下粒子富集。因此,工作流量与壁面损失、收集效率和切割粒径之间的矛盾无法平衡。当前市场上的虚拟冲击器的切割粒径主要为微米级别,针对亚微米级别粒子的虚拟冲击器的研究相对较少[10]。而常见的天然放射性气溶胶粒子一般粒径小于0.5 μm[11],可直接经由呼吸道进入人体而产生危害;另外,粒径越小,粒子的分子运动越明显,轨迹方程越复杂[12],越难以进行检测。因此,开展大流量亚微米颗粒物气溶胶精准分离器设计具有重要的理论价值和应用价值。

为实现对大流量亚微米颗粒物浓度检测的高精度,笔者从实际应用需求出发,设计出一种由空气旋流器、亚微米虚拟冲击器组成的大流量亚微米颗粒物气溶胶精准分离器。首先对空气旋流器、亚微米虚拟冲击器进行设计和数值模拟,并根据模拟结果提出结构优化方案。结构优化后,大流量亚微米颗粒物气溶胶精准分离器平衡了工作流量、壁面损失、收集效率和切割粒径四者间的矛盾,同时实现了大流量亚微米颗粒物浓度的精准检测。

1 结构设计

文中设计的大流量亚微米颗粒物气溶胶精准分离器设计如图1所示。其由空气旋流加速器[13]与亚微米虚拟冲击器构成。空气旋流加速器提供大流量,实现高浓度微粒的快速富集;亚微米虚拟冲击器实现微粒的精准分离。

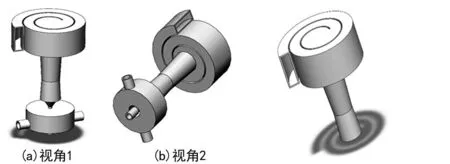
图1 精准分离器模型图2 空气旋流加速器模型

1.1 空气旋流加速器设计

空气旋流加速器的设计基于人造龙卷风抽吸原理,它主要由旋风入口、涡壳和拉法尔管三个部分构成[14],整体设计如图2所示。

根据常见的颗粒物分离器尺寸,将蜗壳出口简化为一个φ10的圆截面,同时蜗壳壁面遵循渐开线方程,空气沿着渐开线收缩,增强旋风的旋转能力,方程如下:

x=(5t1+5)cos(2πt1)

(1)

y=(5t2+5)sin (2πt2)

(2)

式中:t1=0,t2=2,2.5,3。

拉法尔管由一段渐缩管和一段渐扩管构成,渐缩管起到增大流速作用,渐扩管起到稳流作用,为亚微米虚拟冲击器提供稳定流场。

1.2 亚微米虚拟冲击器设计

虚拟冲击器一般基于Marple理论进行设计,主要设计雷诺数和Stokes数两个参数[6]。

流场的雷诺数为一个无量纲数,是流体所受惯性力与粘性力的比值,其表达式为:

(3)

式中:ρ为空气的密度;u为流体的平均速度;μ为空气动力粘度;Q0为流量大小。一般来说,当雷诺数Re>4 000时,流体的流动形式为湍流,雷诺数Re越大,湍流现象越明显,壁面损失越大。

对于亚微米粒子的运动分析时,粒子的实际运动速度比由斯托克斯定律计算出的快。因此,对亚微米粒子按式(4)进行坎宁安滑移修正:

(4)

式中:λ为气体分子自由程;Dp为气溶胶粒径。

故经过修正后的Stokes数St的表达式为:

(5)

经过上述理论计算可知,亚微米虚拟冲击器设计雷诺数为500～1 600范围内,喷嘴直径D0=0.7 mm。图3中已标示出虚拟冲击器的主要结构参数,包括入口喷嘴的孔径D0,收集孔的孔径D1以及二者之间的距离S。根据相关设计经验,一般收集孔的孔径D1取为喷嘴直径D0的1.3～1.4倍,两孔之间的距离S取为喷嘴直径D0的1.2～1.8倍,此外,还要保证两个孔的同轴度误差小于0.05 mm。

图3 虚拟冲击器的主要结构参数

2 分离器流体动力学建模

依据三维模型,抽取等效计算流体区域,主要尺寸如图4所示。

图4 等效计算流体区域主要尺寸

数值分析采用计算流体动力学程序ANSYSFLUENT进行。ANSYS FLUENT基于有限体积法,用来模拟高度从不可压缩到可压缩范围内的复杂流体流动[17]。为简化计算,将分离器分成空气加速旋流器和亚微米虚拟冲击器两部分研究,简化后的模型如图5所示。

图5 简化后流体域模型

2.1 空气旋流器数值模拟

对于空气旋流加速器主要研究其对气溶胶的加速功能,故采用单相流模型即可。用单相流模型求问题的一般步骤为:先求解连续相流场,然后研究其流动情况。

将流体的进入部分设置为速度进口,出口部分设置为自由出口。所有壁面均设置无滑移边界条件。采用不可压缩流体模型和k-ε湍流模型进行连续相流场计算,具体采用压力-速度耦合的COUPLED算法。空气的温度设置为300 K。模型共划分了20万个网格,其中速度入口和流量出口进行网格加密处理。

在求解前,设置模型的边界条件为:入口边界设置为速度入口(入口速度ve=1 m/s);流量出口为流量出口,类型为逃逸;壁面边界设置为陷入。

求解完成后,可在后处理操作中得到单相连续流体的加速情况,其蜗壳部分水平方向界面与整体竖直截面如图6、7所示。

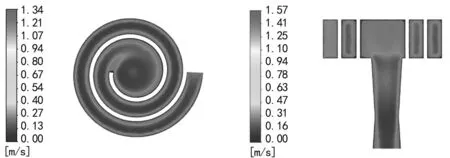
图6 蜗壳部分水平方向截面速度云图

2.2 亚微米虚拟冲击器数值模拟

对于亚微米虚拟冲击器主要研究其对气溶胶的分离情况,故采用DPM模型即可。用DPM模型求解离散相问题的一般步骤为:先求解连续相流场,然后创建离散相喷射源,最后求解单向或双向耦合流动。

气溶胶入口设置为速度入口,大流量出口与小流量出口均设置为自由出口。所有壁面均设置无滑移边界条件。采用不可压缩流体模型和k-ε湍流模型对连续相流场进行计算,并采用压力-速度耦合的COUPLED算法。空气的温度设置为300 K。模型共划分了57万个网格,其中速度入口、小流量出口和大流量出口都进行了网格加密处理。

在求解前,设置离散相模型的边界条件为:入口边界设置为速度入口(入口速度ve=2.5 m/s);大流量出口为流量出口,类型为逃逸;小流量出口边界设置为流量出口,类型为逃逸;壁面边界设置为陷入。

求解完成后,通过后处理操作可以得到粒子的运动轨迹和分布结果。如图8、9分别为0.1 μm、3 μm的粒子在经过亚微米虚拟冲击器作用的运动轨迹。其中,主要结构参数为:D0=0.7 mm、D1=0.9 mm、S=0.9 mm、Q0=0.78 g/s。

图8 0.1 μm粒子的运动轨迹图9 3 μm粒子的运动轨迹

3 分离器分离性能影响因素分析与结构优化

由于大流量亚微米颗粒物气溶胶精准分离器由空气旋流加速器和亚微米虚拟冲击器这两个独立的功能部分组成,所以在对分离器进行性能分析时,也可将分离器分成两个部分进行性能分析。

3.1 空气旋流加速器性能影响因素分析及结构优化

(1) 内壁渐开线圈数对空气旋流加速器的性能影响分析

对于空气旋流加速器的最大速度放大倍数α可用式(6)来计算:

(6)

式中:vM为气溶胶被加速后的最大速度;vin为入口气溶胶速度。

考虑到不同的入口流量对空气旋流加速器性能的影响,选取不同的入口速度,使用FLUENT程序、应用同上文中相同的方法进行数值仿真,得到气溶胶加速后的最大速度,并计算得到最大速度放大率α,结果如表1所列。

表1 模拟参数表

从表1可知,入口速度对于空气旋流加速器的最大速度放大倍数影响较小,内壁渐开线圈数对空气旋流加速器的最大速度放大倍数影响较大,且空气旋流加速器的最大速度放大倍数随着内壁渐开线圈数的增大而增大,因此在选用空气旋流加速器时,应该尽可能选取内壁渐开线圈数较多的空气旋流加速器,故所研究的空气旋流加速器内壁渐开线圈数选择3。

(2) 拉法尔管对于空气旋流加速器的性能影响分析

拉法尔管由一段渐缩管与一段渐扩管两部分组成,渐缩管用于增大气溶胶流体流速,渐扩管用于提供稳定流场。

但是,在多次不同边界数值数值模拟的过程中发现,空气旋流加速器的拉法尔管的渐扩管并不能较好地起到预期的稳流效果。以内壁渐开线圈数为3、入口气溶胶速度vin=3 m/s为例说明,其数值计算如图10所示。由图10可见,拉法尔管的渐扩管出口处流速极不均匀,出口中心轴线处产生了较大的损失,故不能为亚微米虚拟冲撞机提供稳定的流场。在渐缩管的直径最小处,流速分布较均匀,故将拉法尔管优化成只有一段渐缩管的结构。优化后的空气旋流加速器由内壁渐开线圈数为3的蜗壳、渐缩管和旋风入口三部分构成。

经过优化后的空气旋流加速器数值计算结果如图11所示。边界条件设置与上文相同。由图11可见,经过优化后的空气旋流加速器出口流场损失较小,能为亚微米颗粒物旋流加速器提供较稳定的流场。

3.2 亚微米虚拟冲击器性能影响因素分析及结构优化

入口结构对空气旋流加速器的性能影响较大,故需对其进行分析计算。

在入口流量Q0=4.5 L/min时,对于0.1 μm的亚微米颗粒物分离效果良好。随着流量增大,雷诺数Re也会增大。

若入口流量Q0提升至700 L/min或者更高,由式(3)可知,则Re≫4 000,因而会产生分离失效的问题,粒径为0.1 μm的亚微米颗粒物会全部从小流量出口流出。因此需对入口结构做出改进,改进后的结构如图12、13所示。

图12 入口结构优化三维模型

在入口处增加一个圆环形排气口并增加两个小流量出口,同时将小流量出口直径φ从原来的3 mm提升至5 mm,这样的优化能够使小流量出口在大流量工况下起到良好的泄压作用,提升出流效果,增加的圆柱形圆环高h=4 mm,圆环外径r1=21 mm,圆环内径r2=9 mm。此时的入口总流量为Q0;入口速度为v0;横截面积半径为r0,进入亚微米虚拟冲撞机的待测气体流量为进气流量Q1,速度为v1,排气口速度为v2,进气口半径为r3。入口流量Q0、进气口流量Q1、排气口流量Q2三者存在如下式关系:

Q1=Q0-Q2

(7)

流量Q与流速v之间的关系为:

Q=vA

(8)

式中:A为流量Q通过的横截面积。

故式(7)可展开为:

(9)

入口流量设置为700 L/min,结构优化后,能够显著提升亚微米虚拟冲击器在大流量工况下的粒子分离效果,亚微米虚拟冲击器流场纵截面流速云图和粒径为0.1 μm的亚微米颗粒物的分离效果如图14、15所示。

图14 亚微米虚拟冲击器流场纵截面速度云图

4 结 语

亚微米颗粒物气溶胶分离器是实现高精度检测核辐射颗粒物浓度的前提。文章设计了一种大流量亚微米颗粒物气溶胶精准分离器。基于理论基础和流体动力学方法,设计并仿真分析了两大组成构件,探究了空气旋流加速器的速度放大系数与亚微米虚拟冲击器的分离效果。给出了空气旋流加速器的具体优化参数,同时对亚微米虚拟冲击器的结构进行了优化,优化后其在700 L/min及以上的大流量工况下实现了对粒径为0.1 μm的亚微米颗粒物有效分离。文章的研究证明了在设计大流量亚微米颗粒物气溶胶精准分离器时,采用流体动力学分析方法的可行性,这为后续优化设计以及推进辐射颗粒物分离技术的发展奠定了基础。