基于对流扩散方程的水质预测模型研究

张晨璐， 宋金玲， 康燕， 张经武， 樊刘炎

（河北科技师范学院 数学与信息科技学院 河北省农业数据智能感知与应用技术创新中心，河北 秦皇岛 066004）

水是人类赖以生存的生命源泉， 随着工农业的快速发展， 水污染问题日益突出， 水污染对社会造成了一系列的危害， 不仅对农作物和水产造成了巨大影响， 对人类的身体健康也危害颇深。 因此， 为了实现水污染的及时监督治理， 对水质进行预测预警研究意义重大。

近年来， 随着计算机以及预测技术的发展， 对于水质预测的研究日益多元化， 目前研究成果主要包括基于统计回归的水质预测模型［1］、 基于ARIMA 的水质预测模型［2－3］、 基于支持向量机的水质预测模型［4］、 基于神经网络的水质预测模型［5－7］。但是， 这些研究都是基于特定点位的历史水质数据预测该点位未来一段时间的水质变化， 即在时间维度上进行水质预测［8－9］。 目前的河流水质监测中，限于经费问题， 监测设备的布设一般比较稀疏， 未布设监测设备位置的水质情况则无法及时掌握， 不利于水污染事件的及时发现和治理。 因此， 为了实现河流水质的细粒度监测， 基于已知的监测点位数据， 预测出河流中其他位置的水质情况具有重要研究意义。 本研究基于流体力学的对流扩散方程， 对河流上无监测设备位置的水质变化情况进行空间维度预测， 以期实现河流水环境的细粒度监测， 为环保部门和相关工作人员的水污染治理提供决策支持。

1 水质对流扩散方程

根据水中污染物的时间推进和空间上的输移、扩散规律， 形成了不同的水质模型， 并应用于水体污染物迁移扩散预测分析［10－12］。 按照系统内参数的空间分布特性， 水质模型可以分为一维、 二维和三维模型。 按照水质参数的转移特性， 水质模型又分为随流模型、 扩散模型和随流扩散模型（或对流扩散模型）。 对于河流来说， 如果河流的深度和宽度远小于长度， 其在垂向和横向的污染物浓度梯度可忽略不计， 这种情况下对河流不同点位的污染物浓度计算可以简化为一维水质模型。 且由于污染物在水体的迁移与转化过程中产生了分子的扩散， 在这种情况下一般考虑使用一维对流扩散方程来模拟污染物的迁移扩散， 如式（1）所示为一维对流扩散方程。 水质预测模型的建立过程， 是在选定的污染物输移数学模型基础上， 结合已知的参数和初始边界条件， 从而来预测水体环境中污染物时空分布状况的。

式中： u 为流速， km·h－1； E 为扩散系数，km2·h－1； K 为污染物的衰减系数， h－1； c 为污染物质量浓度， mg·L－1。

式（1）的一维对流扩散方程属于偏微分方程， 目前对一维对流扩散方程最常用的数值解法是有限差分法［13－14］， 有限差分法具有精度高、 涉及网格点少的优点。 有限差分法又分为显式差分法和隐式差分法， 显式差分根据差分形式不同又细分为前向差分、后向差分和中心差分。 而对于整个有限差分法的求解过程则是利用离散的网格节点来取代连续的求解区域， 通过在每个离散的网格节点上进行泰勒展开，将方程中的各阶导数用差分表达式来近似表示， 再求解差分方程组便可得到偏微分方程的最终解。

差分的精度是以泰勒展开式近似值中误差项的Δx 阶数为准， 通过对各种差分的泰勒展开式对比可知， 前向和后向差分均为一阶精度、 中心差分是二阶精度， 说明中心差分比前向和后向差分的精度更高。 另外， 虽然显式差分法的形式比较简单， 但是在很多状况下计算时间相对较长， 现有文献显示隐式差分解比显式差分解更加稳定、 精确、 逼近真解［15］。 综合上述分析， 本次试验选用显式中心差分法和隐式差分法分别对污染物浓度进行预测， 下面对2 种方法的求解精度进行验证。

2 对流扩散方程求解及精度验证

现以某河流的水质数据对对流扩散方程的不同求解方法进行验证， 已知该河流在x ＝0 处有一个排放1 h 的点源， 该河流的u ＝5 km／h， E ＝2 km2／h， K ＝0.151 h－1， 令时间步长Δt ＝0.1 h， 空间步长Δx ＝0.5 km， 且初始时刻的上游边界x ＝0 处的污染物质量浓度为10 mg／L（监测站点监测的数据），下游边界x ＝10 km 处的污染物质量浓度为0， 通过以上条件对每个时间步各节点的污染物浓度进行模拟。 本次试验将监测站点检测到的污染源排放结束1.5 h 后部分节点的污染物（总氮）监测值， 和对流扩散方程各种解的模拟值进行对比， 各节点的实测值具体如表1 所示。

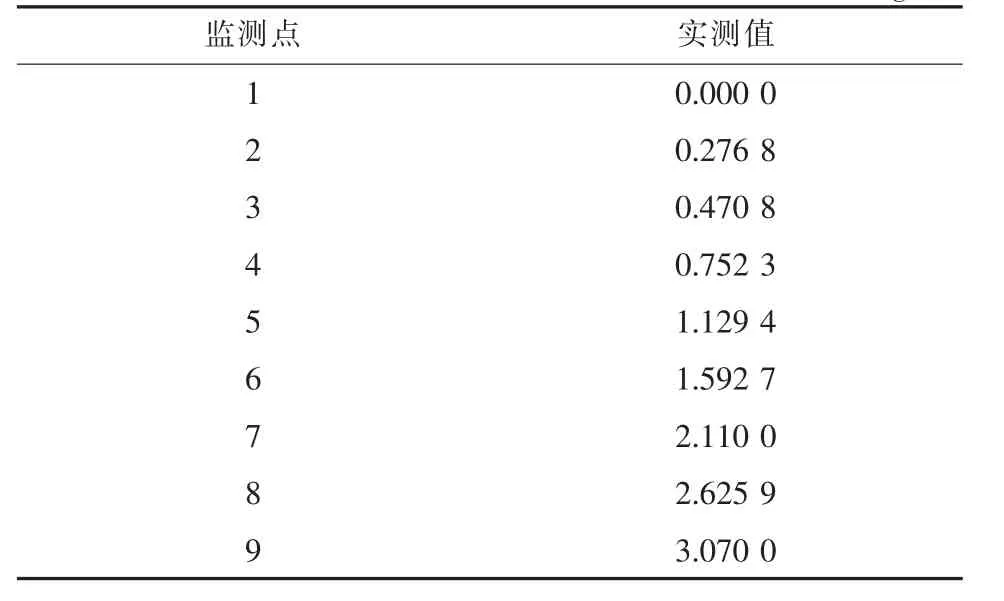
表1 各监测点实测值Tab.1 Measured value of each monitoring point mg·L－1

2.1 显式差分法求解

根据求解偏微分方程的近似计算中利用差商代替微商的原理， 式（1）可以近似地用差分表示， 其中对x 的一阶偏微分可用前向差分表示为：对x 的二阶偏微分可用中心差分表示为：用前向差分代替和， 用中心差分代替后， 将同类项进行合并， 式（1）可近似地表示为式（2）的差分方程：

由式（3）可知， 节点i 的下一时间步的浓度值需由当前时间步的i－1， i， i＋1 三个节点的污染物浓度求得， 因此， 若想求n＋1 时间步N 个节点的浓度值， 则需要从第1 个时间步开始， 分别利用N个式（3）的方程求出下一时间步的各节点污染物浓度， 逐步迭代求出（） 后才能求得第n 个时间步各节点的污染物浓度值。 因此， 为了更方便地对各个时间步下各节点的污染物浓度值进行求解， 可将式（3）表达成下式的矩阵形式。 根据式（4）和各已知条件， 按照时间步依次迭代可以求得每个时间步下各节点的污染物浓度， 从而得到原问题在求解域上的近似值。

根据上面式（4）的矩阵， 可以编程迭代求解出每个时间步各节点的污染物浓度， 排污结束1.5 h后各节点污染物浓度模拟值如表2 所示。 通过与监测站点监测到的实测值进行对比， 模拟值与实测值的拟合度为0.510 2， 对比发现从第6 个节点开始模拟值和实测值相差较大， 原因可能是显式中心差分法适用于顺直天然河流， 而该河流并不是顺直河流， 存在地势落差和弯曲等情况， 导致显示差分法的求解精度较低。

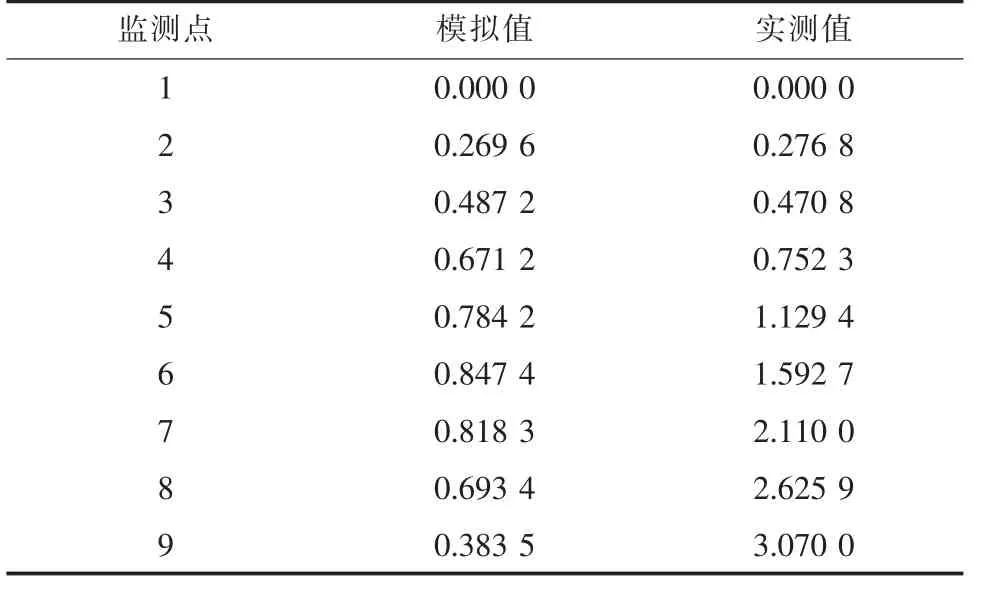
表2 显式差分模拟值与实测值对比Tab.2 Comparison of explicit differential analog values and measured valuesmg·L－1

2.2 隐式差分法求解

隐式差分法和显式差分法中求解偏微分方程的近似计算原理一致， 式（1）可以近似地用差分表示，其中对x 的一阶偏微分可用前向差分表示为：＝； 对x 的二阶偏微分可用中心差分表示为：用前向差分代替和， 用中心差分代替后， 将同类项进行合并，合并同类项最终得到的隐式差分方程如式（5）所示：

式（7）的三角矩阵一般采用Thomas 方法进行求解， 它是基于高斯消元法的算法， 算法分为2 个阶段： 向前消元和回代。 Thomas 方法可以通过编程实现， 从而计算得到隐式差分法下空间维度各节点的水质数据。 排污结束1.5 h 后各节点的污染物浓度模拟值如表3 所示， 模拟值与实测值之间的拟合度达到了0.748 1， 虽然各个监测点的模拟值与实测值也存在着一定的误差， 但是试验结果表明， 随着时间步的减小， 实测值与模拟值之间的误差也在逐渐缩减， 说明隐式差分法的模拟值更加接近实测值。

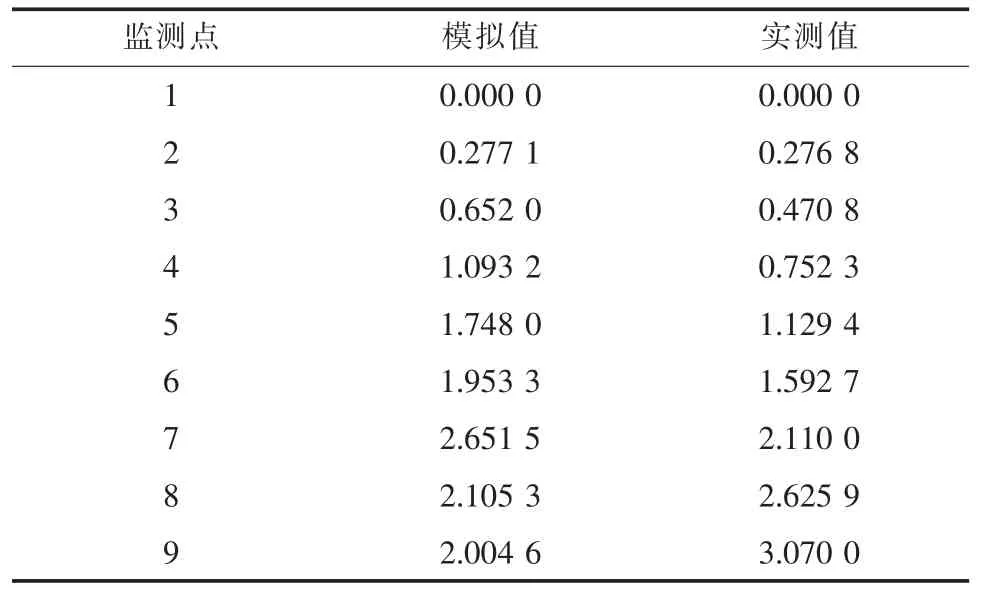
表3 隐式差分模拟值与实测值对比Tab.3 Comparison of implicit differential analog values and measured valuesmg·L－1

2.3 解析法求解

解析法通常用来求解非线性方程的解， 能有效地提高准确度和计算速度。 解析法是从对流扩散方程解析出给定条件下物质分布的解， 利用解析法可以求解任意初值问题， 方程的解中包含位置和时间。 解析解的求解方法有2 种： 一种是采用不定积分法求解； 另一种是采用渐进分析法求解。 不定积分法是个求解微分方程的过程， 而渐进分析法则是划分为几个渐进步骤， 每一步都可以求得近似值，依次不断迭代， 最终求得近似解。 渐进分析法的对流扩散方程解析解如式（8）所示。

其中， 初始条件为c（x，0）＝Mδ（x）， 边界条件为c（±∞，t）＝0， ∂c（±∞，t）／∂x ＝0。 t 和x 分别表示时间和空间位置， u 表示流速， D 表示扩散系数，M 表示河流排放污染物的总质量， 本试验中排放污染物的总质量M ＝15.77 mg（通过已知的各节点污染物浓度拟合计算求得）。

通过编程计算式（8）求得解析解， 同样将排污结束1.5 h 后各节点的污染物浓度模拟值与实测值进行对比， 如表4 所示。 通过对比分析， 实测值与模拟值之间的拟合度达到了0.918 5， 且相关系数为1.000 0， 说明解析解的模拟值与实测值基本上比较接近， 因此有的文献也将污染物扩散的解析解作为实测值使用［16］。

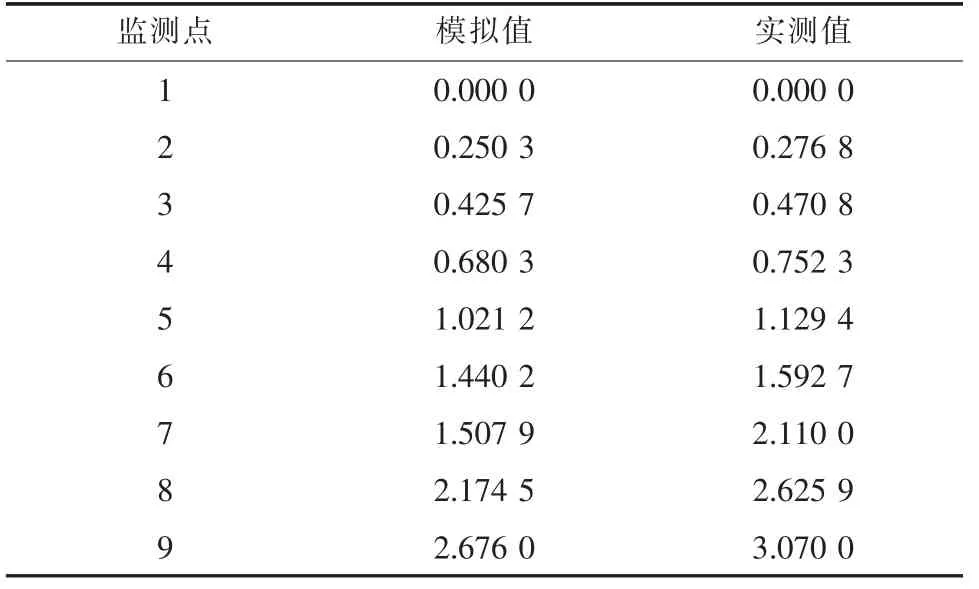
表4 解析解模拟值与实测值对比Tab.4 Comparison of analytical solution analog values and measured valuesmg·L－1

2.4 求解方法对比及分析

通过上面3 种对流扩散方程求解方法的对比结果发现， 解析解的模拟值与实测值之间的误差最小， 说明解析解的精度最高、 最接近实测值， 其次是隐式差分法， 最后是显示差分法。 解析法得到的模拟值与实测值的相关系数也最高， 说明解析法比隐式差分法的稳定性高， 隐式差分法又比显式差分法稳定性高。 另外， 用解析法求解过程中， 污染物总质量M 是一个已知参数， 而实际情况下很难获知污染源的排污总量， 因此使用解析法的条件比较苛刻， 不过在污染物总质量M 能拟合求解的情况下则可以使用该方法。 隐式差分法的求解过程只需要知道几个必须的参数便能进行计算， 且计算快速、 计算精度比较高， 因此隐式差分法比较适合实际使用。 综合3 种求解方法的特点， 在下面的水质预测应用中， 由于缺乏各时间步各节点的实测值，将解析解模拟值作为实测值使用， 采用隐式差分法对各节点的污染物浓度进行预测。

3 对流扩散方程应用

在实际河流中应用对流扩散方程， 采用隐式差分法求解污染物浓度， 与解析法模拟的实测值进行对比。 由于上述试验已经证明了隐式差分法比显示差分法的精确度更高， 更接近实测值， 其可行性更高， 且文献［16］也表明了隐式差分法的高效可行性， 而对于污染物总质量M 的验证在文献［17］中已经证明了其拟合求解方法的有效性， 利用拟合的污染物总质量M 求解解析解可行， 而将解析解模拟值作为实测值使用也是目前一些文献［16，18］的常用方法， 因此， 利用拟合污染物总质量M 求得解析解将其作为实测值， 并与隐式差分法进行对比的方法具有一定可靠性。

3.1 研究区概述

本次试验以木兰溪流域为研究区， 利用对流扩散方程进行水质预测。 木兰溪流域位于福建省沿海中部， 地势自西北向东南沿海倾斜， 上游西北部龙岩峰为最高， 海拔1 267 m。 流域呈扇形， 西部和北部以山地为主， 低山、 峡谷、 盆地错杂其间， 中部和东部为冲积平原和海积平原。 木兰溪干流总长105 km， 自源头至仙游溪口大桥长28.7 km， 溪口大桥至木兰陂长50.5 km， 平均坡降为1.41‰。

由于整个木兰溪流域由西北向东南存在高山、盆地、 平原等地势地貌， 受流域地势和各支流汇入的影响， 导致不同河段的流速、 污染物扩散系数等参数会有所变化， 而且该河流的整体走向比较曲折不属于顺直河流， 如果对整个河流采用一个对流扩散方程进行预测， 可能导致模拟的污染物浓度出现较大误差， 甚至不满足顺直河流的变化趋势而失效。 综合以上各种因素， 决定按照木兰溪的地势及支流汇入情况， 对河流分段建立对流扩散模型， 对相应河段的污染物浓度进行预测， 以减小模拟值与真实值之间的误差。

3.2 水质预测模型构建

通过分析整个木兰溪流域， 发现其干流有7 个主要支流汇入， 各支流汇入点均布设了监测设备（有水质监测数据）， 考虑到支流可能有污染物汇入干流， 而且河段地势的不同会导致水文参数不一样， 从而影响预测模型， 因此将支流汇入干流的交叉口作为分段点。 每个河段的起点可以看成一个连续稳定的污染源， 对每个河段分别构建对流扩散水质预测模型， 根据每个水质预测模型的隐式差分解， 将上下2 个监测点的污染物浓度作为边界条件代入到差分方程中， 就可以求得每个河段内某时间步不同空间步节点的污染物浓度预测值。 由于每个河段只是具体的流速、 扩散系数和衰减系数不同，污染物浓度的模拟过程和计算过程及计算公式完全相同， 因此以某段为例， 利用对流扩散方程对污染物的浓度变化进行模拟。

已知该段的长度大约为4 km， 该段起点的污染物（总氮）质量浓度为10 mg／L（监测站点监测的数据）， 持续时间为1 h， 因此可将该起点看作排放1 h 的污染源， 该段终点的污染物质量浓度为6.8 mg／L（为1 h 后监测值）。 由人工测量得到的该段水文参数分别为： u ＝6 km／h， E ＝3 km2／h、 K ＝0.03 h－1， 取时间步长Δt ＝0.05 h， 空间步长Δx ＝0.5 km。

由于本试验中的污染源数据只有排放浓度， 为了使用解析法求解各时间步各个节点的污染物浓度， 首先需要拟合计算污染物排放总质量M， 已知在污染源排放0.75 h 后该段的各个节点污染物浓度已经监测（如图1 所示）， 将各节点的监测值拟合成一个污染源的排放量函数， 进一步对排放量函数进行定积分求解得到M ＝35.26 mg。 将M ＝35.26 mg和其他已知条件代入式（8）， 可以求得各时间步各节点的污染物浓度， 并在下文作为实测值使用， 其中将表5 中排污结束1.5 h 后的各节点污染物浓度值作为对比数据。

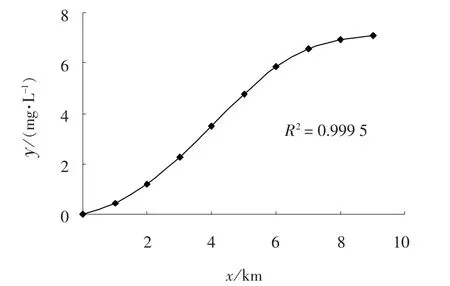
图1 污染源排放量拟合函数Fig.1 Pollution source emissions fitting function

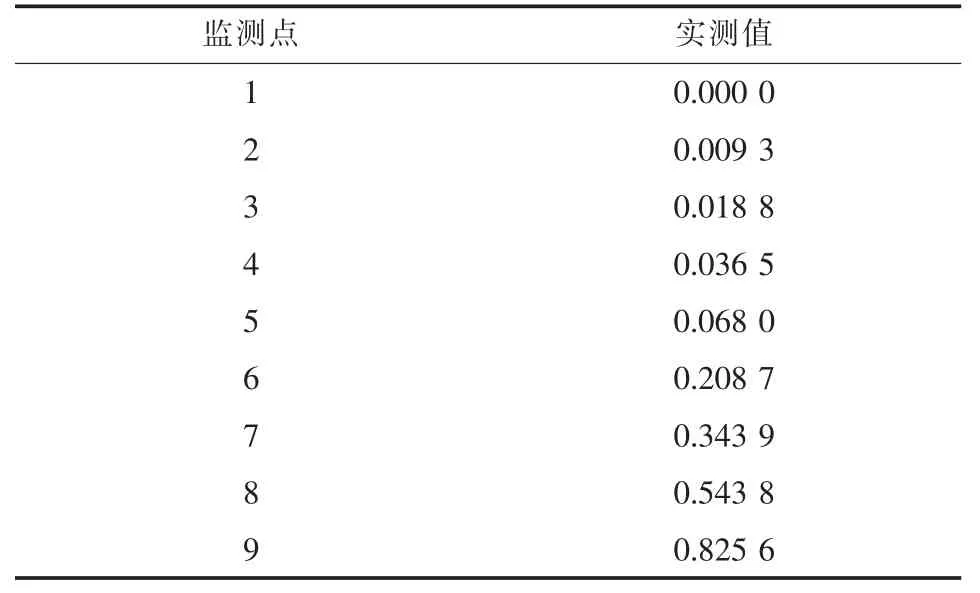
表5 利用解析解求得的污染物浓度Tab.5 Pollutant concentration obtained by analytical solutionmg·L－1

根据该段起、 终监测站点的污染物浓度， 以及该段的流速、 扩散系数、 衰减系数、 时间步长、 空间步长等数据， 利用隐式差分法计算出该段排污结束1.5 h 后各节点的污染物浓度， 模拟结果如表6所示。

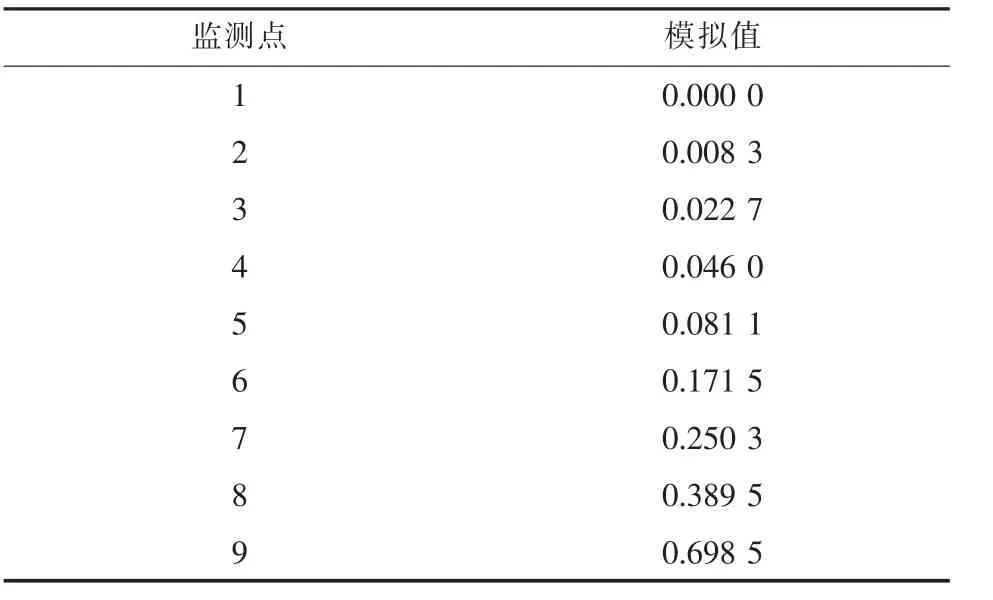
表6 隐式差分法模拟值Tab.6 Analog values of implicit difference decomposition methodmg·L－1

通过对比分析表6 的数据发现， 隐式差分法计算得到的模拟值比较接近实测值， 拟合度较高、 误差较小， 由于解析解中的污染源排污总质量为拟合求得， 与实际排污量本身存在误差， 而且实际河流中污染物的扩散与支流汇入以及河道坡度的升降均有明显关系， 解析解模拟值和实测值存在一定误差属于正常现象， 因此利用隐式差分法预测的各节点污染物浓度基本符合自然河流的水质情况。

4 结论

本次试验利用对流扩散方程进行了空间维度的水质预测， 并将其在木兰溪流域进行了应用。

（1） 通过试验将对流扩散方程的显式差分法、隐式差分法和解析法的求解精度进行了对比分析，验证结果表明解析法高于隐式差分法、 隐式差分法高于显式差分法。

（2） 在木兰溪流域的实际应用中， 对木兰溪干流分段建立了对流扩散预测模型， 并以解析法计算的各时间步各节点的污染物浓度值作为实测值， 与隐式差分法计算的模拟值进行了对比。 通过应用可知采用隐式差分法进行空间维度预测具有一定可行性， 但是还需要进一步提高预测精度。

（3） 利用解析法预测在实际应用中虽然存在一定难度， 但是在污染源排污量已知或者可以拟合获知的情况下， 具有较好的应用效果。