基于需求响应的电力负荷预测与建模研究

宋振培, 张少迪, 周品品

[1.上海电力大学, 上海 200090; 2.上海电器科学院研究所(集团)有限公司, 上海 200063; 3.上海市智能电网需求响应重点实验室, 上海 200063]

需求响应是指电力市场用户响应市场价格信号或激励措施,改变传统用电模式的市场参与行为。在电力现货市场竞争中引入需求响应,对资源进行协调优化是适应电力现货市场发展的必然要求。科学、准确的电力负荷预测是优化调度方案和发电计划的基础。近年来,大规模间歇性新能源发电系统并网,新型负荷的广泛接入,以及需求响应不确定性等问题,给电力负荷带来了更高的随机性和动态性,对电力负荷预测的准确性和时间尺度提出了更高的要求[1-6]。如何在长时间序列电力负荷预测中提高电力负荷预测模型的准确性,是当前重要且新颖的一个研究方向。

常用的电力负荷预测分析方法主要分为两大类:第1类是以数理统计为基础的传统负荷预测方法;第2类是以深度学习为代表的智能负荷预测方法。第1类方法主要是根据历史负荷数据建立预测对象的函数模型。文献[7]采用优化后的差分整合移动平均自回归(Autoregressive Integrated Moving Average,ARIMA)模型进行电力负荷预测,预测结果的准确度可以达到神经网络的预测水平,但是时间序列方法对电力负荷的平滑性要求较高,如果电力负荷受到其他不稳定因素的影响,预测效果就达不到相应的精度,甚至大打折扣。文献[8]基于灵敏度分析选择了多元非线性回归模型的关键变量,获得了高精度的制冷负荷预测结果。为了提高预测精度,文献[9]提出了一种由蚂蚁狮子优化器(1,1)确定参数的滚动机构优化灰色模型,并用电力负荷数据集进行验证。然而,由于电力负荷的非线性特性,第1类方法的预测精度较低。第2类方法是以深度学习为代表的智能负荷预测方法,由于其强大的非线性拟合能力,所以能够较好地完成电力负荷预测任务[10-12]。文献[13]将支持向量机(Support Vector Machine,SVM)用于电力负荷预测,得到了比BP神经网络(Back Propagation Natural Network,BPNN)更好的预测结果。文献[14]提出了一种核组合SVM的预测模型,与传统SVM模型相比,预测精度得到了很大的提高。文献[15]开发了一种基于模糊逻辑的专家系统,将其应用于电力负荷预测。文献[16-17]采用粒子群优化(Particle Swarm Optimization,PSO)算法对神经网络进行了优化,解决了传统BPNN收敛速度较慢的难题。然而,常用于电力负荷预测的递归神经网络(Recurrent Netural Network,RNN)由于点与点之间的路径较长,故存在难以捕捉长时间序列模式的局限性。

RNN或长短期记忆(Long Short-Term Memory,LSTM)神经网络是该领域使用最广泛的深度学习模型之一,原因是RNN或LSTM是一种以序列数据为输入并沿序列方向循环的神经网络,在序列数据的非线性特征学习方面优于其他类型的神经网络。因此,许多基于LSTM的短期负荷预测(Short Term Load Forecasting,STLF)模型被开发使用[18]。文献[19]提出了一种新的深度池化RNN模型,用于家庭层面的STLF,其在均方根误差(Root Mean Square Error,RMSE)方面优于经典深度RNN模型。文献[20]提出了一种基于LSTM的模型,通过考虑季节、天数和间隔数据预测未来15 min的负荷。文献[21]结合LSTM和自注意力机制进行了日前住宅负荷预测。此外,一些研究试图将RNN或LSTM与卷积神经网络(Convolutional Neural Network,CNN)相结合,以提高负荷预测的精度。这些模型使用CNN提取局部特征,然后将结果平面化并反馈到LSTM层。文献[22]提出了一种集成深度学习模型,将CNN和LSTM结合起来用于设备级的STLF。文献[23]开发了一个使用CNN和双向LSTM的统一客户级STLF框架。这些模型的预测结果验证了CNN层能够从多个变量中提取有效特征,从而提高基于RNN模型的负荷预测性能。

然而,从时间序列的角度来看,LSTM不能保持长期记忆[24],难以设计以长负荷序列为输入的基于RNN或LSTM的预测模型,并且无法从长负荷序列数据中捕获长期依赖关系。最近,基于注意力的深度学习模型,在捕获长期依赖关系方面表现出比RNN或LSTM模型更好的性能[25]。但自注意力机制的时间复杂度和内存使用量为零(l2),限制了其在长序列特征学习中的应用。为了解决这个问题,文献[26]提出了一种高效的基于Transformer的Informer模型。它通过设计一种称为ProbSparse的自注意力机制,将自注意力机制的复杂性降低到零(LlogL)。在这种机制中,只考虑一部分主导查询并包括在注意力计算中。由于电力负荷消耗数据是一种长时间的周期序列,Informer的ProbSparse自注意力机制可能会忽略负荷曲线的周期性特征。为了解决这一问题,本文提出了一种将Informer模型与历史惯性(Historical Inertia,HI)模型融合的HI-Informer模型,并将HI-Informer模型与Informer模型、LSTM模型、RNN模型、多层感知(Maltilayer Perception,MLP)模型进行实验对比。实验结果表明,HI-Informer模型在电力负荷预测中表现出色,负荷预测精度高于其他模型。

1 相关理论介绍

1.1 Informer模型简介

Transformer在捕获长期依赖关系方面显然比RNN具有更高的性能。然而,Transformer存在长输入序列下堆叠层的内存瓶颈、自注意力机制的二次计算复杂度高,以及预测长输出时推理比较缓慢等问题。Informer模型通过改进Transformer结构,解决了自注意力机制中的稀疏性问题:首先,采用稀疏自注意力机制,压缩注意层卷积池,降低时间复杂度和内存占用;其次,利用自注意力机制减少网络参数和维数,接受长时间序列输入;最后,采用生成式解码器,得到长时间序列的输出结果,有效提高预测精度。Informer模型由编码器和解码器组成。其中,编码器用来获取原始输入序列鲁棒性的长期依赖关系,解码器进一步实现序列预测。Informer模型整体框架如图1所示。

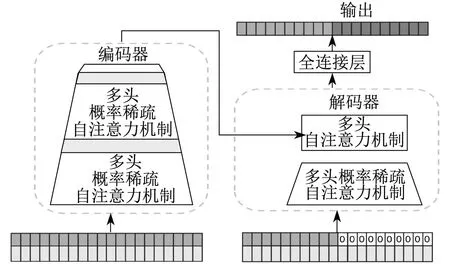
图1 Informer模型整体框架

Informer模型编码器的输入由t个特征变量、t个局部时间戳、t个全局时间戳组成。Q,K,V为输入特征变量线性转换后得到的3个相同大小的查询矩阵、键矩阵和值矩阵。Q∈RLQ×d,K∈RLK×d,V∈RLV×d,d为输入维度,LQ,LK,LV分别为Q,K,V的行维度。多头概率稀疏自注意力机制模型O的计算公式为

O=Attention(Q,K,V)=

(1)

式中:Attention(·)——注意力函数;

softmax(·)——激活函数。

为了压缩特征维数并提取优势注意,编码器采用自注意力蒸馏技术,通过卷积和最大池化减少维数和网络参数。经过多次多头概率稀疏自注意力和自注意力蒸馏,编码器最终输出特征映射。

从j层到j+1层的蒸馏过程为

(2)

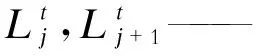
max Pool(·)——最大池化函数;

ELU(·)——激活函数;

Convld(·)——一维卷积函数;

[]AB——自注意力模块。

为了一次性输出所有预测结果,Informer模型解码器采用并行生成解码器机制。其中,输入由t-k个特征变量、k个占位符0以及对应的t个局部时间戳和t个全局时间戳组成。通过带掩码的多头概率稀疏自注意力机制运算后,利用编码器输出的特征图进行多头自注意力机制运算。最后,通过全连接层调整数据输出的维度,可以一次性输出研究者想要的所有预测结果。其中,t代表一个输出长度,k代表一个预测长度。

1.2 HI模型简介

传统的时间序列预测方法通常关注时间序列数据中的趋势、周期性和季节性等因素。然而,时间序列中的历史信息本身包含有价值的信息。这种历史信息的保持和延续被称为HI。本文引入HI模型[27]与Informer模型结合。HI模型的具体原理如下。

时间预测序列:在时间t,给定一个输出长度Lx的时间序列X(t)为

X(t)={X1(t),X2(t),X3(t),…,XLx(t)}

(3)

式中:Xi(t)——在第i个时间戳观察到的单变量(dx=1)或多变量(dx>1),i=1,2,3,…,Lx。

(4)

时间序列预测目标是提前Δ步预测对应长度Ly的序列Y(t),为

Y(t)={Y1(t),Y2(t),Y3(t),…,YLy(t)}

(5)

式中:Yi(t)=[yi,1(t),yi,2(t),yi,3(t),…,yi, dy(t)]∈Rdy。

HI以输入序列X(t)的子序列预测长度Ly为预测结果。HI作用示意如图2所示。

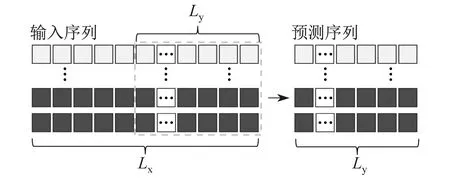
图2 HI作用示意

规范的数学表示为

(6)

2 HI-Informer电力负荷预测模型

电力负荷数据是一系列复杂的不连续时间序列,受多种环境因素的影响。对于电力负荷数据预测,首先,使用Informer模型提取序列特征并预测未来的电力负荷数据;然后,使用HI模型预测未来序列;最后,使用最小二乘法拟合Informer和HI模型的权重系数,使得混合HI-Informer模型的预测结果与实际数据之间的差异最小。将Informer模型的输出序列定义为I(t),HI模型的输出顺序定义为H(t),最小二乘法将两者的权重系数分配为w1,w2。HI-Informer模型框架如图3所示。

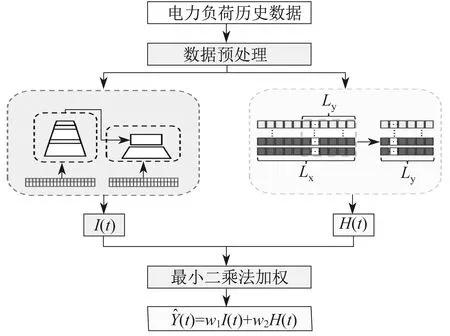
图3 HI-Informer模型框架

(7)

w1+w2=1

(8)

为了使HI-Informer模型的预测结果与实际结果之间的差异最小化,将距离函数定义为预测结果与实际结果之间的双范数,并选择合适的权重系数w1和w2使双范数最小化。双范数是w1和w2的函数,i∈T表示计算权系数的时间集,T为验证集时间的集合。双范数最小化的计算公式为

(9)

Y——真实序列;

Ii——第i个时间戳的输出值;

Hi——HI模型第i个时间戳的输出值。

为了更好预测未来数据,将训练集拆分为新的训练集和验证集,分别对w1和w2求式(7)的偏导数,得到:

(10)

(11)

w1+w2=1

(12)

权重系数w1和w2可由式(8)～式(10)联立求得,为

(13)

通过最小二乘法将HI模型和Informer模型的预测结果进行加权融合,使其能够显著减小预测误差,提高整体预测的可靠性和准确性,增加系统的稳定性,降低对特定模型的依赖,从而在不同情况下保持高性能。此外,加权融合方法非常灵活,可以根据任务需要进行定制。

3 实验过程与分析

3.1 数据准备

实验数据来自新加坡的电力负荷数据。数据包含2020年1月1日至2022年12月31日321个用户的用电量,采集间隔为1 h,数据总数为2.7万个。某用户历史用电负荷如图4所示。

图4 某用户历史用电负荷

3.2 实验结果对比

5种电力负荷预测模型实验结果对比如图5～图9所示。

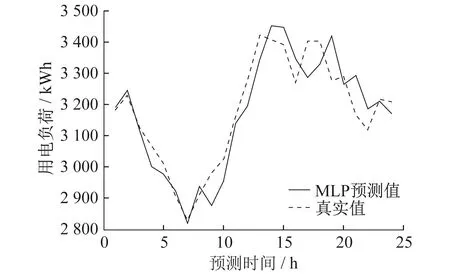
图5 MLP模型预测值与真实值

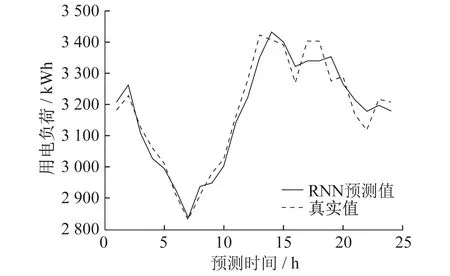
图6 RNN模型预测值与真实值

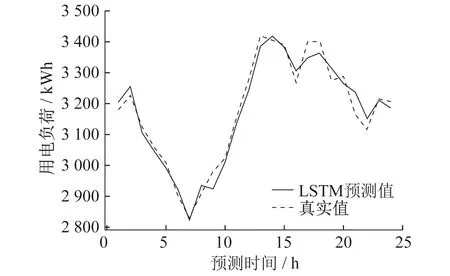
图7 LSTM模型预测值与真实值

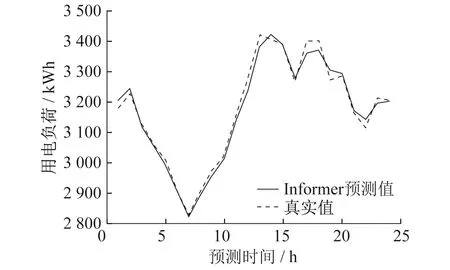
图8 Informer模型预测值与真实值

图9 HI-Informer模型预测值与真实值

从图5～图9中的模型预测值与真实值对比可以看出,HI-Informer模型的预测值与真实值非常接近,几乎完美匹配负荷波动的趋势和季节性变化。这表明HI-Informer模型在捕捉电力负荷数据中的复杂模式和周期性方面表现出色。相比之下,其他模型在某些时段中出现了明显的误差,未能捕捉到相同的趋势。

3.3 实验结果分析

在本次研究中,使用平均绝对误差EMA、均方误差EMS、对称平均绝对百分比误差ESMAP和运行时间评估模型的预测性能。EMA是回归任务的基本评价指标。相比EMA,EMS对异常值更为敏感。ESMAP是一种基于百分比误差的精度度量,能更好地评价模型预测的准确性。具体定义为

(14)

(15)

(16)

yn——预测流量值;

N——预测总数,即预测序列长度。

在相同数据集上,将本文提出的HI-Informer模型与Informer模型、LSTM模型、RNN模型、MLP模型进行对比实验。模型评价结果如表1所示。

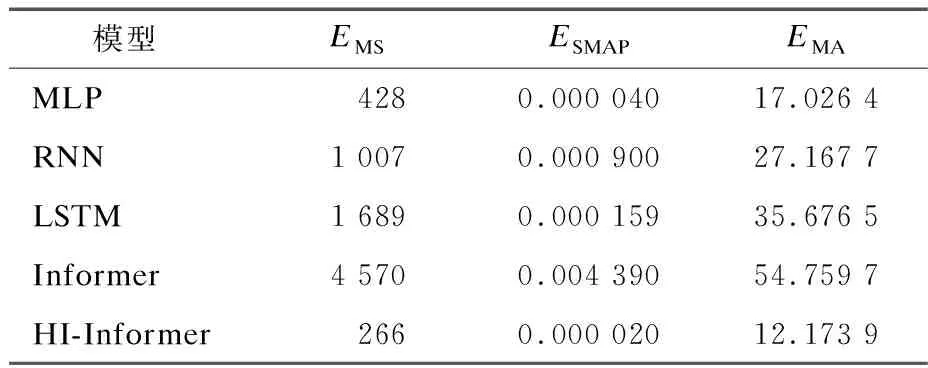
表1 模型评价结果

通过比较不同模型误差值发现,HI-Informer模型表现最佳,其平均预测误差最小。这表明HI-Informer模型在处理电力负荷预测任务时具有明显的优势。

4 结 语

本文进行了电力负荷预测任务的对比实验,特别关注了HI-Informer模型在电力负荷预测中的性能。实验结果表明,HI-Informer模型在电力负荷预测任务中表现出色,在平均绝对误差EMA、均方误差EMS、对称平均绝对百分比误差ESMAP上表现突出,具有更低的误差值。这表明HI-Informer模型在处理长时间序列数据方面具有优越性,能够更好地捕捉电力负荷趋势和季节性变化。