基于麻雀搜索算法的GDP增长率预测模型研究

马长发,马子薇

新疆财经大学统计与数据科学学院,新疆 乌鲁木齐 830012

0 引言

GDP增长率可以反映出一个国家的经济情况,它直接影响国家的宏观调控政策,同时影响金融、非金融公司的有关决策。如何准确、高效地对GDP增速进行预测,是值得关注及深入探讨的课题。因此,研究基于统计数据的季度GDP增速高精度预测方法,揭示其变化规律,对我国宏观经济决策有着重要的现实意义。

一直以来,国内外学者在对GDP进行预测时,主要采用的是灰色预测模型、自回归预测模型、移动平均法等传统的时间序列预测模型,国外学者Box et al.[1]在1976年所提出的自回归移动平均(ARIMA)模型是时间序列线性预测的典型代表。国内学者华鹏 等[2]确立ARIMA(1,1,0)模型对广东省GDP进行短期预测,为政府部门制定经济计划提供了依据和参考。传统时间序列方法要求时序数据稳定,并对复杂的非线性系统拟合能力较差,且易发生多重共线性,导致预测精度不够准确。近年来,机器学习算法对于体量大、不确定性强的数据显示出了比传统模型更好的预测效果,因而被广泛应用于经济数据的预测。黄卿 等[3]利用机器学习方法中的BP神经网络、SVM、XGboost算法对沪深300股指期货进行预测,结果显示：3种机器学习方法都有较好的预测能力,但XGboost的预测能力更优。

传统的线性建模方法仅仅是根据已有变量之间的关系来拟合,其结果通常与已有的设定值相差无几。神经网络等机器学习算法可以抓住特征之间的非线性关系,处理特征之间的多重共线性问题,在经济预测研究方面有突出的表现。与此同时,集成学习算法还有一个优势,可以对预测中各特征的重要性进行计算,从而反映出哪些因素驱动了预测结果。故通过集成学习方法,从理论上为GDP增长和其他宏观经济指标的预测提供了一个切实可行的分析工具。因此,本文建立了SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM集成模型,并采用麻雀搜索优化算法对模型的重要参数进行调整,并选取MSE、MAE、可决系数R2作为模型评价指标,通过对比分析选出对于国内生产总值增长率具有更好效果的预测模型。

1 相关算法原理

1.1 AdaBoost算法

AdaBoost是一种以Boosting算法为基础的迭代式学习算法,最早由Freund和Schapire提出[4]。此算法对Boosting技术的思想进行了很好的传承,即在每一轮的训练中,AdaBoost会增加被分类错误的样本的权重,从而在下一轮的训练中,弱学习器会更加专注于被分类错误的样本,从而提高分类准确率。当所有的弱学习器集都被训练完毕后,AdaBoost通过加权多数票的方式,将多个弱学习器集成为一个强学习器集。

1.2 RFR算法

RFR算法的基本思想是从一组Boot strap sampling随机样本中选择一组样本,利用CART模型对每一个样本进行模型化,再将多个决策树的预测结果进行结合,得出最后的预测结果。该方法是将多个决策树的预测值进行简化平均。可以使误差均匀化,并明显提高预测的准确性。

1.3 GBDT算法

GBDT算法(gradient boosting decision tree)也被称为梯度提升决策树,是一种由多个决策树组成的迭代算法,对AdaBoost算法进行优化和改进[5]。GBDT算法可以用于数据的分类和数据的回归。在使用GBDT算法进行回归预测时,先对输入的样本数据进行训练,然后每个决策树(较小的,即较浅的树深)被用来调整和修改预测结果。

1.4 SVR算法

支持向量机(SVM)是基于统计学习理论中的VC维度理论和经验风险最小化原理的一种机器学习方法。支持向量机回归(SVR)是在SVM的基础上发展起来的,用于解决回归预测问题。SVR继承了SVM良好的泛化能力和泛化力,在很多领域都有很好的表现。

1.5 XGBoost算法

XGBoost(eXtreme gradient boosting)是一种用于监督学习算法中分类和回归的极端梯度提升树算法,由Chen et al.[6-7]在2015年提出。由于GBDT的改进,XGBoost算法的运行速度比传统梯度算法至少快一个数量级,包括并行计算、近似树构建、内存优化和稀疏数据的有效处理。同时,CPU多线程加速了树的构建,支持多平台和分布式计算,并提供了出色的可扩展性,以进一步提高训练速度。

1.6 LightGBM算法

LightGBM(light weight gradient boosting machine)是一个常用于竞赛的模型,由微软在2017年首次开发[8]。它使用Boosting策略提升了模型,也是GBDT的改进算法。

1.7 SSA麻雀搜索算法

SSA的灵感来源于麻雀的觅食和反捕食行为[9]。该算法基于仿生学原理,即麻雀种群在日常觅食中有发现者、跟随者和侦察者3个主要角色。在目标优化问题中,拟合度的大小反映了每个麻雀位置所对应的可行方案的优势程度。更新麻雀位置的规则根据麻雀的适应度值而不同。

2 预测指标选取与处理

2.1 指标的选取及数据来源

本文通过参考相关文献[10-12],以宏观经济理论中凯恩斯ISLM模型为基本构造基础特征体系。凯恩斯ISLM模型构建基础特征体系从理论上来说,国民收入核算将GDP划分成四大类。

Y=C+I+G+NX

(1)

其中Y、C、I、G、NX分别代表国内生产总值、消费、投资、政府购买和净出口。

由此本文选取一般公共预算支出档期同比增长率(X1)、工业增加值月度同比增长率(X2)、第三产业增加值当期实际同比增速(X3)、出口额月度同比增长率(X4)、社会消费品零售总额月度实际同比增长率(X5)、居民消费价格指数(X6)、不变价国内生产总值GDP季度同比增长率(X7)共7个指标,数据期间为2003年第1季度至2022年第4季度。数据均来源于中经网统计数据库。

2.2 特征选择

在特征选择中,根据特征集与目标变量以及特征之间的相关性,从给定的特征集中删除一些特征,从而选择出相关的特征子集,该过程称为“特征选择”。

2.2.1 相关系数

在对指标进行相关分析时,最常用的一种方法是计算相关系数,它能够反映出变量之间的线性相关程度。其计算方法如下。

(2)

式中：cov(x,y)表示变量x和y之间的协方差,δx表示变量x的标准差,δy表示变量y的标准差。

ρx,y绝对值越大,说明相关性越强。其优点是计算简单,缺点是只能用来判断变量之间的线性相关程度,而无法描述变量间的非线性关系,即使它们之间的非线性关系很显著,相关系数仍可能接近0。

图1的热力图直观地展示了特征之间以及各特征与目标变量之间的相关系数,可以初步分析特征的重要性。图中显示,GDP(Y)与工业增加值(X2)的相关系数为0.96,与第三产业增加值(X3)的相关系数为0.95,二者之间的线性相关程度非常高,说明工业增加值与第三产业增加值是影响GDP的重要因素。

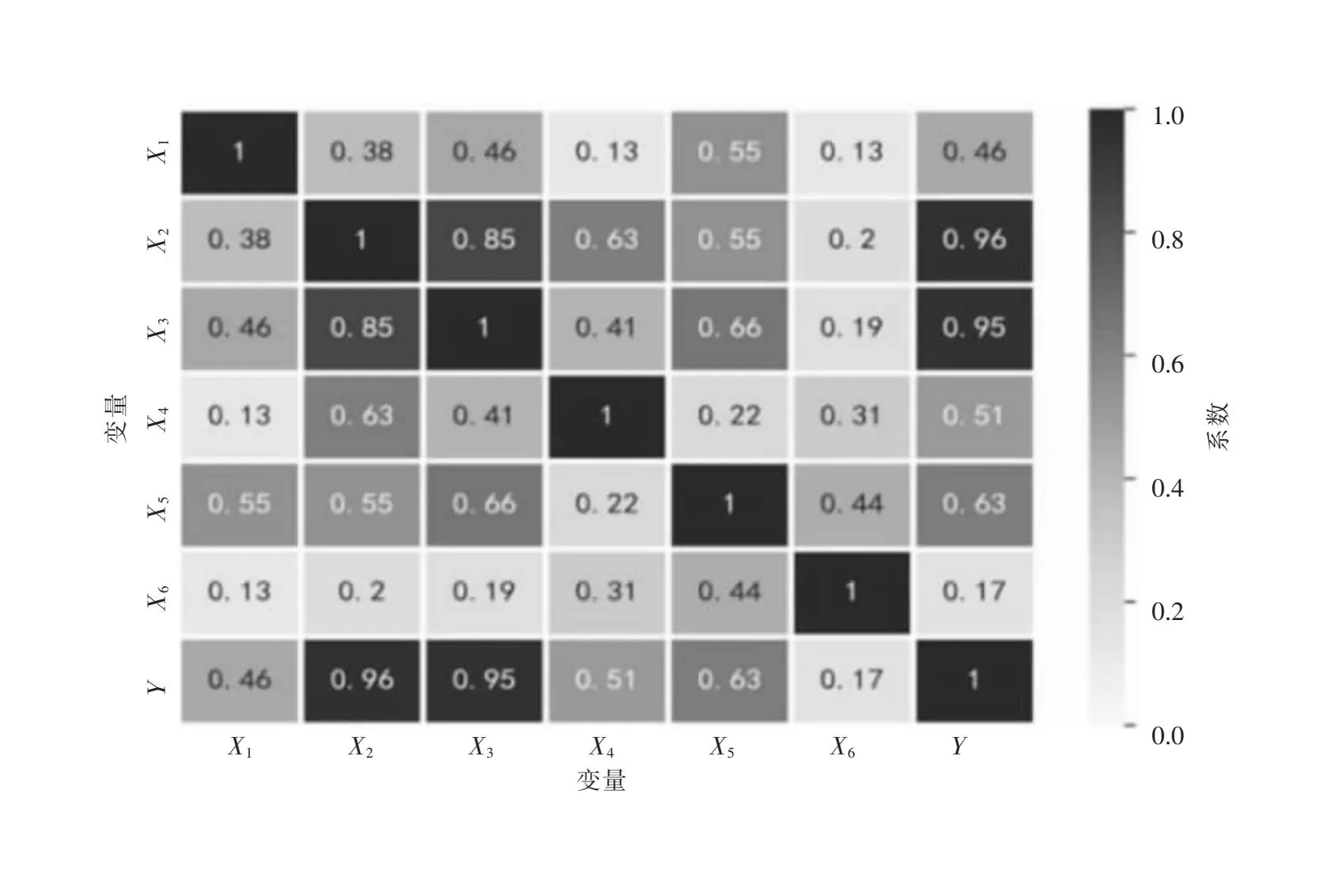
图1 相关系数热力图

2.2.2 互信息

互信息属于特征选择中过滤法方式的一种,它能够被用来对变量之间的线性关系进行描述,也能够对非线性关系进行描述,通常既可以用于回归也可以用于分类算法中。互信息的值越大,说明2个变量之间的相关性较强。随机变量x与y之间的互信息I(x,y)定义为：

(3)

式中：p(x)、p(y)与p(x,y)分别为随机变量x、y各自的边像概率分布和联合概率分布。

利用sklearn.feature_selection中mutual_info_regression函数可以得到各特征变量与目标量的互信息值,对数据集中的特征运用互信息过滤法筛选。观察可以发现,大多数互信息值大于0.1,因此,选取了互信息值大于0.1的特征,经过筛选后,最终所选取的特征按互信息值从大到小排序如图2所示。

图2 互信息值

由图2可知,互信息值小于0.1的变量有居民消费价格指数,因此,在构建模型时,为避免特征冗余的情况发生,选择将居民消费价格指数特征剔除,仅将其他剩余变量用于构建模型。

3 实证分析

3.1 数据准备与试验环境

由本文2.2.2所选取,一般公共预算支出、工业增加值、第三产业增加值、出口总额(美元)、社会消费品零售总额共5个指标作为预测模型的输入变量(影响因素),GDP作为预测指标。数据分析试验在Python 3.8环境下完成。

3.2 回归算法选取

本小节主要采用由Python程序语言设计的sklearn框架来构建SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM的预测模型。机器学习回归算法预测模型的构建大致流程为：特征工程—样本集拆分—回归算法选择—模型参数调优—模型验证与评估—模型预测。详细步骤描述如下。

1)使用经过预处理后的样本数据作为样本集,首先将样本集随机划分成8：2的比例,其中80%的样本数据作为训练样本集,20%作为测试样本集,利用pyhton编程语言包sklearn.model_selection中KFlod交叉验证法将样本集划分为训练集和测试集,模型的评估指标为MSE、MAE和R2。

2)使用缺失参数建立SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM算法模型。

3)利用麻雀搜索算法对每个预测模型进行相应的参数寻优,对预测模型进行优化。

4)在此基础上,对所提出的优化算法所修正的模型进行误差分析,并与所修正的模型进行比较,最终获得具有较好预测效果的机器学习回归算法。

3.3 麻雀搜索算法

在粒子群算法优化过程中,通过群体内个体的信息交换,整个群体的运动在解决问题的空间中产生了从无序到有序的进化过程,并由此得到一套参数最优解。在SSA中,每个麻雀对应的位置都可以成为优化问题的最优解。在目标优化问题中,拟合度的大小反映了每个麻雀位置所对应的可行方案的优势程度。更新麻雀位置的规则根据麻雀的适应度值而不同。最优模型对应的最优参数组合如表1所示。

表1 SSA算法最优参数取值

3.4 模型的优选

本文建立了SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM集成模型,并采用麻雀搜索优化算法对模型的重要参数进行调整,最终模型的预测效果以MSE、MAE和可决系数R2这3种评价指标来评估。

3.4.1 模型的评价标准

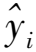
(4)

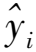
(5)

可决系数(R2)：用来衡量回归模型的拟合能力,R2值越接近于1,模型解释因变量的能力越强,即模型拟合效果越好。

(6)

3.4.2 模型优选结果

本文建立SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM集成模型引入麻雀搜索优化算法(SSA)对模型的重要参数进行调整后进行GDP增长率预测,各预测模型真实值与预测值对比如图3所示。

图3 6种预测模型真实值与预测值对比

由图3可知,经过麻雀搜索算法(SSA)参数优化后的6种模型中,SSA-GBDT模型和SSA-XGBoost模型相较于其他几种模型预测更准确,而SSA-LightGBM模型预测相对不准确。为更加清楚地看出各模型预测结果,计算各模型均方误差(MSE)、平均绝对误差(MAE)与可决系数R2,结果如表2所示。

表2 模型指标对比表

结果显示：对麻雀算法优化后的模型指标,依据模型预测性能的优劣情况将其按降序排列：SSA-GBDT、SSA-XGBoost、SSA-RFR、SSA-Adaboost、SSA-SVR、SSA-LightGBM。显然,与其他模型相比,SSA-GBDT模型具有更优的预测性能,MSE、MAE、R2分别为0.148 6、0.196 3、0.975 1。综上所述,基于麻雀搜索优化算法的GBDT模型预测性能显著优于其他模型,对于国内生产总值增长率预测具有更好的效果。

4 结束语

本文以探索季度GDP增长率变化的规律、寻求高精度预测季度GDP增长率的方法为目的,基于中经网统计数据库2003年第1季度至2022年第4季度的指标数据,分析我国GDP增长率预测模型。建立了SVR、GBDT、RFR、Adaboost、XGBoost和LightGBM集成模型,引入麻雀搜索优化算法(SSA)对模型的重要参数进行调整,以MSE、MAE、可决系数R2作为模型评价指标,比较多个模型的效果,选取具有更高预测精度的模型,能够更准确地预测GDP增长率。依据模型预测性能的优劣情况将其按降序排列为SSA-GBDT、SSA-XGBoost、SSA-RFR、SSA-Adaboost、SSA-SVR、SSA-LightGBM,其中,SSA-GBDT模型具有更优的预测性能,MSE、MAE、可决系数R2分别为0.148 6、0.196 3、0.975 1,说明基于麻雀搜索优化算法的GBDT模型预测对于国内生产总值增长率预测具有更好的效果。