不同含水率下级配碎石振动压实状态评价与机理研究
谢 康,李泰灃,肖宪普,3,陈晓斌,张千里,王业顺
(1.中国铁道科学研究院集团有限公司 铁道建筑研究所,北京 100081;2.中南大学 土木工程学院,湖南 长沙 410075;3.石家庄铁道大学 土木工程学院,河北 石家庄 050043)
高速铁路(以下简称“高铁”)路基长期承担轨道与列车反复作用,而路基结构静动变形控制标准达毫米级,对路基填筑质量与填筑效率提出了极高要求[1]。级配碎石作为高铁基床表层填料,具有高抗剪强度、低压缩性以及强抵抗变形的能力,进而可为高铁基床表层提供高质量、稳定的支撑基础[2-3]。
为确保级配碎石具备上述物理力学性质,需要对其填筑质量严格把控,主要包括级配和含水率两个方面[4]。大量高铁施工中,通过“厂拌”的模式保证级配碎石适用性[5],而对含水率的控制以“工人经验”为主[5-6],导致未处于最佳含水率的级配碎石在填筑中产生压实不均的问题,为此有必要探讨含水率对级配碎石压实干密度的影响。目前,最大干密度与含水率的关系主要通过室内击实[7]和振动台试验[6]进行研究,但缺乏级配与含水率方面的相关研究,同时击实试验难以完全满足现场实际情况[8],对级配与含水率的研究存在一定局限性。
铁路行业规定[6]砾石类最大干密度采用振动台振动加重物法,且同时要求采用干法或湿法开展试验。其中,湿法仅做了在烘干料中加适量水或用天然的湿土进行装样,并没有考虑含水量对干密度的影响,属于一种以经验为导向的方法。室内振动压实试验作为确定粗粒土最大干密度的方法之一[9-10],也是公认为与现场振动压实机理相同的试样成型方法[7],但是鲜有系统地涉及含水率对振动压实特性的研究。部分学者通过击实试验确定振动压实试验最优含水率,但二者之间压实机理存在差距,影响振动压实试验最优含水率的确定。针对高铁级配碎石振动压实特性的研究集中在物理指标(干密度)[11],然而,要全面评估其压实特性,除考虑干密度外,还需深入探究其力学指标(刚度和强度)。张家玲等[12]、王天亮等[8]采用物理力学指标表征填料的压实状态,同时指出对高铁填料这类复杂的混合材料,其性质与颗粒大小、形状和级配组成密切相关,干密度与力学特性之间的关系尚需具体研究确定。目前针对高铁路基级配碎石力学特性的研究,主要通过室内三轴试验进行研究。Seif等[13]通过一系列大三轴试验,比较分析了不同颗粒级配、含水率对级配碎石的抗剪强度的影响,类似地,Pham[14]通过大型静动三轴试验研究了级配碎石的强度和变形特性,分析了围压、细颗粒含量及含水率对其抗剪强度参数变化的影响。然而含水率对级配碎石振动压实力学性质影响的研究成果较少,难以表征出实际的压实状态。
振动压实试验中含水率对填料压实特性的影响鲜有研究,故有必要对振动压实下不同含水率级配碎石的压实状态开展深入分析。本文以不同土体结构类型的级配碎石为研究对象,采用室内振动压实和大型静三轴试验方法,提出将压实烘干后的临界含水率作为最优含水率,量化不同含水率下压密状态,深入探讨不同含水率下振动压实机理,研究成果可为高铁粗粒土填筑控制提供理论参考。
1 试验设计
1.1 试验材料
根据陈坚等[15]研究以及TB 10621—2014《高速铁路设计规范》[16]对级配的要求,选择如图1所示三种级配类型:骨架孔隙型R1、骨架密实R2和悬浮密实R3,以保证试验土样典型性[17-19]。

图1 试验级配碎石材料级配
1.2 试验设备
室内振动压实仪采用课题组研制的多参数可调式智能振动压实仪。为减少尺寸效应对填料最大干密度的影响,该设备有不同直径的压实筒,压实筒直径D=100、150、200、250、300 mm。高铁填料最大粒径dmax控制值为45 mm,且当径径比(D/dmax)大于4.7[20],尺寸效应对干密度的影响较小,故最终采用直径φ250、高h=250 mm压实筒成样。级配碎石强度特性试验采用大型静动三轴试验机,试验尺寸为φ300、h=600 mm。
为量化不同含水率对级配碎石压实过程的影响,需要形成干密度-压实时间曲线(压密曲线)。王萌等[7]在室内振动压实试验中,采用游标卡尺分别测试压实过程中不同阶段被压料的高度,进而计算出被压料干密度ρd为
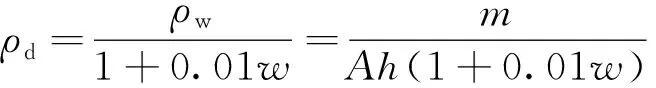
(1)
式中:ρw为填料湿密度;m为填料质量;h为填料厚度;w为填料含水率;A为压实筒底面积。
然而,这种做法不仅工作量大,花费大量人力,且易受人为因素干扰,存在较大误差。基于表面沉降理论,结合智能振动压实仪内置的沉降传感器,可在设备采集界面自动输出压密曲线。
压实中密度通过填料体积和质量求得,由于压实筒内填料的质量一定,只要测定体积的变化就可求出密度的变化,即初始密度ρ0为
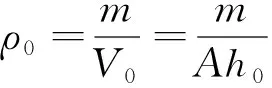
(2)
式中:V0为填料初始总体积;h0为填料厚度。
假设振动压实n次后沉降量为Sn,则n次振动压实后密度ρn为

(3)
式中:Vn为n次振动压实后体积;An为n次振动后填料的底面积;εn为沉降率。
设压实筒内填料总质量m不变,且振动压实前后面积不变,即
An=A
(4)
由式(2)~式(4)结合可得
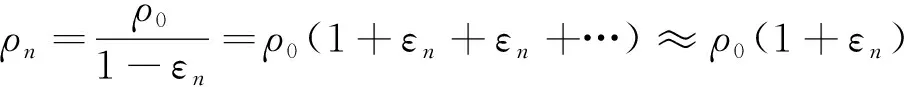
(5)
因此,如果ρ0已知,只需测量Sn,则可计算出n次振动压实后填料ρn。因此,在试验中,只需测试装样后ρ0,其他情况下测出沉降量即可计算出对应的密度,最终取压实稳定后的干密度作为最大干密度ρdmax。
1.3 试验方法
振动压实试样制备时,采用四分法分别称取3种级配的样品,振动压实试样中分别选取含水率w =0%、2%、4%、5%、6%制样,每组试样平行制样3组,总共45组进行振动压实试验。采用花洒方式将水与级配碎石均匀拌合,然后静置一夜,以保证粗细颗粒充分湿润。
为使室内振动压实试验与现场碾压的效果一致,试验中控制室内压实功与现场压实功一致。刘东海等[21]通过调整室内振动次数,以保证试验与现场碾压压实功一致。根据振动理论,碾轮(夯头)的振动荷载幅值P为
P=m+Fsinωt
(6)
式中:F为碾轮产生的激振力;t为振动时间;ω为碾轮振动频率。
由于土体阻尼的存在,致使碾轮垂直位移与激振力之间产生相位差φ,此时得到碾轮单位周期压实能量为
当碾轮振动频率与土体固有频率相同时,相位差为90°,级配碎石振动压实的最优频率在30Hz左右,故在现场碾压振动频率可选取为30Hz。此时,可将压实能量E简化为
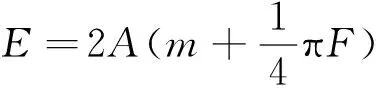
(8)
碾轮和铁夯头振压n遍后所做的单位体积压实功E0-1、E0-2分别为
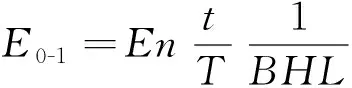
(9)
式中:n′为夯头振动次数。
将式(8)代入式(9)、式(10)可得
式中:B为振动轮宽度;H为碾压层厚度;v为压路机行走速度;m′为夯头压实下填料质量;F′为夯头产生的激振力。
基于广湛高铁新兴段现场实测结果,基床表层围压一般为15~60kPa,故选取15、30、60kPa共三种工况进行不同含水率的静三轴试验。加载中采取固结排水剪切,按分级加载方式进行加载,最后采用位移法,以0.3%/min(1.8 mm/min)的应变速率进行加载,当主应力差与轴向应变表现为下降时停止加载。
2 不同含水率级配碎石压密特性分析
2.1 干密度分析
R1、R2、R3试样不同含水率下试样干密度变化见图2。另外,增加R2在击实试验中的最优含水率,比较两种压实方式下含水率对干密度的影响差异。
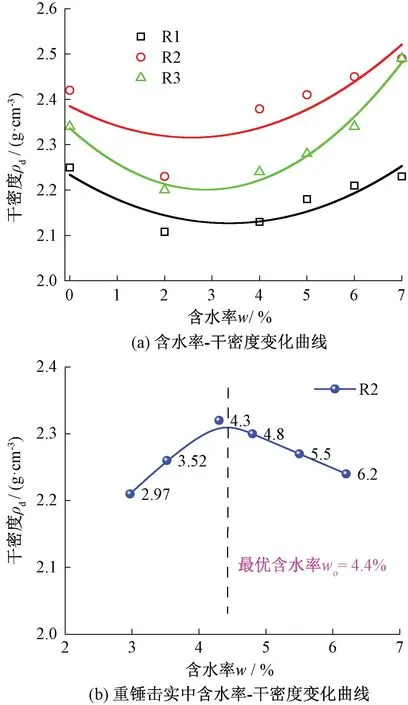
图2 不同含水率下试样干密度变化
如由图2可知,振动压实试验中三种级配填料的最大干密度均随含水率增加呈现“缓慢减小—缓慢增加”的趋势;而R2填料在击实试验中最大干密度随着含水率增加呈现“缓慢增加—缓慢减小”的趋势,存在最优含水率wo=4.4%使试样干密度最大为2.32 g/cm3。
由图2(b)可知,当振动压实试验中R2的最优含水率为4.4%时,试样存在“冒浆”和“起皮”现象。这个现象与陈祖正[22]将铁路粗粒土填料试样含水率设定为5%时的现象类似,且当含水率大于4.4%时,干密度仍逐渐增大,这与击实试验结果不符,该结论与吴龙梁[23]振动压实试验结果一致。
压实前后含水率变化见图3。由图3可知,振动压实前后含水率变化受压实前含水率影响较大,当压实前含水率较低时,压实前后的填料含水率基本不变;而当含水率较大时,“翻浆”导致部分水流失,压实后含水率变化呈减小趋势,但压实后含水率趋于稳定。因此,可将“翻浆”试样压实后的烘干含水率作为临界含水率wv。

图3 压实前后含水率变化
振动压实试验中R1、R2、R3的含水率为临界含水率(3.5%、4.0%、5.4%)时,试验过程中未产生“翻浆”,且其干密度分别为2.14、2.42、2.35 g/cm3。以R2为例,击实试验和现场振动压实中的最大干密度分别为2.32、2.38 g/cm3,通过击实试验最大干密度确定压实度K> 1.0,而通过振动压实试验最大干密度和临界含水率确定压实度为0.983,满足高铁路基填筑质量要求。
2.2 振动压密特性分析
基于所获得的压密曲线,采用压密曲线的密实能量指标来反映级配碎石的密实内在信息[23],见图4。

图4 压密曲线
为研究级配碎石在振动压实过程中的压实特性,根据现有研究成果[24],提出密实能量CEI和工后沉降能量TDI两个指标表征级配碎石在压实阶段的压实性能。碾压期的密实能量指数CEI表示级配碎石在填筑中,压实到一定的密实度时,压实设备所做的功。如果级配碎石压实度接近100%,级配碎石会产生塑性破坏,导致线路过大沉降。故将级配碎石压实度从95%~98%围成的曲线面积定义为TDI。TDI越高,则意味着级配碎石达到破坏时,需要更大的列车荷载,基床越稳定。大量试验经验发现,压密曲线符合对数曲线生长趋势,即在压实初期增长迅速,但随后进展就越发困难,最后保持稳定。CEI和TDI两个指标的计算式为
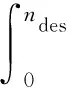
(alnn+b)dn
(13)
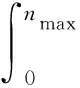
(alnn+b)dn
(14)
式中:a、b为拟合参数;ndes为K=96%时的振动次数;nmax为K=98%时的振动次数。
不同含水率下压实参数曲线见图5。对于相同级配的试样,增加一定量含水率后,CEI才会减小,使得其消耗的压实能量低,主要原因是水在级配碎石颗粒间主要起着润滑的作用。当含水率超过有效含水量后,CEI逐渐趋于稳定,说明水膜达到一定厚度后,增加含水率对压实性的改善效果有限。在含水率较低时,相同含水状态下的级配碎石,细级配大于粗级配,说明相同含水状态下细级配较难压实,主要原因在细级配对水的反应敏感,因水的表面张力作用,使得土料颗粒相互紧靠,阻止其移动,压实效果稍差。TDI随着细颗粒含量增加减小,说明细级配的抗变形比粗级配差。但充分洒水后,土料颗粒表面张力消失,使得细级配压实效果又变得良好。同时,细级配的抗变形在压实过程中均小于粗级配,主要原因在于粗级配更容易形成稳定的骨架。
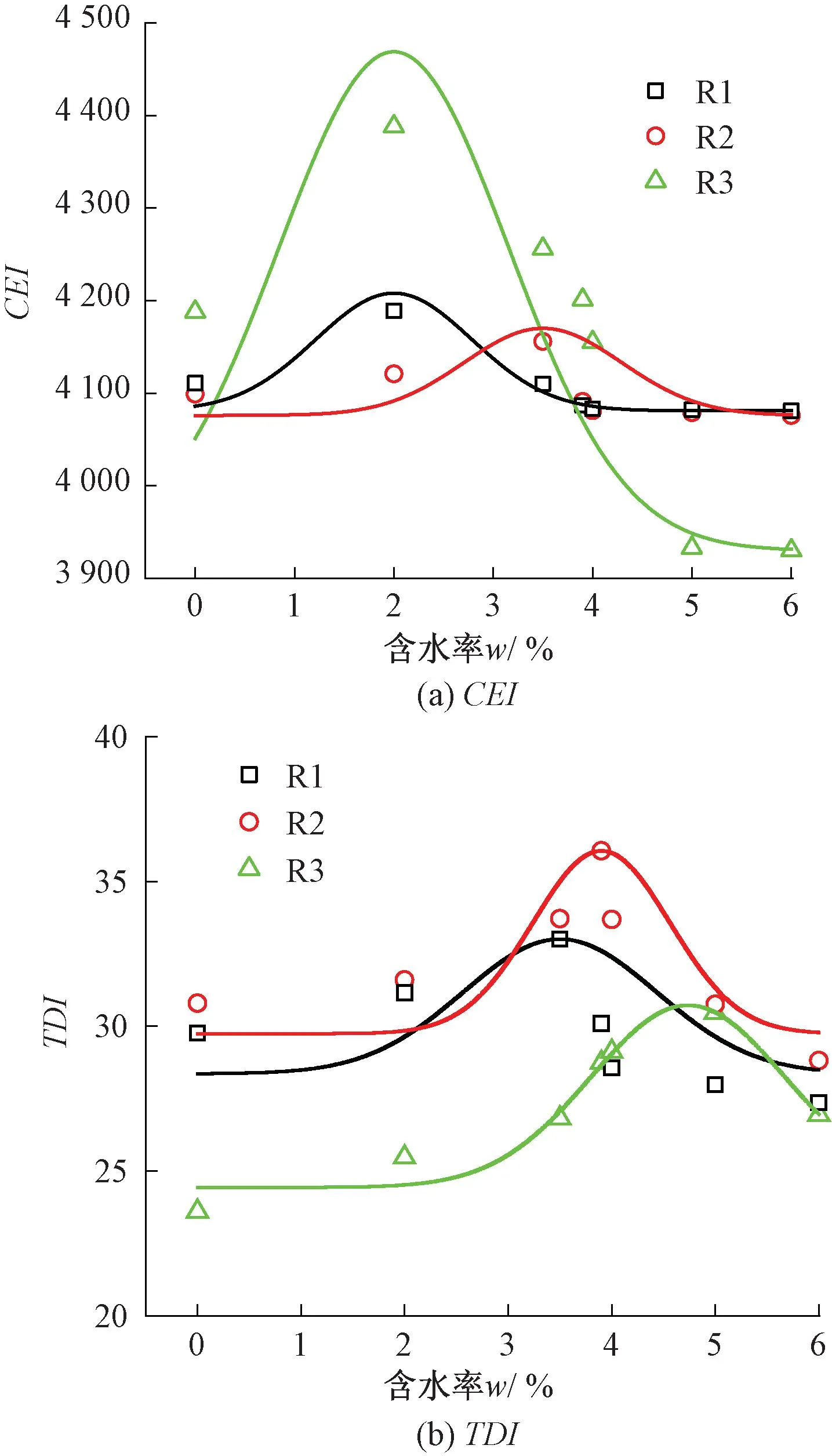
图5 不同含水率下压实参数曲线
2.3 振动压实下破碎特性分析
在振动压实中,激振力会导致级配碎石颗粒的棱角磨损,使得试样级配变异[25]。将振动压实后的各组试样进行烘干、筛析比较前后颗粒级配累积曲线,见图6。
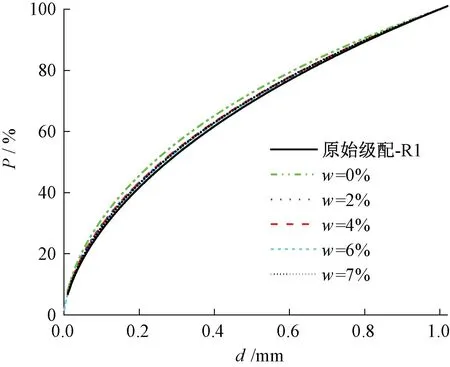
图6 不同含水率下R1压实前后级配曲线
由图6可知,随着含水率增加,振动压实前后各粒径筛孔的通过率皆呈先减小后增加的趋势。当含水率较低时,颗粒间发生相对运动时,缺少水的缓冲和润滑作用,颗粒破碎较为明显,尤其是填料处于干燥状态下,振动压实成型之后的级配发生较大变异。
为定量表征不同含水状态级配碎石振动压实前后颗粒破碎特性,采用相对破碎率Br来量化颗粒破碎程度,计算方法为
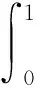
(16)
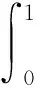
(17)
式中:bp为该粒径破碎的潜在能力;bp0、bp1分别为压实前后的bp值;f为级配曲线方程;Bp、Bt分别为压实前颗粒潜在的破碎能力和压实后发生的颗粒破碎量。
相对破碎计算结果见表1。
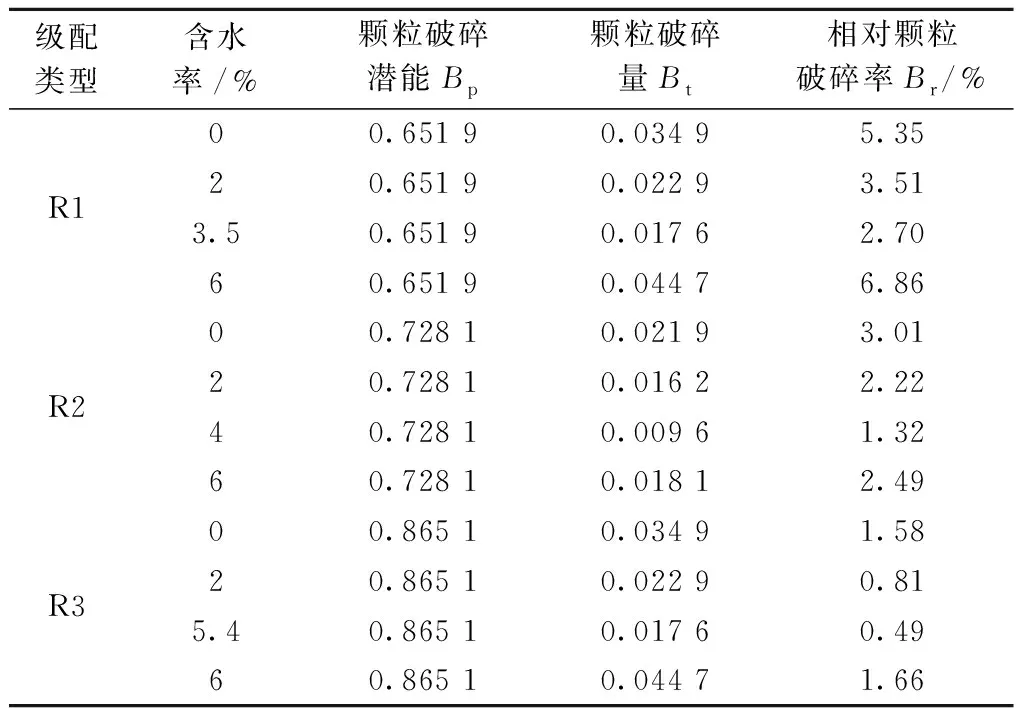
表1 相对破碎分析
由表1可知,随着试样中粗颗粒含量增多,颗粒的相对破碎率增大。R3中细颗粒含量较多,级配在振动压实前后基本不变;各组级配中相对破碎率均随着含水率的增加而先减小后增大,若试样中含水率较低时,尤其是大颗粒含量多的试样在压实过程中形成的土体颗粒结构较为单一,部分土颗粒骨架出现应力集中,导致更多的颗粒破碎;当含水率处于临界含水率时,水对颗粒间润滑、缓冲效应更加明显,破碎更不显著;但随着含水率进一步增加,部分细颗粒被水带出,产生翻浆现象,试样进一步被压缩,导致大颗粒之间互相接触,破碎率增大,故细颗粒含量较少的R1在高含水率会发生较大破碎现象。
3 不同含水率下级配碎石刚度和强度特性分析
对于粗粒土这类复杂混合材料,其性质与颗粒级配以及外部环境等密切相关,密度、刚度以及强度的变化仍需具体情况具体分析,故需要对不同含水率下级配碎石刚度和强度进行深入分析。
3.1 刚度分析
国内外提出的连续压实控制CCC[26]均是通过在振动设备上安装相应的加速度传感器,实时检测分析振动压实中填料的压实状况。马丽英等[25]建立路基振动压实系统动力学模型,验证了振动加速度反映结构刚度的正确性。结合振动压实设备激振头上所安装的三向加速度传感器,通过DH5922D采集振动压实系统的加速度信号曲线,表征出不同含水率下刚度变化。
对加速度信号经过滤波、消除多项式趋势、平滑等预处理后,计算振动稳态后的加速度幅值,见图7。

图7 不同含水率下加速度幅值对比
不同含水率下,R1、R2、R3的加速度峰值均呈现出先增大而后减小的趋势,且都在各自临界含水率附近达到加速度幅值最大值,振动响应越剧烈,颗粒运动趋势更显著,进而形成更加稳定的结构。试验中还发现粗颗粒为主的R1加速度峰值最大,而细颗粒为主的R3加速度峰值最小,可见粗颗粒为主的填料,刚度明显增大。
3.2 强度分析
采用三轴剪切试验分别分析R2不同含水率(w1=2%、w2=4%、w3=6%)下级配碎石的静强度的变化。不同围压下试样的应力-应变关系曲线见图8。
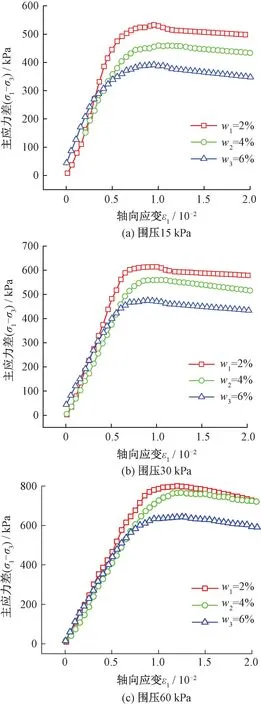
图8 不同含水率下R2强度曲线
由图8可知,不同的含水率的级配碎石试样的应力-应变曲线均为应变软化型,具有显著的峰值强度,随着围压的增大抗剪强度逐渐提高;应力-应变曲线随应变的增大表现为线性向非线性的转变。破坏应变随着含水率增大而稍微变化:当围压为15 kPa时,w1、w2和w3试样破坏应变分别为0.95%、1.00%和0.95%;当围压为30 kPa时,w1、w2和w3试样破坏应变分别为1.00%、1.05%和0.90%;当围压为60 kPa时,w1、w2和w3试样破坏应变分别为1.20%、1.25%和1.25%。
分别计算出各含水率下黏聚力和内摩擦角,w1的黏聚力Cd=81.5kPa,内摩擦角φd=49.3°;w2的黏聚力Cd=66.2kPa,内摩擦角φd=48.1°;w3的黏聚力Cd=59.2kPa,内摩擦角φd=47.5°。由以上分析可知,试样黏聚力随含水率的增大而减小,而内摩擦角基本保持不变,反映出级配碎石的摩擦角对含水率的变化不敏感,不同含水率下级配碎石试样抗剪强度的衰减主要由黏聚力降低引起。由此可见,在振动压实中,保持级配碎石内部含水率在临界含水率附近,成型试样的强度最大,多余的孔隙水会减少颗粒间的黏聚力,导致强度减低。
4 含水状态对振动压实机理讨论
级配碎石振动压实是一个复杂的物理过程,颗粒会互相嵌锁在一起,形成不同“堵塞”状态(jammed state)[26]。该“堵塞”状态表示在静态作用下,级配碎石内部颗粒难以进一步移动,只有继续增加振动剪切力的作用,内部颗粒才可以移动,使得级配碎石体积改变。然而在不同含水率下,级配碎石在振动后所形成的“堵塞”状态的物理力学不同,随着填料含水率增加,不同“堵塞”状态的物理力学演化形象表达见图9。
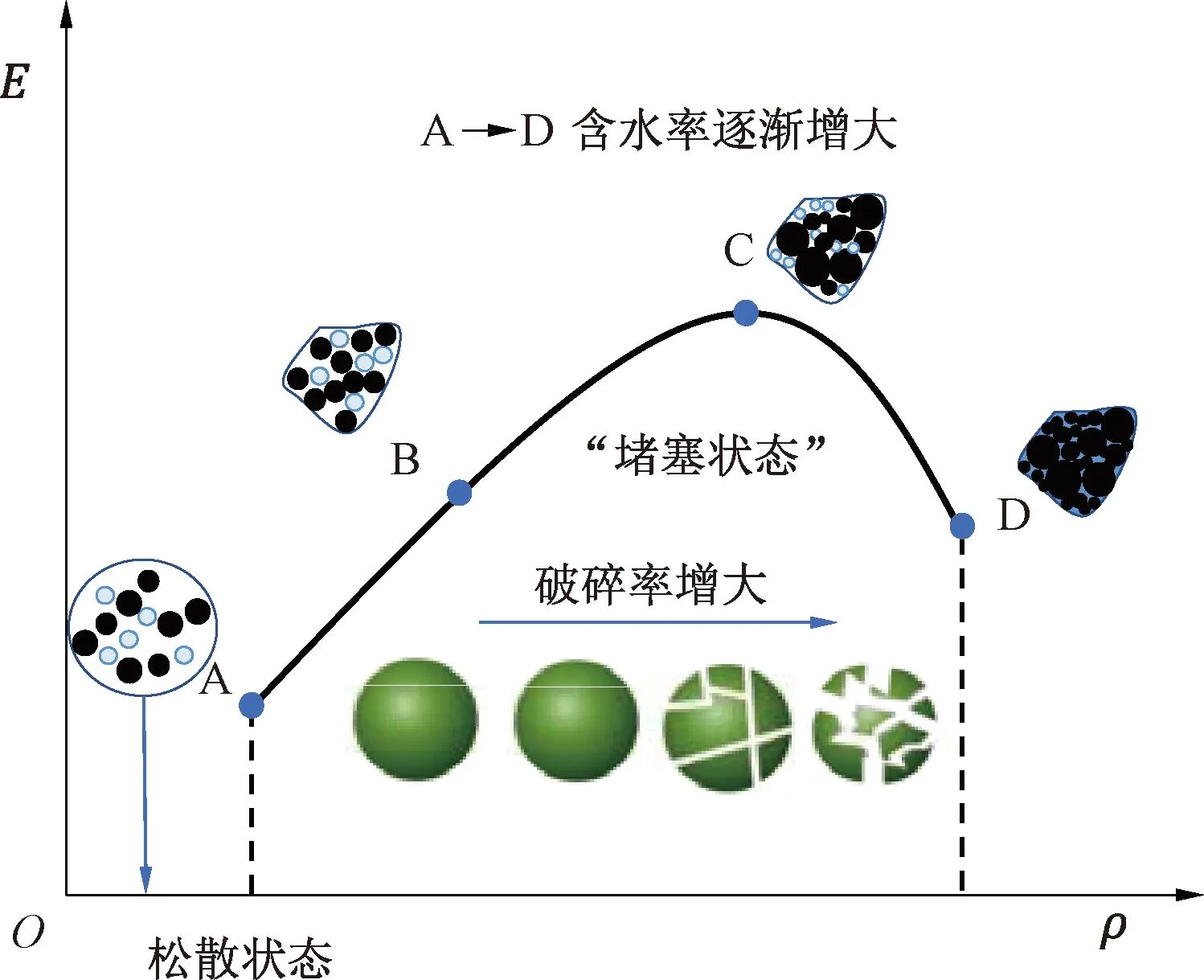
图9 不同含水状态(w>0)下压实状态演化机制示意
假设图9中各状态下均通过相同的振动压实能成样,节点A→B→C→D表示含水率逐渐增多的过程。A→B→C过程中,随着含水率的增加,填料颗粒处于“堵塞状态”,小颗粒填充大颗粒间孔隙,使得孔隙减小,试样逐渐密实。此过程的强度、刚度均随着干密度的增大而增加。然而,当含水率增大至wv时,此时刚度和强度也达到最大值,进一步增加含水率,颗粒破碎增大,填料干密度增大,但是填料刚度和强度下降,所形成的路基填筑状态发生劣化。
为解释颗粒间含水状态对强度的影响,应用土力学临界状态孔隙水压力和有效应力的理论,即
p=pe+pp
(19)
式中:p为土体总应力;pe为土体有效应力;pp为孔隙水压力。
在压实过程中,p固定不变,随着pp的增加,导致pe减小。填料成型后的强度变形与填料内部颗粒之间的摩擦密切相关,而颗粒之间的摩擦与pe正相关。振动压实过程中,随着试样体积减小,颗粒互相接触,孔隙减小,pe逐渐增大,如果含水率较低,水仍可以在孔隙中自由流动,但是当含水率增大一定程度后,pp进一步增大,而外界总应力保持不变,故pe减小,导致成型后填料强度下降。同时,颗粒破碎程度增加,土体骨架强度也下降,可运动的细颗粒逐渐增多,使得pe进一步减小。
5 结论
为探讨振动压实下级配碎石的含水率效应对压实状态的影响程度和机制,以不同土体结构类型的级配碎石为研究对象,采用室内振动压实和大型静三轴试验方法,提出了临界含水率wv作为振动压实法的含水率方法,量化不同含水率下压密状态,揭示了不同含水率下振动压实机理,研究成果可有助于深入解释振动压实机理,为高铁粗粒土填筑控制提供理论参考。结果表明:
1)将击实试验最优含水率作为振动压实含水率,试样在压实过程中产生“翻浆”,而振动压实含水率为临界含水率时,未产生翻浆现象,且满足现场碾压标准。
2)水在级配碎石中主要起到润滑和缓冲作用,临界含水率可以保证CEI和TDI处于最佳状态,且颗粒破碎最低。
3)级配碎石内部含水率在wv附近,成型试样的刚度、强度最大,多余的孔隙水会减少颗粒间的黏聚力,导致刚度、强度减低。
4)采用临界状态孔隙水压力和有效应力的理论,解释颗粒间含水状态对填料振动压实的影响,即当含水率超过wv后,在外界总应力保持不变的情况下,pp增大,pe减小,导致成型后填料强度下降。

