基于超宽带定位的室外定位系统设计

李 斌，周帅宇，陈 洁，袁 浩

（上海大学 机电工程与自动化学院，上海 200444）

近年来，随着体育产业的快速发展，我国运动员在国际赛场上与其他国家高水平运动员相互博弈的过程中，逐渐意识到科学的训练方式和精密的训练分析手段的重要性。尤其在田径项目中运动员的步态、速度、动作等都极大地影响着最终的比赛成绩，所以如果能实现对运动员的精确定位，就能帮助运动员和教练通过分析定位数据有针对性地安排训练任务，提高训练效率，有效提高最终的比赛成绩。

超宽带（ultra-wideband，UWB）技术是一种新型的无线通信技术，美国联邦通信委员会规定了相对带宽不小于20%或者绝对带宽不小于500 MHz 的信号属于UWB 的范畴[1]，由于UWB 的穿透能力强、抗多径效应能力强和成本低等特点，目前多用于高精度定位。目前UWB 定位技术一般用于室内范围的精确定位，室外定位一般使用GPS 定位[2]。对于本文的应用场景—田径运动的人体定位，要求高刷新率、高精度，GPS 显然达不到这样的要求。所以本文设计了一套基于UWB 定位的室外定位系统，该系统能在室外达到对人体的高刷新率、高精度的定位要求。

1 UWB 定位算法设计

1.1 UWB 测距方法选择

UWB 本质上是一种电磁波信号，它以光速在空气中传播，使用2 个支持UWB 的设备即可完成测距，具体过程是使用一个发射机A 发射UWB 信号，另一个设备B 作为接收机接收UWB 信号，发射机A 和接收机B 分别记录发送或接收的时间，根据2个时间差即可得到UWB 信号在空间中传播的时间，根据该时间与电磁波传播速度的乘积即可得到2 个设备之间的距离[3]。

这种单边测距（one-way ranging，OWR）的方法需要发送和接收设备的时间同步，对设备的时钟同步性要求很高。使用双向测距算法（two-way ranging，TWR）可以减小由于定位系统时间不同步所导致的误差。双向测距算法包含单边双向测距算法（single sided two-way ranging，SS-TWR）和双向双边测距算法（double sided two-way，DS-TWR）等[4]。

单边双向测距算法是在单向测距的基础上改进的，增加了一次B 向A 发送的流程，如图1 为单边双向测距算法的原理图。

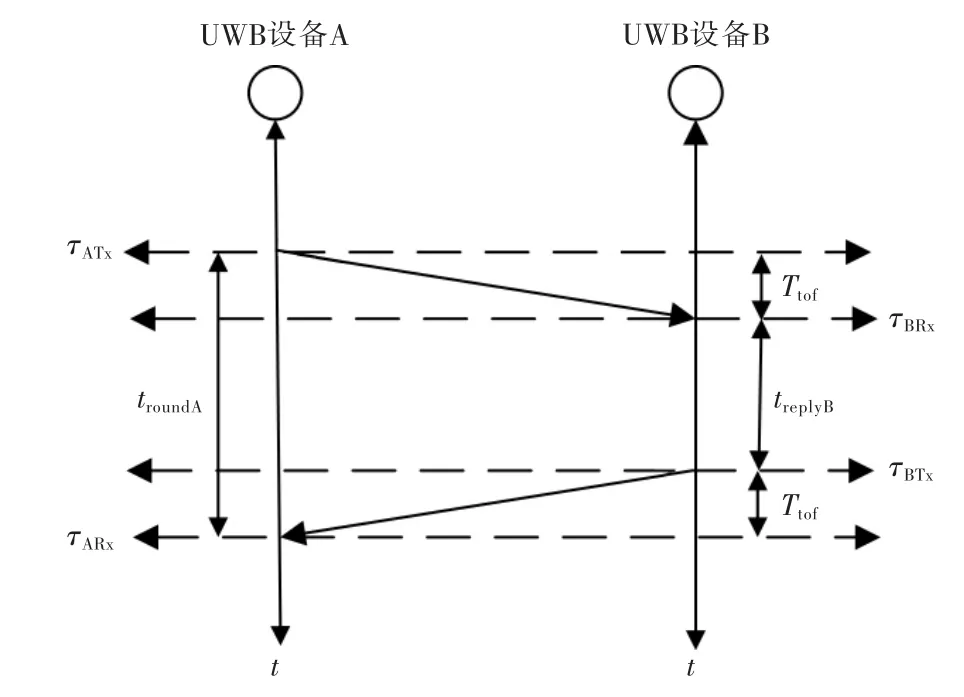
图1 单边双向测距算法原理图Fig.1 Schematic diagram of single sided two way ranging algorithm

A 在时间戳τATx发送信号，B 在时 间戳τBRx时收到A 的信号后，在短暂延时后向设备A 发送信号，记录此时的时间戳τBTx，A 收到信号时记录时间戳τARx，此时A 和B 设备中分别记录了发送和接收的时间戳，可以由此计算B 设备在收到信号到发送信号的延时为

从测距开始到结束的时间为

由测距总时间troundA和发送延时时间treplyB可以得到UWB 信号的单次飞行时间（time of fly，TOF）为

得到Ttof即可计算出设备A 和设备B 的距离。

双边双向测距在单边双向测距的基础上，又增加了一次向B 设备发送信号的过程，可以减小时钟漂移对延迟精度的影响，但同时增加了每次测距的时间[5]。为增加测距的刷新率，本系统选择单边双向测距。

1.2 UWB 定位原理

在无线定位技术中，通常将已知空间位置的设备称为基站，将待定位设备称为标签。由几何知识可知最少需要3 个圆可以确定平面上的1 个点，最少需要4 个球可以确定空间中的1 个点。因此对于二维空间定位，需要3 个基站确定1 个标签的位置。由于测距过程中存在误差，所以对于基于到达时间或者双向测距的测距方法获取到的测距信息，可以使用最小二乘法估算UWB 设备的位置信息[6]。以二维定位为例，如图2 所示Bi（i＝1，2，3）分别为3 个位置信息已知的UWB 设备，即基站，将3 个基站的坐标记为（xi，yi）（i＝1，2，3），L 为需要定位的UWB 设备，即标签，将标签的坐标记为（x，y）。

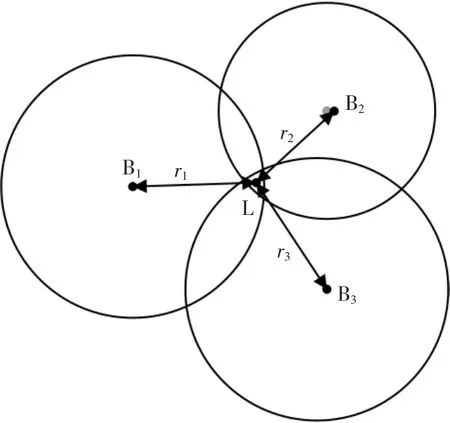
图2 最小二乘法定位示意图Fig.2 Schematic diagram of the least squares method for positioning

由测距算法得到的基站与标签的距离分别为ri（i=1，2，3），则可以列出以下方程组：

将2 个等式分别与第三个等式做差可以得到：

其中A、X、b分别为

由于测距过程中存在误差，误差可以表示为

为了使得误差最小，令f（X）＝（b-AX）T（b-AX），则X=argmin f（X），解得：

至此求得标签的估计位置。

2 定位精度评价指标

常用的定位精度有均方根误差、累计分布函数、平均误差、克拉美罗下界等标准[7]。本文主要使用均方根误差作为评价标准。

均方误差（mean squared error，MSE）是指测量值与真实值之差的平方的数学期望值，如式（11）所示：

均方根误差（root mean square error，RMSE）是均方误差的算数平方根，如式（12）所示：

3 硬件设计

3.1 DW1000 模块

DW1000 模块是DecaWave 公司的一款符合IEEE超宽带标准的无线收发模块。它由DW1000 芯片、天线、平衡-不平衡电路和晶振电路组成，它可以实现高速的数据传输，精确记录发送与接收时间的时间戳，使用SPI 通信方式将UWB 通信数据发送给主控芯片[8]。除此之外，DW1000 模块封装面积小，方便应用于可携带设备上，因此选择DW1000 模块作为设备的UWB 通信模块。

3.2 蓝牙模块

HC-05 模块是一款高性能的主从一体化蓝牙串口模块，可以通过指令设置波特率与工作模式，使用和调试简单方便，适合短距离的数据传输。UWB设备在完成一轮测距后需要将测距信息发送给上位机计算定位信息，本系统使用HC-05 蓝牙模块完成测距信息的发送与接收，图3 所示为蓝牙模块的通信示意图。

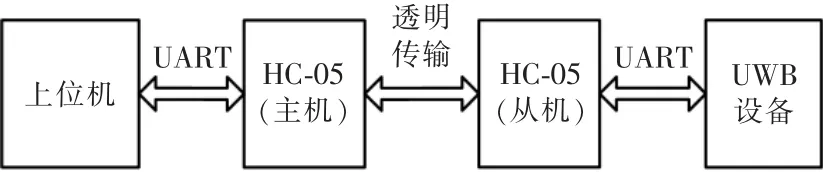
图3 蓝牙模块通信示意图Fig.3 Bluetooth module communication diagram

3.3 STM32 模块

STM32F103C8T6 是ST 公司推出的基于Cortex-M3 内核的32 位微控制器，包含多个定时器，外部时钟最高倍频可达72 MHz，支持USART、SPI、CAN等多种通信方式，本系统的UWB 硬件设备使用STM32-F103C8T6 作为主控芯片。如图4 为基于STM32F103-C8T6 的系统结构图。主控芯片使用SPI 方式与DW1000 进行通信，获取时间戳、队列号等信息，通过串口将计算出的距离信息发送给蓝牙模块，蓝牙模块将信息发送给上位机。

图4 系统结构图Fig.4 System structure diagram

4 实验验证

在前文已经介绍了该系统的测距与定位算法以及硬件设计。本节对定位系统进行验证，分别测试测距精度与二维空间的定位精度。

4.1 测距实验

为了后续分析定位算法的估计效果，需要先对测距精度进行验证，首先设置2 个UWB 设备的DW1000 的关键参数一致，包括UWB 信道、脉冲重复频率、数据速率测距频率等[9]，如表1 所示。

表1 DW1000 关键参数设置Tab.1 DW1000 key parameter settings

其中前导码是信号结构的重要部分，其主要目的是帮助接收器进行时间和频率同步，以及无线信道估计。脉冲重复频率是发射脉冲或脉冲组的速率[10]。

本次测距实验使用2 个UWB 设备和1 对蓝牙模块，实验场地选择空旷的室外环境，使用2 个支架分别固定2 个UWB 设备，调整支架高度使得2个UWB 设备的天线高度一致，保持一个UWB 设备的位置不变，沿着一条直线移动另一个UWB 设备的位置，每次移动1 m，每次移动位置后记录测距信息，实验记录了1～9 m 的测距数据。取每次测距的1000 个数据进行分析，如图5 所示分别为3 m、5 m、7 m 的测距数据。

图5 测距数据Fig.5 Ranging data

由图5 可以看出，UWB 测距数据在均方根误差上下浮动，且均方根误差与实际距离存在差值，可知UWB 测距数据存在随机误差和系统误差，随机误差可能受DW1000 的时钟漂移影响，DW1000 的外部晶振可能由于环境温度和工艺差异等因素的影响导致UWB 设备的时钟频率有些许不同，微小的时钟漂移会给测距结果带来较大的误差[11]，系统误差受到天线延时影响。除此之外，随着距离的增加，异常数据逐渐增加，这是由于在数据传输速率较高时，UWB 信号衰减较大，可能会达不到接收器的识别信号的阈值[12]。

绘制1～9 m 的均方根误差和平均误差随距离变化的关系图，如图6 所示。

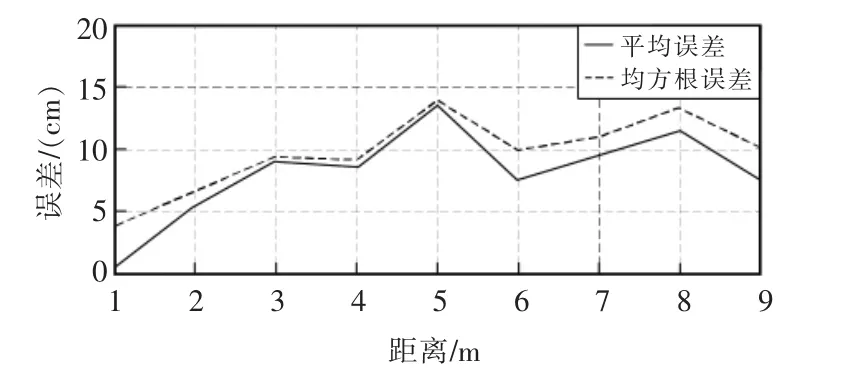
图6 误差随距离变化关系图Fig.6 Relationship between error and distance variation

由图6 可知，均方根误差和平均误差都在14 cm以下，且随距离增加的增加而增大，符合SS-TWR 算法的误差规律。

4.2 定位实验

在完成测距实验之后进行定位实验，4 个UWB设备的DW1000 的参数设置与测距实验时一致。使用4 个支架固定4 个UWB 设备，调整支架高度使4个设备的天线高度一致，放置在室外空旷环境。其中3 个设备的位置固定，组成一个等边三角形，作为基站，记为B1，B2，B3，1 个UWB 设备作为标签在B1、B3 连线所在边的高上移动，作为标签，记为L。实验场景的俯视示意图如图7 所示，以B3 为原点，以B3 向B2 方向作为x 轴正方向，以L 移动方向作为y 轴方向建立参考坐标系。

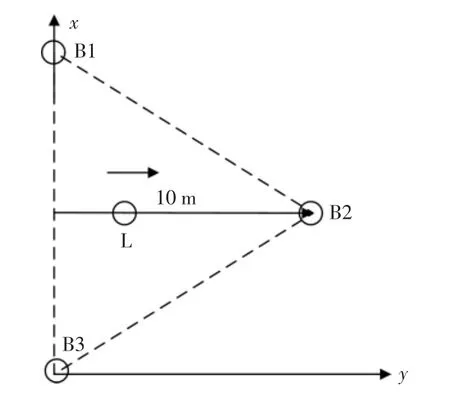
图7 定位实验场景示意图Fig.7 Schematic diagram depic ting of experimental scenario for localization

该高的长度为10 m，从底边与高的交点作为起点，标签每次移动1 m，每次移动记录定位信息，每次记录1000 个位置数据，由于UWB 设备在数据通信速率较高的情况下通信距离较短，因此实验记录从0～6 m 的定位数据，如图8 所示，三角形表示实际位置，圆圈代表定位算法估计的位置。

图8 定位实验结果图Fig.8 Graphical representation of the experimental results for localization

由图8 可知，定位数据存在随机误差与系统误差，估计位置与实际位置较为接近，计算0～6 m 的均方根误差如表2 所示。

表2 定位均方根误差Tab.2 Root mean square error（RMSE）for localization

由表2 可知0～6 m 内的定位均方根误差最大为15.8 cm，最小为8.52 cm，对于一般的田径运动能够满足室外定位的要求。

5 结语

本文介绍了基于UWB 定位的室外定位系统的设计，包括测距算法、定位算法、硬件电路的设计，目的是应用于小型体育场地的人体精准、高刷新率定位场景。其中使用SSTWR 的测距算法实现了高刷新率的要求，使用最小二乘法定位算法实现了定位误差的最小化。最后对本系统的测距精度进行实验，经过分析可知，最大误差不超过14 cm。对定位精度进行实验，在二维定位情况下，定位的均方根误差不超过16 cm。综上，该系统可以满足一般小型场地的田径运动人体定位。