冻结重塑黏土分数阶蠕变本构模型分析
姚兆明,蹇膨远,孔宏水,李 南
(1.安徽理工大学 土木建筑学院,安徽 淮南 232001; 2.矿山地下工程教育部工程研究中心,安徽 淮南 232001)
冻土强度是其最重要的力学指标之一,也是冻土工程领域最重要的研究课题之一[1]。自二十世纪二三十年代苏联科学家率先对冻土的各种性质进行研究,并逐步建立起冻土的强度理论和蠕变理论。研究发现,土体在负温条件下的强度值远大于自然状态下的强度值,且土体所处的环境温度越低,抗压强度越大。主要原因是土体中未冻水随着温度的降低冻结成冰,使土体本身内部的冰含量增加,冰的强度远大于水的强度,且冰的胶结作用增强了土壤颗粒之间的摩擦力和黏聚力,进而使冻土的强度提高[2-3]。学者开展了大量的室内外冻土强度组成性质试验研究,Goughnour等[4]研究发现,多数情况下冻土强度大于其自然状态下的强度与冰的强度之和,土体干重度的增大也会增大冻土强度。Ting等[5]对负温环境下的砂土开展单轴压缩试验,从土壤颗粒强度、冰的强度及结构三方面分析冻土的影响机理与强度组成。冻土的蠕变特性是冻土在施加恒定加载应力后,应变随着时间的变化增大,直至土体本身失去稳定最终达到破坏的过程[6]。学者通过构建诸多蠕变模型来模拟冻土的蠕变行为,可分为经验模型、流变模型和黏弹塑性模型等三类。曹虎生等[7]在开尔文模型的基础上进行改进,并对优化后的参数与温度线性回归,得到了考虑温度的冻土蠕变模型。姚兆明等[8]建立了考虑温度效应的冻结黏土内变量蠕变模型,利用智能算法对模型参数进行计算和修正,并用不同加载等级的蠕变试验对模型进行验证,结果表明该模型可较好地模拟冻土蠕变行为。
上述模型均为整数阶蠕变模型,其对于岩土蠕变中介于理想固体与理想液体之间的力学性质不能够准确描述。因此,将分数阶导数引入岩土蠕变模型建构中能描述这种勾兑特性,并发挥其参数少、形式简单等优点。近年来,岩土工程领域越来越多地引用分数阶微积分理论来描述不同岩土材料的力学特性。殷德顺等[9]将Hollomon提出的金属塑性拉伸变形方程式引入岩土工程中,并在分数阶导数基础上给出了恒应变率加载情况下的土应力应变关系。Hou等[10]考虑应力引起的强弱化效应对冻土蠕变的影响,提出了一种分数阶蠕变本构模型。此外,一些学者还将分数阶导数理论应用于元件模型中[11-14],得出了相关的分数阶蠕变模型。
分析西安某煤矿黏土在不同温度、不同含水率及加载应力下的单轴蠕变试验曲线,得到其对冻结重塑黏土蠕变特性的影响规律。在经验模型的基础上引入分数阶导数理论,建立冻结温度、含水率和加载应力相互影响的人工冻结重塑黏土分数阶蠕变模型。
1 人工冻土力学试验
1.1 人工冻土单轴抗压、蠕变试验
所用土样取自西安某煤矿黏土,取样深度为10~20 m,将土样加工成高度100 mm、直径50 mm的圆柱体试样(见图1),用WDT-100型微机控制电液伺服冻土试验机进行单轴抗压试验和单轴蠕变试验[15]。试验土样物理性质指标参数见表1。

表1 试样物理性质指标参数

(a)试验前

(b)试验后
1.2 试验结果与分析
根据单轴抗压强度试验,得到冻结重塑黏土在3个含水率及不同温度水平下的单轴抗压强度,如表2所示。

表2 冻结重塑黏土单轴抗压强度
冻结重塑黏土从加载到破坏的应力-应变关系主要经历弹性阶段,塑性阶段和屈服破坏阶段。弹性阶段,随着轴向应力的增大,使得土体密实度增加,土样的承载能力提高,此阶段的应力-应变曲线基本呈线性增长;塑性阶段,随着轴向应力的进一步增大,土体发生不可逆变形,曲线呈非线性增长趋势,应力达到顶峰,土体内部产生裂隙,冰结晶与图颗粒开始破坏;屈服破坏阶段,应力达到顶峰后继续加载,试样承载能力降低,试样进入软化阶段,且试样随冻结温度的降低,单轴抗压强度逐渐增大,结果如图2所示。

图2 不同条件下冻结重塑黏土应力-应变曲线
如图3所示,冻结重塑黏土含水率分别为12%、16%和20%以及温度为-5 ℃、-10 ℃和-15 ℃的条件下开展无侧限单轴抗压强度试验,得到抗压强度与含水率、冻结温度间的关系图,温度、含水率和抗压强度满足

图3 抗压强度与含水率、冻结温度关系
σs=-20-0.35T-760ω2+255ω,R2=0.98
(1)
随着冻结重塑黏土含水率的增加,其强度呈先增大后降低趋势,含水率约16%时强度达到最大。原因是在含水率处于较低水平时,含冰量的多少决定冻土的强度,同等温度下,含水率增加导致含冰量相应增大,冻结重塑黏土颗粒间冰胶结力增大,内聚力增强,从而导致强度增大。当含水量达到最优含水率后,随着水分含量增加,内部未冻水含量增多产生润滑作用,导致黏土颗粒间摩阻力降低,强度下降。
2 人工冻土分数阶蠕变模型
2.1 分数阶微积分的定义
β是一个正实数,令n-1<β≤n,一个定义在[a,b]区间上的函数f(t)的β阶分数阶积分的定义是
(2)
它的另一个表达形式为
(3)
其中Γ(z)表示通常的Gamma函数,即
(4)
关于分数阶微积分有很多定义,其中Riemann-Liouville分数阶微积分算子理论对函数f(t)的β阶分数阶积分的定义为
(5)
对于函数f(x)=zx,z为常数,其分数阶微分为
(6)
当取t=v0τ时,其中v0为常数,则
(7)

(8)
2.2 分数阶蠕变模型的建立及参数确定
根据《人工冻土物理力学性能试验》[16]可知,以幂函数的组合形式能够描述人工冻土蠕变特性,建立经验模型
(9)
式中:ε为轴向应变;T为冻结温度,单位为℃;t为时间,单位为h;A、k、b、c均为模型参数,k、b、c分别反映了冻土变形发展受温度、加载应力、时间影响的敏感性;σ=ησs;η为蠕变加载系数,为0.3或0.5;σs为单轴抗压强度。
冻结重塑黏土的应力应变特性是介于理想固体和理想流体之间的某种关系,式(9)未能反映该种特性,而分数阶导数能够准确描述该种关系,对式(9)进行分数阶微分得到
(10)
(11)

分别将各含水率、温度和加载等级下的应变与时间取对数,发现在同一含水率和加载等级下,不同冻结温度条件下的应变与时间取对数时具有线性关系,因此将各含水率下不同加载系数及不同温度的试验值分别代入建立的模型中,联立方程组对模型参数进行求解。对式(11)两边同时取对数有
lgε=lgB+blgσ+βlg v0-lg Γ(2-β)+(1-β)lgt
(12)
图4为对各含水率和不同温度下的试样进行加载,加载等级为0.3σs和0.5σs的lgε-lgt拟合关系。可以发现:
(1) 在图4中,-5 ℃、-10 ℃、-15 ℃三个温度下的lgε-lgt拟合曲线斜率近似平行,试样蠕变变形值lgε随着温度的降低而减小。这是由于土中未冻水的含量逐渐减少,其抵抗变形的能力逐渐增大,蠕变变形值逐渐降低。
(2) 由图4(b)、图4(c)可以发现,加载系数不同而拟合曲线斜率同样近似平行,相同含水率和温度下,拟合曲线截距随加载系数的增大而增大。
综上,冻结重塑黏土蠕变的lgε-lgt拟合曲线斜率均近似相等,其截距的值与含水率、加载系数及温度有关。

(a)含水率 12%,加载系数0.5

(c)含水率16%,加载系数0.5

(d)含水率20%,加载系数0.5
2.2.1 参数β的确定
含水率为12%时,加载系数0.3σs下,温度分别为-5 ℃、-10 ℃、-15 ℃的线性表达式为
(13)
含水率为12%时,加载系数0.5σs下,温度分别为-5 ℃、-10 ℃、-15 ℃的线性表达式为
(14)
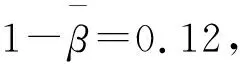
2.2.2 参数B和b的确定

lgB1+b1lg 0.3σs-lg Γ(2-β)=0.42
(15)
lgB1+b1lg 0.5σs-lg Γ(2-β)=0.75
(16)
计算出含水率为12%时,T=-5 ℃的参数B1、b1的值,B1=8.86,b1=1.49。
同理求出不同的含水率与加载系数对应的B和b的值(见表3)。
由表3及图5、图6可知,温度与含水率对冻结重塑黏土蠕变特性均有较大影响。蠕变模型参数B的值随着温度的降低不断减小,而b值变化不大。温度-5 ℃时参数B在20%含水率下所得的值要小于在16%含水率下的值,表明在同种温度条件下,接近最优含水率的冻结重塑黏土延性更大,达到破坏所需时间增加,导致蠕变推迟。大于最优含水率的冻结重塑黏土延性降低,达到破坏所需时间减少,加速蠕变提前。

表3 不同温度、含水率条件下参数B和b的值

图5 冻结重塑黏土参数B与温度关系曲线

图6 参数b(T,ω)三维拟合图
由上述整理得,温度T和含水率ω与B和b拟合关系式为
(17)
b=0.009 6T+12.96ω-0.068
(18)
将参数B和b代入式(11),得出与温度和含水率有关的分数阶冻结重塑黏土蠕变模型为
(19)
根据推导出的分数阶冻结重塑黏土蠕变模型计算出该重塑黏土冻结状态下的蠕变值,将计算得出的结果与试验值对比,结果如图7所示。
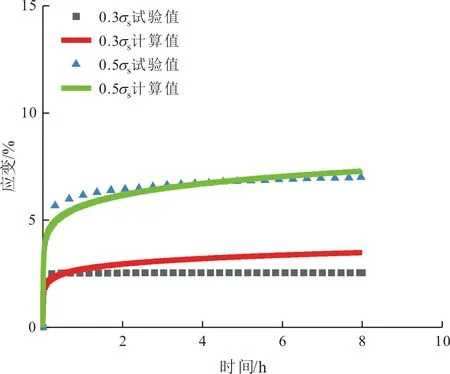
(a)温度-5 ℃,含水率12%

(b)温度-15 ℃,含水率12%

(c)温度-15 ℃,含水率16%

(d)温度-5 ℃,含水率20%

(e)温度-10 ℃,含水率20%
由图7可知,总体上该经验模型计算值与试验值吻合程度较高,对不同含水率、不同温度及加载等级下冻结重塑黏土蠕变值模拟结果较为准确。其中图7(e)和图7(f)在0.5σs荷载等级下的试验值与计算值出现偏差,分析原因可能是含水率较高,试样内冰结晶的分布不均,且温度越低,使得试样中的冰结晶强度越大,造成单轴强度偏差越大,导致蠕变加载应力偏差越大,以致试验值较计算值偏差越大。
3 结论与展望
鉴于以幂函数组合形式建立的经验模型在描述人工冻土蠕变特性和确定模型参数等方面的不足,基于分数阶导数理论,建立能在不同温度、不同含水率及加载强度条件下的冻结重塑黏土分数阶蠕变模型。所建模型具体结论如下:
(1) 通过在常见的蠕变模型中引入分数阶导数,能够很好地反映冻结黏土蠕变介于理性固体和理想流体之间的某种勾兑特性。
(2) 建立的冻结重塑黏土分数阶蠕变模型参数在不同冻结温度和含水率下,对不同加载应力产生的蠕变与时间取对数联立方程均具有物理意义且易于确定,便于工程应用。
(3)所建冻结重塑黏土分数阶蠕变模型计算结果曲线与试验曲线吻合度较高,表明该模型能够较好地描述冻结重塑黏土在单轴压缩状态下不同温度和不同含水率的力学行为。
针对个别组分数阶蠕变模型计算值和试验值偏差较大的现象,将进一步完善试验方案,如在蠕变试验中增加0.7荷载等级加载和增加冻结温度为-20 ℃的试验,加大试验量为下一步优化模型参数积累试验数据。冻结重塑黏土蠕变特性除了受冻结温度、含水率和加载应力影响外,还受损伤、固结压力及应力历史等因素的影响。因此,建立考虑冻结重塑黏土主要因素影响的分数阶蠕变模型是下一步的研究目标,以便研究结果更好地服务实际工程。

