考虑碳交易和无功补偿的分布式电源优化配置

孙健浩，初壮

（东北电力大学电气工程学院，吉林省 吉林市 132012）

0 引言

近年来，分布式电源(distributed generation，DG)由于具有节能环保、能源利用率高、配置灵活等特点，得到了迅速发展，成为我国发展智能电网重要的组成部分[1-4]。为了响应“碳达峰、碳中和”战略目标，同时减少DG并网给系统带来的不利影响，通过碳交易和无功补偿等机制引导电力行业进行DG的优化配置，被认为是促进可持续发展的重要举措。合理的DG优化配置是保障电力系统运行灵活性、可靠性、安全性的前提[5]。因此，有必要在DG的优化配置中引入碳交易和无功补偿等机制。

目前，针对DG优化配置问题，国内外学者已经开展了多方面的研究。文献[6]以无功损耗和电压偏移最小化为目标，采用灰狼算法对配电网中的DG进行选址定容。文献[7]基于两阶段优化模型，考虑供电可靠性，从而对区域的风储电站进行规划。文献[8-9]考虑网损和电压稳定性2个目标，提出了一种DG优化配置方法，从而增强系统的带载能力及可靠性。通过以上分析可知，目前多数研究仅考虑配电网中DG的优化配置，并未考虑无功补偿。然而无功补偿是电力系统中电能质量的重要保障手段之一，对系统中的无功源进行合理配置，有利于提高节点电压水平、降低系统网损，使系统安全稳定运行[10]。文献[11]在DG选址定容的问题上考虑了无功优化，并分析对比了DG满出力与零出力时系统的稳定性与可靠性。文献[12]提出了通过负荷节点电压稳定裕度确定系统中无功补偿点，并以有功网损最小为目标对系统无功源进行合理配置。以上研究虽然考虑了无功补偿给系统带来的影响，却忽略了环境问题。

目前碳交易机制被认为是最有效的碳减排措施之一，即将CO2排放成本计及电力生产成本中，从而达到节能减排的目的[13]。文献[14-15]为提高电力系统对光伏发电的接纳能力，将阶梯型碳交易机制引入电力系统经济调度中，提出了一种基于碳交易的复合储能优化调度模型。文献[16]建立了基于碳交易的燃气机组规划模型，以系统综合成本最小为目标进行低碳电源的规划。文献[17]通过搭建碳-绿色证书联合交易市场框架，对综合能源系统进行了日前优化调度。文献[18]将碳交易机制应用于南方电网西电东送电量的优化模型中，为碳交易机制的实际应用提供了参考。

基于以上分析，本文提出了一种考虑碳交易和无功补偿的DG优化配置模型，以规划期内综合成本最小为目标函数，对系统中光伏、燃气轮机及无功补偿装置的位置及容量进行规划，采用改进的自适应遗传算法(genetic algorithm，GA)进行求解。最后，选取IEEE33节点配电系统构造算例，通过仿真分析验证模型的正确性。

1 碳交易机制

1.1 碳交易配额模型

目前，我国的碳交易市场仍处于初期阶段，碳排放份额往往免费地分配给参与碳交易机制的发电企业[19]。本文采用碳排放份额与发电量成正比的分配方式，同时认为配电网内的碳排放主要来源于从上级火力发电厂购买的电力。因此，无偿碳排放配额可表示为

式中：η为单位电量无偿碳排放配额；λ为燃气轮机单位电量无偿碳排放配额；T为碳交易费用的结算时间，其值为1 a；Pgrid(t)为配电网向上级发电厂购买的电力；PMT(t)为燃气轮机年发电量。

1.2 碳排放量计算模型

本文所提到的配电网碳排放量包括2部分：一是由配电网中有功负荷所需电量引起的碳排放；二是由配电网中各支路损耗所引起的碳排放。系统碳排放量可表示为

式中：δ、μ分别为外购单位电量、微型燃气轮机的碳排放强度；Tloss为年最大负荷损耗时间；Tmax为年最大负荷利用时间；N为配电系统中支路条数；Ploss,k,t为支路k在t时刻所损耗的功率；n为系统中负荷节点数量；Ptotal,i,t为t时刻第i个节点负荷功率；PMT,t为t时刻微型燃气轮机释放的电量。

1.3 碳交易成本模型

根据上述碳交易配额模型及碳排放计算模型，当发电企业的实际碳排放小于政府分配的碳排放配额时，可以售卖多余的碳排放权，从而获得收益；反之，发电企业必须购买碳排放权来补偿超出的碳排放量。碳交易成本模型表示如下：

式中：fCO2为碳交易成本，fCO2>0时，表示系统需要购买碳排放权成本，fCO2<0时，表示系统出售碳排放权所获利成本；CCO2为单位碳交易价格。

2 考虑碳交易和无功补偿的DG双层优化配置模型

本文构建的双层优化配置模型包含2个优化任务：上层为DG的优化配置，以配电网规划周期内的年等值成本、年运行成本、碳交易成本最低为目标，决策变量为光伏及燃气轮机接入配电网的位置及容量；下层为无功补偿电容器的优化配置，以配电网的网损最低、电压稳定性最高为目标，决策变量为无功补偿电容器的安装位置及容量。上层将DG的优化配置结果传递给下层，下层根据已知DG的信息求解最优配置结果并回馈给上层，通过改进的自适应遗传算法的反复迭代，得到两者的最优配置结果。

2.1 上层优化模型

2.1.1 上层目标函数

上层目标函数的具体表达式如下：

式中：fzs为DG的年等值投资成本；fPV和fMT分别为光伏和燃气轮机的年等值投资成本；NPV、NMT分别为光伏和燃气轮机的数量；SPV,i、SMT,i分别为第i台光伏和燃气轮机的安装容量；fcr为折旧系数；CPV、CMT分别为单位容量光伏和燃气轮机的投资成本；CPVM、CMTM分别为单位容量光伏和燃气轮机的运行成本；r为年等值回报率；Y为规划年限；fyx为年运行成本，表达式为

式中：Closs为配电网损耗费用；Cpe为负荷电费；γ为配电网购电的单位电价；NG为系统中DG的数量；Ploss,k为第k条支路的有功损耗；Ptotal,i为第i个节点负荷的有功功率；PDG,i为第i个DG的有功功率。

2.1.2 上层约束条件

1）功率平衡约束

功率平衡约束条件如下：

式中：PG,i为发电机向节点i输入的有功功率；Pload,i为节点i的有功负荷；Ui、Uj分别为节点i、j的电压幅值；Gij、Bij为线路ij的导纳；δij为节点i、j间的电压相角差。

2）节点电压约束

节点i的电压约束条件如下：

式中Umin、Umax分别为Ui的最小值和最大值。

3）DG总容量约束

本文设定接入DG的总容量不大于总负荷有功功率的20%，即

4）碳交易量约束

根据碳交易机制的本质，系统中碳排放量、碳交易配额、碳排放权之间应满足以下约束条件：

式中Eb、Es分别为发电企业从电力市场购买、出售的碳排放权。

2.2 下层优化模型

2.2.1 无功补偿点的确定

本文通过计算系统中的节点电压稳定指标，并与设定的电压稳定裕度门槛值进行对比，选取系统中电压稳定性较差的节点作为无功补偿点，节点电压稳定指标如下：

式中：Pj、Qj分别为节点j送出的有功功率和无功功率；Rij、Xij分别为支路ij的电阻和电抗。

2.2.2 下层目标函数

下层优化规划主要以无功补偿装置等年值投资费用、系统网损以及电压偏移量最小为目标，从而确定无功补偿点所需的无功容量。由于综合目标函数中各子目标所代表的物理含义不同，存在量纲上的差异，为了解决这个问题，本文基于标幺值的概念，以各子目标对应最优解作为基准值，对综合目标函数进行无量纲化处理。具体表达式如下：

式中：fpy为系统电压总偏移量；fpy,i为节点i的电压偏移量；floss为系统总网损；fwf为无功补偿装置的等年值投资费用；ωpy、ωloss、ωwf分别为各子目标的权重；分别为各子目标对应的基准值；Nc为无功补偿装置的数量；Qc,i为第i个无功补偿装置的补偿量；Cc、Cch、Ccs分别为单位容量无功补偿装置投资成本、运行维护成本及回收成本；fhs为回收系数。

2.2.3 下层约束条件

1）无功平衡约束

无功平衡约束条件如下：

式中：QG,i为发电机向节点i输入的无功功率；QW,i为节点i的无功补偿量；Qload,i为节点i负荷的无功功率。

2）不等式约束

不等式约束条件如下：

式中：ULi为负荷节点i的电压；ULi,min、ULi,max分别为ULi的最小、最大值；QCi为节点i的无功补偿器补偿容量；QCi,min、QCi,max分别为QCi的最小、最大值；NL、NC分别为负荷节点数、无功补偿点数。

3 模型求解

遗传算法是根据生物进化论原理来搜索全局最优解集，该算法目前广泛应用于规划等复杂问题求解[20-21]。

3.1 改进的自适应遗传算法

传统遗传算法中的交叉、变异概率为确定值，不能体现生物进化过程中的自适应特征，容易出现早熟收敛、局部最优等问题[22]。因此，本文针对DG的规划问题对算法的交叉、变异概率进行适当改进，改进后的公式如下：

式中：Pc、Pm分别为自适应交叉、变异概率；Pc1、Pc2和Pm1、Pm2分别为2个父代个体的自适应交叉、变异概率；k1为自适应调控参数；f'为2个父代个体中适应度较大的值；favg、fmax分别为当前种群的平均适应度与最大适应度。

3.2 求解流程

模型具体求解步骤如下：

1）设置算法的环境变量参数，如变异、交叉概率，以及种群规模、迭代次数等。

2）根据步骤1）的参数初始化种群，并在MATLAB中通过前推回代潮流计算的方法，判断种群中的个体是否满足约束条件，清除无效个体，得到有效种群。

3）将有效种群进行上层优化，计算目标函数值、每个个体的适应度及种群适应度平均值等参数，将当代最优个体传递给下层优化。

4）通过上层优化的最优个体，计算下层目标函数值和个体适应度，记录当代的最优个体，保存当代最优配置结果。

5）对种群进行赌轮选择和自适应交叉、变异等操作，将产生的新种群传递到步骤2）进行循环迭代计算，当达到最大迭代次数时，停止循环，输出最后一代种群最优配置结果。具体流程如图1所示。

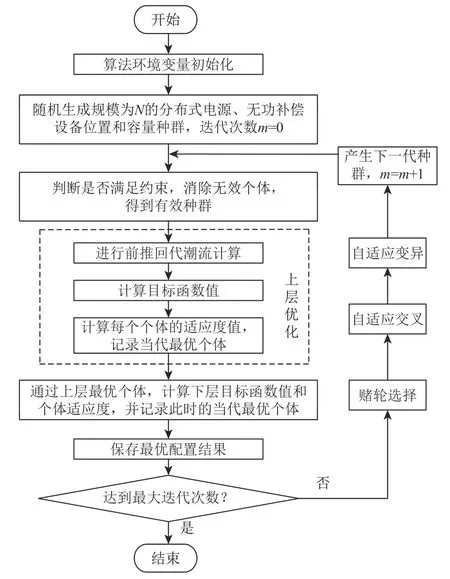
图1 求解流程图Fig.1 Solution flow chart

4 算例分析

4.1 基本参数

为验证本文模型的正确性，选取IEEE33节点配电系统(见图2)构造算例，系统数据参考Matpower7.1中case_ieee33文件，基准电压为12.66 kV，基准容量为10 MV⋅A，将DG等效为功率因数为0.9的PQ节点，总接入DG容量不大于总负荷的20%，各节点无功补偿上限为300 kV⋅A。其他仿真数据如表1所示。

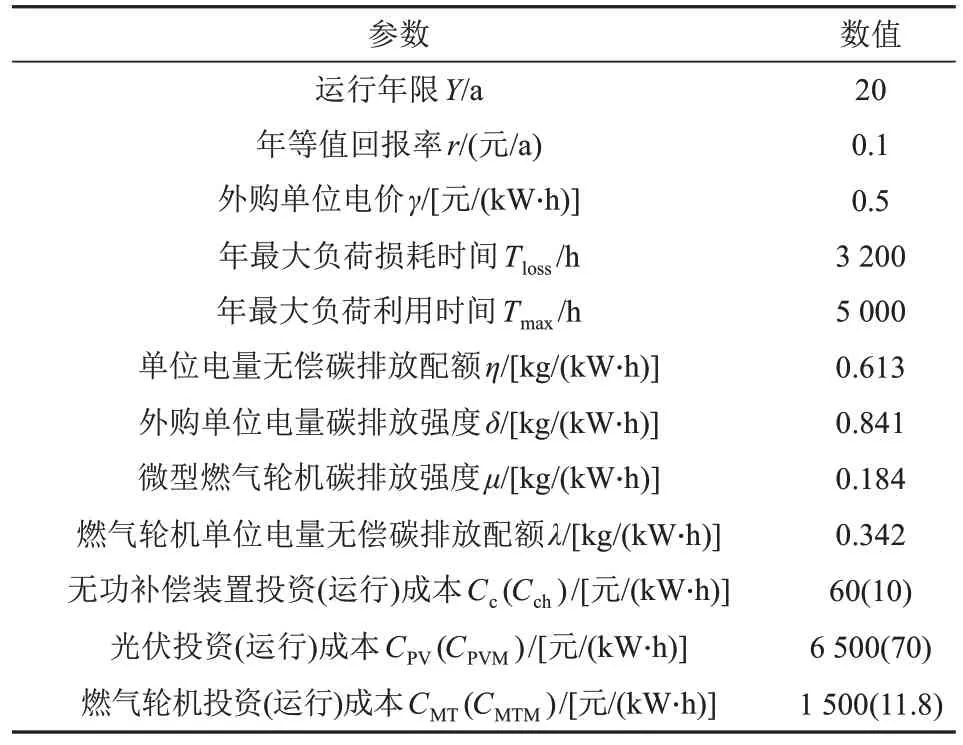
表1 仿真数据Tab.1 Simulation data

图2 节点系统图Fig.2 Node system diagram

自适应遗传算法参数设置如下：种群数N为100；最大迭代次数M为200；Pc1取值为0.9；Pc2∊[0.5,1]；Pm1取值为0.1；Pm2∊[0.5,1]。

4.2 结果分析

表2为系统节点电压稳定裕度次序表，稳定裕度越小，对应节点的电压稳定性就越差，越需要无功补偿，本文设定电压稳定裕度门槛值为0.7，因此选择表2中排序前12位的节点作为无功补偿点，则补偿点的集合为A={19, 18, 17, 16, 33,15, 32, 31, 14, 13, 30, 29}。

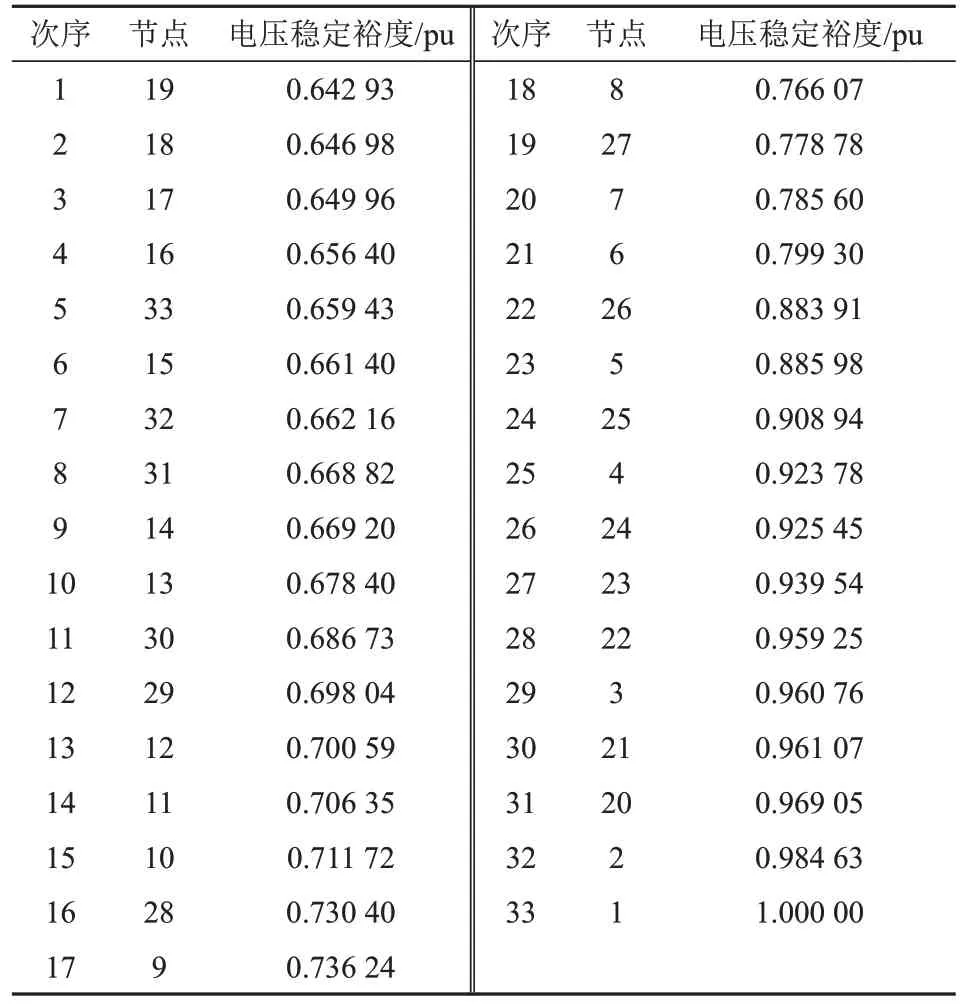
表2 节点电压稳定裕度次序表Tab.2 Node voltage stability margin sequence table

为了说明系统在DG优化配置时考虑碳交易与无功补偿的优越性，设置以下4种方案对比碳交易和无功补偿对DG优化配置的影响，表3为不同方案下优化配置结果。

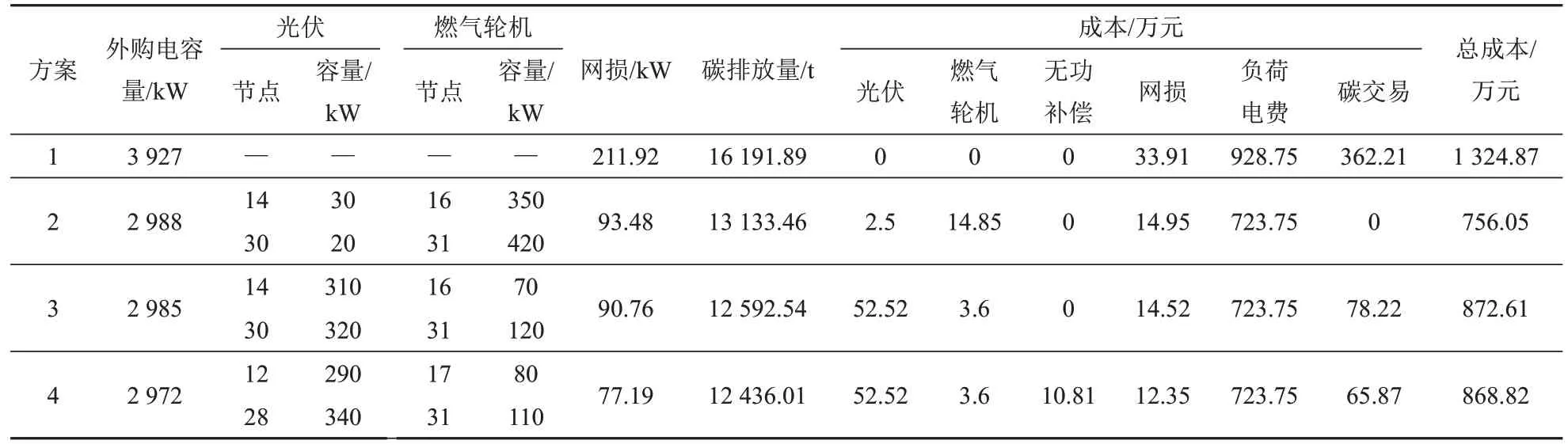
表3 不同方案下优化配置结果Tab.3 Optimized configuration results under different schemes

方案1：系统考虑碳交易机制而不接入DG。

方案2：系统不考虑碳交易机制而接入DG。

方案3：系统既考虑碳交易机制又接入DG。

方案4：在方案3的基础上考虑无功补偿。

通过对比表3中方案1、3可知，在考虑碳交易机制的基础上，虽然DG并网增加了运行投资费用，但系统从上级购买电量下降了约24%，负荷电费降低了22%，网损也降低了约57%，年碳排放量降低了3 774.16 t，年碳交易成本降低了283.99万元，系统总成本降低了34%，说明DG的接入有利于提高系统的经济性及环保性。

通过对比表3中方案2、3可知，系统DG的容量配置由光伏50 kW、燃气轮机770 kW变为光伏630 kW、燃气轮机190 kW，碳排放量降低了4.1%，这是由于当系统考虑碳交易机制时，燃气轮机产生的碳排放量转换成碳排放成本，间接增大了燃气轮机的运行成本，而光伏是清洁能源，不产生碳排放，所以系统会权衡光伏、燃气轮机的投资运行成本及碳排放成本，对其容量进行配置，因此在进行DG的优化配置时应考虑碳交易机制的影响。

通过对比表3中方案3、4可知，虽然系统增加了无功补偿装置费用，但是总成本却降低了0.4%，这是由于计及无功补偿之后，系统潮流发生变化，DG的配置发生了改变，受其影响所减少的网损费、碳交易成本等弥补了无功补偿装置的费用，因此系统总效益更优。

表4为方案4下最终双层优化配置结果，可以看出：DG接入总容量为820 kW，小于系统总负荷有功功率的20%，满足模型约束。同时结合图2可知，系统中由于线路末端传输功率比较长，DG安装于末端有利于就地提供功率，从而降低了系统线路损耗，验证了本文所提模型和方法的合理性和有效性。

表4 最终双层优化配置结果Tab.4 Final double-layer optimal configuration results

为进一步说明在规划配电网DG的同时配置无功补偿装置的优越性，设置以下4种方案对系统节点电压水平、电压偏移量以及节点电压稳定裕度进行对比：1）优化前原始网络；2）系统仅DG接入；3）系统仅装设无功补偿设备；4）系统中装设DG和无功补偿设备。图3、4为对比结果。

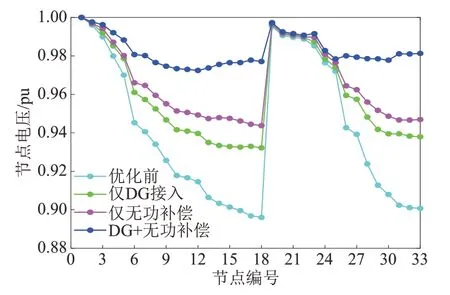
图3 节点电压对比图Fig.3 Node voltage comparison diagram

图4 电压偏移量与稳定裕度对比Fig.4 Comparison of voltage offset and stability margin

通过对比图3、4中方案1、2可知，DG的接入对系统的影响表现如下：随着DG的接入，系统的节点电压水平、电压稳定裕度都有所提高，系统电压偏移量也降低了31%，说明DG的接入有利于提高系统运行的稳定性。

通过对比图3、4中方案2、3、4可知：方案4较方案2、3电压偏移量明显降低，电压稳定裕度有所提高；方案4的节点电压效果最好，方案3次之，方案2较差。方案4的节点电压最低维持在0.972 pu，比方案2最低电压高出0.039 pu，这不仅体现了电压降落与无功功率的关系较有功功率更为紧密，而且说明了无功补偿装置的接入避免了系统在DG启停或出力变化时出现电压失衡、稳定性较差等问题，保证了系统运行的稳定性和可靠性，验证了DG优化配置时考虑无功补偿的合理性及优越性。

4.3 算法改进结果分析

图5为采用改进自适应遗传算法与传统遗传算法求解本文所提双层优化配置模型时的收敛对比曲线。可以看出，改进的自适应遗传算法较传统的遗传算法求解效果更精确，收敛速度更快，这是由于改进的自适应遗传算法在寻优过程中进行了赌轮选择、自适应交叉及变异操作，同时配合精英保留策略有效改善了算法的全局最优搜索能力，避免过早地陷入局部最优，极大地提高了算法的收敛性及求解结果的准确性。

表5为2种算法的寻优对比结果，可以看出，改进的自适应遗传算法在求解时间、迭代收敛次数及总成本方面均明显优于传统的遗传算法。

表5 算法寻优对比结果Tab.5 Comparison results of algorithm optimization

5 结论

构建了考虑碳交易和无功补偿的配电网优化系统，建立了双层优化模型来优化DG的布点位置及容量，通过算例分析可得出如下结论：

1）考虑碳交易机制会影响不同种类电源配置容量的大小，系统的碳排放量、碳交易成本及总成本明显降低。

2）考虑无功补偿后，配电网的网损、电压水平及节点电压稳定裕度都得到不同程度的提升，同时保证在DG不出力时配电网电压能维持在合理的范围内，降低了DG出力不确定性对配电网的影响。

3）在对配电网中的DG进行优化配置时，碳交易与无功补偿机制的同时引入会使系统更具有环保性、经济性和稳定性。

4）改进的自适应遗传算法在求解效率及准确性上均优于传统的遗传算法，表明在算法中引入赌轮选择、自适应交叉及变异、精英保留策略，能提高算法的全局最优搜索能力，避免过早地陷入局部最优。