基于AdaBoost算法的混凝土抗压强度预测
胡 畔,肖 约,汪 芳,唐文泽,周 华
1. 武汉理工大学土木工程学院,湖北 武汉 430070;
2. 华杰工程咨询有限公司中南分公司,湖北 武汉 430000;
3. 武汉华夏理工学院建筑与土木工程学院,湖北 武汉 430223;
4. 武汉安宇工程建设管理有限公司,湖北 武汉 430040
混凝土由不同的成分组成,这些成分随机分布在整个混凝土基体,如此复杂的系统使得准确预测混凝土抗压强度成为巨大的挑战。通常获取混凝土抗压强度最直接的方法是通过物理试验,但这种方法相对耗时、繁琐且昂贵。有学者还提出了一些经验回归方法来预测混凝土中不同组分的给定设计配合比的混凝土抗压强度,但混凝土配合比与抗压强度呈现出非线性关系,难以得到准确的回归表达式[1]。近些年,许多学者开始使用机器学习来预测混凝土抗压强度。Pham 等[2]通过最小二乘支持向量回归(least square support vector regression,LS-SVR)与萤火虫算法(firefly algorithm,FA)耦合方法来预测高性能混凝土抗压强度。Bui 等[3]将优化改进后的FA 算法与人工神经网络(artificial neural network,ANN)结合来设置权值和阈值。Tien Bui等[4]比较了基于鲸鱼(whale optimization algorithm,WOA)、蜻蜓(dragonfly algorithm,DA)与蚂蚁(ant colony optimization,ACO)觅食行为的有效元启发式技术在预测28 d混凝土抗压强度方面的效率优化,这些算法与ANN 耦合,以优化权值和阈值。Duan 等[5]测试了各种机器学习工具和自适应模糊神经网络(adaptive neuro fuzzy inference system,ANFIS)与独立成分分析(independent component analysis,ICA)耦合,用于预测再生骨料混凝土抗压强度。
在实际施工过程中,由于不同操作者的主观判断和操作方式不同,加上现场环境条件的变化,实测的混凝土28 d 抗压强度会改变。能否准确预测混凝土的28 d 抗压强度,是保证正常施工速度和减少返工的重要前提。
基于此,本文提出一种基于自适应增强(adaptive boosting,AdaBoost)算法的混凝土抗压强度预测模型,收集1 030 组混凝土抗压强度试验数据,以混合物含量与养护时间为输入数据,以抗压强度为输出数据。然后介绍AdaBoost的基本数学背景和相应的算法实现。利用收集到的数据训练基于AdaBoost 算法模型,得到了一个可用于预测抗压强度值的强学习器。采用10 折交叉验证方法对所开发的模型进行验证,并使用包含103 组样本的数据集来证明模型的泛化性。AdaBoost 算法与独立机器学习ANN 和支持向量机(support vector machine,SVM)[6]模型进行性能对比,表明了集成学习算法的优越性。最后讨论了AdaBoost算法模型中一些关键因素(如训练数据的数量、弱学习者的类型以及输入变量的数量)的影响。
1 数据资料分析
建立预测模型需要大量关于混凝土抗压强度试验数据。本研究采用由Yeh[7]收集的1 030 份混凝土抗压强度试验,它包含了1 030×9 组数据,前7 组数据为每立方混凝土内各种原材料(水泥、高炉矿渣粉、粉煤灰、水、减水剂、粗骨料和细骨料)的配比,第8 组为混凝土养护时间,第9 组为混凝土抗压强度。表1 给出了所使用的数据集的变量约束因素。
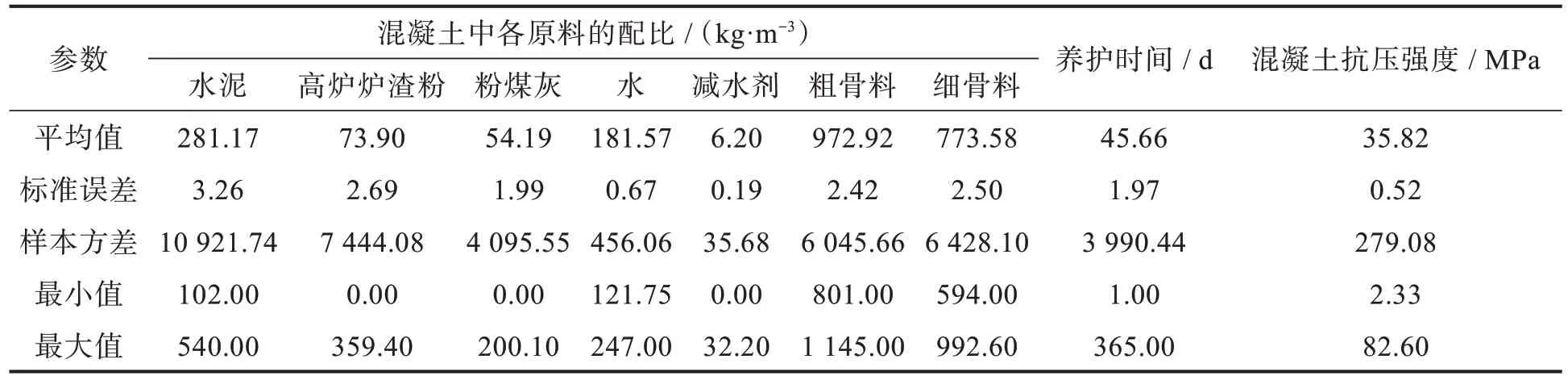
表1 混凝土抗压强度变量约束因素Tab.1 Constraining factors of concrete compressive strength variables
2 AdaBoost算法
Freund 和Schapier[8]在20 世纪90 年代提出了AdaBoost 算法。它是利用初始的训练数据生成一个弱学习者,然后根据下一轮弱学习者训练的预测性能调整训练数据的分布。
2.1 数学背景
采用AdaBoost 算法预测混凝土抗压强度,其步骤如下:
(1)初始训练数据集D={(x1,y1),…,(xn,yn)},其中:n表示样本的数量;xi(i= 1,2,3,…,n)表示一条数据样本;yi(i= 1,2,3,…,n)是对应实际值。
(2)初始化n个样本的权值,首先假设训练集样本权重分布Dk(i)为均匀分布;Dk(i)= 1/n,Dk(i)表示在第k次迭代中训练集样本的权值;n为样本的数量;最大迭代次数为K。
(3)在加权样本下训练弱预测器hk(x) ,并计算其平均误差
(5)返回步骤(2),进行下一次迭代,直到迭代次数达到K后结束。
2.2 实现过程
AdaBoost算法的实现[9]有4 个阶段:①实验数据的收集;②强学习者的生成;③学习者的测试或验证;④学习者在工程问题中的应用。该程序的流程图如图1 所示。
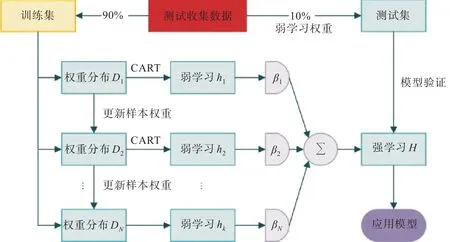
图1 AdaBoost算法流程图Fig.1 AdaBoost algorithm flow chart
2.3 参数设置
AdaBoost 算法参数包括2 个层次:第一层次是AdaBoost 框架;另一层次是弱学习者即回归树(classification and regression tree,CART)[10]的重要参数。根据试错法[11]确定参数值的范围;然后采用网格搜索方法找到特定的值,即从初始值范围内定义一个参数网格,使用交叉验证对模型进行迭代训练和测试,以找到性能最好的参数集。AdaBoost算法参数设置如表2 所示。

表2 AdaBoost算法参数设置Tab.2 AdaBoost algorithm parameter settings
3 模型验证
为了建立AdaBoost 算法模型,将收集到的试验数据分为训练集和测试集[12]。训练集用于产生最终的强学习者,测试集用于显示模型预测抗压强度的准确性。通常在总试验数据集中训练集与测试集的比例为9∶1。
3.1 评估指标
为了更好评估AdaBoost 算法性能,引入4 个指标[13],分别定义为平均绝对误差(mean absolute error,MAE)、平均绝对百分比误差(mean absolute percentage error,MAPE)、决定系数(coefficient of determination,R2)、均方根误差(root mean square error,RMSE),评估指标的计算公式见式(1)~式(4):
式中:yi为第i(i= 1,2,3,…,n)个混凝土抗压强度实际值;y′i为第i(i= 1,2,3,…,n)个混凝土抗压强度预测值;n为混凝土立方体立块数目。其中,R2代表预测值与真实值之间的线性相关程度,R2越接近1 则表示预测值与真实值越接近,模型性能越好。RMSE 表示预测值与测试值之间的偏差。MAE 反映了预测误差的实际情况。
3.2 单9∶1 验证结果
随机选择90%的数据用于训练集,其余10%的数据用于测试集,图2 显示了训练集和测试集的预测抗压强度值和测试抗压强度值之间的线性关系。特别是对于训练集,散点几乎与拟合曲线重合(即预测值等于测试值);而对于测试集,则存在少许离散,说明预测略有偏差。
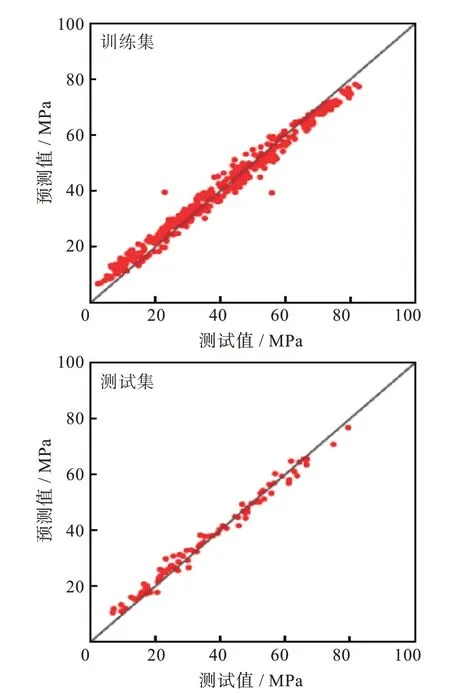
图2 测试和预测的抗压强度之间的线性关系Fig.2 Linear relationships between tested and predicted compressive strength
表3 列出了AdaBoost 算法模型计算9∶1 形式的训练集和测试集的4 个评价指标。由表3 可知,该算法模型在预测精确度方面表现优良。对于训练数据集,R2=0.997,即预测值与测试值几乎相同;MAE 为1.25 MPa,MAPE 仅为5.54%,表明AdaBoost 算法模型的训练数据具有非常强的学习能力。对于测试数据,R2=0.982,非常接近1,MAPE 为6.78%,从工程实践的角度分析,误差很低,说明AdaBoost算法模型具有非常高的精度,可以来预测混凝土抗压强度。

表3 数据集以9∶1 形式的评价指标分析Tab.3 Dataset performance analysis in 9∶1 form
3.3 十折交叉验证结果
为了进一步证明AdaBoost 算法模型的泛化和可靠性性能,论文采用了十折交叉验证方法[14]。它将实验数据样本等分为10 个子集,然后使用9个子集来建立强学习器,剩下1 个子集来验证模型。在连续重复此操作10 次后,可以得到10 次的平均精度。图3 显示了十折交叉验证中每折的4个评估指标值。

图3 10 折交叉验证结果Fig.3 Results of 10-fold cross-validation
由图3 可以看出,10 折的结果有一定的波动,R2最小值为0.890,最大值为0.978;MAPE 最小值为7.96%,最大值为15.27%,这都反映了十折交叉验证法具有较高的准确率。
3.4 与养护时间相关的分析结果
养护时间是AdaBoost 算法模型中的重要影响因素之一。为了证明这一特性,选择了3组混凝土配合比。相关信息见表4,其中养护时间设置为1~365 d。

表4 混凝土配合比的养护时间变化分析Tab.4 Time dependent analysis of concrete mix proportion
图4 显示了AdaBoost 算法模型得到的抗压强度随养护时间变化结果预测。测试数据点几乎都位于时间变化曲线上。3 组曲线具有相似的趋势,即混凝土抗压强度随着养护时间的增加而增加,60 d 前增加较快,60 d 后缓慢增加,120 d 左右趋于稳定。由此说明AdaBoost算法模型在没有常规物理试验的情况下可以有效预测混凝土强度随时间变化的趋势。

图4 混凝土抗压强度的时间相关预测结果Fig.4 Results of time-dependent prediction of concrete compressive strength
3.5 实例验证
为了进一步证明AdaBoost 算法模型的泛化性,文章使用了新数据集作为验证。该数据集包括103 份样品,每份样品有7 种成分,即水泥、水、粗骨料、细骨料、减水剂、高炉矿渣粉、粉煤灰。AdaBoost 算法模型对新数据集的预测结果如图5所示。由图5 可以看出,所提出的模型同样对新数据集产生了良好的预测。预测值与测试值之间的关系非常接近y=x函数线。这些都表明AdaBoost算法模型在预测混凝土抗压强度方面确实具有很高的准确性和泛化性能。

图5 新数据集的预测结果Fig.5 Prediction results for new dataset
4 与不同机器学习之间比较
为了更好验证AdaBoost 算法模型的能力,论文使用了被广泛采用的独立学习方法即ANN 和SVM,预测值与测试值如图6 所示。

图6 不同机器学习技术的结果Fig.6 Results of different machine learning techniques
由图6 可以看出,AdaBoost 算法模型预测的结果显示出更线性的关系,说明它的预测更接近测试值。原因可能是SVM 或ANN 是独立学习算法,而AdaBoost是集成学习算法,它集成了由个体学习算法生成的几个弱学习者,表现良好的弱学习者将获得较高的权值,而弱学习者表现不佳的权值会降低。因此,它可以提供更准确的预测。
5 模型性能分析
5.1 训练数据集数量的影响
模型的性能一定程度上取决于训练数据数量。基于此,论文考虑3 种情况,即总数据分别按照9∶1、8.5∶1.5 和8∶2 的比例进行训练和测试,结果如表5 所示。
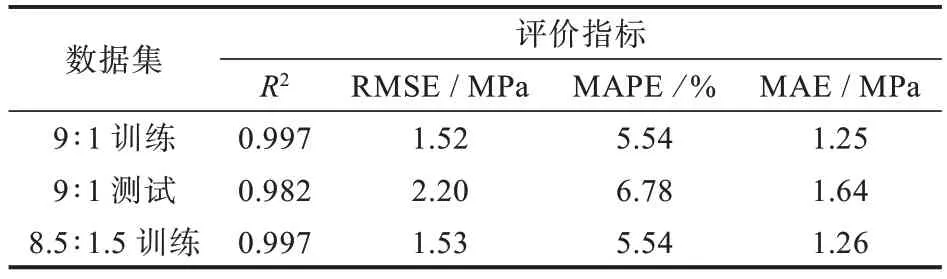
表5 不同的训练数据集数量结果Tab.5 Results for different numbers of training datasets
表5 结果说明这3 种情况都得到了非常高的准确率。对于训练数据集,无论是9∶1、8.5∶1.5 还是8∶2,三者的R2都接近1.0,即预测值与测试值之间的关系是线性的。9∶1 和8.5∶1.5 的RMSE 约为1.52 MPa,而8∶2 的RMSE 为1.55 MPa,说明随着训练数据量的增加,预测偏差会减小。如果使用超过85%的总数据进行训练,MAPE 将降低到5.54%以下,结论与测试数据集结果相似。
当测试数据从整组的80%增加到90%时,R2将从0.979 增长到0.982;MAPE 将从7.78%降至6.78%,说明预测误差和偏差都呈现减小的趋势。
5.2 弱学习者类型的影响
AdaBoost 算法模型的另一个关键因素是弱学习器的选择。与3 种流行的方法即逻辑回归分析(logistic regression,LR)、ANN 和SVM,进行比较,不同弱学习者结果如图7 所示。
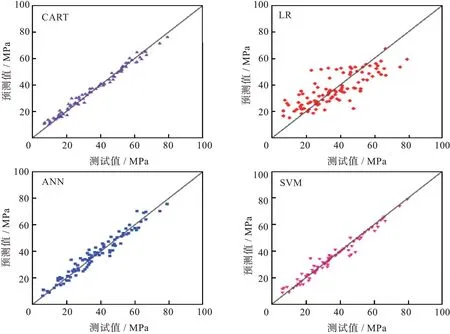
图7 不同弱学习者的结果Fig.7 Results for different weak learners
由图7 可以看出,LR 的评估指标为R2=0.619,RMSE=10.19 MPa和MAPE=31.55%,而对于CART、ANN 和SVM,最差指标是R2=0.960,RMSE=3.30 MPa 和MAPE=8.58%。 而CART、ANN 和SVM 本身已经可以预测输入和输出之间的非线性关系,因此使用集成方法,可以提高模型性能。
5.3 输入变量数的影响
输入不同变量的组合也是影响因素之一,文章考虑了6 种输入组合,如表6 所列。组合1 是原始数据,而组合6 只有4 种输入即水泥、水、粗骨料和细骨料。组合2~组合5 逐渐忽略不同的输入变量观察影响。

表6 不同输入变量组合及相应的评估指标Tab.6 Combinations of different input variables and their corresponding evaluation indicators
6 种组合的预测值与测试值的结果如图8 所示,相应的评估指标也列在表6 中。可以肯定的是,组合1 的结果最好,原因在于它提供了整体信息输入。组合6 的性能最低,其R2=0.377,RMSE=13.04 MPa 和MAPE=41.30%。模型的准确性不会简单地随着输入变量数的增加而增加,如组合2~组合5 的结果。虽然组合2 有7 个输入变量,但它的精度最低(R2=0.398,RMSE=12.82 MPa 与MAPE=40.36%),因为未考虑最重要的变量养护时间。作为比较,组合3 也有7 个输入变量(忽略水泥),其性能明显优于组合2。组合5 只有5 个输入变量,但包含养护时间,因此其性能优于组合2与组合6。组合4 虽然只有6 个输入变量,却有好的评估指标结果(组合1 除外)。

图8 输入变量数量的影响Fig.8 Effects of numbers of input variables
总之,养护时间和水泥是模型中最重要的输入变量,用以获得高精度的预测。忽略养护时间会导致预测精度急剧下降(R2从0.982 降低至0.398),因为随着养护时间增加,水泥继续水合,从而提高混凝土抗压强度;而忽略水泥会导致精度下降相对较小(R2从0.982 降低至0.865),因为水泥通过胶结将混凝土各成分黏结在一起,黏结力越大,混凝土抗压强度越强[15]。忽略一个甚至两个其他约束变量影响不大(R2从0.982降低至0.907)。
6 结 论
通过对1 030 组以及新的103 组混凝土实验数据分析,可以得到如下结论:
(1)AdaBoost 算法模型可以在给定输入变量的情况下准确有效地预测混凝土的抗压强度。同时可以精准预测混凝土在不同养护时间下的抗压强度。
(2)十折交叉验证决定系数R2的平均值达到0.952,平均绝对百分比误差MAPE 达到11.39%,说明预测误差非常低;新的数据集也被用来证明模型的泛化,结果表明AdaBoost 算法模型拥有较高的精度。
(3)在全部变量与养护时间输入,抗压强度输出条件下,AdaBoost 算法模型与ANN、SVM 等独立学习算法进行了比较,其表现明显优于这些模型。
(4)讨论了AdaBoost 算法模型中例如训练数据集数量、弱学习器类型和输入变量的数量等关键因素,发现使用1 030 的80%试验数据集可以获得可接受的结果。选择能够预测输入和输出之间非线性关系的弱学习器(例如CART、ANN 和SVM),它们都可以获得最终强学习器的高精度,而CART 可以达到最佳性能。养护时间、水泥含量是最重要的输入变量,对最终混凝土抗压强度预测有非常大的影响。

