基于BP神经网络的耗占比预测研究
陈瑶,于典,张晓斌
1.安徽医科大学 生物医学工程学院,安徽 合肥 230032;2.安徽医科大学第一附属医院北区 医学工程部,安徽 合肥 230012;3.安徽医科大学第一附属医院 医学工程部,安徽 合肥 230032
引言
自新医改实施以来,耗材管控一直是医疗改革的重点[1-2]。从“两票制”初步尝试降低耗材虚高价格,到“带量采购”限制耗材价格,再到2022年新版绩效考核操作手册中新增“重点监控高值医用耗材收入占比”,耗材的精细化管理及医用耗材收入占比的管控成为医院成本管理的重要研究方向[3-5]。我院是新建三级综合医院,患者量逐年增加,耗材成本也逐年递增。为严格控制医疗成本,改善医疗费用结构,减轻群众就医负担,我院将各科室耗占比考核纳入医院绩效管理方案中。
从整体上看,医用耗材的管控研究可以分为两类:① 偏向于定性分析,通过措施制度等完成管理;② 偏向于定量分析,使用数学模型进行量化预测。定性分析中不少医院通过招标采购、制度落实以及信息化管理系统等精细化手段降低了耗占比[6],比如通过PDCA 分析耗占比高的原因并提出了针对性的改进措施[7-8],或者基于SPD 模式进行耗材的精细化管理探索[9-10],以及基于疾病诊断相关分组构建管理方案[11]。上述定性分析虽然在耗占比管控中取得了一定的成效,但容易被主观因素影响,因此,定量分析方法相对更科学准确。定量分析具体可分为两种思路:① 把耗材变化量作为时间序列进行预测;② 分析耗占比的影响因素,利用医院运营数据建立指标体系并预测耗占比。时间序列预测中,常见的模型有以自回归积分滑动平均模型(Autoregressive Integrated Moving Average,ARIMA)[12]为代表的线性模型以及以长短期记忆神经网络(Long Short Term Memory Neural Networks,LSTM)[13]为代表的非线性模型,但当时间序列数据受到如新科室新耗材引入等因素影响时,精度会受到影响。耗占比具备非线性、波动性、影响因素较多等特点,而反向传播(Backward Propagation,BP)神经网络在非线性和多元统计上表现良好[14-15]。本研究利用我院近2年的运营数据建立神经网络模型,预测每月各科室耗材的使用占比,进而判断科室耗材使用是否合理,为医院绩效考核及管理提供参考依据。
1 资料与方法
1.1 一般资料
本研究以安徽医科大学第一附属医院2021年1月至2023年5月的运营指标为研究对象,具体可分为科室、月份、总收入、药占比、入院人次、出院人次、手术量、平均住院日、病床使用率、病床周转次数10 个指标,并与预测值耗占比构成原始数据集925×11。为更好地评估模型预测性能,选取68×11 为测试集、857×11 为训练验证集,再将训练验证集数据进一步划分为80%训练集和20% 验证集。训练集数据用于建立回归模型,验证集数据用于验证回归模型的性能,最后使用测试集完成模型的测试。
1.2 BP神经网络
BP 神经网络由多层神经元相互连接组成,具体可分为输入层、隐藏层和输出层,见图1。在网络中,同层神经元之间无连接,但每个神经元与下一层所有的神经元相互连接,即每个神经元的输出为下一层神经元的输入。与单个神经元类似,每两个连接的神经元之间都具有对应关系,第i个神经元与下一层第j个神经元权重可记为wij,偏置记为bij,样本个数为n。非线性转换函数定义为激活函数,是为了在网络中引入非线性因素以增强模型的表达能力,因此第o层的输出y(o)的计算方式如公式(1)所示。

图1 BP神经网络结构
BP 神经网络的学习过程分为正向传播和误差的反向传播,流程图如图2所示。正向传播时,输入数据由输入层输入,经过隐藏层逐层处理后,传导至输出层,再通过损失函数计算出输出层的实际输出与期望输出的差异后,进入反向传播阶段。反向传播过程中,首先向网络反馈输出误差,再通过随机梯度下降法或其他优化算法计算并更新权值和偏置后,转入正向传播。正向传播与反向传播反复迭代,直至学习次数达到预定值或误差达到要求为止。

图2 BP神经网络流程图
BP 神经网络具备强大的非线性建模能力,可通过反向传播完成对模型的训练和学习。有很多学者采取BP 神经网络的方法完成预测回归任务[16-21],并取得了良好的成效,因此,依据BP 神经网络建立耗占比预测模型在理论上是可行的。
1.3 基于神经网络的模型实现
1.3.1 数据预处理
为保证输入模型的数据集有效且可靠,需要进一步对原始数据进行处理。原始数据集中包含了因新开科室或重新装修导致的指标空值、医院信息系统导出时出现的异常值、科室为类别型数据的离散特征等。对于指标空值,将其删除;对于异常值,将其替换为零值;对于离散特征的科室指标,考虑到科室较多,若使用Onehot Encoding 会造成特征空间较大,不利于模型的输入,因此本文选择采用Target Encoding 编码方式[22]将不同科室名称编码成可输入模型的浮点型数值,最终生成925×11 的预处理数据,数据的类型如表1所示。

表1 耗占比数据集类型描述
为进一步探究耗占比数据的相关性,本文对数据集中的各指标进行相关性分析。以耗占比为因变量,通过各自变量与耗占比的线性相关程度计算出各指标的Pearson 相关系数,见图3,科室、手术量和总收入与耗占比呈明显正相关,而药占比与耗占比呈明显负相关。考虑到各指标间的非线性关系,以及各指标对耗占比产生的不同程度影响,将各项指标全部保留。

图3 耗占比数据集相关性分析热力图
1.3.2 神经网络模型参数设定
为探究BP 神经网络对耗占比预测的效果,本文搭建了编程语言为Python 3.7、开发框架为Tensorflow 的预测模型进行实验。
在模型训练中,将10 个运营指标作为整个模型的输入,经过隐藏层的计算后,最终通过最后一层输出层输出最终的预测耗占比。损失函数选择均方误差(Mean Squared Error,MSE)函数,计算方式如公式(2)所示。
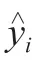
模型优化算法选择自适应矩估计(Adaptive Moment Estimation,Adam)优化器,Adam 吸取了自适应学习率的梯度下降算法和动量梯度下降算法的优点,一方面可以缓解梯度振荡问题,另一方面也可以适应稀疏梯度。具体计算方式如公式(3)~(5)所示。
式中,gt为梯度,β1=0.9 与β2=0.9999 为平滑常数,分别用于计算累计梯度的一阶指数平滑值(mt)与累计梯度的二阶指数平滑值(vt)。通过公式(5)对变量进行更新,θt为模型参数,ϵ、η为常量,ϵ=10-8防止出现除0,η=10-4为设置的学习率。设置Epoch 最大迭代次数为300 次,激活函数选择线性整流函数以增加模型的非线性与稀疏性。
经过测试,最终选定BP 神经网络模型的隐藏层为3 层。层数较少时,网络会因参数较少无法对数据中的各特征进行很好的拟合,导致预测值与真实值相差较多;层数较多时,可能导致模型在训练集上过拟合,在验证集与测试集上表现较差。
1.3.3 模型对比及评价指标
为进一步衡量BP 神经网络模型的先进性,引入了贝叶斯岭回归模型、普通线性回归模型、支持向量机回归模型与梯度提升回归模型进行模型对比。通过设置同等随机数种子与相同归一化参数获取与BP 神经网络模型相同的输入数据,对各模型进行训练后,使用验证集及测试集进一步对比模型。
与此同时,引入评价指标对上述各个模型进行更深层次的对比。评价指标为解释方差(Explained Variance,EV)、平均绝对误差(Mean Absolute Error,MAE)、MSE 与R2。其中,EV 用于解释回归模型的方差得分,计算方式如公式(6)所示,取值范围为[0,1],越接近1 说明预测值越可以解释真实值的方差。MAE 用于评估预测值和真实值的接近程度,计算方式如公式(7)所示,取值范围为[0,+∞),值越小说明回归效果越好。MSE 用于评价预测值与真实值的变化程度,取值范围为[0,+∞),值越小说明回归模型的精确度越好。R2用于反映因变量可通过回归模型被自变量解释的比例,计算方式如公式(8)所示,取值范围为[0,1],越接近1说明模型越精确,回归效果越好。
式中,Var为方差;y为真实值;为预测值。
2 结果
经过300 次迭代后,神经网络迭代损失如图4a所示。在0~50 迭代次数中,网络损失存在明显下降;50~300迭代次数中,网络损失存在波动,但在260 次数后趋于稳定,最后网络损失为1.544×10-8。使用验证集读取训练迭代后的模型权重文件,对BP 神经网络模型进行验证,结果如图4b所示,预测值与真实值比较接近。
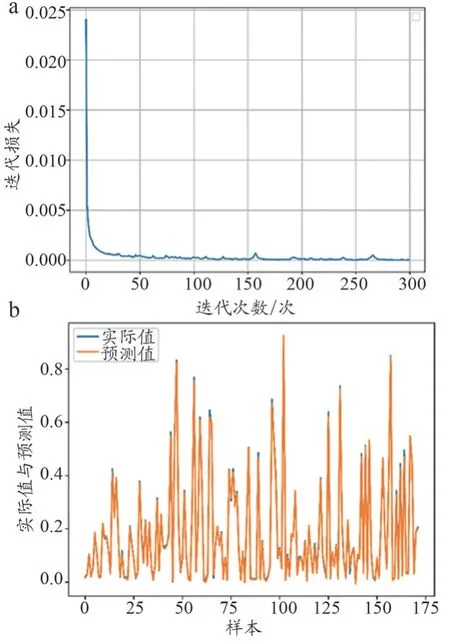
图4 BP神经网络模型结果
各对比模型在验证集上的预测值与真实值对比如图5所示,对各模型在验证集及测试集上进行评价,评价结果如表2~3所示。验证集上,贝叶斯岭回归模型、普通线性回归模型以及支持向量机回归模型表现较差,预测值与真实值接近程度一般;梯度提升回归模型预测值与真实值更为接近,各评价指标均优于贝叶斯岭回归模型、普通线性回归模型和支持向量机回归模型,EV与R2都达到了0.93 及以上,精度良好。BP 神经网络模型的EV 与R2均达到0.99 及以上,且MAE 与MSE 数值相较于上述模型低了不止一个数量级。测试集上,各对比模型评价指标表现比验证集上稍好,梯度提升回归模型EV 与R2均达到了0.95 及以上,而BP 神经网络模型评价指标相较验证集虽有所下降,但EV 与R2均大于0.96,MAE 小于0.03,仍可说明BP 神经网络模型的优势。
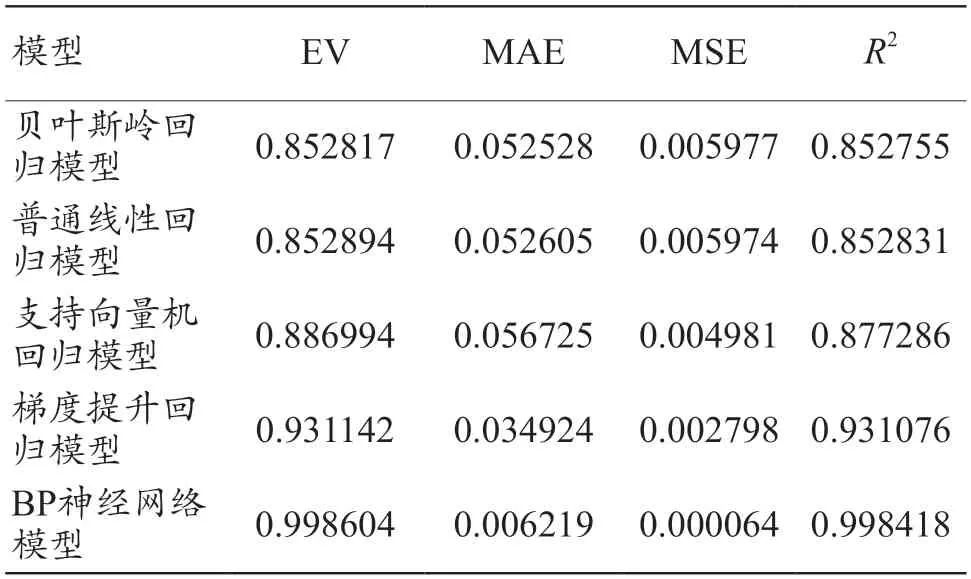
表2 各模型验证集评价指标

表3 各模型测试集评价指标

图5 验证集各模型回归结果对比
3 讨论
本文选取我院2021年1月至2023年5月的数据进行预处理,将857×11 的数据用于训练集和验证集的BP 神经网络模型,剩余68×11 的数据用于测试该模型,验证与测试均取得优秀的结果。通过预测的结果可以直观了解各科室的耗占比数值,为医院管理部门实施绩效考核提供有力的支持,避免耗占比考核中主观判断的经验成分误差。
由于医用耗材的复杂性,建立在定量分析基础上的模型预测很难与实际情况完全匹配。对时间序列预测而言,杨越等[23]使用专家建模器对某型号吻合器使用量进行预测,预测结果R2=0.317。白玲等[24]通过ARIMA模型完成对医院注射器使用量的预测,MAE 为5.308。杨燕等[13]通过LSTM 模型实现了医院静脉留置针领用量的预测,最初预测半年及一季度的R2分别为0.95 与0.97,但当时间序列数据受突发因素影响时,预测半年及一季度的R2值分别为-0.63 与0.33。由于时间序列预测模型更偏向于时间序列对下一个阶段的预测,而医院绩效考核主要评价当下耗占比是否合理,因此本研究基于BP 神经网络模型对各科室耗占比进行预测,验证集R2=0.998418,均优于其他对比时间序列预测模型,测试集R2=0.962357,仅比LSTM 模型中时间序列数据不受突发因素影响时的一季度R2小0.1,这凸显了BP 神经网络模型在利用医院运营数据建立指标体系预测耗占比方面的优势。对于BP 神经网络模型而言,更多的数据量理论上能带来更精确的模型,而测试集各评价指标的降低正是因为医院新科室的建立。新科室的数据量较低于其他科室数据集,在一定程度上导致了模型精度的降低。因此,当前预测模型应及时更新各科室数据,以保证模型的精确度。
4 结论
本文以医院各科室运营指标为研究对象,训练建立BP 神经网络模型预测各科室耗占比指标,预测精度较高,各评价指标均优于其他模型,为医院管理部门对各科室耗材的考核评估提供了量化数据的支撑。但在实际应用中,若新建科室数据量不足,会导致模型精确度下降,因此后续需及时更新科室数据信息,引入更为先进的BP 神经网络模型,完成更精确的评估。

