基于可解释网络解耦表征的低成本雷达定位解算方法

刘磊 林杰

收稿日期：2023-06-25；修回日期：2023-08-24  基金项目：國家自然科学基金资助项目（72071130）；上海市自然科学基金资助项目（22ZR1443300）

作者简介：刘磊（1982—），男（通信作者），黑龙江大庆人，副教授，硕导，博士，CCF会员，主要研究方向为复杂系统（Liulei@usst.edu.cn）；林杰（1998—），男，湖北武穴人，硕士研究生，主要研究方向为复杂系统、可解释学习．

摘  要：为降低调频连续波（FMCW）雷达成本，同时提高定位精度，设计可解释解耦表征模型。该模型由网络解算器、虚假信号生成器以及可解释潜变量三部分组成。首先处理雷达信号获得中频频谱；然后输入到网络解算器中生成位置潜变量；再通过物理机制对潜变量进行转换，生成虚假中频信号频谱；最后，设计局部光滑损失函数对模型进行自监督训练，实现潜变量的解耦物理表征。实验结果表明：所提算法能对雷达系统频谱信号的粗粒度进行超分辨率细化，其机理能有效应对雷达系统的硬件公差、环境噪声、安装误差等问题，并可自动地训练出雷达的解算网络，从而具有大规模室内、机载联网定位的应用潜力。

关键词：调频连续波雷达定位； 可解释深度网络； 自监督学习； 超分辨率细化

中图分类号：TP183    文献标志码：A

文章编号：1001-3695（2024）02-037-0563-06

doi：10.19734/j.issn.1001-3695.2023.06.0269

Low-cost radar localization solution based on interpretable network

decoupling representation

Liu Leia，b， Lin Jiea

（a.School of Management， b.School of Optical-Electrical， University of Shanghai for Science & Technology， Shanghai 200093， China）

Abstract：In order to reduce the cost of frequency modulated continuous wave（FMCW） radar， while improving the positioning accuracy，this paper designed an interpretable decoupled characterization model. This model consisted of a network solver， a fake signal generator and interpretable latent variables. Firstly， it processed the radar signal to obtain the intermediate frequency spectrum. Then，it input processed signal into the network solver to generate position latent variables. Furthermore， it transformed these latent variables through physical mechanisms to produce a fake intermediate frequency spectrum. Finally，it designed a local smooth loss function to conduct self-supervised training on the model， achieving the decoupled physical representation of latent variables. Experimental results show that the proposed method can perform super-resolution refinement on the coarse spectrum signals of the radar system. The method can effectively addresses hardware tolerances， environmental noise， installation errors and other issues in the radar system. Moreover， it can train the radars solver network relatively automatically， demonstrating the application potentials for large-scale indoor and airborne network positioning.

Key words：frequency modulated continuous wave radar positioning; interpretable deep network; self-supervised learning; super-resolution refinement

0  引言

当今定位技术蓬勃发展，从惠及全球的卫星定位，到本地安装的机载测量，不同层级的定位技术正全方位地赋能工农生产、军事国防、智能交通、家居服务等领域的发展。受限于信号强度影响，卫星定位方法无法应用在室内、涵道、桥梁以及局部遮挡的高精度定位场景，所以亟需发展低成本的室内、机载局部定位技术，以满足当前人工智能爆发背景下的自动化需求。目前主流的局部定位技术包括机器视觉、无线网络、激光扫描、红外超声以及超宽带定位技术等，这些方法各具优缺点：机器视觉技术易受环境光源影响、对机器算力要求也较高［1］；无线网络、蓝牙定位这类方法较为复杂，精度还不甚理想［2］；激光雷达虽然精度较好，但成本较高［3］；红外超声虽然成本低廉，但是测量范围较小、精度较差，还难以满足精细定位需求［4］，与前述技术相比，调频连续波（frequency-modulated continuous-wave，FMCW）雷达具有体积小、成本低、精度高、盲区少、性能稳定等特点，所以在局部高精度探测领域具有较为独特的技术优势，该技术可通过接收连续调频信号的反射回波来测量反射物体的距离、角度，然后推算出反射物的位置，在雷达定位领域具有较为广阔的应用前景。随着自动技术的高速发展，对小体积、低成本、轻量化的雷达传感器需求日益迫切，但是现有的雷达精度还普遍较低，逐渐成为该领域发展的瓶颈，精度取决于雷达的设计布局与解算方法，如探测距离分辨率与发射信号的带宽成正比；探测角度分辨率与天线孔径值和通道数有关［5］，受限于雷达成本与安装尺寸，机载雷达的精度普遍在分米级［6］。为提升雷达系统的精度，一系列高分辨率算法随之被陆续提出，如多普勒雷达［7］、多频带雷达［7］、正交频分复用等［6］，这些方法可将系统精度提升到厘米级别，但代价是需要较大规模的天线阵列来满足低信噪比要求或者依赖于较精确的先验参数信息以及较复杂的数字信号处理技术等［8］。

可见传统的FMCW雷达技术的主要问题在于接收信息需专业人员开发较为复杂的逆向解算方法才能求獲取目标物体的真实位置，这需要较为资深的专业人员长期调试、标定才能完成特定需求的雷达开发，导致研发的人力成本较高。

当前以深度学习为代表的人工智能技术正蓬勃发展，深度学习在雷达定位方面也逐步开始应用。例如，文献［9］采用循环神经网络（recurrent neural network，RNN）实现了较高精度的定位解析；文献［10］使用卷积神经网络（convolutional neural network，CNN）对雷达图像进行特征提取和分类，但是由于神经网络具有黑箱特性，所以网络机理不具可解释性。如果利用人工智能方法来自动地完成低成本雷达的高精度可解释定位解算，则有助于推动机载雷达技术的应用推广，因此本文初步设计了一种基于可解释深度网络的自动解耦表征模型来获取被测物体的实际位置。该方法较全面地借助了雷达信号的生成机理，针对低成本雷达的生成噪声问题，有目的地设计平滑损失函数，用以自动优化所产生的虚拟雷达信号，从而实现了自监督的网络训练方法，物理解耦出目标物体的真实位置，该方法同时还能滤除雷达天线接收信号的各种随机噪声，最终实现较高精度的雷达信号解算。

1  调频连续波雷达的基本原理

考虑如图1（a）所示的FMCW雷达，天线阵列的间距为L，其中天线位置用蓝色圆孔表示（见电子版），以天线阵列中心为原点，阵列所在直线为x轴，构建雷达测量坐标系，设目标物体O到中心的距离为r，其与y轴的夹角为θ，则被测物体O的测量坐标X、Y可由下式计算：

X=r sin θ（1）

Y=r cos θ（2）

FMCW雷达通常采用各发射天线的双波回程距离来融合推算目标物体的测量位置O（X，Y），获取双波回程距离的具体方法为：FMCW雷达天线周期性地发射线性增长频率的连续波，然后接收反射信号进行混频，具体电路模块如图1（b）所示，其中第k条天线发射的单扫频信号可表示为

sTXk（t）=ATXkcos［2π（f0t+γt22）+0］  t∈［0，Tc］（3）

其中：幅值ATXk与发射功率有关；f0为载频；γ=B/Tc为调频斜率，B为扫频信号带宽；Tc为扫频周期时宽。则FMCW雷达单扫频周期内的发射信号相位模型可表示成

p（t）=2π（f0t+γt22）+0  t∈［0，Tc］（4）

考虑图1（a）所示的雷达坐标系，假设共有K根天线构成阵列，其中第k根天线的相对坐标为

Xk=-L2+（k-1）LK-1Yk=0  k=1，2，…，K（5）

则第k根天线的双程回波距离为

Rk=2（Xk-X）2+（Yk-Y）2  k=1，2，…，K（6）

由式（4）可得单扫频周期Tc内的雷达发射信号频率变化式为

f（t）=f0+γt  0≤t≤Tc（7）

则发射波信号可改写为

sTXk（t）=ATXkej2π（f0t+γ2t2）+0  0≤t≤Tc（8）

发射信号经过目标反射后被重新到达天线形成接收信号［11］，由式（6）可计算第k根天线的双程回波距离为Rk，则接收信号为

sRXk（t）=ARXkej2π（f0（t-τk）+γ2（t-τk）2）+0  τk≤t≤Tc（9）

τk=2Rk/c（10）

其中：幅值ARXk与接收信号强度有关；τk为接收时延；c表示光速。由于发射信号和接收信号在［τk，Tc］时间上有重叠，所以同时将这两组信号输入图1（b）所示的混频器中，即可得到中频信号（intermediate frequency signals，IF）：

sIFk（t）=sTXk（t）sRXk（t）=ATXkARXke［j2π（f0t+γ2t2）+0］-［j2π（f0（t-τk）+γ2（t-τk）2）+0］=ATXkARXkej2π（γτkt+f0τk-πγτ2k）  τk≤t≤Tc（11）

其中：第k根天线的发射信号相位pTXk（t）和回波信号相位pRXk（t）的差值表达式为

pTXk（t）-pRXk（t）=［2π（f0t+γt22）+0］-

{2π［f0（t-τk）+γ（t-τk）22］+0}=

2πf0τk+2πγτkt-πγτ2k（12）

由于τk1，则可忽略根据式（12）中的高阶小量τ2k。因为扫频信号具有线性增长特性，所以中频信号频率fIFk的具体计算方法可简化为

fIFk=γτk=γRkc=BRkcTc（13）

故双程回波距离Rk可被雷达测量的中频信号fIFk还原为

Rk=c2γfIFk（14）

多天线从不同角度对目标物体测距可进一步地用于目标定位，可见中频信号的处理方法对FMCW雷达的测量起到了至关重要的作用。传统方法是对中频信号进行数模转换采样，然后利用快速傅里叶变换（FFT）提取信号频谱来计算中频信号fIFk的具体值。由于采集信号长度有限，需要使用窗函数截取来减少FFT泄露误差，一般采用海明窗公式进行信号截断：

ω（n）=a0-（1-a0）cos（2πnN）  0≤n≤N（15）

其中：n为FFT频谱对应的频点索引；N为模数转换后的信号点数。则传统还原距离的方法式（14）可被进一步化简为

Rk=cTcfIFk2B=c2B×TcFsNnk=ΔR×nk（16）

其中：Fs为数模转换器的采样频率，有条件TcFs/N=1成立；ΔR=c/2B为雷达的距离分辨率，则利用FFT谱峰对应的频点索引nk即可还原反射物体到第k根雷达天线的距离。注意由于受到扫频带宽、采样频率以及信号截断等因素影响，雷达的分辨率一般较低。多个天线同时测距可进一步还原目标位置，设天线阵列的各自位置为Ok（Xk，Yk），则其到被测目标O（X，Y）的距离rk=Rk/2满足

（Xk-X）2+（Yk-Y）2=r2k（17）

对式（17）进行展开可得

X2+Y2+X2k+Y2k-2XXk-2YYk=r2k（18）

令Dk=X2k+Y2k，C=X2+Y2，则r2k-Dk=-2XXk-2YY+C，式（18）可改写为

r21-D1r22-D2r2K-DK=-2X1-2Y11-2X2-2Y21-2XK-2YK1XYC（19）

式（19）可进一步简写成m=An，其中m的元素为r2k-Dk，k∈［1，K］组成的已知列向量；A为系数矩阵；n为待求向量［X  Y  C］T。则可利用最小二乘法对式（19）进行计算，可解未知向量n为

n=（ATA）-1ATm（20）

由上述FMCW雷达系统测量基本原理可知：雷达精度会受到各种干扰影响，包括分辨率大小、分线性强弱、器件公差、测量噪声、规约误差等［12］，这些干扰会在系统中积累，最后造成测量位置发生较大偏离。虽然已有较多研究对雷达的精度改进提出了各种方案：如用已标定目标的雷达数据来分析定位误差来源，然后应用校正算法来消除误差［13］；或使用多项式模型来描述传送和接收信号之间的关系来校正FMCW信号的非线性［14］；抑或是通过使用更高质量的振荡器、更快的采样频率来生成高精雷达信号［15］；也有使用更先进的信号处理技术，如Kalman滤波来减少相位噪声［16］。但是这些方法都需要较专业的工程人员来进行精细设计和长时间调整才能获得较高的雷达精度，所以能否借助可解释深度学习技术来较为简单地自动计算目标物体的位置，并能较方便地优化雷达精度则成为该领域亟需解决的重要问题。

2  基于可解释深度网络的位置解算方法

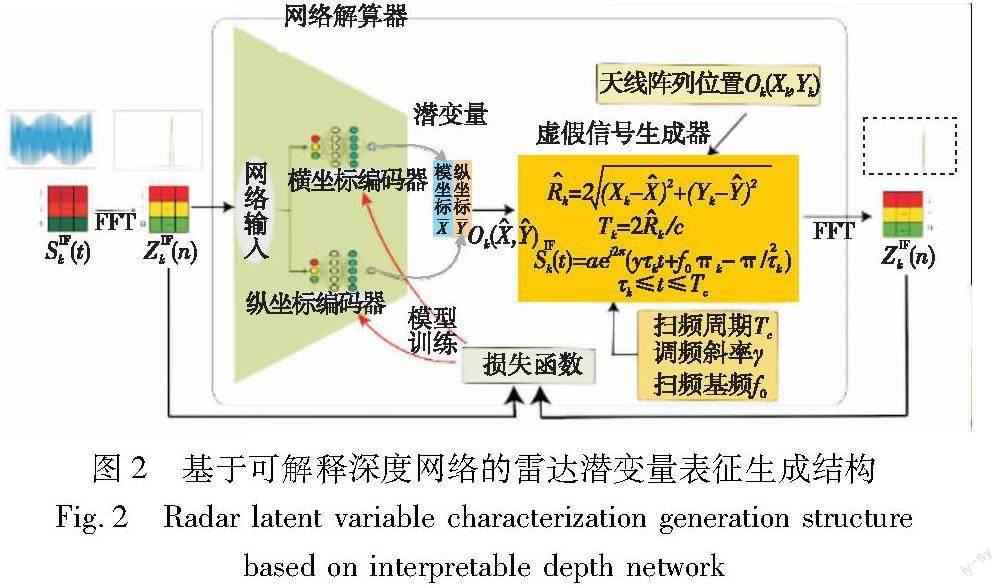
传统解算方法需要根据各天线的中频信号频谱获取各自双程回波距离，接着进一步推算物体位置，如果雷达阵列天线过少，天线的间距又过小，则解算精度会大幅降低，如果采用较多天线和较宽间距，则会导致雷达成本过高、尺寸过大，不利于紧凑安装要求，为此提出一种基于可解释深度网络的潜变量解耦表征模型，用于稀疏天线阵列的紧凑雷达高精度测量。

设计如图2所示的深度網络解耦表征模型，该模型包括网络解算器、虚假信号生成器和可解释潜变量三部分。

一般而言，深度网络解算器生成的潜变量不具备可解释性，多作为显变量的组合映射。究其原因在于在解算网络训练时无法有效引导潜变量向真实物理变量收敛，并且潜在变量之间存在较严重的相互耦合，从而造成解算网络的解耦表征效果不佳。为将潜变量还原成目标的真实位置，使内部的潜变量具有物理可解释性，专门设计两个独立的解算网络来整合所有的雷达天线数据，该网络的输出为目标物体的位置估计（X^，Y^），然后利用雷达基本原理作为虚假信号生成器来生成虚假雷达信号，最终形成自监督学习的网络框架。该网络模型的训练原理为：提高雷达各天线输出的真实信号与所生成的虚假信号之间的相似程度，由于虚假信号生成器模拟了真实物体信号的雷达处理电路，所以网络生成的潜在估计变量只有逼近真实的目标位置，才能满足网络训练的损失函数优化要求，这样就能保证潜变量具有真正的物理可解释性。

2.1  深度网络解算器设计

图2所示深度网络模型的解算器用于融合各天线的中频信号频谱，目的是通过训练直接高速映射出具有物理含义的潜变量位置估计，可直接替代传统几何方法的还原式（16）～（20），在充分训练后可以高速估计出被测物体的真实位置。该网络使用大量数据进行自监督训练，可以自动地通过优化训练滤除雷达测量环节中的安装误差、器件质量、重复精度等问题的影响。解算器结构采用全连接网络形式，其输入层承接雷达各天线中频信号的FFT处理数据Zk（n）（n=1，2，…，N；k=1，2，…，K）其中N表示雷达中频信号的频谱点数，K表征雷达的天线个数，将各天线数据按顺序串行排列，输入总维度为K×N，为保证解耦潜变量的横、纵坐标（X^，Y^）独立性，有针对性地设计了两个同构网络来分别生成单一位置估计，具体网络层维度参数为［K×N，512，1024，512，256，1］，其中输入层K×N个神经元代表全部K个天线的所有FFT信号点数，解算器输出层的1个神经元代表要生成的独立潜变量位置估计，为保证较为良好的梯度优化质量，解算器各层之间使用Mish激活函数y=x·tanh（ln（1+ex）），该激活函数具有类ReLU函数的优点，既保证较深的梯度传播，又具有绝佳的平滑性，有利于深度求导计算，适宜应对自动化可解释网络的建模问题。

2.2  基于雷达机理的虚假信号生成器

对于给定雷达系统，天线位置Ok（Xk，Yk）（k=1，2，…，K）、扫频周期Tc、调频斜率γ、扫频基频f0等参数属于雷达的设计信息，可作为已知量嵌入到虚假信号生成器中，这样便能使用机理公式来模拟雷达信号的实际处理电路，从而仿造出虚假的中频信号，以便后续利用网络模型训练自动地实现潜变量的超分辨率定位。将雷达K个天线位置Ok（Xk，Yk）和潜变量位置估计O^（X^，Y^）代入式（6），则可生成K个双程回波距离估计：

R^k（t）=2×（Xk-X^）2-（Yk-Y^）2  k=1，2，…，K（21）

接着根据式（11）（12）计算K个天线接收信号的中频相角估计k：

k（t）=2×π×γ×Tc×R^k×tc+2×π×f0×R^kck=1，2，…，K（22）

由于本文的主要目的是探索可解释网络超分辨率解算FCMW雷达信号的可行性，所以采用固定反射率的仿真物体进行实验，代入式（11）可得S^IFk=×sin（k（t）），从而能获得雷达各天线的虚假信号输出S^IFk，k=1，2，…，K，用FFT处理虚假信号即可获得与可解释网络输入一致的各天线虚拟频谱数据Z^k（n）（n=1，2，…，N，k=1，2，…，K），其中N为频谱点数。具体伪代码如算法1所示。

算法1  虚假信号生成器伪代码

输入：潜变量位置估计坐标O^（X^，Y^）；雷达天线位置Ok（Xk，Yk）（k=1，2，…，K）。

输出：各天线的虚拟中频信号频谱Z^k（n）（n=1，2，…，N;k=1，2，…，K）。

t=1：Tc/Ts  //时间序列索引数组

for k=1：K  //对每个天线计算中频频谱

R（k）=2×［sqrt（X^-Xk）×^2 +（Y^-Yk）×^2］

//第k天线到潜变量位置距离

P（k）=2×π×γ×Ts×t×R（k）/c+2×π×f0×R（k）/c

//第k天线接收信号相位

S（k）=×sin（P（k））  //第k天线的接收信号

对S（k）进行FFT给出中频信号频谱Z^k（n）（n=1，2，…，N；k=1，2，…，K）

end

2.3  自监督学习的损失函数设计

虽然传统定位方法式（20）不具备高精度定位能力，但可以大致预估出被检测物体的近似位置，尤其是在少量天线参与测量的情况下，传统定位方法可以高速地解算出大致目标位置（，），在此基础上则能利用所提可解释网络模型进一步地提升位置估计精度。具体做法是在传统方法预估位置处（，）设定一个边长为2R的矩形区域，将网络估计的潜在变量位置通过损失函数限定在该区域，以作为启发来保证网络训练的快速收敛，所以设计如下的损失函数：

l1=W1×［max（0，-R）+max（0，R-）］（23）

其中：W1为l1损失函数的权重，式（23）主要用来启发潜变量X^坐标的搜索方向，即网络估计横坐标X^与方程粗略解算横坐标的距离小于R时不作惩罚，而距离超出R的部分会按W1权重计算损失，目的是利用稀疏天线粗略的传统解算结果来训练更加精准的网络解算器；与潜变量横坐标启发类似，潜变量纵坐标估计Y^也具有形式的损失函数l2：

l2=W1×（max（0，Y^-R）+max（0，R-Y^））（24）

为保证潜变量位置估计能向目标的实际位置收敛，就必须借助虚假信号生成器，如果能构建虚假信号与真实信号的相似性增强闭环，则潜在变量便会自动地收敛于真实目标位置。根据上述原理，网络模型生成的虚假中频信号频谱Z^k（n）（n=1，2，…，N；k=1，2，…，K）要与雷达输出的真实中频信号频谱一致。为减少训练过程中显存占用，提升显卡CUDA单元的运算效率，分别提取了真实信号与虚假信号频谱数组的峰值索引IZmaxk，I^Zmaxk，则真实信号与虚假信号的相似损失可被简化为

l3=W2K∑Kk=1（IZmaxk-I^Zmaxk）2（25）

其中：W2为损失权重。综合上述损失函数设计，最终用于可解释网络训练的损失函数为

l=l1+l2+l3（26）

3  基于可解释网络模型的仿真实验

3.1  仿真实验设计及模型设定

使用LabVIEW编写仿真程序，通过仿真程序模拟位置为O（X，Y）目标物体，根据式（1）～（10）计算出FMCW雷达各天线的接收信号，并添加白噪声存储成数据文件，为降低雷达成本与安装尺寸，采用稀疏天线阵列设计，天线数被设计成了K=3个，期望所提可解释网络方法能通过自学习获取较精确的位置潜变量估计，雷达仿真程序与可解释网络模型的设计参数如表1所示。

为测试所提深度模型有效性，先利用仿真程序模拟单目标位置产生的雷达信号训练网络，观察潜变量的收敛效果，其中可解释深度网络采用PyTorch编写，训练主机使用DellT630服务器，配置NVIDIA GeForce RTX 3080 GPU，训练采用批量梯度下降策略，并且使用AdamW优化器最小化损失函数，初始学习率设置为5E-5，权重衰减设为0.000 5，为减少过拟合，早停法实验定50轮停止。

实验结果如图3（a）所示，仿真程序模拟的目标位置在（3，4），如图中红色十字标记位置（见电子版），通过多次训练，证明系统的潜变量估计无法向真实位置收敛。图3（a）顯示了某次训练结果，每轮训练潜变量的位置估计使用蓝青色散点表示，颜色由浅入深依次表征了网络在不同训练轮次的潜变量估计，该图表明，除去初始几轮训练的潜变量可以在位置空间内搜寻最小损失点，之后的大部分时间会逐渐被困在某些位置无法继续寻优。深入分析原因发现：这是由于在训练后期，一般的网络学习算法会大幅衰减学习率以提升系统精度，但该操作会导致所设计的损失函数式（26）无法计算有效梯度。通过对图中x=3虚线位置的中频信号计算频谱峰值索引损失式（25），发现该损失函数确实在目标点y=4处的损失最小，如图4绿色曲线所示，但是通过对该损失函数曲线最优位置放大发现，由于数字频谱不连续，所以损失函数在微观层面表现为阶梯变化，随着网络训练的轮数加深，必然造成深度优化器在小学习率优化过程中产生梯度为零的情况，从而丧失网络训练优化动力，导致潜变量向目标位置的收敛运动停滞。

3.2  损失函数的平滑性改进

原始损失函数式（25）具有阶梯化特性，这也是造成传统解算方法精度过低的根本原因，如何对损失函数进行改造？如图4红色虚曲线，使可解释网络能生成出超过原有系统分辨率限制的位置估计，将是低成本、高紧凑性FMCW雷达设计的关键。针对原损失函数特点，采用平滑化处理技术来解决网络训练的梯度消失问题，函数的局部平滑化方法通常是在自变量周围多点采样因变量数值，然后利用统计、插值、回归、机器学习等方法来实现函数局部的多点平滑预估，如图4红色虚线所示，其可将原始的阶梯函数局部平滑为光滑曲线，有利于网络训练中的函数求导。

考虑以可解释深度网络生成的潜变量位置估计O^（X^，Y^）为中心，边长为L的矩形邻域内均匀生成的S2个重采样点，这些点的横纵坐标为

X^ij=X^-L2+i×LS（27）

Y^ij=Y^-L2+j×LS（28）

其中：i，j=1，2，…，S。则可分别通过虚假信号生成器与式（25）来共同计算出每个重采样点O^ij（X^ij，Y^ij）相对真实频谱峰值索引IZmaxk的损失函数lij。为提升平滑计算速度，潜变量位置估计O^（X^，Y^）的损失函数可以用其邻域重采样点的损失均值代替：

ls=1S2∑Si∑Sjlij（29）

从而利用了潜变量估计的局部空间损失平滑了原始损失函数式（25），则最终的训练损失为

l=l1+l2+ls（30）

具体伪代码计算过程如算法2所示。

算法2  损失函数平滑化算法

输入：潜变量坐标估计O^（X^，Y^）；作为训练标签的各天线仿真中频信号频谱Zk（n）（n=1，2，…，N;k=1，2，…，K）；邻域单边采样点数S；邻域单边长度L。

输出：平滑损失函数值ls。

for i = 1：S  //生成重采样点的行标号

for j = 1：S  //生成重采样点的列标号

X^ij=X^-L2+i×LS  //O^邻域重采样点横坐标

Y^ij=Y^-L2+j×LS  //O^邻域重采样点纵坐标

for k=1：K  //对每个天线进行操作

利用算法1计算k天线的中频信号频谱Z^kij（n）（n=1，2，…，N;k=1，2，…，K）

［～，I^kmaxijI］=sort（Z^kij（n））  /*找出重采样点生成的中频信号频谱的最大索引*/

［～，ImaxkI］=sort（Zk（n））  /*找出实际物体生成的中频信号频谱的最大索引*/

end

利用式（25） 处理kmaxij和Imaxk，得出各重采样点的损失lij

end

end

利用式（30）计算所有lij的均值作为平滑损失输出ls

3.3  光滑损失函数的网络训练结果分析

对损失函数的光滑化性改造可以有效推进可解释网络潜变量向真实物理位置收敛，如图3（b）所示，分别实验（-4，3）、（3，4）两点作为真实目标位置，对两点分别进行独立网络训练，以观测潜变量在每轮训练过程中的收敛过程，该图表明，随着迭代次数的提升，所提解算器可以较精确地收敛于真实目标位置。为评估所提深度网络模型的解析精度，对雷达前方横坐标-7～+7m ，纵坐标0～7m的矩形区域均匀仿真1 000点进行精度评估，绘制测量误差的热力图，如图5所示，其中典型仿真坐标位置估算误差数据如表2所示。图5中蓝色区域为误差较小的部分（见电子版），红色区域则误差较大，该图表明，雷达正前方或者距离较近的位置误差较小，两侧的误差较大，并且精度数值不具备轴线对称性，这是由雷达天线排布、损失函数特性以及训练随机过程决定的。

图5范围内的仿真点位置平均估计误差为0.0875±0.0012 m，得益于所设计的平滑损失方法，使得在仅使用三孔径天线的简单电路就能在粗粒度中频信号频谱下还原出超分辨率定位的结果。

表2列举了部分主流雷达定位方法的精度，在相对硬件成本较低的情况下，所提可解释网络解析方法具有较高的位置估计精度。对比文献［9，17］定位方法可以得出：相对于Wi-Fi深度网络定位，使用FMCW雷达技术可以获得更高的定位精度。文献［17］的FMCW定位精度为0.177 m，同样是使用FMCW技术，所提可解释网络解析方法相比WiTrack精度有较大幅度提升，并且雷达天线布置比WiTrack系统更加紧凑；另一方面，文献［18］提出了一种交叉定位雷达系统，该系统结合了两种不同频率的雷达，以实现更加准确和稳定的目标定位，定位精度可达0.154 5 m，但仍旧难以达到超分辨率测量；此外，红外定位系统虽然价格低廉，但是无法保证测量精度，即使采用昂贵的红外成像技术［19］，并融合了可见光和红外双重信号源，精度也仅能达到0.3 m，较难应对自动化环境中的精准定位需求。文獻［20］是基于FMCW雷达技术的主流定位方法最大恒虚警率（greatest of-constant false alarm rate，GO-CFAR），可有效地提高定位精度和抗干扰能力，该系统的定位精度能到达0.123 m，与本文方法相比，还具略有不足；文献［21］介绍了一种基于超宽带定位技术的系统，该系统结合了范围单元平衡（range-cell-leveling，RCL）算法和到达角（angle of arrival，AOA）算法，可以实现更加精确和稳定的目标定位，该系统的定位精度为0.105 m，研发难度较高。

综上所述，不同定位方法各具特点，其定位精度也存在较大差异。基于所提可解释网络的FMCW雷达技术具有较高精度，天线布局更紧凑，硬件成本更低廉，配合专用的神经网络解算芯片，雷达外形更加便携，所以在室内环境、车载布置方面具有较大规模组网应用的潜力。

4  结束语

所提基于可解释网络解耦表征定位的FMCW雷达方法能利用自监督学习框架自动地精准解析，该网络借助虚假信号生成器的物理机理，帮助解码器生成符合物理位置估计的潜在变量，并且针对雷达系统频谱信号的粗粒度，设计了局部光滑化的损失函数用于训练网络，使得针对廉价硬件基础的复杂网络训练成为可能。在这种学习框架下的网络解算器能有效融合雷达系统的硬件信息、环境噪声信息、安装误差信息，借助网络学习过程自动地标定雷达参数，该过程无须复杂参数调整，对安装人员友好，无须高素质的研发人员配合，适于大批量的室内定位应用，例如地下停车场、公共图书馆以及博物馆、大型商场等固定安装环境。

作为低成本FMCW雷达的可解释深度网络解析初探，对于动态、多目标复杂场景的网络解析研究还需要进一步对网络结构进行改进，例如在网络中嵌入多目标物理模型；或者嵌入系统动力学模型来实现动态系统跟踪与多目标系统解析；或者结合其他传感器来进一步提高定位精度和可靠性。因此，下一步将考虑如何将所提低成本可解释网络方法应用于多目标场景的运动目标定位问题，以进一步落地智能制造、无人驾驶、智能家居、垂直农业等实际应用领域。

参考文献：

［1］Kim S B， Bazin J C， Lee H K， et al. Ground vehicle navigation in harsh urban conditions by integrating inertial navigation system， global positioning system， odometer and vision data［J］. IET Radar， Sonar & Navigation， 2011，5（8）： 814-823.

［2］Fernández-Caramés T M， Fraga-Lamas P， Suárez-Albela M， et al. A fog computing based cyber-physical system for the automation of pipe-related tasks in the industry 4. 0 shipyard［J］. Sensors， 2018，18（6）：1961-1968.

［3］Feng Daquan， Wang Chunqi， He Chunlong， et al. Kalman-filter-based integration of IMU and UWB for high-accuracy indoor positioning and navigation［J］. IEEE Internet of Things Journal， 2020，7（4）： 3133-3146.

［4］Gualda D， Pérez-Rubio M C， Urea J， et al. LOCATE-US： indoor positioning for mobile devices using encoded ultrasonic signals， inertial sensors and graph-matching［J］. Sensors， 2021，21（6）：1950.

［5］Han K， Hong S. High-resolution phased-subarray MIMO radar with grating lobe cancellation technique［J］. IEEE Trans on Microwave Theory and Techniques， 2022，70（5）： 2775-2785.

［6］蒋留兵， 潘波， 吴岷洋， 等. 基于FT_SSIM和ICAGA_CNN在小样本场景下雷达动作识别方法研究［J］. 计算机应用研究， 2022，39（4）： 1105-1110. （Jiang Liubing， Pan Bo， Wu Minyang， et al. Research on radar action recognition method based on FT_SSIM and ICAGA_CNN in small sample scenarios［J］. Application Research of Computers， 2022，39（4）： 1105-1110.）

［7］Meng Zhen， Fu Song， Yan Jie， et al. Gait recognition for co-existing multiple people using millimeter wave sensing［C］//Proc of AAAI Conference on Artificial Intelligence. 2020： 849-856.

［8］Xu Xiaofei， Nie Zhixi， Wang Zhenjie， et al. Performance assessment of BDS-3 PPP-B2b/INS loosely coupled integration［J］. Remote Sensing， 2022，14（13）： 2957.

［9］Panwar K， Katwe M， Babu P， et al. A majorization-minimization algorithm for hybrid TOA-RSS based localization in NLOS environment［J］. IEEE Communications Letters， 2022，26（5）： 1017-1021.

［10］陳立福， 武鸿， 崔先亮， 等. 基于CNN的SAR图像目标和场景分类算法［J］. 雷达科学与技术， 2018，16（6）： 627-632. （Chen Lifu， Wu Hong， Cui Xianliang， et al. CNN-based algorithm for SAR image target and scene classification［J］. Radar Science and Technology， 2018，16（6）： 627-632.）

［11］陈春利， 金炜东. 一种改进的DNN算法在雷达信号分选中的应用［J］. 计算机应用研究， 2019，36（4）： 1178-1180，1185. （Chen Chunli， Jin Weidong. Application of an improved DNN algorithm in radar signal classification［J］. Application Research of Compu-ters， 2019，36（4）： 1178-1180，1185.）

［12］王泓霖， 李偉， 许强， 等. 基于深度置信网络的高分辨率雷达距离像识别［J］. 计算机应用研究， 2020，37（3）： 872-875. （Wang Honglin， Li Wei， Xu Qiang， et al.High-resolution radar range profile recognition based on deep belief network［J］. Application Research of Computers， 2020，37（3）： 872-875.）

［13］Zhang Nae， Sun Yang， Li Yuxiang， et al. Joint resource allocation scheme for target tracking in distributed MIMO radar systems［J］. Journal of Systems Engineering and Electronics， 2019，30（4）： 709-719.

［14］Ke Junchen， Dai Junyan， Zhang Junwei， et al. Frequency-modulated continuous waves controlled by space-time-coding metasurface with nonlinearly periodic phases［J］. Light： Science & Applications， 2022，11（1）： article No.273.

［15］Yan Kai， Zhang Yue， Pan Shengsen，et al. Design and implementation of real-time extraction software for direct wave parameters［C］//Proc of the 2nd IEEE Advanced Information Management， Communicates， Electronic and Automation Control Conference. Piscataway，NJ：IEEE Press， 2018： 261-265.

［16］Sheng Danting， Mingrui H. Research on multi-vehicle positioning technology based on Kalman filter algorithm［C］//Proc of International Conference on Autonomous Unmanned Systems. Singapore： Springer， 2023： 687-697.

［17］Adib F， Kabelac Z， Katabi D， et al. 3D tracking via body radio reflections［C］//Proc of USENIX Conference on Networked Systems Design and Implementation. 2014： 317-329.

［18］Nweke H F， Teh Y W， Mujtaba G， et al. Multi-sensor fusion based on multiple classifier systems for human activity identification［J］. Humancentric Computing and Information Sciences， 2019，9： 1-44.

［19］Huang Baoqi， Xie Lihua， Yang Zai. TDOA-based source localization with distance-dependent noises［J］. IEEE Trans on Wireless Communications， 201，14（1）： 468-480.

［20］林佳慧， 尹辉斌， 熊荣鹏. 基于FMCW雷达传感器的室内人员定位方法［J］. 传感器与微系统， 2021，40（11）： 50-53. （Lin Jiahui， Yin Huibin， Xiong Rongpeng. Indoor personnel localization method based on FMCW radar sensor［J］. Sensors and Microsystems， 2021，40（11）： 50-53.）

［21］Bottigliero S， Milanesio D， Saccani M， et al. A low-cost indoor real-time locating system based on TDOA estimation of UWB pulse sequences［J］. IEEE Trans on Instrumentation and Measurement， 2021，70： article No. 5502211.