基于模糊故障树的某高炮无线电引信安全评估

贺 玮,李 波,麻旭东

(1.中北大学 机电工程学院, 太原 030051; 2.中国人民解放军61767部队)

0 引言

引信作为弹药的控制系统,其安全性历来被设计、研制和使用部门所重视[1]。引信安全性是整个武器系统的重要性能和关键技术指标之一,是衡量引信的设计特性,判定引信的使用特性以及引信的战术、技术指标的重要依据。引信安全性还与引信的生产制造、使用保障因素密切相关。因此,须采取相应的保障措施,以求达到引信的可靠性要求[2]。

传统的机电引信故障树分析一般是基于Bell静态故障树逻辑门来进行可靠性评估。但随着可靠性技术的发展,人们意识到整个系统的失效分析并不能仅仅基于静态的逻辑门进行分析,如机电引信在经过长期贮藏,内部的电子元件、弹性元件、火工品等部件会发生部分性能退化,造成引信性能的下降,还有引信在工作过程中受到环境和软件故障的影响,这使得引信的安全性影响往往难以评估。并且传统机电引信故障树中事件发生具有时序性,底事件的概率值较为精确,对于精密复杂的引信系统,二元的故障描述状态并不能准确地描述引信系统的具体失效状态。鉴于此,谭正超等[3]提出了基于层次分析法的引信安全性评估方法,即通过设计准则满足情况作为切入点,建立基于设计准则的安全性评估模型,并应用层次化分析方法进行优化分析。但这种安全性评估方法未考虑实现安全系统的软、硬件的安全失效概率,仅关注了安全系统不同架构之间的优劣判断。

模糊故障树作为一种新进发展的故障树分析方法,它相对于Bell故障树,能够描述底事件与上级事件的模糊关系和复杂系统的多态、组合和顺序等事件关系[4]。在安全性分析应用上,宋华等人提出了模糊故障树分析方法,并对INS/GPS组合导航系统进行了实例分析[5]。姚成玉等人提出了模糊故障树的重要度概念及其计算方法,并用部件重要度分析方法进行算例对比与分析,验证方法的可行性[6]。刘勇等人将模糊故障树模型应用到多态导航系统性能分析中,求解系统在多故障状态下的性能可靠性指标,并进行了实例分析[7]。本文中根据现有的研究成果,结合模糊故障树基本理论,提出模糊故障树的构建和分析方法,并参考标准GJB z29A—2021《引信典型故障树手册》中的引信典型故障树实例,对引信的部分作用过程建立模糊故障树进行重要度分析和概率值计算,与传统的Bell静态故障树的分析计算进行对比,为引信的安全性优化和故障树诊断提供参考。

1 引信模糊故障树模型及计算方法

模糊故障树模型是基于学者Takagi等[8]提出的使用模糊含义和推理的系统模糊模型,通过可定义的逻辑规则来描述下级事件的状态对上级事件的影响。基于模糊故障树的引信安全性分析方法如图1所示,具体步骤如下:

1) 对引信系统进行分析,确定顶事件和底事件类型;

2) 构建逻辑门,描述规则和构建方法,确定中间事件类型;

3) 确定引信底事件的随机模型和可靠性数据;

4) 根据各事件代码来搭建引信模糊故障树;

5) 计算引信上级事件和顶事件概率值;

6) 对引信底事件进行重要度分析;

7) 进行引信安全性评估和故障树诊断。

图1 引信模糊故障树的构建和分析方法框图

1.1 引信模糊故障树上级事件概率值计算方法

一个简单的引信模糊故障树模型如图2所示,其中X1,X2,…,Xn为底事件,y为上级事件,S为一个可以定义规则的逻辑门。

图2 一个引信模糊故障树

若在规则l中,下级事件x=(x1,x2,…,xn)的各故障状态的概率值分别为

则S门描述规则的输入规则l(l=1,2,…,r)的执行可能性为

(1)

(2)

1.2 引信模糊故障树底事件重要度计算方法

重要度可以表示底事件概率值的变化对顶事件概率值的影响程度,对引信系统安全性评估和优化具有重要作用,本文中采用概率重要度和关键重要度进行分析。

1.2.1模糊故障树底事件概率重要度计算方法

模糊故障树概率重要度可以表示为

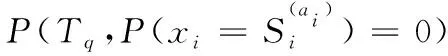
(3)

则基本事件xi对顶事件T故障状态为Tq的T-S故障树概率重要度为

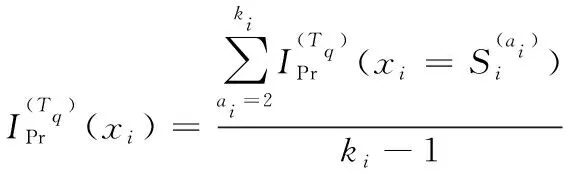
(4)

式(4)中:ki为底事件xi所有故障状态的个数,若故障状态为0、0.5、1,则ki=3。

1.2.2模糊故障树底事件关键重要度计算方法

模糊故障树关键重要度可以表示为

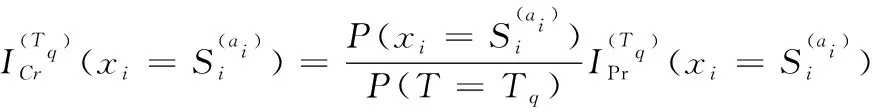
(5)

式(5)中:P(T=Tq)为顶事件T为Tq的概率值。

则基本事件xi对顶事件T故障状态为Tq的T-S故障树关键重要度为:

(6)

2 实例分析

本文中以GJB z29A—2021《引信典型故障树手册》中某小口径高炮无线电引信在预定的解除保险和接触隔离流程开始前引信作用故障树为例进行分析[9]。由于该故障树中存在概率相同的相似底事件,因此对该故障树和底事件进行简化。

建造如图3所示的故障树,记顶事件为T12,中间事件为A12、B12、C12、D12和T11,底事件为X1～X8,故障树事件代号、名称和发生概率如表1所示。

图3 某小口径高炮无线电引信在预定的解除保险和 接触隔离流程开始前引信作用故障树

表1 故障树事件代号、名称和发生概率

假设X3～X8、A12、B12、C12、D12和T11的故障状态为(0,0.5,1),其中0表示正常状态,0.5表示半故障状态,1表示失效状态,且故障状态为0.5的故障率与故障状态为1的相同。G1～G6为可定义规则的逻辑门,其中G1门规则见表2,G2和G5门规则见表3,G3和G4见表4和表5。由于G6门下B12先于A12发生,即B12事件的故障状态为0.5和1时A12事件才发生,如表6所示。在进行Bell故障树计算和分析时,G1、G3、G6为与门,G2、G4、G5为或门,底事件的概率值与表1相同。

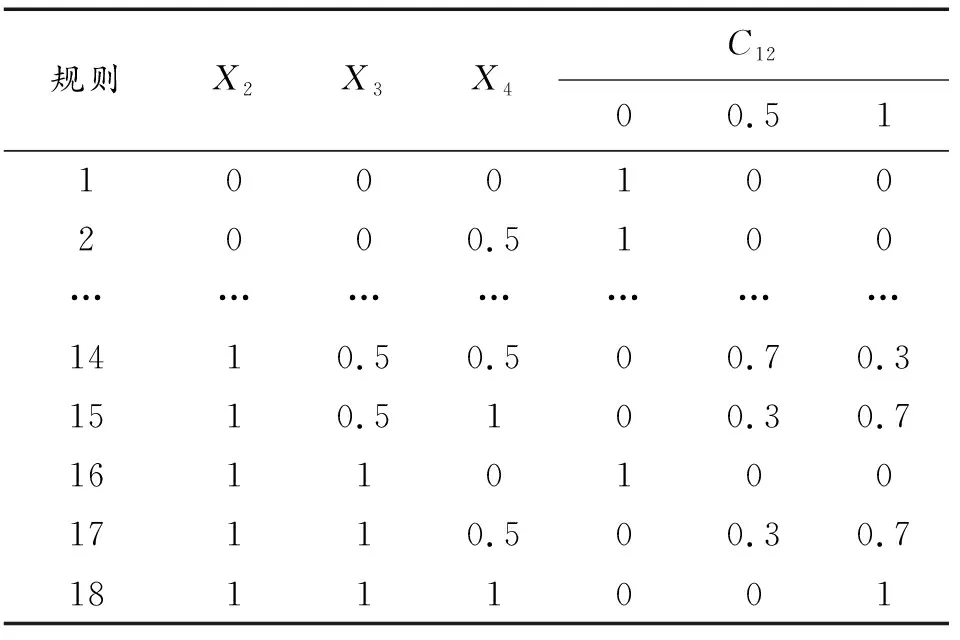
表2 G1门规则

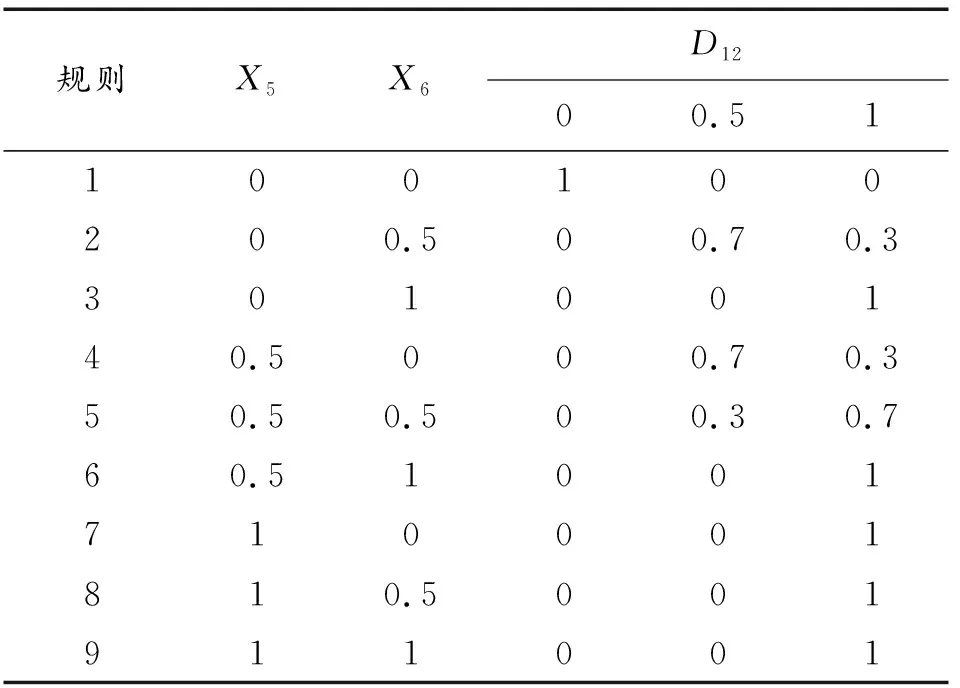
表3 G2和G5门规则

表4 G3门规则

续表(表4)

表5 G4门规则

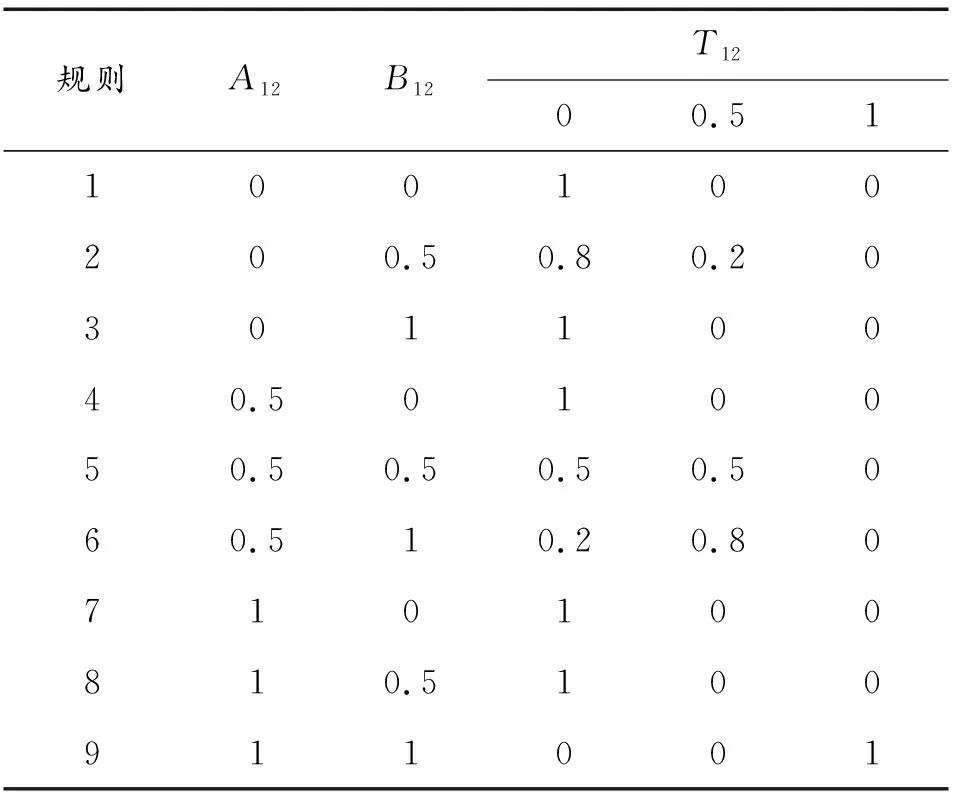
表6 G6门规则

2.1 计算引信故障树顶事件的概率值

2.1.1计算模糊故障树顶事件的概率

以中间事件D12为例根据G2门规则计算D12在故障状态为0、0.5和1时的概率值

同理,利用上述方法根据表1的故障概率值和表2—表6的规则,求得中间事件A11、B11、C11、T11和顶事件T12的故障状态为0、0.5、1的概率值如表7所示。

表7 中间事件和顶事件各故障状态概率值

由上述结果可得,失效事件和顶事件的无故障、半故障和失效状态的概率值之和为1。某引信小口径无线电引信在预定的解除保险和解除隔离流程开始前引信出现故障和半故障是一个小概率事件,该事件的概率值比底事件的概率值小4个数量级。而引信正常工作的可能性非常大,与实际的引信安全性分析一致,验证了本文中提出的模糊故障树在引信安全性评估上的可行性和准确性。其中,电雷管炸、在预定的解除保险和解除隔离流程开始前安全失效、安全系统原发性失效这3个中间事件发生的概率较其他事件高出几个数量级,因此,在该小口径无线电引信出现故障时需要重点关注这3部分的工作状况。

2.1.2计算Bell故障树顶事件的概率

首先用上行法求所有最小割集,将顶事件表示为各底事件积之和的最简布尔表达式[10],即

T12=X1X5+X1X6+X1X7X8+X2X3X4X5+X2X3X4X6+X2X3X4X7X8

根据不交布尔代数法将上式变为不交和,即

将表1的数据代入,并通过首项近似的方法,得顶事件概率值P(T12)≈1.2×10-9。

模糊故障树和Bell故障树计算所得的顶事件概率值处在同一数量级且比较接近,证明了模糊故障树计算方法的可行性和准确性。

在计算顶事件概率时,Bell故障树可以使用上行法快速得到结构函数,代入底事件的概率值计算得到顶事件的概率值。但在故障树较为复杂或底事件较多时,会发生“组合爆炸”问题,一般情况下可以采用首项近似的方法快速得到顶事件的概率值。而模糊故障树在计算时由于考虑有半故障的故障状态存在,在计算时较为繁琐,需要借助软件编程进行辅助计算。

2.2 计算引信故障树底事件的重要度

2.2.1计算模糊故障树底事件的概率重要度

根据式(3),底事件X8故障程度为0.5对顶事件T12故障状态为0.5的模糊故障树概率重要度为

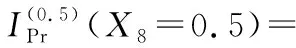
底事件X8故障程度为0.5对顶事件T12故障状态为1的模糊故障树概率重要度为

底事件X8故障程度为1对顶事件T12故障状态为0.5的模糊故障树概率重要度为

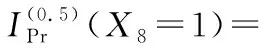
底事件X8故障程度为1对顶事件T12故障状态为1的模糊故障树概率重要度为

由式4即可计算底事件X8故障状态为0.5和1对顶事件T12的概率重要度分别为

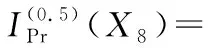
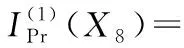
同理,可得各底事件对顶事件T11故障状态为0.5和1的模糊故障树概率重要度如表8所示。

表8 底事件对顶事件T11故障状态为0.5和1的 模糊故障树概率重要度

续表(表8)

2.2.2计算模糊故障树底事件的关键重要度

根据式(5),底事件X8故障程度为0.5和1对顶事件T12故障状态为0.5和1的模糊故障树关键重要度为

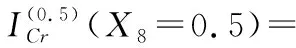
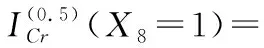
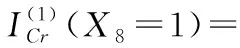
由式(6)即可计算底事件X8故障状态为0.5和1对顶事件T12的概率重要度分别为

同理,可得各底事件对顶事件T12故障状态为0.5和1的模糊故障树关键重要度如表9所示。

表9 底事件对顶事件T12故障状态为0.5和1的 模糊故障树关键重要度

由表8的模糊故障树概率重要度和表9的模糊故障树关键重要度可知,该小口径无线电引信在在预定的解除保险和解除隔离流程开始前,引信系统出现半故障时,X5,X7,X8,X6的关键重要度较大,设计中要对隔爆机构和保险机构进行重点优化,同时按照可X5,X7,X8,X6,X1,X2,X3,X4的顺序依次排查;引信系统出现失效故障时,X1,X5的关键重要度较大,提高电雷管和隔爆材料的性能对预防引信系统失效故障的效果明显,同时按照可X1,X5,X6,X7,X8,X2,X3,X4的顺序依次排查。

其中X2,X3,X4和X7,X8由于处于“与门”下,几个底事件对顶事件变化的影响较小。而在对故障树进行优化时,底事件X1对顶事件T概率值的影响最大,可以对X1进行优化设计,或者在顶事件下增加安全系统设计,从而提高引信的安全性。

2.2.3计算Bell故障树底事件的概率重要度

底事件的概率重要度表示第i个底事件的概率重要度,定义为

(7)

式(7)中:Q(q1,q2,…,qn)为顶事件发生的概率,在底事件相互独立的条件下,为各底事件发生概率q1,q2,…,qn的一个函数。

可求得在图3所示故障树的函数为

Q(q1,q2,…,qn)=q1q5+(1-q5)q1q6+ (1-q5)(1-q6)q1q7q8+(1-q1)q2q3q4q5+ (1-q1)(1-q5)q2q3q4q6+ (1-q1)(1-q5)(1-q6)q2q3q4q7q8

将表1的数据代入式(7),得底事件X1—X6的概率重要度如表10所示。

表10 Bell故障树底事件的概率重要度

2.2.4计算Bell故障树底事件的关键重要度

事件的关键重要度表示第i个底事件的相对概率重要度,定义为

仍将表1的数据代入式(8),得底事件X1—X6的关键重要度如表11所示。

表11 Bell故障树底事件的关键重要度

在计算底事件的重要度时,模糊故障树是通过对底事件的各故障状态的故障概率值赋1,计算出此时顶事件的概率值,并与底事件的完全无故障情况下顶事件的概率值做差进行计算的。由于在引信的故障树中,底事件的概率值很低,靠近顶事件的部分底事件在Bell故障树重要度计算结果中,要比其余底事件的重要度高出几个数量级,如表8—表11所示的情况。模糊故障树和Bell故障树的重要度计算结果基本都处于同一数量级下,证明了模糊故障树计算方法的可行性。

模糊故障树的重要度计算可以直观地显示底事件对顶事件各故障状态的重要程度,并且并不依赖于故障树结构函数的分析和运算,而是直接根据规则进行计算,降低了分析难度,有利于后续对引信系统的优化。

3 结论

本文中基于模糊故障树理论,提出一种引信安全性评估方法,对引信模糊故障树的构建和分析进行阐述,并结合典型无线电引信故障树实例,对其的部分作用过程建立模糊故障树,进行安全性评估和重要度计算,还与传统的Bell静态故障树的可靠性计算和重要度分析进行了对比,通过对比得出结论:

1) 对某小口径高炮无线电引信在预定的解除保险和解除隔离流程开始前引信作用故障树为例进行故障分析时,模糊故障树计算所得的半故障率和失效率分别为8.4×10-6和2.1×10-9,Bell故障树计算所得的顶事件概率值约为1.2×10-9,与模糊故障树失效率为同一数量级且较接近,验证了使用模糊故障树方法进行引信安全性评估的可行性。

2) 在重要度计算分析中,对比模糊故障树和Bell故障树的计算结果发现:模糊故障树和Bell故障树的重要度计算结果基本都处于同一数量级下,证明了模糊故障树计算方法的可行性和准确性。但Bell故障树在故障树较为复杂或底事件较多时,重要度计算和分析比较困难。在引信系统工程应用中,可以同时采用模糊故障树和Bell故障树对引信进行安全性评估。

本文实例中半故障机理和规则的建立为假设估计,具体模型和数值需要收集专家意见和长期的工程统计,进行进一步研究。