网络排名变差算法在充电桩计量可信度评价中的应用

郭景涛，鲁 超，符惠群

1.天津市计量监督检测科学研究院 天津 300192；2.国家电能表质检中心（天津） 天津 300192；3.天津中电新能源研究院有限公司 天津 300384

0 引 言

由于社会活动的幂律特性，不同安装位置充电桩的计量重要性极不平均。有关研究已证实，充电桩的充电量、交易次数都呈长尾分布［1］。由于电动汽车能耗费用远低于燃油车，社会可以接受较大的电能计量误差，依照传统模式对充电桩逐台检定已不再具有经济上的合理性。

充电桩与电能表同属于电能计量器具，人们自然希望像电能表一样，将大数据方法应用于充电桩。然而不论是求解能量守恒方程［2］，还是使用其他数据处理方法［3］，都需要利用电网树形拓扑所蕴含的总表、分表约束关系，辅以远程数据采集技术。可是充电桩之间非但没有树形拓扑约束，就连完善一致的数据采集平台都还没有建立，如果生搬硬套电能表方案，则势必需要对已安装的充电桩实施改造，加装计量总表及数据采集模块。尽管一些充电站装有计量总表，但是能否获取其数据尚属未知，而且直流充电桩自身能量损耗与输出功率间的复杂函数关系也限制了这一方法应用［4］。因此，至少现阶段，将电能表的方案应用于充电桩还无法取得令人满意的成效。

那么充电桩之间是否存在某种约束关系呢？如果考虑到电动汽车这一中介因素，就会发现答案是肯定的。如果一台充电桩检定合格，成为计量可信度极高的充电桩，那么电动汽车就有可能将这种可信度传递给其他充电桩。此处车已经不再是一台机器，而是由驾驶员主导的人机复合智能体，可以凭借知识、经验、工具（如车载仪表）等为充电桩评分。这种评分可以是显性的投诉，也可以是隐性的“用脚投票”。评分既包含充电桩的计量因素，又包含便利性、停车费用等非计量因素，甚至不可避免地包含人的记忆、感觉等主观因素。上述所有决定评分的因素可统称为“消费体验”。

正如大众消费领域已经发生的，人们对充电的关注焦点也在变化：从单纯追求“足斤足两”延伸到追求消费体验；从寻求权威机构的背书扩展到参考大众评分。事实上，大量用户综合的评分本身就拥有权威性。对这一原理的经典应用要数谷歌PageRank网页排名算法［5］，该算法很好地展示了复杂信息网络的投票智慧，而充电桩与电动汽车的结合也构成了一个复杂信息网络。本文旨在挖掘其中的投票智慧，探索建立一种适用于充电桩的、相对于传统检定校准“弱”的计量评价方法，用于排除低风险的充电桩，使检定校准有的放矢。

本文研究的原则之一是立足于可获得的条件，极力避免向桩、车、环境提出更多要求。

1 桩车网络

根据一个时期内可获得的充电桩的交易流水数据，构造桩车网络。

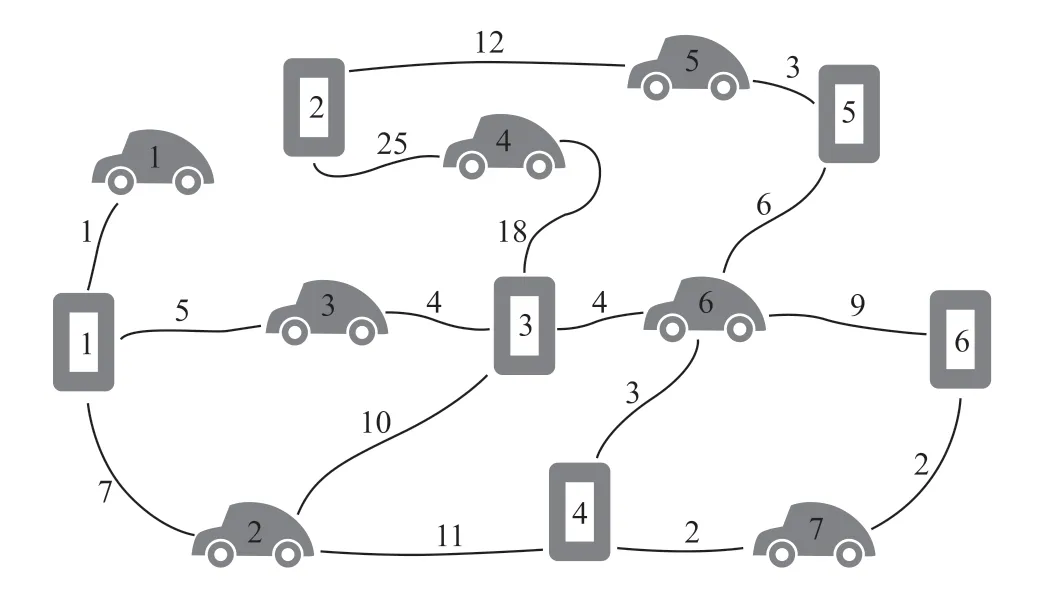
图1 由6 桩7 车构成的网络Fig.1 Network consisting of 6 piles and 7 vehicles

桩车网络可以用矩阵表示，以行区分桩、列区分车。如果用矩阵元素表示对应的桩车连接次数，则图1 网络可用式（1）表示。

如果将连接次数达到2 次的连接视为有效连接（理由见下文第3.2 节），并且仅考虑连通性，那么就能得到图2 网络，相应的矩阵为式（2）。

图2 仅考虑连通性的网络Fig.2 Network considering connectivity only

2 排名变差算法

2.1 原理

此处没有明确评分和排名的含义及其影响因素。事实上，明确这两点既困难又无必要。只要能够确定评分和排名都是由桩车网络连接状况决定的比较稳定的量，那么计量之外的诸多影响因素在两次排名中都存在，因而会在计算变差时相互抵消。

2.2 评分

再假设④，即权威度高的车鉴别力较强，所选择桩的评分也较高。因此，用桩的平均分作为车的评分，构造式（5）。

2.3 评分的计算

式（4）（5）给出了桩与车评分的依赖关系。如果以某种方式为评分赋予初值，那么可以通过式（6）迭代计算评分，其中k为迭代步数。

改写式（6）为矩阵形式，其中T表示矩阵的转置。

组成式（7）中L的各列向量中，除了与孤立车节点（如图2 中1 号车）对应的为0 外，其余均为概率向量，即各元素之和为1。对于图2 网络，L为式（8）。

将式（8）中第二式代入第一式，得到式（9）。

式（9）给出了计算LLT主特征向量的迭代幂法。因为LLT为半正定对称阵，可以对角化，又因为本文只关注主特征向量（而非特征值），所以幂法按式（10）迭代。

为使结果收敛于唯一值，必须使LLT不可约，因此，对其做素性调整，得到式（11）。

2.4 引入控制变量

检定合格可以提高桩的评分。评分的提高可视为某个概率向量v向特定桩倾斜的结果。而在此之前，这个概率向量是均匀分布的e /n。因此，以控制变量v代替式（11）中的e /n，得到式（12）。

3 算 例

3.1 桩的初始排名

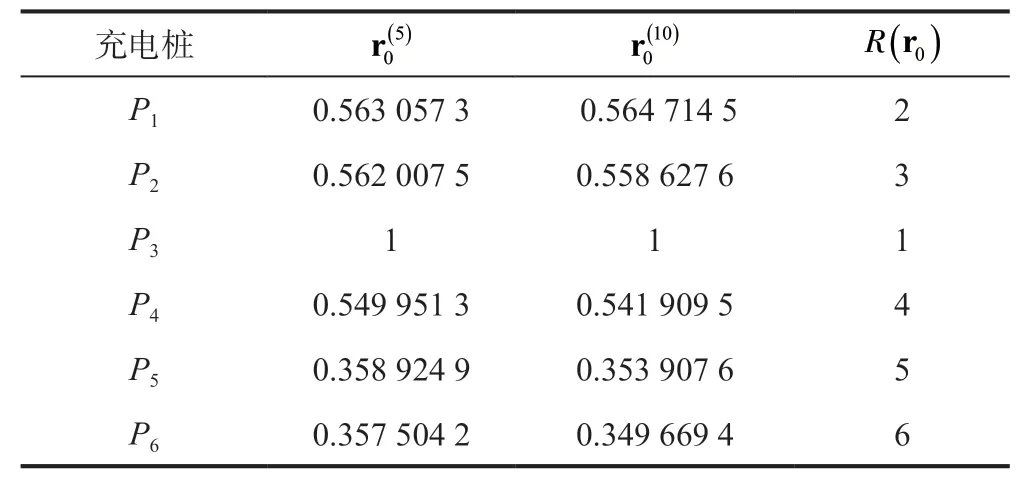
表1 初始充电桩排名Tab.1 Initial piles ranking

3.2 有控制变量的排名

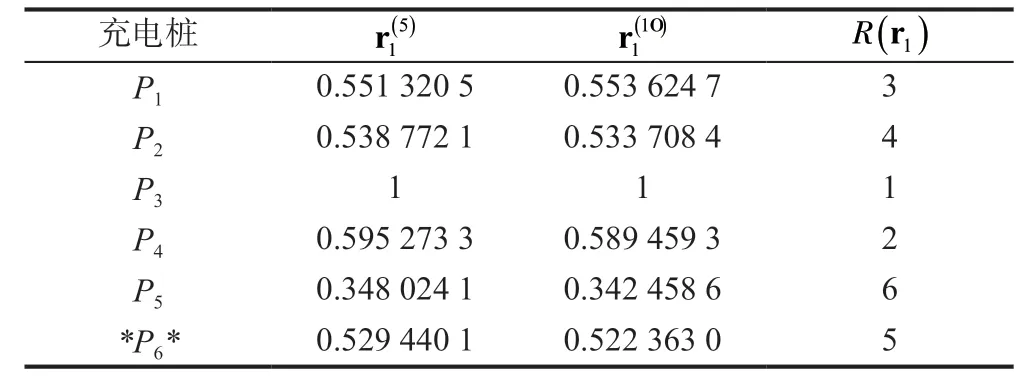
表2 v1 作用时的排名Tab.2 Ranking considering v1

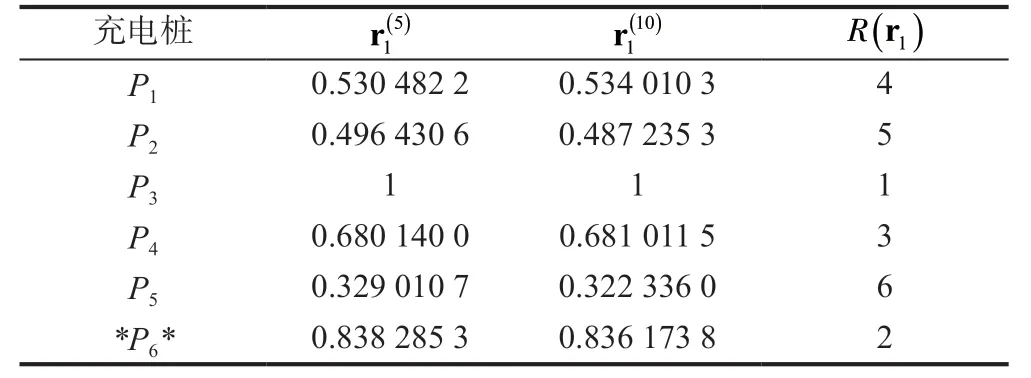
表3 v2 作用时的排名Tab.3 Ranking considering v2

3.3 排名变差

基于表1、2 数据，计算v1作用下的排名变差，结果见表4。基于表1、3 数据，计算v2作用下的排名变差，结果见表5。为负数时，表示排名上升，对应桩的计量可信度增加。

表4 v1 作用时的排名变差Tab.4 Ranking variation considering v1

表5 v2 作用时的排名变差Tab.5 Ranking variation considering v2

v倾斜程度不同时，排名变差会有不同，但是变化趋势一致。表4、5 都显示6 号桩和4号桩的排名上升，这是因为6 号车和7 号车将6 号桩的计量可信度传播到了4 号桩。

4 讨 论

对比表1～3 数据可知，因为网络效应，所以v引起了几乎所有桩的评分改变。本文以排名变差而非评分变差作为评价计量特性传播的依据，这是因为自然数排名具有离散性和排他性，所以相比实数评分而言更加显著和稳定。然而是否能够直接以评分变差作为评价依据，还值得进一步研究。

算例中的控制变量不是真实施加于网络的，而是虚拟的，类似于力学研究中的“虚位移”，其目的在于给出一种任意桩对其他桩影响的计算方法。

算法对网络完整性没有要求，原则上该方法可应用于桩集合的任何子集。特别是当真实（而非虚拟）的控制变量施加于网络时，同一桩集合的排名变差能够反映出实际计量可信度的变化。

另外，可想而知，控制变量不只可以用来标记计量因素。排名变差原理还可用于研究其他因素的网络传播，发现那些对传播发挥关键作用的节点，使得资源的投放更有效率。

5 结论与展望

数据驱动的内涵之一是数据决定方法，必须根据能够获取的数据寻找适宜的方法。本文提出的排名变差算法以充电桩交易流水数据为前提条件，在一定程度上能够识别充电桩计量可信度的传播范围。需要强调的是，由于交易记录包含个人隐私，保管人在提交交易流水数据之前必须将个人信息进行编码处理。

无论互联网还是桩车网络，节点的排名都主要由节点间连接强度决定。互联网由于建立连接的代价极低，其排名可以很好地反映网页的质量。在桩车网络中，决定连接强度的因素众多，因而排名本身并不足以反映计量特性，受控计量变量引起的排名变差则具有大得多的参考价值。

网络排名变差算法中，排名变差原理是实质性的，而评分算法是非实质性的，可以有多种选择，是否存在更适宜的评分算法有待进一步研究。■