基于WRF-LES模式的大气边界层近地风场精细化模拟研究

刘达琳, 陶 韬, 曹 勇, 周 岱, 韩兆龙

(1. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;2. 安徽工程大学 建筑工程学院,安徽 芜湖 241060)

近年来,全球性气候变化使得我国台风灾害频发,对沿海的房屋建筑造成巨大影响,如台风“莫拉克”造成的房屋倒塌有1.4万间[1].台风等极端气象对人类产生直接危害的风场来自更加靠近地面的大气边界层.研究大气边界层,预测边界层特性,对建筑结构抗风系数设计、土木工程防灾减灾具有重要意义[2-4].

精细研究大气边界层特性常用的风工程方法主要有现场实测、风洞实验和数值模拟等3类.与现场实测和风洞实验相比,数值模拟方法不受探测技术、设备性能、地理因素等客观因素限制,成为使用更多的研究手段.Fluent等经典软件未考虑地表能量平衡计算、云微物理参数化等气象模式,因此在真实大气应用中存在一定缺陷;此外,由于运算能力和时间的限制,Fluent等经典软件不适合较大范围的风场模拟,而数值天气预报(Weather Research and Forecasting,WRF)系统可以弥补这些缺陷.WRF模式具有参数多、方案新、精度高、易嵌套等特点和优点,可用于预测、重现大气边界层风场特性.文献[5]中利用WRF模式数值模拟兰州河谷盆地区域,获得的风场和温度场模拟结果与观测基本一致,为缓解城市热岛效应提供了参考依据.文献[6]中采用WRF模式对台风“鹦鹉”进行高时空分辨率模拟,通过分析台风模拟路径、气压分布、风速模式等风场特性,发现WRF模式能有效模拟近地面台风风场,为后续小尺度数值模拟提供真实的入流风场.Yuan等[7]采用WRF模式对真实陆上风电场内的流动特性和功率输出特性展开高分辨的数值模拟,利用风电场的观测数据进行验证,结果表明,WRF模式对于风场的风速、风向和风力机功率的模拟具有较高的精度.WRF模式汇聚了不同学者描述不同物理过程的参数化方案,它们各有特点和使用条件限制,因而会影响数值模拟的稳定性和精度,如空间差分格式方案和次网格模型方案对精细化模拟产生影响.Wicker等[8]对比通量的三阶、四阶、五阶和六阶形式,发现奇数阶算法是更高一阶(偶数阶)算法的线性组合,具有数值耗散性.Janjic等[9]在非线性试验中发现四阶差分格式比原始二阶差分格式对于小尺度能量积累更具有优势.Yamaguchi等[10]研究发现高阶对流方案有利于减少云模式的数值耗散.文献[11]中设计25个试验(水平对流项和垂直对流项分别采用二阶～六阶5种差分格式),开展非线性密度流试验研究,通过分析涡旋产生位置和发展,发现水平五阶差分和垂直三阶差分的组合方案,基本可消除不稳定扰动.大涡模拟(Large-Eddy Simulation, LES)方法通过直接求解大尺度涡,采用次网格模型参数化小尺度涡,有利于精细化模拟近地面风场,Deardoff[12]在1972年将大涡模拟应用于大气边界层的模拟.现有WRF版本集合了LES模块,通过修正WRF-LES模块的次网格模型而较好地呈现近地面风场特性.Moeng[13]在1984年LES中也采用了TKE闭合模式,但该方法所模拟的平均风速在近地面附近不满足相似理论的对数律.Moeng等[14]也在传统的Smagorinsky次网格模型添加修正项,以减小不同计算域间的表面摩擦偏差,改进后的模型较好地重现了热力驱动或风切变引起的边界层湍流特性,提高了大涡模拟的精度.Leith[15]考虑了湍能的逆向串级,提出随机后向散射次网格闭合模式.Mirocha等[16]在WRF-LES中添加非线性回波散射和各向异性(Nonlinear Backscatter and Anisotropy,NBA)模型,与线性模型相比,NBA模型明显降低近地面风速剖面与对数律预期之间的偏差,从瞬时风场图中发现其模拟的涡旋尺寸范围更广,能更好描述高分辨率下地面附近的流动分离.Kirkil等[17]利用WRF模式研究了拉格朗日平均尺度相关模型和动态重构模型,研究结果表明这两种动态次网格应力模型能够很好预测功率谱中惯性区域的产生和范围扩展,实现最好的动态模型的整体缩放,这种效果在地表附近效果更加明显.此外,网格分辨率也影响模拟的精度,Zheng等[18]发现提高网格分辨率对空气污染、降雨降水的预测非常重要.文献[19]中利用WRF-LES模式评估3种水平网格分辨率(120、60、30 m)和3种垂直网格分辨率(20、10、5 m)对对流层的影响,发现水平网格分辨率为30 m时,能在大气边界层范围获得理想的湍流再现,而垂直网格分辨率的提高对模拟结果影响较小.Mirocha等[16]发现网格纵横比(水平网格分辨率/垂直分辨率)为3～4时,平均风速剖面更加接近指数律.

上述研究运用WRF-LES模式模拟大气边界层,多采用均匀网格,尚缺少加密网格和非线性次网格模型、空间差分格式奇偶性对近地面风场精细化模拟影响的深入研究,可能会导致该模型难以准确模拟大气边界层近地风场特性.

本文基于WRF-LES模式,寻找适用于近地面风场精细化模拟的次网格模型方案、空间差分方案和网格设置方法.首先阐明数值模型的控制方程和湍流模型,然后阐述数值模拟方法,包括大气边界层的几何模型、边界条件和计算设置,随后讨论和分析了计算结果,最后进行总结.

1 数值模型

1.1 控制方程

利用WRF-LES模式开展理想大气边界层近地面风场特性的数值模拟,为了定量描述和预报边界层状况,文献[20]中引入可压缩流体的状态方程、连续性方程、动量方程、热力学方程和水分方程.考虑易读性,简化方程表示如下.

状态方程:

(1)

连续性方程:

(2)

动量方程:

(3)

热力学方程:

(4)

水分方程:

(5)

式中:ρ为空气密度;p为压强;T为温度;θ为位温;Rd为比气常数;xi、xj表示空间坐标,i,j=1, 2, 3;cp为比定压热容;ui为流体速度,i=1, 2, 3, 分别表示纬向分量、经向分量以及垂直分量;Sθ为热量的源汇项,分别由辐射、潜热、湍流及对流输送造成;Ωj为地转角速度在各方向上的分量;Fi为摩擦力项;qn为比湿;Sqn为水分的源汇项,n=1, 2, 3, 分别表示固态水、液态水和气态水;当i、j、k为相同数值或为偶排列时,εijk为0,当i、j、k为奇排列时,εijk为-1.

将动量方程在空间上进行过滤,只滤去小波脉动,保留大涡脉动,可得:

i,j,k=1, 2, 3

(6)

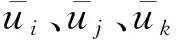
1.2湍流模型

为了封闭动量方程,WRF4.3提供4种次网格模型:标准Smagorinsky模型(SMAG模型)、标准1.5阶湍动能闭合模型(TKE模型)、NBA1模型和NBA2模型.前两种模型假设次网格应力与涡黏系数是线性关系,而涡黏系数分别由Smagorinsky常数cs和ce来确定;后两种模型分别是在前两种模型的基础上额外增加非线性项,以考虑湍流反向级串和各向异性的影响.NBA1模型和NBA2模型的亚格子应力项[16,21]如下式所示:

(7)

(8)

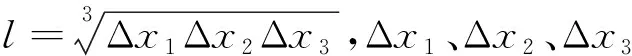
2 数值模拟方法

2.1 几何模型与计算网格

通过WRF-LES模式构建模型,以理想大气边界层为研究对象,研究次网格模型方案、网格分辨率方案和空间差分格式方案对大气边界层近地面风场特性的影响.表1给出理想大气边界层的模拟范围,水平和垂直的网格分辨率和网格数量,以及时间步长.对于次网格模型试验,水平网格分辨率取30 m,垂直网格分辨率取20 m,选用WRF4.3提供的4种次网格模型.对于网格分辨率试验,在一个基本算例(水平网格分辨率30 m,垂直网格分辨率 10 m)的基础上,选用只改变水平网格分辨率的4种试验方案和只改变垂直网格分辨率的5种试验方案.其中,不均匀加密方案的计算域如图1所示,入口风速为15 m/s,计算域长宽为 6 000 m,计算高度为 2 000 m.水平方向上网格分辨率取30 m,网格数为200×200,网格节点均匀分布.垂直方向上采用拉伸网格方案,如图2所示.图中:x1、x3分别为经度坐标和垂直坐标.在离地200 m范围内加密16层,第1层网格高度近似为3.54 m,网格膨胀率为1.1;200 m以上采用间距30 m的均匀网格.垂直网格不均匀加密方法可以在使用少量网格情况下,解决壁面黏性切应力的影响.对于空间差分格式试验,H代表水平对流,V代表垂直对流,例如H5V3表示为水平对流项取五阶差分,垂直对流项取三阶差分.

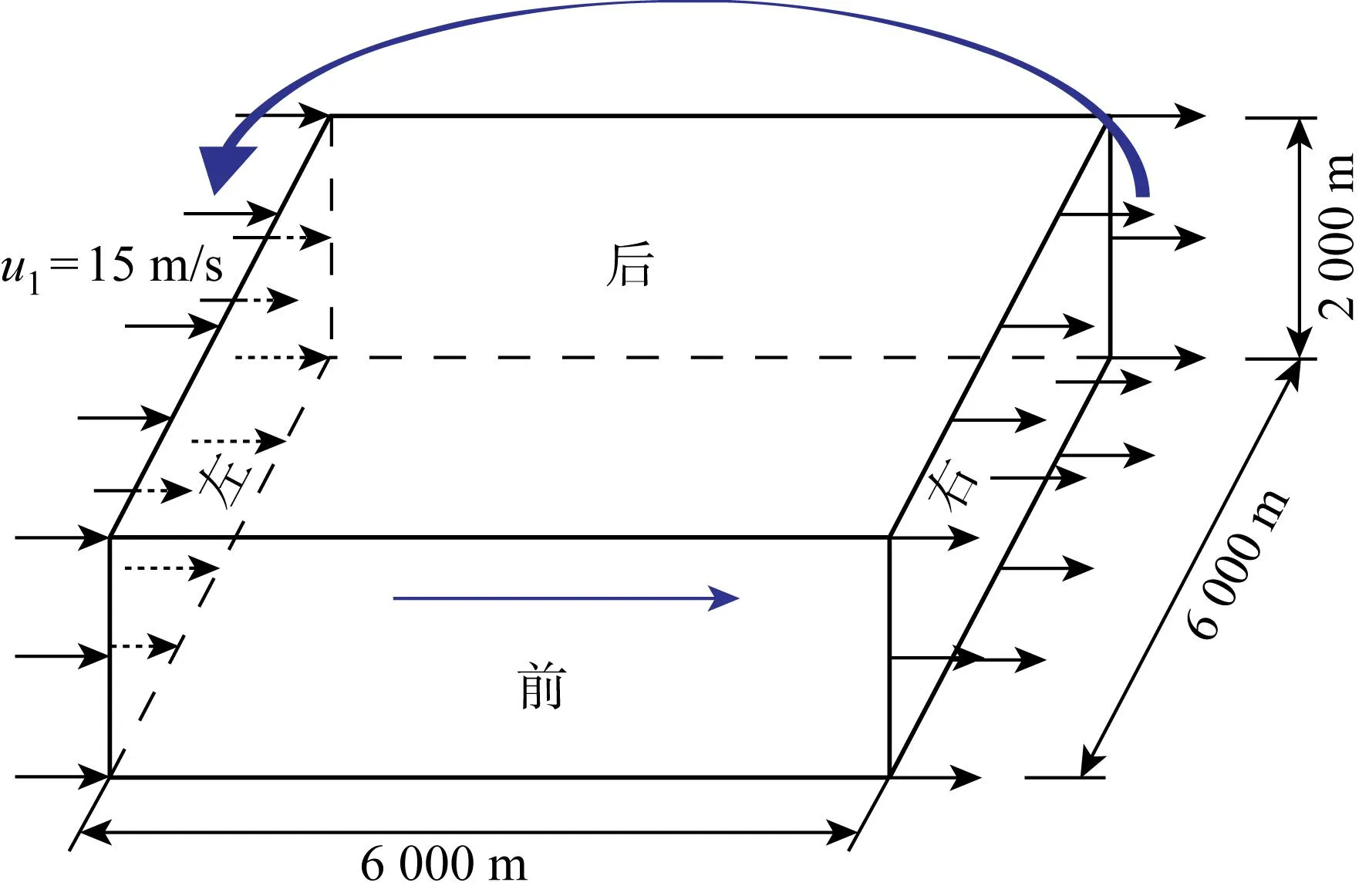
图1 理想大气边界层计算域 Fig.1 Computational domain for ideal atmosphere boundary layer

图2 垂直网格加密示意图Fig.2 Illustration of vertical grid mesh encryption

表1 基于WRF-LES的次网格模型方案、网格分辨率分案和空间差分格式的试验模拟参数Tab.1 Experimental simulation parameters of subfilter-scale stress models, mesh schemes, and spatial difference schemes based on WRF-LES

2.2 计算设置

计算域左侧为速度入口,右侧为速度出口,前后左右均为周期性边界条件,顶部边界条件光滑无渗透,表面层方案采用基于Monin-Obukhov相似理论[22]的改进MM5方案,该相似理论与风工程中常用的壁面函数一致,由以下公式确定:

(9)

(10)

式中:τsurf为地表摩擦力;u*为摩擦速度;ua为z高度处的风速;Cd为摩擦因数;z0为地面粗糙度;κ为von Karman常数,取值0.4;L为Obukhov长度;U为顺风向风速;ψ为大气稳定度的方程[23],在此不赘述.

地面粗糙长度设为0.1 m.时间积分方案采用三阶Runge-Kutta方法.所有其他物理选项均关闭,如微物理过程、积云方案、陆面过程、辐射过程等.计算时间为20 h(次网格模型中的NBA1和NBA2方案除外),每隔1 h存储一次模拟的全流域结果.设立55个监测点,记录每个时间步监测点剖面的风速,最后2 h的监测点数据用于结果统计分析.将最后2 h的统计数据与更长时间计算得到的数据进行对比,发现二者数据较为吻合,验证了时长的独立性.

3 WRF-LES计算方法验证

根据文献[16]中的计算设置验证WRF-LES计算方法的准确性.该试验中,大气边界层高度Ha=1 000 m,水平网格分辨率设为32 m,水平格点数为128,垂直网格分辨率设为8 m,垂直格点数为125,次网格模型采用Smagorinsky方案,时间积分方案采用三阶Runge-Kutta,水平对流项采用五阶差分,垂直对流项采用三阶差分.将计算稳定后的平均风速剖面与文献[16]中进行对比,如图3所示.

图3 试验模拟和参考文献[16]结果的平均风速剖面对Fig.3 Validation of the numerical model by comparing the wind speed profiles between test result and reference result[16]

由图3可知,本节试验与文献[16]中的平均风速剖面基本吻合,二者最大的相对误差为8%,出现在47 m高度处,其余误差基本小于5%.尽管试验模拟结果略大于已有文献,但这种误差是可以接受的.

4 计算结果和分析

4.1 次网格模型对大气边界层模拟结果的影响

图4给出不同次网格模型下的平均风速剖面.从图4(a)可以看出,水平风速在近地面呈现近似指数函数的上升规律,大约在120 m高度处逐渐变陡,直到 1 000 m 大气边界层高度处停止并再次出现转折.本文不讨论大气边界层宏观空间的问题,而是聚焦近地面的风场特征.近地面层是最接近下垫面的大气部分,高度通常在50～100 m[24],因此把近地面高度定为100 m.

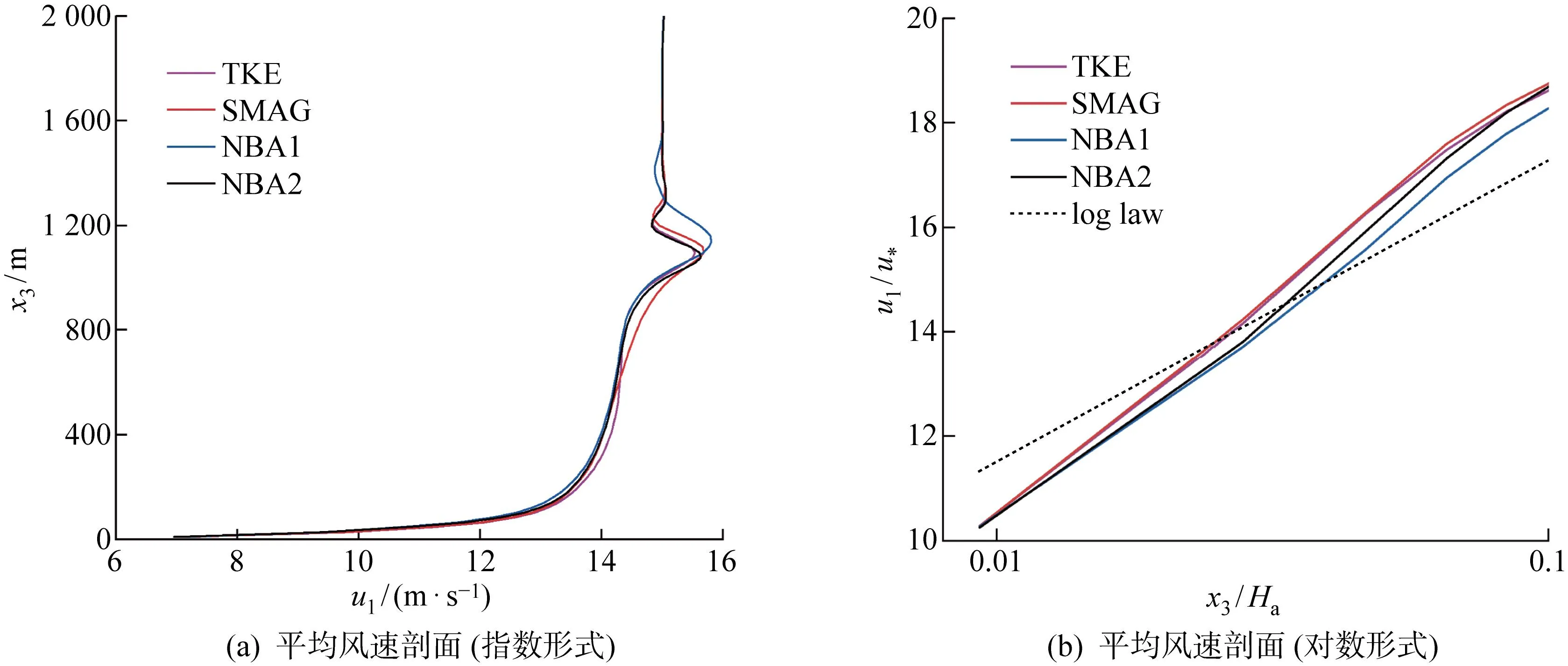
图4 不同的次网格模型方案下平均风速剖面Fig.4 Mean wind speed profiles of different subfilter-scale stress models

将图4(a)平均风速剖面在近地面处进行无量纲化处理,与对数律(log law)进行对比,如图4(b)所示.在对数坐标下,平均风速剖面与理论曲线吻合较好,初步验证WRF-LES方法可行性.此外,可看出模拟的水平风速在近地面处均大于理论值;较标准TKE模型或SMAG模型,NBA模拟结果更接近对数律理论值,模拟效果更好.

表2进一步定量分析次网格模型的模拟精度,结果表明NBA1模拟的平均风速与对数律的相对误差基本最小,与文献[16]中发现的结果一致.这是因为采用标准TKE模型或SMAG模型时,只能参数化正向的湍流能量串级而无法估算反向的能量输送,所以会高估近地层的风速切变[25-26].但在NBA模型中考虑次网格随机扰动作用[27],即考虑了能量可以从小尺度涡旋往大尺度涡旋传输;同时引入非均匀因子[28],使得风切变在近地层引起湍流各向异性,导致次网格的湍动能重新分配,从而一定程度上修正风切变对风剖面影响,提高近地风场的模拟精度.

表2 不同的次网格模型方案下平均风速模拟结果与对数律的相对误差Tab.2 Relative error between the simulated mean wind speed and log law of different subfilter-scale stress models

图5给出近地面范围内不同次网格模型的水平方向湍流强度I1,可看出湍流强度基本在0.12～0.22波动,而且30～100 m高度内NBA模型的湍流强度明显大于标准TKE模型或SMAG模型,在相同的高度处,不同次网格模型间的相对误差可达到10%,这可能是因为NBA中的非线性成分对来流扰动作用增强,使得湍流强度更大.

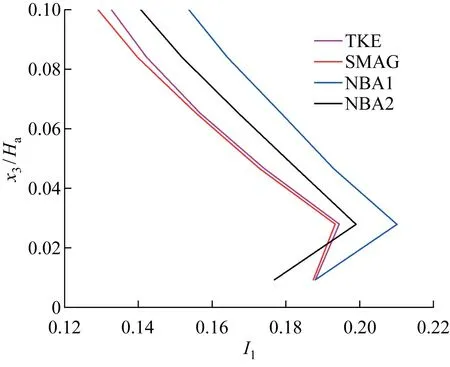
图5 不同的次网格模型方案下湍流强度剖面Fig.5 Turbulence intensity profiles of different subfilter-scale stress models

取所有监测点的顺风向风速序列,分别做功率谱,空间平均后再拟合处理,具体结果如图6所示.图中:f表示频率;S(f)为风速谱;σu为顺风向速度脉动均方根.从图中可以看出,频率处于0.025～0.03 Hz之间,功率谱在双对数坐标图中呈现出明显的线性特性,所有次网格模型都有相似的谱能下降速率,截止频率都近似在0.03 Hz,但频率大于0.03 Hz部分,TKE和SMAG线性次网格模型较非线性NBA次网格模型功率谱幅值下降更快.为了进一步定量分析数值解析湍流成分的最小尺度,下文重点关注有效网格分辨率.有效网格分辨率、截断波长附近的能量衰减模式动能谱显著偏离实际大气动能谱的波长.由文献[27]中分析大气行为的基本特征,发现在大尺度区域(500～5 000 km)动能谱(E)与波数(r)近似满足E∝r-3关系,过渡到中尺度区域(400 km以下)近似满足E∝r-5/3关系,结合泰勒冻结假设,建立功率谱与有效网格分辨率的计算模型如下:

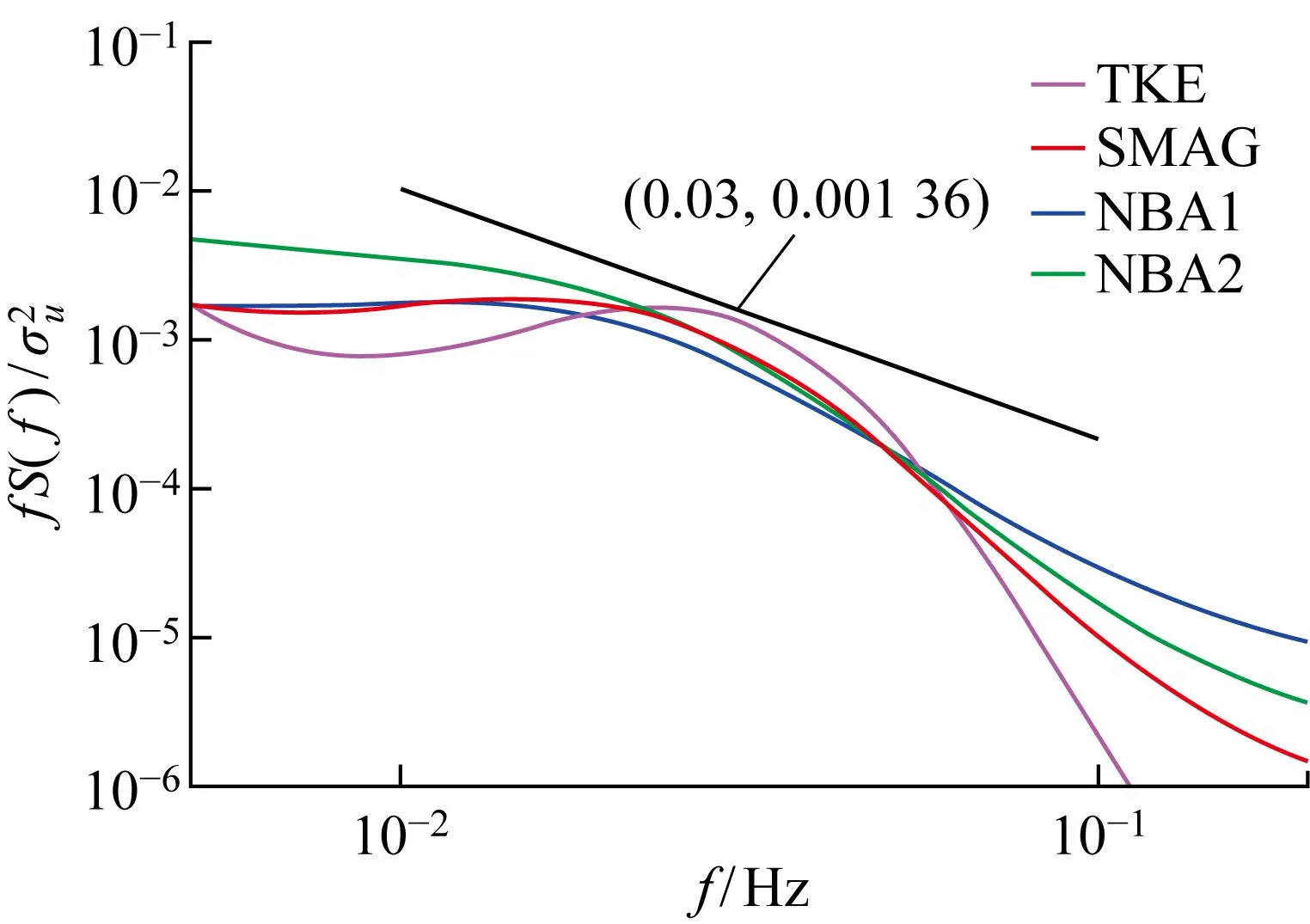
图6 在100 m高度处,不同的次网格模型方案的功率谱Fig.6 Power spectrum of different subfilter-scale stress models at 100 m above the surface

式中:λe为有效网格分辨率;fe为有效频率.

根据上式计算得有效网格分辨率近似为12Δx.但在其他文献中,文献[29]中采用动能谱评估WRF模式,确定7Δx为WRF模式的有效网格分辨率;文献[30]中也发现WRF-LES模式可以分辨7倍格距波长.但本文得到的有效网格分辨率较高,可能是因为本文通过功率谱与斜率为 -5/3 的直线严格相切来确定有效网格分辨率,而文献[27-28]中则依据斜率变化大致进行判断.另外参考文献[30-31],还对水平分辨率为8.2、30、90 和270 m的功率谱进行严格相切,发现有效网格分辨率近似在11～15倍格距,与本文结果基本一致.

因此,综合水平风速剖面、湍流强度剖面和有效网格分辨率等方面考虑,确定NBA1模型为次网格模型的最佳选择.

4.2 网格分辨率对大气边界层模拟结果的影响

网格分辨率对数值模拟的影响是一个相对复杂的问题.一方面数值模拟精度依赖于网格分辨率,为提高数值模拟精度要求网格分辨率尽可能高,尤其是在壁面附近;另一方面,受计算条件限制,网格分辨率不能无限增加.因此,讨论如何在节约计算资源下优化网格设计,使得模拟结果真实可靠.

图7 不同水平网格分辨率和垂直网格分辨方案的平均风速剖面Fig.7 Mean wind speed profiles of different mesh resolution cases

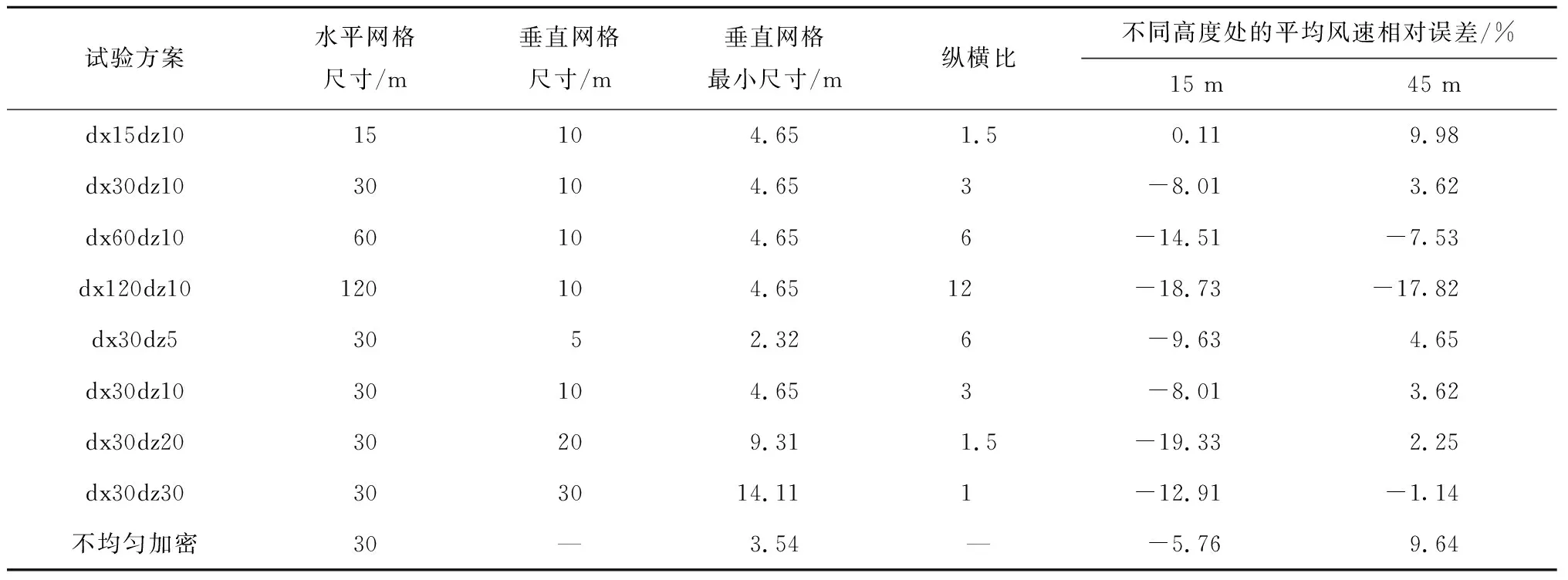
表3 不同水平网格分辨率和垂直网格分辨率方案下平均风速模拟结果与对数律的相对误差Tab.3 Relative error between the simulated mean wind speed and log law of different horizontal and vertical mesh cases

由图7(b)可看出,尽管垂直网格不均匀加密对平均风速剖面影响不大,但在近地面处会使其结果更靠近对数律,结合表3,当垂直网格最小尺寸越小,近地面平均风速的相对误差会一定程度上减小.此外,当垂直网格分辨率从 30 m 加密到 20 m (网格数为400万)时,模拟结果已经开始收敛,若采用垂直网格不均匀设计(网格数为308万),网格总量降低了23%,显著降低计算规模,在满足精度要求下提高计算效率,因此有必要加密近地面网格.并且当网格纵横比为3,相对误差能控制在10%以内,模拟效果较好.

图8给出不同网格分辨率下的湍流强度剖面,可以看到湍流强度基本在0.12～0.24波动,但在不同高度处湍流强度变化存在差异;当采用相同的垂直网格分辨率时,如图8(a)所示,湍流强度在一定高度范围内随水平网格分辨率增加而增加,湍流强度拐点高度近似都为15 m;当采用相同的水平网格分辨率时,如图8(b)所示,湍流强度在一定高度范围内也随垂直网格分辨率增加而增加.而超出某个高度,湍流强度会随水平网格分辨率或垂直网格分辨率增加而减小,这可能因为当网格分辨率越高,模拟的平均风速越接近入口风速,即平均风速越大,从而湍流强度减小.此外,如图8(b)所示,湍流强度拐点高度会随垂直网格分辨率变化而变化,当垂直网格分辨率为10 m时,湍流强度拐点高度近似为5 m,当垂直网格分辨率为30 m时,湍流强度拐点高度近似为 45 m;模拟结果的湍流度剖面拐点通常出现在地面以上第2层网格处.原因在于真实大气的湍流度越靠近地面越大,然而在模拟中,由于靠近地面网格分辨率和壁面边界条件的限制,第1层的湍流难以充分直接解析,所以最高湍流度往往出现在第2层.

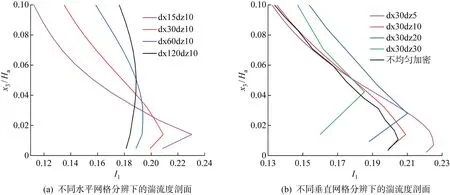
图8 不同网格分辨率方案下的湍流强度剖面Fig.8 Turbulence intensity profiles of different mesh resolution cases

综上考虑,推荐水平网格分辨率为30 m,垂直网格分辨率为10 m,垂直网格在近地面区域适度加密.

4.3 空间差分格式对大气边界层模拟结果的影响

空间差分格式会影响N-S方程对流项的求解,为了解空间差分格式对理想大气边界层数值模拟影响,图9给出不同空间差分格式的平均风速剖面.可知,所有空间差分格式的无量纲化平均风速基本都在14.5～18.0波动,与对数律非常接近,所有相对误差基本控制在5%以内,说明空间差分格式对平均风速剖面影响不大.

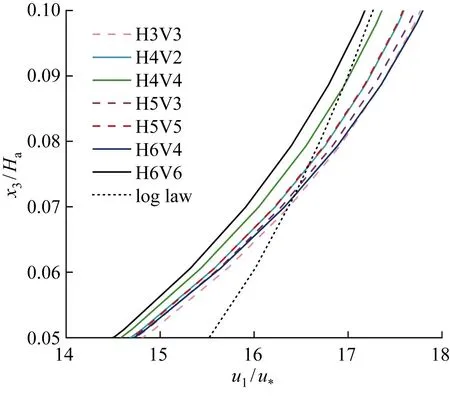
图9 不同空间差分格式方案下的平均风速剖面Fig.9 Mean wind speed profiles of different advection differential cases

图10给出不同空间差分格式在近地面范围的湍流强度剖面.由图可知,空间差分格式在约40 m 高度范围内存在明显的差异,奇数阶差分格式较偶数阶的湍流强度更大;但在 40 m 高度以上,所有空间差分格式的湍流强度都趋于0.16.

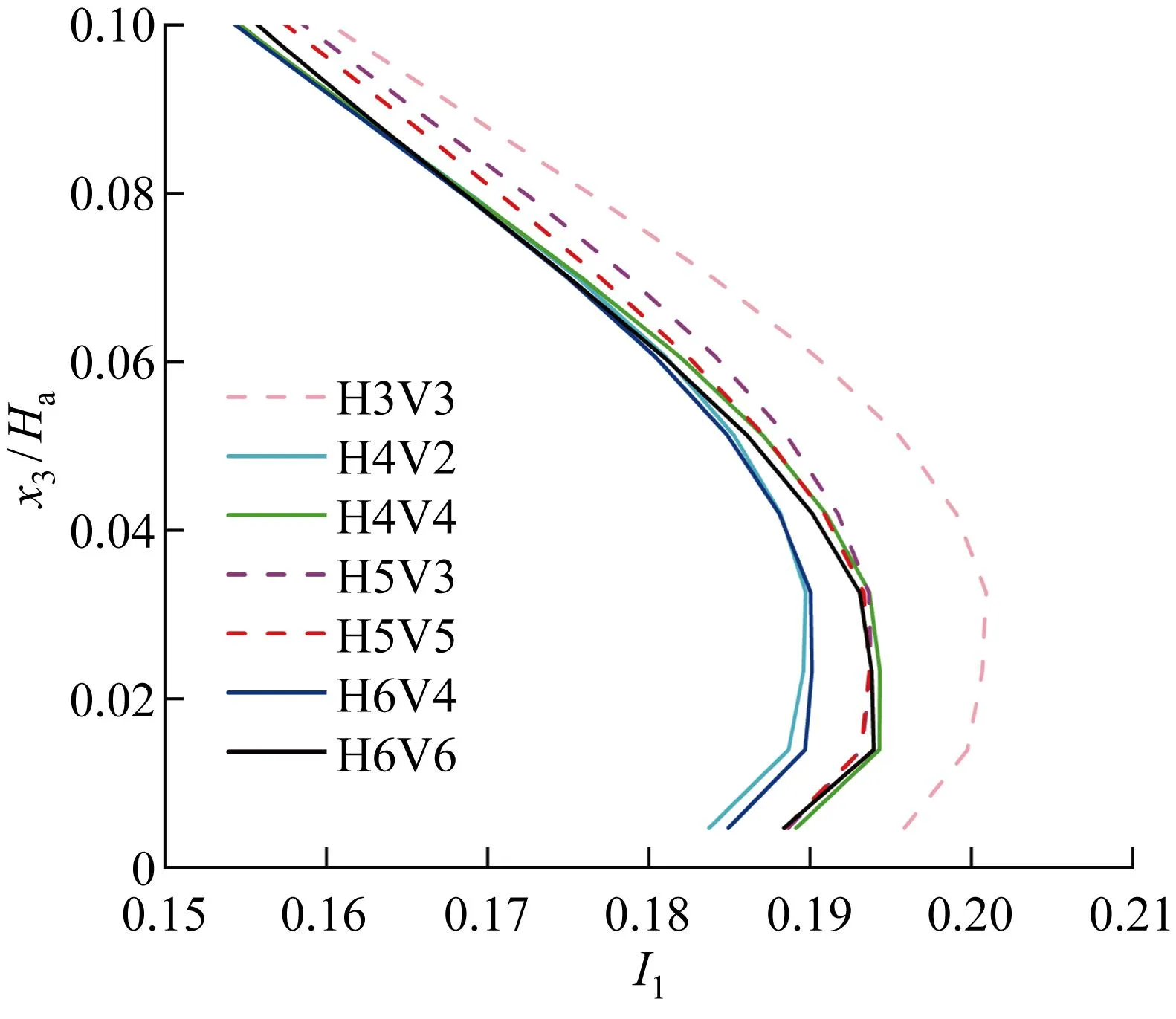
图10 不同空间差分格式方案下的湍流强度剖面Fig.10 Turbulence intensity profiles of different advection differential cases

图11给出不同空间差分格式在同一时刻的水平速度,剖面高度为z=40 m.由图可见,所有试验方案的流场图均有条带状结构,湍流结构有明显的组织性,而且受地转风影响,条带状结构呈现近似45° 方向.另外,由图可看到,偶数阶差分格式较奇数阶明显能捕获更小尺度的湍流结构,出现这种差异的原因可能是奇数阶差分格式较偶数阶增加了数值黏性,使得小尺度涡耗散,小尺度湍流结构消失.结合图12和表4,可得偶数阶差分格式的有效分辨率为(6～8)Δx,奇数阶的有效分辨率为(9～13)Δx,证实偶数阶差分格式能获得更小尺度的湍流结构.

图11 在40 m高度处,不同空间差分格式方案下x-y平面水平速度的瞬时风场Fig.11 Contours of instantaneous velocity in the x-y plane at 40 m above the surface from different advection differential cases

图12 在40 m高度处,不同空间差分格式方案下的功率谱Fig.12 Power spectrum of different advection differential cases at 40 m

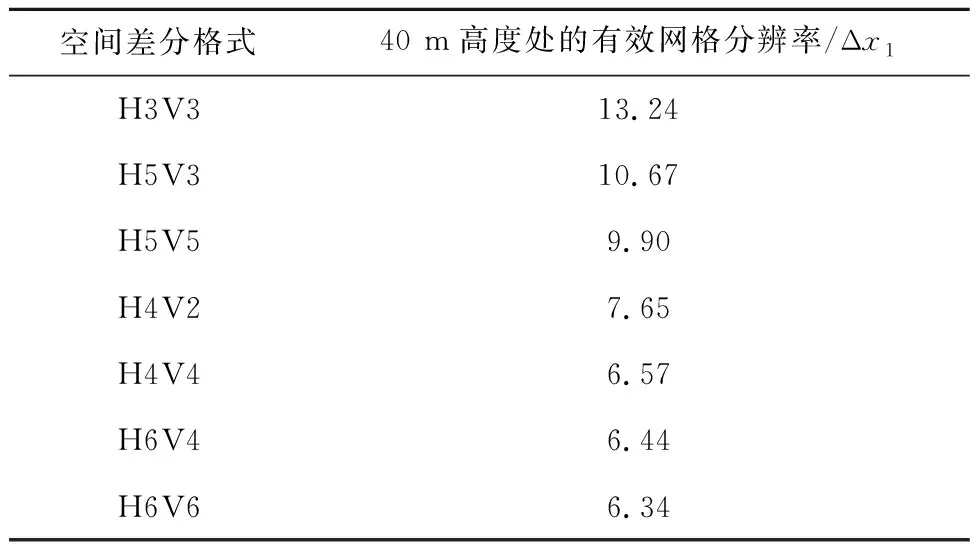
表4 不同空间差分格式方案下,40 m高度处的有效网格分辨率Tab.4 Effective resolutions of the different advection differential cases at 40 m

5 结论

利用WRF-LES模式对理想大气边界层进行模拟,结合平均风速剖面、湍流强度和功率谱等数据,分析次网格模型、网格分辨率和空间差分格式对近地面风场模拟的影响.主要结论如下:

(1) 与标准TKE模型或SMAG模型相比,NBA1次网格模型考虑了湍动能的反向级串,可更充分揭示湍流性态,更准确地模拟理想大气边界层近地面的风场特性.

(2) 结合水平网格分辨率(15、30、60和120 m)和垂直网格分辨率(5、10、20、30 m和不均匀加密)试验方案,评估其在近地面的模拟精度,建议网格纵横比设为3,水平网格分辨率采用30 m,垂直网格分辨率采用10 m;垂直网格在近地面区域适当加密可有效节约计算资源.

(3) 空间差分格式对平均风速剖面影响不大,但在WRF-LES模式下,与奇数阶差分格式相比,偶数阶差分格式,可明显改善小尺度湍流结构的再现能力,即偶数阶差分格式有效分辨率达(6～8)Δx,而奇数阶差分格式的有效分辨率为(9～13)Δx.

合适的WRF-LES参数方案可显著提高近地面风场模拟精度,有望应用于台风边界层的精细化数值模拟,提高台风风速预测精度,为防台风减灾设计提供技术参考.