“图形变换” 凸显 “核心素养”——2023年温州市中考数学填空压轴题评析

朱 光 (邮编:325000)

浙江省温州市第十二中学

1 试题呈现

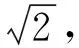
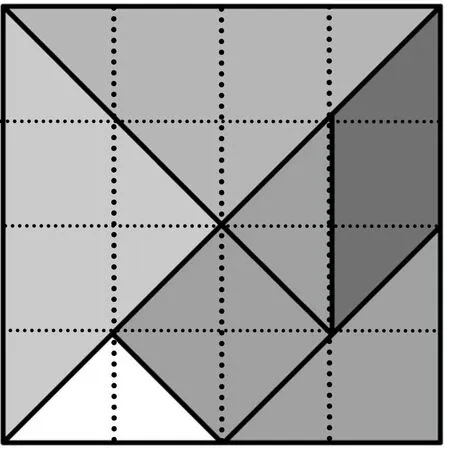
图1

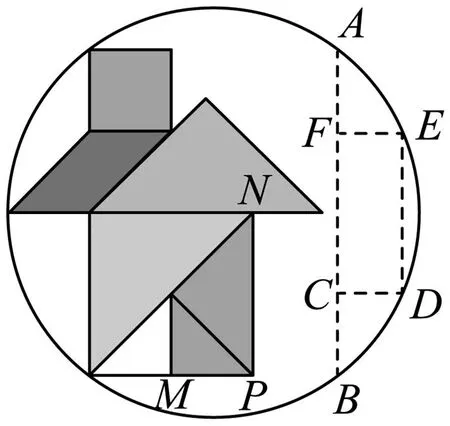
图2

2 试题评价

2.1 问题设计新颖,聚焦核心知识

本题用七巧板图案巧妙构筑了一个数学问题,它融合等腰直角三角形、平行四边形、正方形、相似三角形、圆等基本图形,图形变换自然．第(1)问起点较低,运用了垂径定理、勾股定理和方程思想等核心知识和方法．同时第(1)问为第(2)问做铺垫,两问联系紧密,梯度自然、合理．

2.2 猜想和推理的有效结合

七巧板由一些特殊几何图形构成,圆和拼成的“房子”具有很多的对称关系,易于学生在直观中发现等量关系．由图形易产生猜想:圆心是否在中间横线上?点A和点B是否在“房子”的上下水平延长线上?点N是否为圆心?猜想是解题的基础,没有猜想的引领,推理往往会迷失方向,同时猜想必须要经过推理论证．本题充分体现猜想验证思想．

2.3 在解决问题中凸显核心素养

《义务教育数学课程标准(2022年版)》指出,进一步加强综合与实践,以解决实际问题为重点．本题在解决问题的过程中,凸显了对数学抽象、几何直观、数学运算、推理能力、数学建模等核心素养的考查,展现了丰富的文化内涵和数学应用价值．

3 解法展示

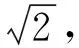
3.1 求圆的半径

分析 要求圆的半径,先要确定圆心．圆心必在弦的中垂线上．

思路1勾股定理+方程思想

解法1如图3,连结GH,易证GH=2=GQ,因为过左侧的三个点Q,K,L确定一个圆．QH=HL=4,又NK⊥QL,所以圆心O在KN上,连接OQ,设设OQ=r．则OH=r-KH=r-2,在Rt△OHQ中,因为OH2+QH2=QO2,所以(r-2)2+42=r2,解得:r=5．

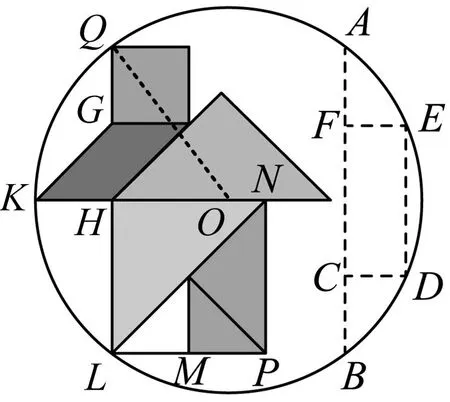
图3

思路2相似+方程思想

图4

3.2 求面积

分析在求得半径的基础上,对“点A,N,M在同一直线上”这一关键条件进行深度分析．如图5,可知∠ANS=∠AMP,通过先猜后验AN=MN,求得OS是关键．

图5

思路1利用相似(或三角函数)+勾股定理

思路2利用图形的对称性

图6

图7

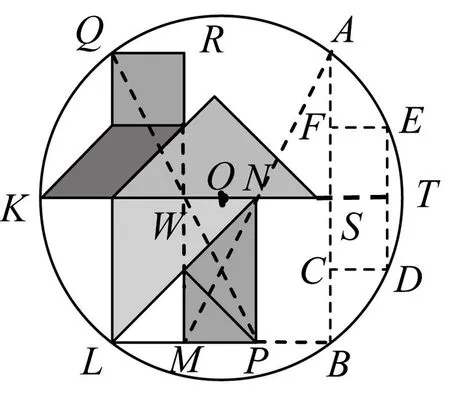
图8

解法4由解法3知MB⊥AB,易知点L,M,B三点共线,如图9,连结QA,因为QL∥AB,所以∠QLB=∠B=90°,因为A,Q,L,B由四点共圆,所以∠LQA=90°,且所以四边形AQLB为矩形,所以AB=QL．又因为OS⊥AB,KS⊥QL,所以OS=OH=3,后面同解法1．

图9

4 小结

本题解答思路丰富,还有很多解法不一一呈现．值得注意的是,有不少学生在求解第二空的过程中默认了L,P,B三点共线,或者默认点A在“房子”的上边所在的直线上．这是不严谨的,这样明显降低了求解的难度,存在运气成分．事实上,L,P,B三点共线与条件点A,N,M在同一直线上和已知线段的长度是密切相关的．