基于案例推理的刀具切削参数推荐方法研究
田 青,郭 宏,曹 铎,任必聪,任党阳
(太原科技大学 机械工程学院,太原 030024)
在生产制造中,刀具选用直接影响着切削的质量、效率、成本和能耗[1-2]。国内外对刀具及切削参数推荐方法进行了一定研究。文献[3]采用集合论对零件加工特征和刀具属性进行了定义和形式化描述,运用关系代数中的自然解运算构建了基于零件加工特征的刀具初选模型,并采用层次分析法对刀具初选模型进行优化解算。文献[4]以加工时间时间加工质量加工成本为决策指标,采用层次分析法与TOPSIS决策相结合来求解该模型,从而实现刀具选择。
案例推理(Case-Based-Reasoning)其原理是用通过检索与新问题相似的历史案例来解决现有问题的一种方法,其具有应用广泛、推理能力强、学习能力突出等优势,在多个领域得到应用[5]。文献[6]将案例推理应用于刀具选配中,并采用模糊理论的隶属度函数实现案例属性的相似度计算。文献[7]使用基于规则和案例区分材料的不同失效类型。
本文基于案例推理及语义计算、智能决策技术提出一种刀具及切削参数推荐方法,从众多可供选择的加工方案中选出符合用户需求的切削参数。
1 案例表示
案例表示是实现案例检索的基础,案例的表示即决定通过哪些属性信息来实现案例的匹配检索以及需要提供案例解决方案的哪些信息。案例表示通常包括问题描述及解决方法两部分内容。问题描述主要考虑切削加工的影响因素,在切削加工中,主要是对工件及加工要求的描述。解决方案提供在问题描述下使用的加工设备及工艺参数。
切削案例的问题描述如图1所示,主要从工艺类别、工件材料、工件形状以及加工要求四个方面进行。其中,工件材料通过材料类别、材料牌号以及硬度进行描述;工件形状通过工件类型以及加工面类型进行描述;加工要求由工件尺寸、加工精度两个属性进行确定。解决方案包含所选用的刀具、机床、切削参数以及切削液等信息。
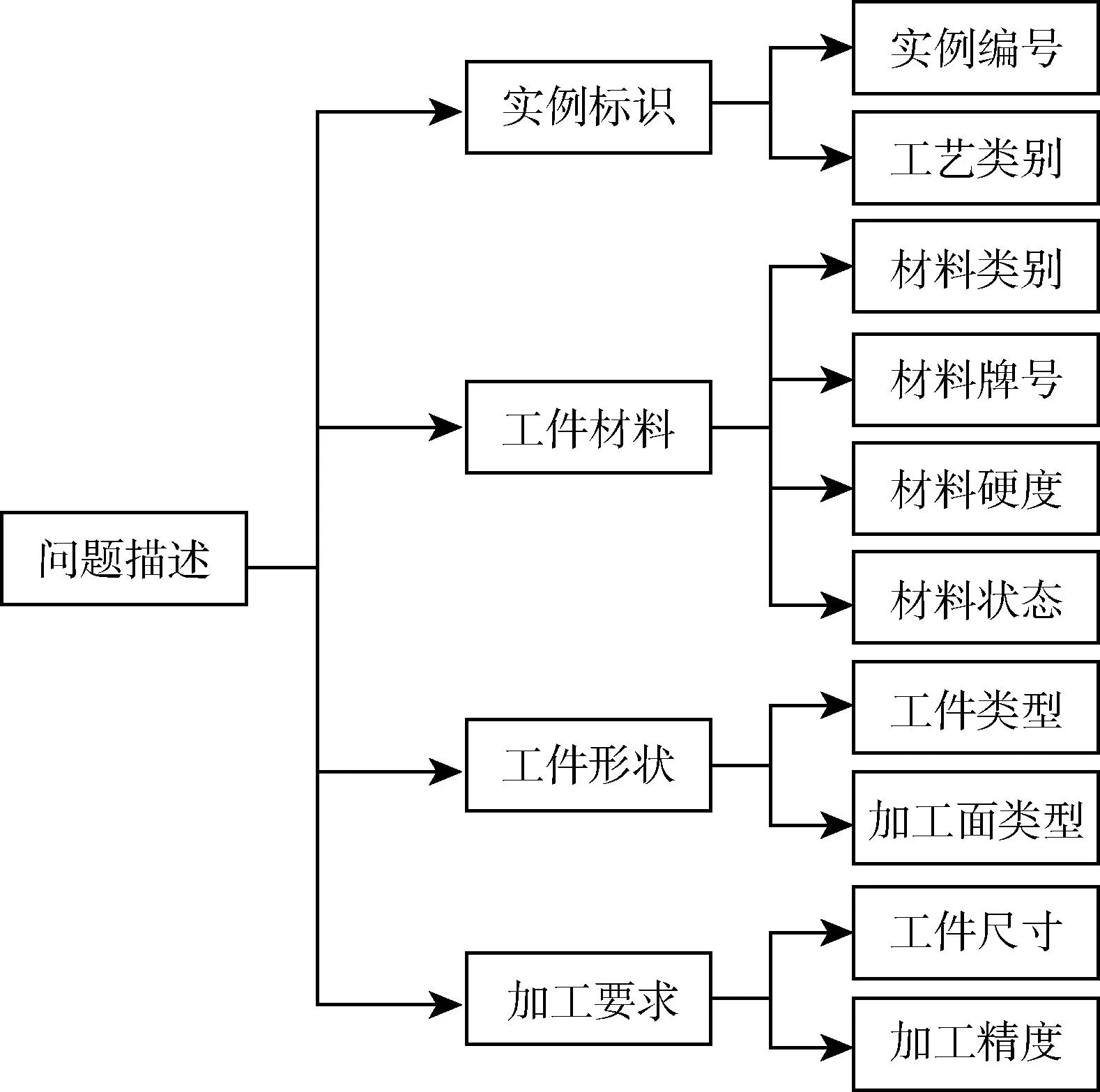
图1 加工案例问题描述
2 案例检索方法
传统的属性相似度基于属性距离值实现,但基于距离的方式忽视了属性之间的关联性。灰色关联分析法对数据量要求较少,与依赖比较序列的距离有所不同,其反映的是两个序列变化趋势的相近程度[8],本文将目标案例作为参考序列X0,案例库案例作为比较案例Xi,基于灰色关联法并结合主客观组合权重赋权对属性特征关联程度进行排序,从而完成案例筛选。
2.1 属性量化方法
特征属性可以分为离散型属性属性、连续型数值属性以及非数值属性,需要将非数值属性转为数值型属性以进行灰色关联分析。非数值属性可以分为语义型非数值属性、枚举型非数值属性与无关型数值属性。语义型非数值属性其中包含语义信息,通过构建切削本体,根据文献[9]与文献[10]结合使用的语义相似度算法对其进行语义计算,从而转换成为连续数值属性;枚举型非数值属性其中包含的语义信息较弱或者较难进行计算,通过将枚举值进行量化从而转为离散型数值属型;无关型属性可以通过式(1)进行转换。
(1)
本文所使用语义相似度计算方法如下:
AreaDensity(c1,c2)=
∑s∈AreaSubsumers(c1,c2)Density(s)
(2)
Density(s)=|Sons(s)|
(3)
AreaDepth(c1,c2)=
(4)
PathLendensity=
(5)
(6)
式中:x0(k)代表参考序列的第k个无关型属性,xi(k)代表第i个比较序列的第k个无关型属性。AreaDensity(c1,c2)为概念(c1,c2)的区域密度,AreaSubsumers(c1,c2)为去除c1,c2的最短路径经过节点,Density(s)为节点的密度,通过式(4)-(2)得到,其值等于子节点数目。AreaDepth(c1,c2)为区域节点深度,Depth(s)为节点深度,LCS(c1,c2)为最短路径中,c1及c2的祖先节点。λ为权重参数,取值为0.2.式(5)为相似度度量公式,α、β为调节权重,取值为0.5及0.55;d为LCS(c1,c2)的深度。
2.2 建立相似度决策矩阵
为了减小案例的搜索空间,首先通过工艺类别及工件类型对案例进行初步筛选,将筛选后的案例按照2.1节进行量化,得到由参考序列及比较序列组成的相似度决策矩阵。
X0={x0(1),x0(2),…,x0(k)}
(7)
Xi={xi(1),xi(2),…,xi(k)}
(8)
式中:X0代表参考序列,Xi代表第i个比较序列,xi(k)为第i个比较序列的第k个属性的值。
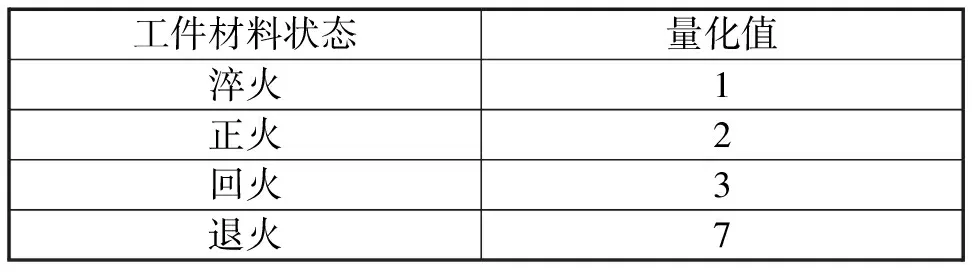
表1 材料状态转化表
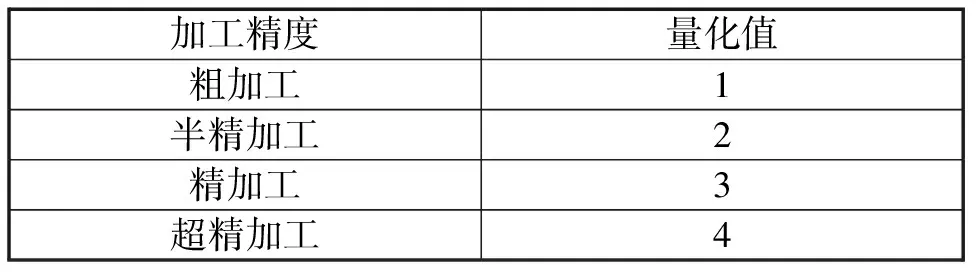
表2 加工精度转化表
2.3 灰色关联分析计算流程
在建立相似度决策矩阵后,需要从参考序列中,选取和参考序列相似度大的序列,案例间相似度的计算共分为四个步骤:
步骤一:归一化处理。
由于特征属性之间数据类型差异、取值范围差异较大,为消除量纲的影响,按公式(9)进行归一化处理。
(9)
式中:xi(k)与vi(k)分别表示第i个案例中第k个属性的属性值,以及归一化后第k个属性的属性值。
步骤二:计算灰色关联系数。
对经过归一化后得到的参考序列与比较序列,根据式(9)计算其灰色关联系数。
di(k)=
(10)
式中:r为区别系数,在(0,1)之间选取,通常将r取值为0.5.v0(k)与vi(k)分别为参考序列及比较序列中中第k个属性的值。
步骤三:计算灰色关联度。
由式(11)可得参考序列X0与比较序列Xi灰色关联度,其值由权重值与灰色关联系数乘积得到:
(11)
步骤四:灰色关联度进行排序。
灰色关联度反映了不同序列之间的相似相似度。根据公式(11),将计算得到的关联度由大到小进行排序,关联度越大则代表越与目标案例相似,从而为刀具及切削参数的选取提供决策依据。
2.4 属性权值的分配
案例描述中,不同属性的影响程度不同。本文将材料硬度、材料尺寸、材料类别、加工面类别等六个属性根据其对刀具及切削参数选用的影响程度不同分为三个等级,为不同等级的属性分配权值并进行归一化,所得权重值如表3所示。

表3 属性赋权表
3 切削参数推荐
根据灰色关联度可以匹配到与目标案例相似的案例,从而为刀具及切削参数的选用提供决策依据。但切削参数经常为多组数据或范围值,为了更好满足用户不同需求,需要对切削参数进行进一步推荐。在参考检索所得的切削参数后,通过正交实验采集所需数据,通过VIKOR理想点法完成切削参数的多目标决策。
3.1 VIKOE法的基本概念
VIKOR法是Opricovic S[11]提出的一种多指标决策方法,该方法的基本思想是首先计算各个方案的评价值与最理想解的接近程度,最后综合考虑群体效应及个体遗憾来获得排序,相比TOPSIS法更为接近理想方案[12]。因此,在本文中使用VIKOR妥协排序法对服务案例进行进一步筛选。
3.2 VIKOR分析流程
由于进行切削参数决策时的考虑不同,可能会出现相似案例提供多组切削参数的情况。本文使用VIKOR法对切削参数进行进一步优选:
步骤一:建立多属性决策矩阵。
从众多可行方案中对最佳方案进行选择是一个多属性决策问题,其可以由如下的矩阵表示:
(12)
(13)
式中:C1,C2,…,Cm为案例库中的历史案例,A1,A2,…,An为案例的不同属性,xij为第i个案例的第j个属性的属性值,wj为第j个属性的权重值。
步骤二:建立决策矩阵。
每一个rij按如下进行归一化计算
如果为效益性属性如切削速度则按公式(14)计算,
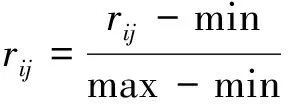
(14)
如果为成本性属性如背吃刀量和进给速度则按公式(15)进行计算。
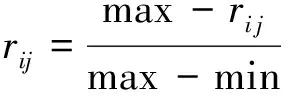
(15)
按照公式(16)得到决策矩阵Cv.
(16)
步骤三:属性权重确定。
由于多属性决策中属性的重要程度不同,需要对其进行权值的设置。极差分析常用于正交实验中,可以简单、直观的对实验因素的主次进行排列。属性权值的获取如下:
(17)
(18)
(19)
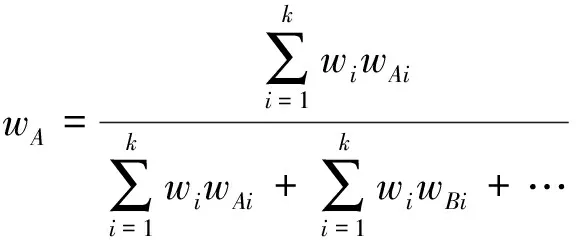
(20)
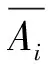
步骤四:计算群体效益值及个体遗憾值。
(21)
(22)
式中:ωj为第j项属性权重,Si为群体效益值,Ri为个体遗憾值。
步骤五:综合考虑最大群体效益与最小个体遗憾得到综合指标Qi,并将案例按数值从小到大进行排序,记为Cv1,Cv2,Cv3,…,Cvm.
(23)
其中,γ为群体效益权值,由用户根据需求进行选取。当γ>0.5时,代表用户偏向于群体最优γ<0.5,代表用户偏向于个体遗憾最小,通常可设置γ=0.5,以获得妥协解。
步骤六:根据判断准则确定最优服务资源案例。
最优方案需要通过两个条件进行判定:
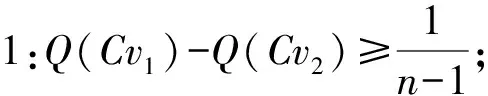
条件2:R(Cv1)=maxRi∧S(Cv1)=maxSi;
其中R(Cv1)为综合指标最小的Ri值,S(Cv1)为综合指标最小的Si值。若同时满足条件1与条件2,则Cv1为最优服务案例;若只满足条件1则Cv1、Cv2为妥协最优案例,若条件1不满足,则妥协最优案例为满足条件Q(Cvi)-Q(Cv1)<1/(n-1)的前i个服务案例。
4 实验验证
4.1 案例检索实例验证
为了说明所提方法的有效性和可行性,本文基于Protégé建立了如图2所示的分类本体,以平面铣削加工某箱体类工件为例进行说明。现已知零件的材料为经过退火处理的硬度150 HB的球墨铸铁,加工精度为半精加工,零件尺寸要求为1.0(长宽比),现要从案例库中筛选出相似案例以供工艺人员进行决策。经过工件类型及工艺类别初步筛选后,案例库中的案例如表4所示,通过本文所提方法对案例库案例进行检索。
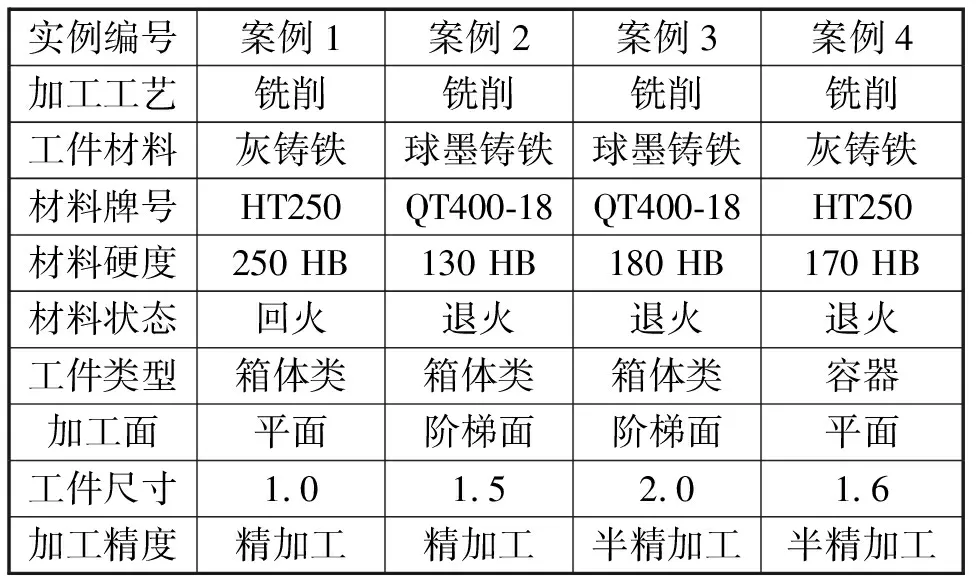
表4 铣削案例
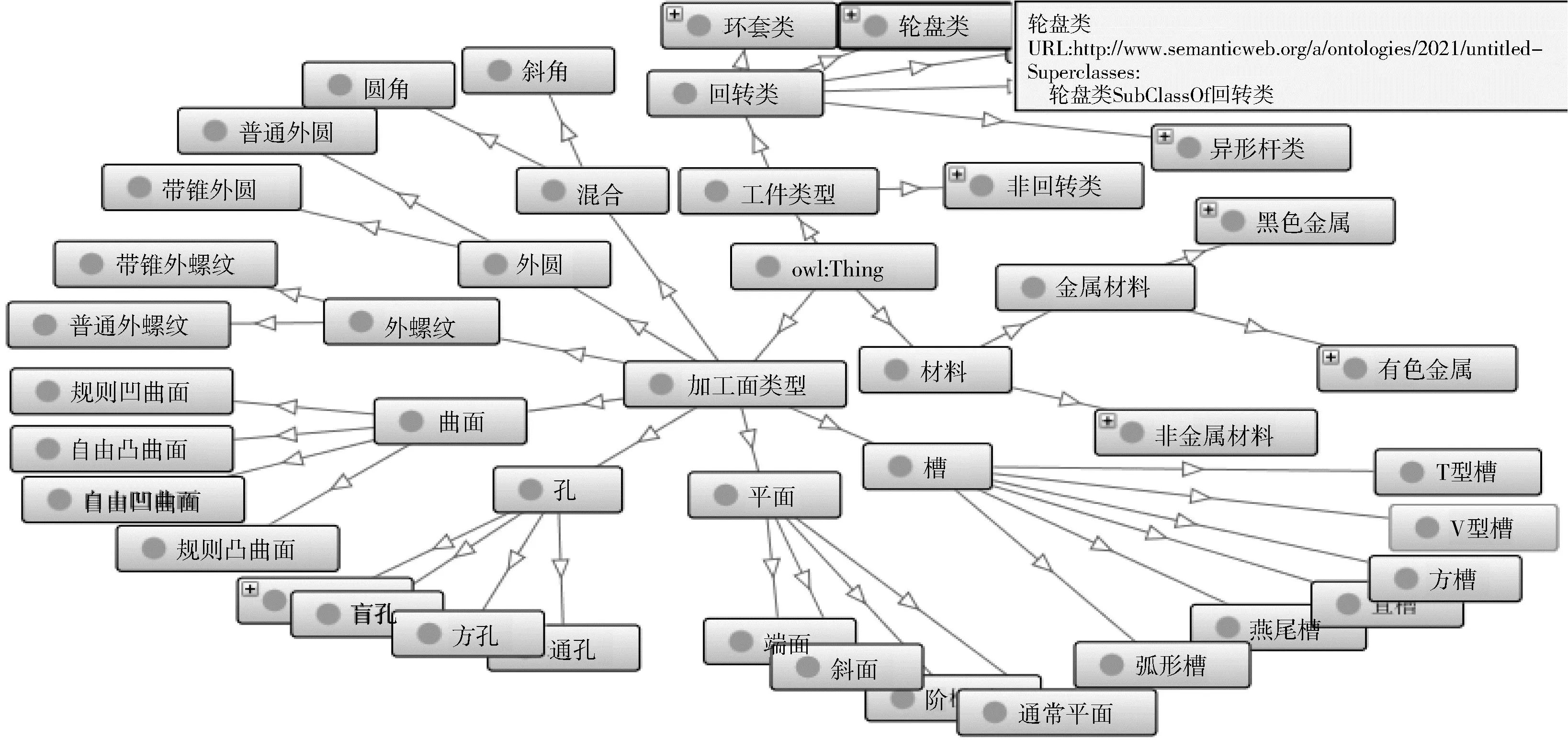
图2 本体结构图
将零件加工任务进行属性量化,生成参考序列,案例库中案例生成比较序列,根据公式(9)对各属性数据进行归一化处理后,采用公式(10)及公式(11)对案例计算灰色关联系数,所得结果如表5及表6所示。
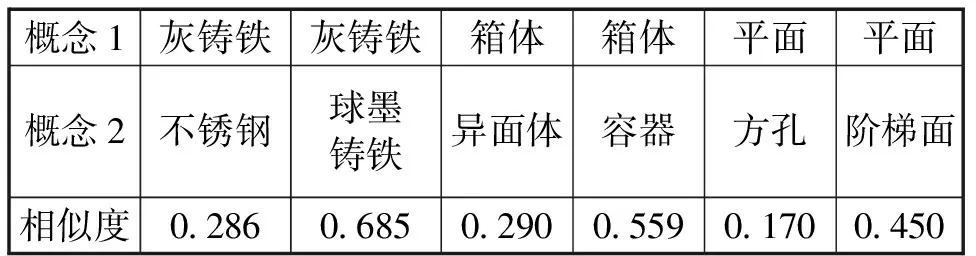
表5 语义计算结果
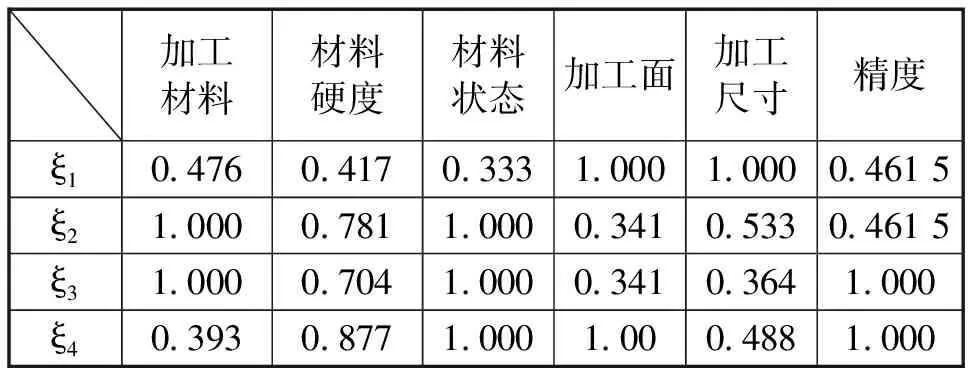
表6 关联系数计算结果
按公式(10)计算案例1至案例4与待求解问题之间的灰色关联度,并按照降序进行排序,其结果如下:
sim(x0,x1)=γ(x0,x1)=0.705
sim(x0,x2)=γ(x0,x2)=0.672
sim(x0,x3)=γ(x0,x3)=0.664
sim(x0,x1)=γ(x0,x1)=0.716
γ4=0.716>γ1=0.705>γ2=0.672>γ3=0.664.
由结果可知,案例4与目标案例案例的灰色关联度最大,将其加工方案作为目标案例的建议解。将目标案例与案例库中案例进行对比,案例1和案例4尽管在工件尺寸及硬度上与目标案例有差距,但在加工面类型关键属性上,案例1和案例4与目标案例相同,因此案例1和案例4与目标案例的相似度较高。案例4与案例1相比,其在多个属性上与目标案例接近,因此案例4与案例1相比与目标案例更加接近,说明经灰色关联分析后得到的相似案例较为合理。
4.2 切削参数优选实例验证
正交实验是多因素多水平的一种实验方法,可以以较小的试验次数达到较好效果。本课题组使用涂层刀具,在CA6140车床上对经调质处理的45钢棒料进行外圆加工,对切削力、切削温度、表面粗糙度数据进行了采集,获得了16组车削数据,其部分数据如表7所示,完整数据见文献[13].
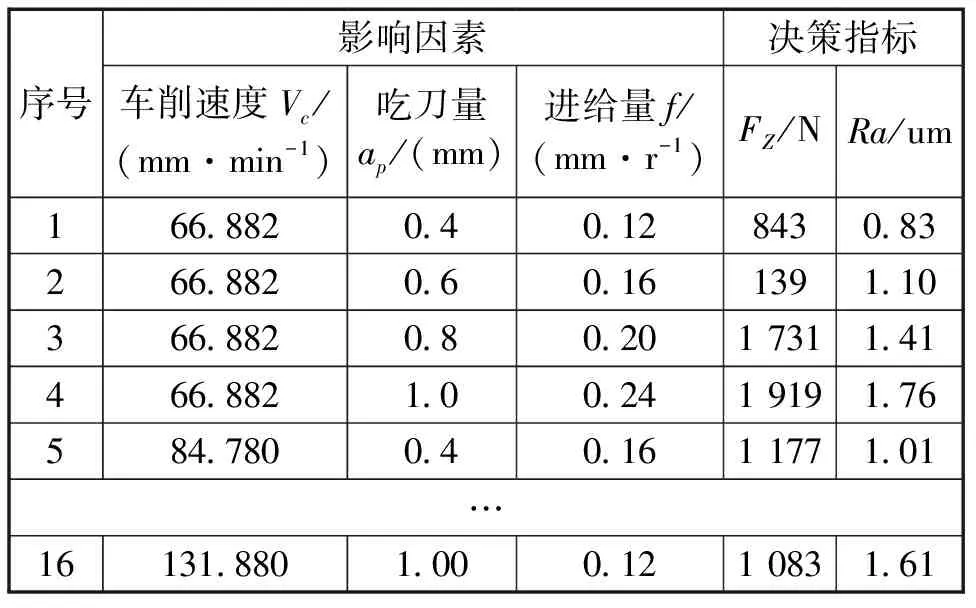
表7 外圆车削试验数据
切削力及加工效率是切削加工中的重要指标,本文以最低切削力G1和最高加工效率G2目标为例,基于VIKOR法对切削参数进行优选。切削力FZ与车削速度VC的方向相同,是切削力分力中最大、对机床能量消耗影响最多的力,是进行切削参数选取时的重要依据和考量。在切削参数中,影响FZ的主要因素为背吃刀量ap,最小的是车削速度VC.所以理想解应为背吃刀量ap及进给量f的最小值,同时为了兼顾加工效率,车削速度选取最大值。根据公式(19)计算三个属性在不同目标下的权值,可得在切削力最小的目标下,切削三要素所占的权值分别为wA1=0.063、wB1=0.702、wC1=0.235.
切削效率可以用金属去除率进行说明,金属去除率如下:
Q(mm3/min)=VC×ap×f
(24)
由金属去除率公式可得,三个变量对于金属去除率,即加工效率具有相同影响。因此,以加工效率G2为目标的切削三要素的权值可以设置为wA2=0.333、wB2=0.333、wC2=0.333.
将切削力G1的权值w1设置为0.7,加工效率G2的权值w2设置为0.3.按公式(20)对三个属性权值进行计算,可得wA=0.15、wB=0.59、wC=0.26,对每个备选方案的贴近度系数CCi进行计算,结果如表8所示。
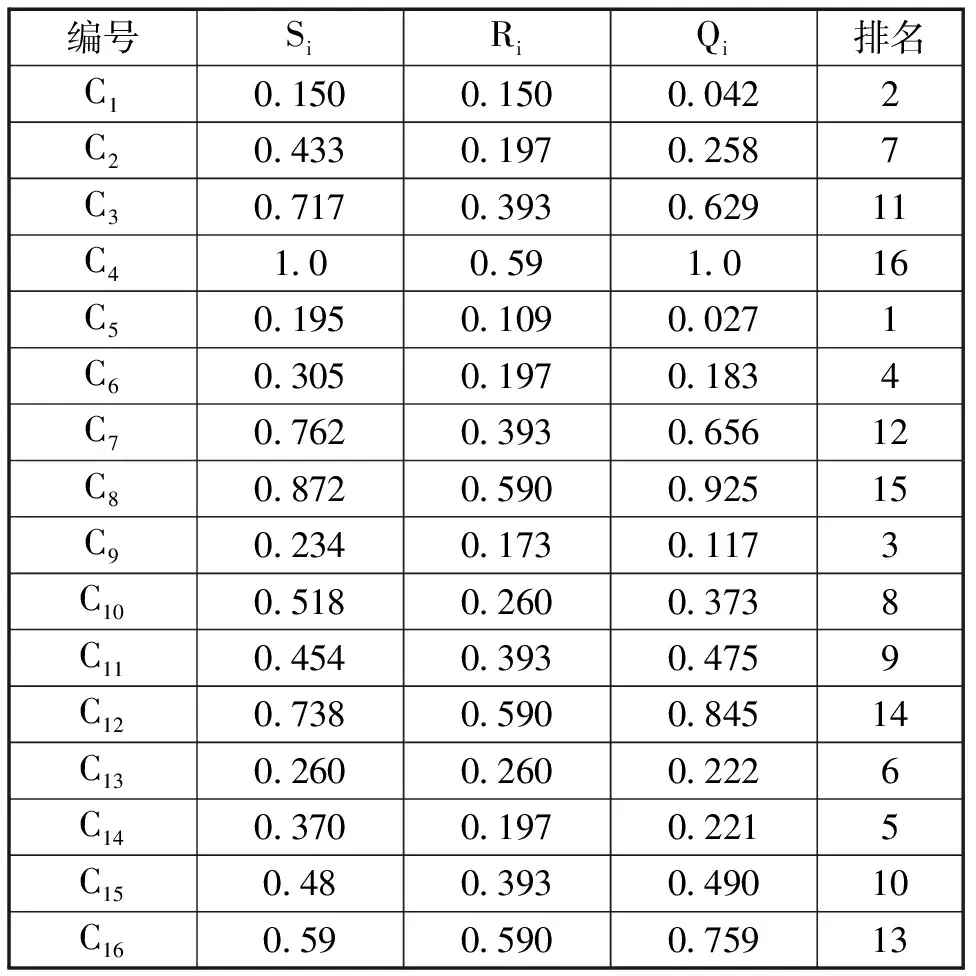
表8 综合指标及其排序
设置妥协系数为0.5经过计算可得序号5及序号1为妥协最优切削参数。通过分析可以看出,在16组切削参数中,第一组切削参数FZ切削力最小,有最好的表面质量;第5组切削参数虽然切削力较第1组稍大,但切削速度高于第一组,效率较高。因此通过妥协排序法将第五组与第一组推荐给用户根据用户的需要对切削参数选用进行抉择是合理的。
5 结论
(1)基于语义计算及灰色关联分析法实现了切削工艺案例的检索。并通过实例,证明了该方法合理可行。
(2)通过案例推理得到的切削参数往往不只一组,需要根据用户不同的目标需求进一步的选取。本文以车削正交实验数据为例,使用VIKOR方法进行切削参数的推荐,通过实例验证所推荐的第1组切削参数有最小的切削力目标;第5组切削参数在切削力目标上略有损失,但是推荐的切削参数的加工效率与最小的切削力组相比提高了1.69倍,证明了经过VIKOR法推荐的切削参数的有效性。

