加工中心主轴关键热敏感点选取与热误差预测*

田春苗,季泽平,郭世杰,b,唐术锋,b,乔 冠,b

(内蒙古工业大学a.机械工程学院;b.内蒙古自治区特殊服役智能机器人重点实验室,呼和浩特 010051)

0 引言

热误差是影响机床精度的关键因素[1-2],约占总误差的40%～70%[3-4]。高精密伺服系统的应用,使得控制误差的影响明显降低。直线电机和高速电主轴技术的应用以及机床零件的制造与装配精度的提高,使得几何误差得到有效控制[5]。然而,随着机床精度的提高,热误差对精度的影响尤为突出[6]。主轴作为机床的核心部件,同时也是机床主要发热部件,其在热误差中占比最大,因此如何抑制主轴热误差的影响,对高精度数控机床的发展具有重要意义。

近几年,国内外研究人员针对主轴热误差补偿技术进行了大量研究[7]。热误差建模是主轴热误差补偿的核心,主轴热误差预测模型的准确性是后续热误差补偿的前提条件。为此,研究人员在热误差建模领域进行了大量的研究,并取得显著成果。其中最小二乘法(LS)、多元线性回归(MLR)、支持向量机(SVM)、BP神经网络、卷积神经网络(CNN)和循环神经网络(RNN)等网络被大量应用于热误差预测模型的建立[8-14],以上方法均能表征温度与热误差之间的复杂关系。LS和MLR等传统建模方法适用于结构简单且精度不高的数控机床的温度与热误差的关系表达,传统建模方法无法处理复杂机床热误差的非线性特征。因此,机器学习就成为了热误差建模的主要方法。其中,SVM、BP神经网络以及循环神经网络等模型需要确定参数才能准确进行预测,因此大量研究使用优化算法进行参数寻优,进而提高模型预测精度[15-21]。广义回归神经网络(GRNN)与这些模型相比,具有更强的全局寻优能力,并且能够较快的收敛,但需要确定最佳模型参数才能挖掘出广义回归神经网络的性能优势。

针对上述问题,本文提出使用K-medoids聚类分析方法对温度测点进行分组。同时为了减少温度传感器个数,避免温度测点间多重共线性问题,使用灰色关联分析计算各测点与主轴热误差之间的相关程度,并从各类簇中,挑选一个相关程度最大的测点作为最佳热敏感点。提出基于ABC算法GRNN网络的热误差预测模型,利用ABC优化算法对GRNN模型参数及光滑因子进行调节,使GRNN模型性能能够完全体现。使用ABC-GRNN模型构建主轴温度场与热误差之间的非线性映射关系。基于实测数据,验证模型预测能力。

1 主轴热误差建模方法

在进行主轴温度场信息获取时,通常需要布置大量的温度传感器,但过多的温度传感器之间会产生多重共线性,影响后续预测模型的预测精度,同时因输入数据较多,也会导致模型训练速度降低。过少的温度测点则不能有效表征出主轴温度场信息。因此为了合理挑选温度测点,本文使用K-medoids聚类算法对温度测点进行分组,并计算各温度测点与主轴热误差之间的灰色关联度,进而挑选出最佳热敏感点。

主轴温度场信息与主轴热误差之间一般为非线性关系,并且各变量变化缺乏规律性,难以通过具体函数进行表征,为此本文提出使用GRNN模型建立温度变量与热误差之间的非线性关系,并使用人工蜂群算法对GRNN网络光滑参数进行修正,解决其易陷入局部最优解和收敛速度慢等缺陷。

1.1 基于K-medoids聚类的温度测点分组

K-medoids算法与K-means聚类算法均是基于划分迭代求解的聚类分析算法,不同之处在于,K-means算法以均值为质心,K-medoids算法在确定平均值之后会选取与之最近的实际温度测点作为质心。因此K-medoids算法针对噪声数据更具包容性。当然,与K-means算法相同,K-medoids算法的初始聚类中心仍是随机选取的。设温度样本为T={T1,T2,…,Tn},T中每个对象称为样本Ti(i=1,2,…,n)。其中每个对象n都有m个维度属性。K-medoids算法将数据集T中的n个对象依据相似性原则和最小化目标函数划分到K个簇中。

聚类算法具体步骤为:

步骤1:确定聚类数K。K-medoids算法的聚类簇数K一般通过经验设置,但缺乏理论基础,同时聚类簇K的不同直接影响后续的聚类结果。为此本文采用手肘法确定最佳簇数,即以最大拐点处对应的簇数作为算法最优K值:

(1)

式中:p表示类簇Ci中的温度测点,m表示各类簇的聚类中心。

步骤2:选择初始聚类中心。随机选取温度样本集T中的温度测点作为初始聚类中心。

步骤3:计算剩余温度样本中的样本对象到初始聚类中心Tu的欧氏距离D:

(2)

式中:j=1,2,…,m(m为测点中温度数据);Ti,j表示温度样本Ti中的全部温度数据;Tk,j表示初始聚类中心Tk中的全部温度数据。

步骤4:增加与初始聚类中心距离最远的温度样本成为下一个聚类中心的概率。

步骤5:重复步骤3和步骤4,直至选出K个初始聚类中心。

步骤6:计算剩余温度样本至每个初始聚类中心的欧氏距离:

(3)

步骤7:将各温度样本分配到与之欧氏距离最近的聚类中心的簇中。得到K个类簇{C1,C2,…,Ck}。计算非质心样本到当前聚类中心的距离之和,将该值最小的样本,作为新的聚类中心:

(4)

步骤8:重复步骤6和步骤7直至聚类中心的位置不再发生改变。

1.2 温度热敏感点提取

通过K-medoids聚类算法进行分组后,还需解决多重共线性问题。为此,本文采用灰色关联分析计算各温度测点与五项主轴热误差之间的关联程度,并在每一簇中选择一个温度测点作为热敏感点。

灰色关联度与数据本身初始值无关,仅与样本之间几何变化相识度有关,即温度测点与热误差之间形状变化趋势越相近,表明两者相关程度越高,反之则表明两者相关程度越低。本文选用灰色绝对关联分析计算各温度变量与主轴热误差之间的相关程度,其计算公式为:

(5)

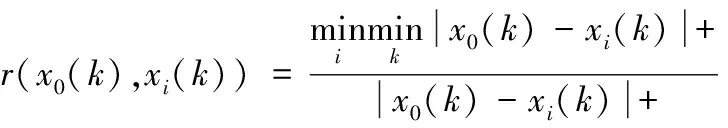
(6)

式中:ρ表示分辨系数,ρ∈[0,1],通常情况下ρ=0.5。

通过温度样本和主轴热误差的灰色关联分析结果可确定各类簇中的最佳温度热敏感点。即在各类簇中挑选一个与热误差关联程度最大的温度测点作为最佳温度测点。有效解决了温度测点间多重共线性对热误差模型预测精度影响。

1.3 GRNN网络建模

GRNN神经网络是径向基网络的一种变形形式,与普通径向基网络相比增加了求和层,这使得GRNN网络具有更好的非线性映射能力和更快的学习速度。其网络结构如图1所示。由输入层、模式层、求和层和输出层构成。

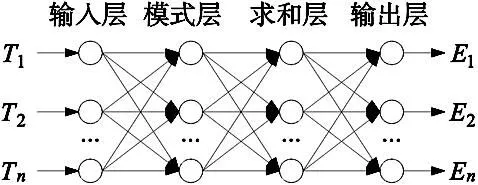
图1 GRNN网络结构图

GRNN神经网络主要进行非线性回归分析,设f(x,y)为随机变量x和y的概率密度。x的观察值为xt,则条件均值计算公式为:

(7)

未知概率密度函数的非参数估计计算公式为:

(8)

式中:n为总样本数,q为x的维度,σ为光滑参数。

将f(xt,y)代入条件均值计算公式中,同时交换积分与求和的顺序:

(9)

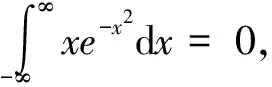
(10)

GRNN模型各层神经元个数及计算流程如下:

步骤1:输入层。输入层神经元个数与训练样本输入向量维度相等,即通过K-medoids聚类分析和灰色关联分析后选取的温度向量。

步骤2:模式层。模式层神经与温度样本数量相等。模式层传递函数公式为:

(11)

式中:T表示模型输入的温度样本,Ti表示i神经元对应的学习样本。

步骤3:求和层。求和层计算方式有两种,一种为分母求和,即对所有神经元输出进行求和,传递函数如式(12)所示。另一种为分子求和,即进行加权求和,将模型层第i个神经元与第j个神经元相加,传递函数如式(13)所示。

(12)

(13)

步骤4:输出层:输出层神经元个数与机床主轴误差项相等,输出层计算公式为求和层两种求和结果相除:

(14)

1.4 ABC-GRNN热误差建模

GRNN模型的非线性映射能力较强,但模型仍存在易陷于局部最优等缺陷。为进一步提升预测精度,本文对其缺陷进行改进,使用人工蜂群优化算法对GRNN模型参数进行调节,同时对光滑因子进行修正。进而实现全局寻优,充分挖掘模型性能。

ABC-GRNN算法实现的原理是:将GRNN网络的参数和平滑因子赋值与ABC算法的食物源中,蜂群中主要包括引领蜂、跟随蜂和侦察蜂3个集群构成。首先由引领蜂搜寻蜜源信息,并以较好蜜源作为初始蜜源,同时进行跟随蜂的招募。引领蜂与跟随蜂的数目相同,其作用是使模型在训练时快速收敛。跟随蜂作为引领蜂的附属,其与引领蜂共享蜜源信息,并将搜寻的新蜜源与引领蜂标记的初始蜜源进行比较。此过程正是算法局部寻优的过程。算法的最后是由侦察蜂进行全局寻优,避免算法陷入局部最优,每迭代一次,侦察蜂的数量都会加一,直至满足终止条件选出最优参数。基于ABC-GRNN网络的主轴热误差模型的预测流程如图2所示。

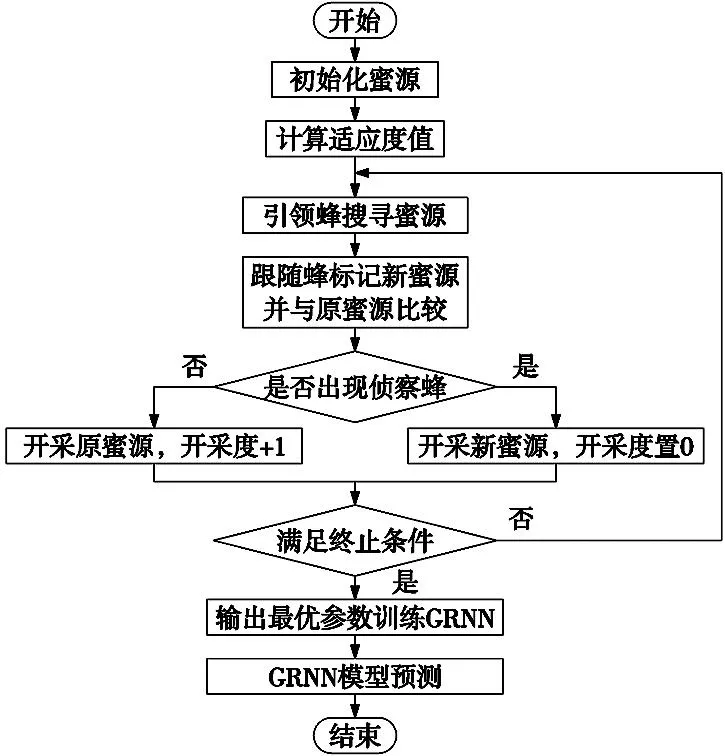
图2 基于ABC优化GRNN网络流程图

基于ABC-GRNN的主轴热误差预测模型具体步骤如下:

步骤1:初始化网络。初始化GRNN网络的参数及平滑因子,并将待优化参数赋值于蜜源。初始化人工蜂群算法,设蜂群中蜜蜂总数为Nz;引领蜂数量为Nc;跟随蜂数量为Ng;蜜源数量为Np;控制参数为Limit;随机初始解为xi(i=1,2,…,Np)。由随机初始解构成D维解空间,即GRNN网络需要确定的参数。初始解在[-1,1]之间取值。

步骤2:计算初始解的适应度值。

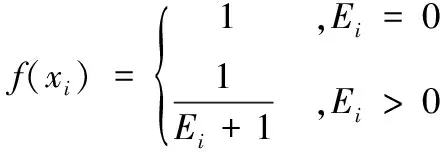
(15)

式中:Ei为误差均方值,即算法性能评价指标,其计算公式为:

(16)

步骤3:引领蜂搜寻新的蜜源,其计算公式为:

(17)

式中:θij为[-1,1]之间的随机数,θij取值较大时,算法会跳出局部最优进行全局寻优,θij取值较小时,搜索能力增强。因此理想的模型为θij值由大变小。为此,本文引入调节因子G,即在每次迭代后减小的θij值。

步骤4:将新搜索到的蜜源与初始蜜源进行比较,保留适应度较高的解:

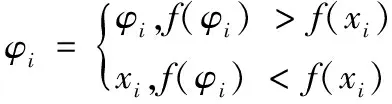
(18)

步骤5:计算当前蜜源的可能值Pi:

(19)

式中:f(xi)为第i个蜜源的适应度值,跟随蜂依据Pi值进行新蜜源的搜索。

步骤6:当蜜源xi更新达到极限值Limit时仍为找到新的替代蜜源时,由以下公式生成新蜜源将其替换:

xi=xmin+a(xmax-xmin)

(20)

式中:a为取值在[0,1]之间的随机常数。

步骤7:若满足最优解条件或达到迭代次数,寻优结束。反之转入步骤3。

步骤8:将ABC算法获取的最优参数和平滑因子传输至GRNN模型中。

步骤9:更新GRNN模型参数,以实际采集主轴温度和热误差数为基础,依据1.3小节训练流程训练ABC-GRNN主轴热误差预测模型。

2 实例分析

2.1 主轴热误差测量

本文以VDL600-A立式三轴加工中心为研究对象,依据ISO230-3[23]标准对机床主轴热误差进行测量。位移传感器Z与主轴轴线方向平行放置。位移传感器X1、X2轴线与X轴平行放置,位移传感器Y1、Y2轴线与Y轴平行放置。安装好位移传感器后,首先采集主轴相对位移,之后通过五点辨识法,将位移数据转换为机床主轴五项误差值。位移信息为矢量,因此当传感器靠近检验棒时,记为负,反之为正。安装方式如图3所示。

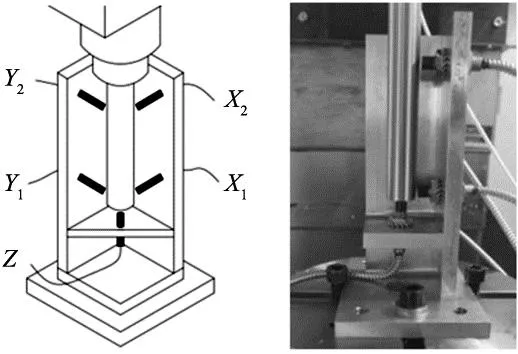
图3 五点法测量示意图

数控机床体积大结构复杂,需布置大量温度传感器,应保证传感器安装和拆卸简便,各个温度传感器数据应协同工作同时采集,以便准确反应出整个温度场信息,同时为保证后续热误差模型的准确性,温度传感器应保证较高的测量精度和稳定性。因此,本文选用磁吸式PT100温度传感器。

在进行温度数据采集前需要布置大量温度传感器,现有温度传感器布置方案往往以研究人员经验为依据,缺乏理论基础。因此为更准确获取主轴温度场信息,本文使用热成像仪对主轴附近温度场进行拍摄。热成像技术是利用红外探测器和光学成像物镜来接收数控机床主轴附近红外辐射能量分布情况,通过呈现的热成像图快速确定主要热源的位置。机床主轴运行270 min的热成像如图4所示。

图4 主轴热成像图

由图4可知,主轴在运行1 h后,主轴电机和轴承附近温度要明显高于周围温度,运行2 h后,各发热区域温度逐渐趋于平稳,达到33 ℃左右,证明此时机床已经达到热平衡。以热成像图的拍摄结果为依据,进行温度传感器的布置,具体安装位置如表1所示。

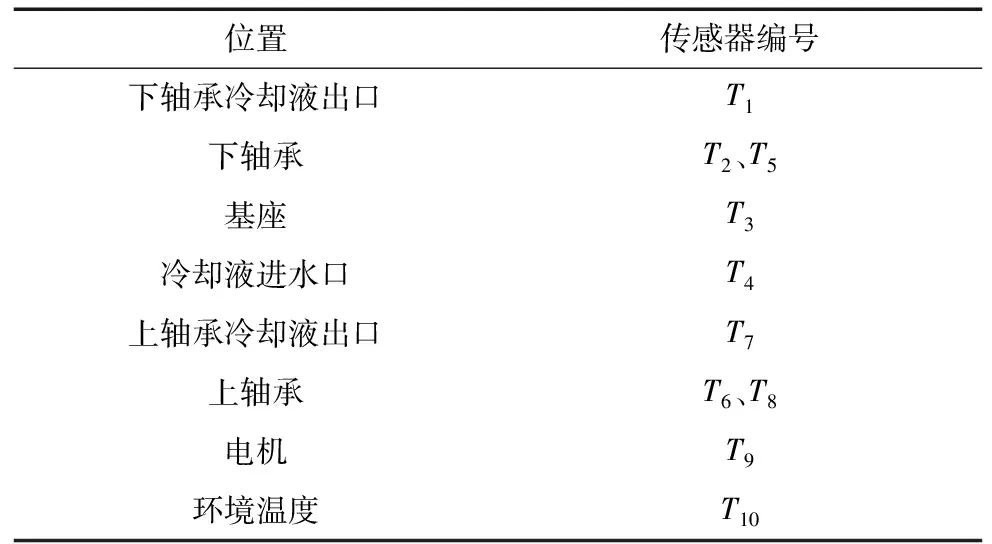
表1 温度传感器分布位置

基于前述温度测点布置策略安装温度传感器,并依据ISO230-3-2020[23]提供的误差测量方案安装电涡流位移传感器。进行温度和热位移数据的采集实验。实验中温度与热位移数据同步采集,采样频率为1 Hz/s。同时保证机床在进行实验前24 h内未进行工作。考虑到在实际的生产中,数控机床可能出现的加工状态,本文分别设计了低速、中速和高速3种恒定转数实验。目的是为了探究不同转速下温度对热误差的影响。试验工况如表2所示。

表2 恒定转数实验设计

2.2 测试结果与分析

实验前数控加工中心已进行24 h自然冷却,温度传感器和位移传感器的安装应确保不影响数控机床的正常运行。实验时应保证主轴温度数据位移数据同步采集。将数据采集硬件系统调试测试完毕后,依据前述试验工况进行数据采集实验。以某次高速试验采集的数据为例进行分析,温度和位移变化曲线,如图5和图6所示。

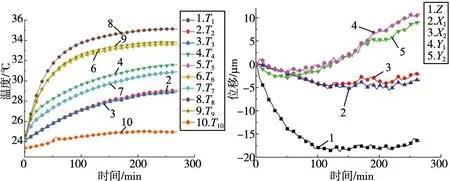
图5 温度变化曲线

由图5可知,温度变化曲线呈上升趋势不断升高,T6、T8和电机外壳T9处温度变化最快,温度最高。这与热成像结果基本一致。各温度测点温度变化速率在前100 min最快,之后变化速度不断降低,在运行至200 min左右趋于平稳,证明此时数控机床达到热平衡。

由图5可知,位移曲线变化规律与温度基本一致。位移曲线在250 min以后趋于平稳状态,相比温度场达到稳态时间稍有滞后。在主轴温度场达到热平衡后,热变形也逐渐趋于平衡,表明了温度与主轴热误差之间有较高的相关性。

3 热敏感点选取及热误差预测

3.1 温度测点优化

本文共进行多组数据采集实验,为了对温度热敏感点选取过程进行详细说明,选用主轴转数n=8000 r/min时采集的数据进行测点优化。T={T1,T2,…,Tn},是待进行K-medoids分析的温度样本数据,其中n=10。对聚类组数K的确定使用第1.1节提出的手肘法。SSE变化曲线如图7所示。当K为4时,曲线拐点最大,因此最佳聚类簇数为4。

图7 SSE变化曲线

K-medoids聚类算法最终将温度测点分成(T1、T4、T7)、(T2、T3、T5)、(T6、T8、T9)和(T10)四组。完成分组后,计算各测点与主轴热误差之间的灰色关联系数。各测点与热误差的灰色关联度如表3所示。

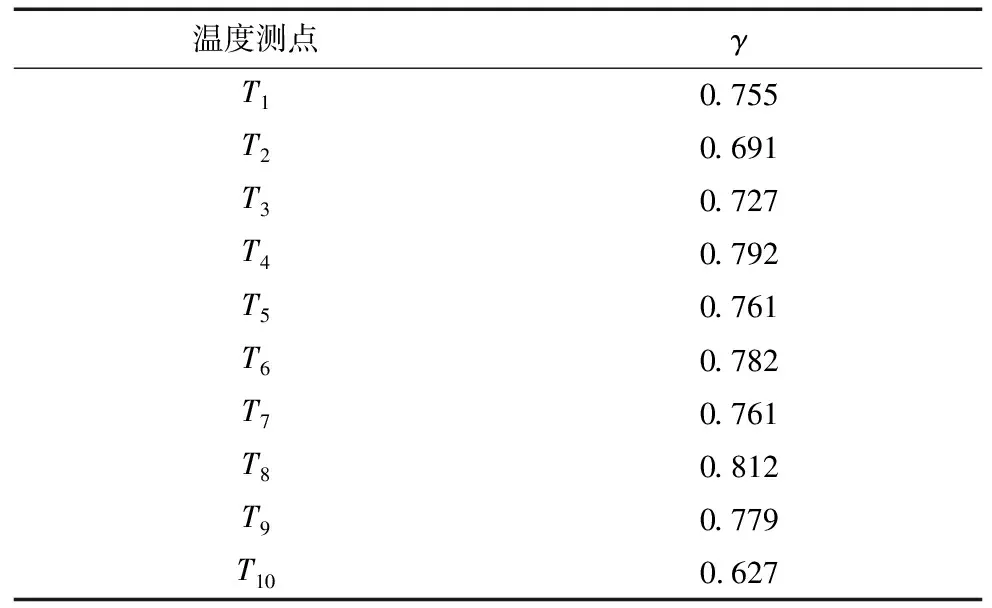
表3 灰色关联度计算结果

依据K-medoids聚类分组和灰色关联度分析,挑选出各类簇中与主轴热误差相关程度最大的温度测点进行后续的主轴热误差建模。最终确定的温度测点为冷却液进水口(T4)、主轴下轴承(T5)、主轴上轴承(T8)和环境温度(T10)。

3.2 模型预测与评价

以第2.2节采集的温度数据和热误差数据作为支撑,第3.1节确定的最佳热敏感点温度变量作为输入,分别使用所建立的GRNN模型和ABC-GRNN模型对主轴沿X、Y、Z轴的热偏移误差δx、δy、δz和绕X、Y轴的热倾斜误差εx、εy进行预测。图8为两种网络模型对以上5种热误差预测的残差。

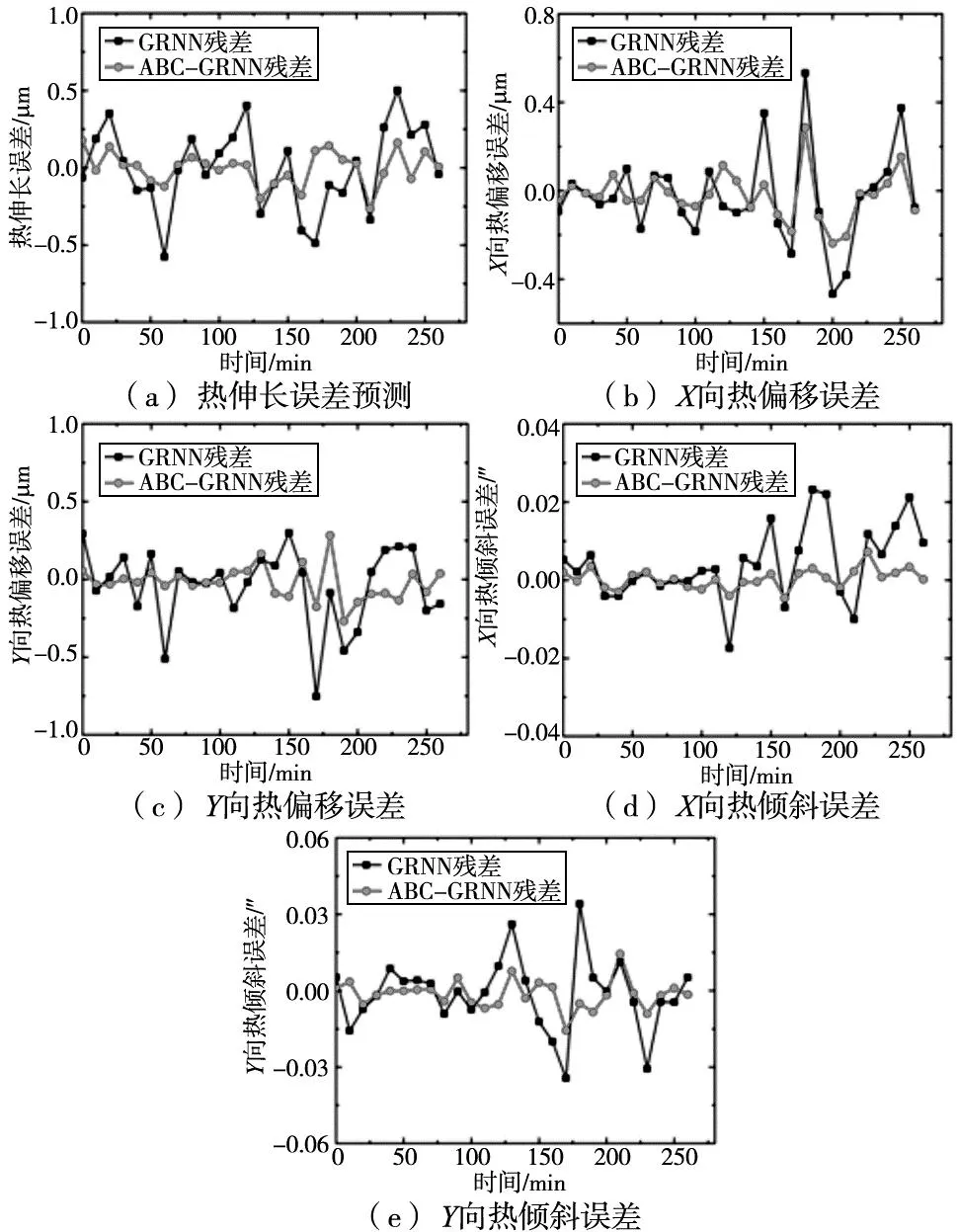
图8 主轴热误差预测残差

由图8GRNN模型和ABC-GRNN模型对主轴五项热误差预测的残差图可知,GRNN模型的残差波动较大,个别预测点偏差跳动明显,说明此时网络参数不是最佳网络参数。使用ABC算法进行调参后,波动明显变小,残差值大幅降低。为了更直观的对比出优化前后GRNN模型的预测能力,以MAE、RNSE和MAPE为依据评价模型拟合优度。优化前后模型拟合优度如表4和表5所示。

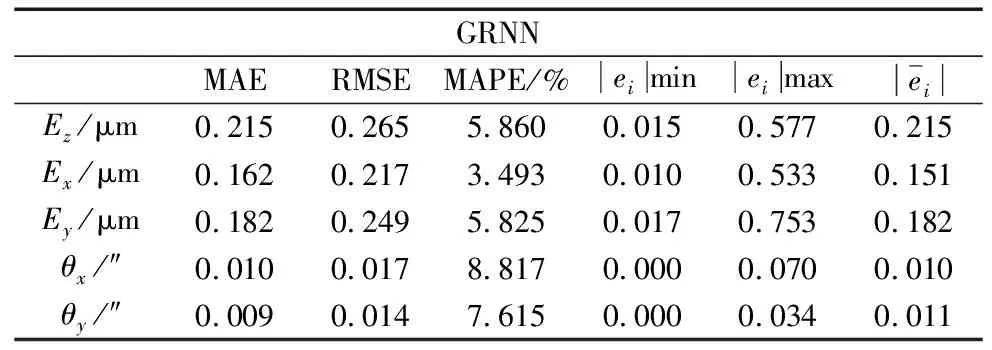
表4 GRNN神经网络拟合优度

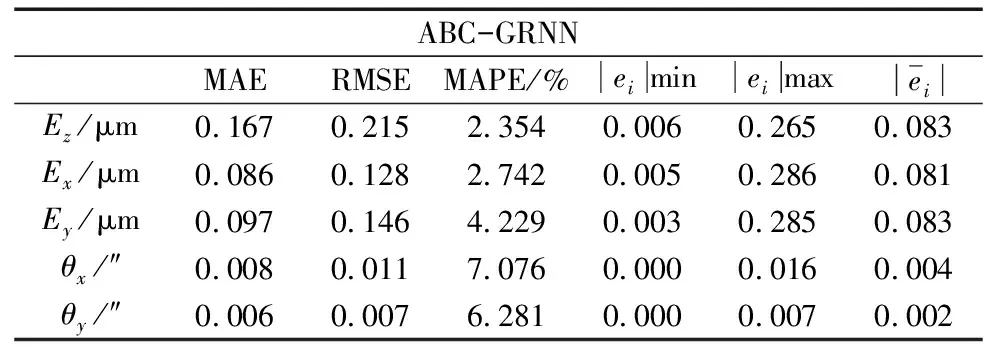
表5 ABC-GRNN神经网络拟合优度

由拟合优度评价表可知,ABC-GRNN模型的预测效果明显优于GRNN模型。ABC-GRNN模型预测结果的MAPE均值为4.536%,对三项热偏移误差预测的残差均值为0.082 μm,对两项热倾斜误差预测的残差均值为0.003 s。GRNN模型预测结果的MAPE均值为6.322%,对三项热偏移误差预测的残差均值为0.183 μm,对两项热倾斜误差预测的残差均值为0.011 s。通过以上分析可知,本文提出的基于ABC-GRNN网络的数控机床主轴热误差预测模型具有更高的预测精度。

4 结论

为解决数控机床主轴热误差对精度的影响,本文针对主轴热误差测量、温度热敏感点选取和热误差建模进行了系统的研究,并进行实验验证,具体研究内容为:

(1)提出了K-medoids聚类分析算法与灰色关联分析相结合的温度热敏感点选取方法。使用K-medoids算法对全部温度变量进行聚类分组。之后通过灰色关联分析深度发掘温度场信息与热误差的关联程度,并依据分析结果,从各类簇中挑选出与相关性最大的测点作为最佳热敏感点。避免了多重共线性对后续建模的影响。

(2)建立了基于ABC-GRNN网络的主轴热误差预测模型。引入调节因子到ABC算法中,提升了蜂群中蜜蜂个体的觅食速度。利用ABC算法准确确定GRNN模型的参数及光滑因子,有效提升了预测模型的收敛速度、全局寻优能力以及预测精度。避免了由经验设置参数引起的随机误差,提升了模型的泛化能力。

(3)依据热成像技术确定温度传感初始安装位置,使用ISO-230-3提供的五点法热误差检测方法测量主轴各项误差值。基于实测数据验证本文提出的主轴热误差预测模型。实验结果表明:使用ABC算法优化后的GRNN主轴热误差预测模型具有更高的精度和鲁棒性。ABC-GRNN模型更适用于确定补偿值。

本文对主轴热误差补偿技术中热误差测量、温度热敏感点选取和热误差建模技术进行了深入研究,为未来热误差补偿提供了理论基础。本文主要关注的研究方法为主轴热误差预测,后续研究中,我们将依据本文所提出理论进行主轴热误差实时补偿。以进一步验证ABC-GRNN模型的可行性。