基于红薯片多孔介质的间歇微波干燥数值分析
满余,童军杰
1(广东工业大学 材料与能源学院,广东 广州,510006)2(广州航海学院 船舶与海洋工程学院,广东 广州,510725)
传统热风对流干燥存在能耗大,干燥时间长以及干燥成品品质不均等问题[1]。为了克服这个缺点,引入间歇微波对流干燥(intermittent microwave convective drying,IMCD)。与对流干燥相比,微波干燥能显著提高干燥效率和产品质量[2-3]。由于传热传质的耦合作用,IMCD中薄片内部水分迁移的机理十分复杂,作为一种相对较新的干燥技术,目前很少有多相流模型来描述这一过程。因此有必要构建IMCD多相多孔介质模型,获得物料内部水分、压力和温度等物性参数的空间分布,为干燥材料提供优化策略。
目前,国内外学者对IMCD的研究方法可分为两大类:基于实验的经验模型[4-6,9]和基于数值模拟的理论模型[7-8]。文静等[9]通过实验研究苹果微波干燥特性与Weibull模型拟合,得到苹果干燥最佳工艺。但由于微波间歇干燥是一个多变量、非线性和时变的过程[10]。经验模型无法对材料内部的传热传质过程提供物理洞察(尤其是回火期间)。以内部水分存在形式和传输机制对理论模型分类,可分为单相流模型[11-12]和多相流模型。单相模型只考虑多孔介质内部的扩散,缺乏多孔介质内部毛细力驱动,对流和蒸发等其他运输机制的影响机理。为了更深入地理解IMCD过程,建立考虑干燥过程中的液态水、气体传输和固体基质的多相流多孔介质模型是极其必要的。CHEN等[13]和MALAFRONTE等[14]分别考虑传热传质以及可变介电特性建立了马铃薯的IMCD多物理场模型,但这些模型都没有考虑到微波功率的间断性,缺乏微波间歇作用下的温度和水分的再分布研究。在YANG等[15]和GUNASEKARAN等[16]提出的微波干燥模型中,分析了微波热源的间歇性,但是忽略了干燥中传质的现象,不能完整地反映实际情况。KUMAR等[7,17]应用Lambert定律,建立苹果薄片IMCD的多相流模型,然而其研究忽略了流场对多孔介质干燥的影响。DEFRAEYE等[18]用苹果薄片CFD模型证明了物料内部干燥动力学显著地受周围复杂流场的影响,流场分布可导致表面传热,传质系数的空间变化。因此,物料外的热质传递影响不可忽略。
针对以上,文章拟开展红薯薄片的IMCD过程分析,考察间歇比(pulse ratio,PR)对微波干燥特性的影响,构建并验证多物理场耦合的红薯薄片IMCD多相流模型。通过比较薄片在2种不同工艺下的干燥特性,以及物性参数变化(水蒸气压力、水分通量、温度等),研究IMCD下多孔介质内水分驱动和热量迁移的机理,以期为红薯干制品的干燥工艺优化提供理论依据。
1 数学模型
图1给出了样品在干燥系统中的布置,以及干燥过程中涉及的传输机制。由于样品内外部热量和质量传递机制不同,分别针对热空气自由流动子域和多孔介质子域建立控制方程。

图1 红薯薄片间歇微波干燥示意图及计算域分解
1.1 问题描述与假设
如图1所示,假设红薯薄片是由固体骨架(s)、液态水(w)和气相(g)三相组成的多孔介质,气相由不溶于固相或液相的空气(a)和水蒸气(v)形成,三相连续且存在局部热平衡。考虑到间歇微波模型的复杂性以及计算成本,应用了以下假设[19-20]:
a)根据代表性基本体积(representative volume element, RVE)的定义,介质被认为是连续和均匀的。
b)在干燥过程中,内部气流呈层流且稳定。
c)薄片内部的初始温度和湿度分布均匀,薄片的热物性和介电性与水分含量相关。
d)干燥过程中薄片不会出现收缩和其他变形。
1.2 控制方程
1.2.1 热空气自由流动子域计算
箱内热空气自由介质遵循流体基础方程,其连续性方程和动量方程分别由公式(1)和公式(2)表示,计算式K如公式(3)所示:
(1)
(2)
(3)
式中:ρg为二元气体混合物的密度,kg/m3;ug为二元气体混合物的平均速度,m/s;p为压力,Pa;t为时间,s;μg为二元气体混合物黏度,Pa·s;I为单位向量。
域中的水蒸气传输由空气流动与自身扩散两部分共同作用,假定扩散现象遵循菲克定律(Fick′s law),以质量守恒定律为基础,由公式(4)表示:
(3)
式中:cv表示水蒸气浓度,mol/m3;Dva表示水蒸气-空气扩散系数,m2/s。等式的第二项是由于气体自身流动传递,第三项是由Fick定律作用的水蒸气扩散传递。
热空气自由流动子域中能量方程如公式(5)所示:
(5)
式中:cp,g为气体比热,J/kg·K;λg为气体导热系数,W/m·K;Q为间歇微波热源和潜热产生的热量变化,W/m3;T为温度,K。
1.2.2 多孔介质子域计算
根据体积平均[21]的思想以及Brinkman方程求解红薯切片内部的压力和速度分布,考虑到多孔介质中存在渗透效应,连续性方程和动量方程需要通过达西定律进行修正,分别由公式(6)和公式(7)表示:
(6)
(7)
式中:ε为孔隙中气相所占的份数,由于部分孔隙内含有液态水,容纳气体的空间取决于初始等效孔隙率φ和气体饱和度Sg的乘积,即ε=φSg;kg为气相固有渗透率,m2;kr,g为气相相对渗透率,m2。
多孔介质子域内水蒸气传质方程如公式(8)所示:
(8)

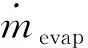
(9)
式中:Kevap为蒸发率,1/s;cv,sat为水蒸气饱和浓度,kg/m3;aw为水活度与水蒸气饱和蒸气压相关,pv/pv,sat(T)。
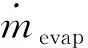
(10)
式中:Dw为液态水有效扩散系数,m2/s。
多孔介质子域内的能量方程由公式(11)~公式(13)表示:
(11)
(ρcp)s,w,g=(1-φ)(ρcp)s+Swφ(ρcp)w+Sgφ(ρcp)g
(12)
λs,w,g=(1-φ)λs+φSwλw+φSgλg
(13)
式中:ρ为液态水的密度,kg/m3;cp,s、cp,w分别为薄片中固体和液态水的比热容,J/(kg·K);λs、λw分别为薄片中固体和液态水的导热系数,W/m·K;γ为蒸发潜热,J/kg;Qm为微波热源,W/m3;f(t)为间歇函数。式(11)最后一项不存在于对流干燥计算中。由于多孔介质内密度,比热容以及导热系数随各相的质量和体积分数变化。因此,采用体积加权平均法对内部热物理性质进行计算,如公式(12)、公式(13)所示。
通过水蒸气浓度cv﹑空气浓度ca以及液态水浓度cw和气相饱和度Sg﹑液相饱和度Sw的关系式求解公式(12)~(13),由公式(14)~(16)表示:
(14)
(15)
cw=ρwφSw
(16)
式中:ca为空气浓度,mol/m3;Ma、Mv分别为空气和水蒸气相对分子质量,kg/mol;R为气体常数,8.314 J/(mal·k)。
根据HALDER等[22]所述,多孔介质内各组分的饱和度之和为1,见公式(17):
Sw+Sg=1
(17)
针对多孔介质内部微波热源计算,采用Lamberts定律计算,目前Lamberts定律已被广泛用于微波加热模型[7,23-24]。该定律考虑了样品内微波吸收的指数衰减,由公式(18)表示:
Pm=P0exp[-2α(h-z)]
(18)
式中:Pm为微波功率,W;P0为表面入射功率,W;α为衰减常数,1/m;h为薄片厚度,m;h-z表示距表面的距离,m。
通过求解体积相同的水所吸收的热量来确定表面入射功率P0,考虑蒸发潜热引起的热量损失,可以得到公式(19):
(19)
式中:mw为液态水的质量,kg。
衰减常数α由公式(20)表示:
(20)
式中:λ为微波在自由空间波长,在微波频率2 450 MHz和空气温度20 ℃的条件下λ为12.24 cm,ε′和ε″分别是介电常数和介电损耗,考虑含水量对介电性的影响。
微波体积热量Qm由公式(21)表示:
(21)
式中:V为样品的体积,m3。
1.3 IMCD干燥条件
在IMCD干燥中,为了获得高质量的干燥产品选择合适的PR非常重要,PR计算如公式(22)所示。在本研究中,考虑了间歇比分别为PR=2,PR=3,PR=4,PR=5的4种工况,如表1所示。在模型中利用COMSOL函数组合来设计间歇函数,其中在加热期间(微波开启期间,ton)间歇函数f(t)为1,回火期间(微波关闭期间,toff)f(t)为0,间歇函数f(t)与能量方程中的微波热源项Qm[公式(11)]相乘,以实现微波热源的间歇。

表1 间歇时间设置Table 1 Intermittencies employed in the simulations
(22)
式中:ttotal表示总干燥时间。
1.4 边界条件
模型出口边界条件设为略高于大气压力,并增加防回流条件,除了干燥箱进出口边界外,其他边界均绝热。热空气自由流子域和多孔介质子域之间的边界上气相速度和压力相等,这意味着速度矢量的分量在自由流子域和多孔介质子域之间的界面处是连续的。同样地,界面上压力连续。通过内部边界条件,耦合N-S方程和Brinkman方程求解。
1.5 初始条件
表2总结了IMCD过程中模型的初始条件以及输入参数的表达式。

表2 数值求解的参数设置Table 2 Parameters and values used for the numerical simulation
1.6 网格划分和稳定性分析
基于COMSOL自定义网格划分选项,采用映射功能分区建立非结构化网格,在物料边界建立10层拉伸因子为1.2的边界层。为了验证模型的准确性,分别针对网格数46 088、80 665、90 084、102 784、120 683以及140 630的IMCD模型进行了网格稳定性分析,如图2所示。针对每个网格数量,测量其出口速度。可以观察到,在102 784网格前,速度值不稳定,从网格数102 784开始,预测速度保持恒定,相对误差小于0.5%,意味着解与网格数无关。因此在模型计算中,选定102 784个网格数进行整个模拟。

图2 网格稳定性
1.7 模型数据验证
本研究采用文献[32]中红薯间歇微波干燥实验数据以及文献[33]苹果间歇微波干燥研究对模型进行验证,分别如图3和图4所示。前者是在相同的间歇周期(5 s微波开启,30 s微波关闭)下,基于单个长×宽为34 mm×5 mm的红薯薄片对干燥模型验证。由图3可得,在干燥早期阶段,求解所得的干基含水量以及有效扩散系数与实验数据显示出较高的一致性;在干燥后期,所提出的模型数据略高于实验数据。经过分析误差产生可以归因于两个主要方面:一是由于在水分迁移的后期过程中,薄片收缩导致水分迁移至表面的距离减少,而本模型没有考虑到薄片的形变影响。二是由于Lamberts定律认为微波功率在物料表面或任意水平面上的吸收是均匀的,但实际干燥过程中由于薄片水分分布不均,功率在薄片表面及其内部分布不均,因此产生了局限性。通过对比薄片内干基含水量以及有效扩散系数随时间的变化,得出模型与实验结果吻合较好,含水量预测曲线对实验值的拟合程度R2达到0.986,有效扩散系数曲线拟合程度R2达到0.98。R2越接近1,模型与实验结果的拟合优度越高[34]。在间歇周期PR=3的条件下,基于单个长×宽为50 mm×20 mm的苹果薄片温度模拟值以及实验值与本模型中相同规格的红薯薄片作对比。由图4可以看出,本研究温度预测值与文献[33]给出结果吻合度较好,皆显示出温度在间歇周期内的波动,每周期内温度偏差值在0.2~10 ℃。由于苹果薄片含水量比红薯薄片高,微波功率作用于物料内水分含量,因此红薯薄片干燥后期温度值较低。

图3 干基含水量及有效扩散系数与文献[32]给定结果对比图

图4 本模型中温度值与文献[33]给定结果对比图
2 结果与分析
2.1 间歇比对间歇微波对流干燥特性的影响
图5显示了在对流热风干燥的工况下,箱内进口侧与出口侧薄片干燥至指定液相饱和度(Sw<0.05)所需的时间。其中薄片样品NO.9满足热风对流从前驻点横掠侧壁,获得对流热量最大,所需干燥时间最少;薄片NO.4受其余薄片尾迹区的影响,所需干燥时间最长。针对多物料烘箱中红薯薄片内部干燥特性的讨论,下文分别以薄片NO.4和薄片NO.9展开。
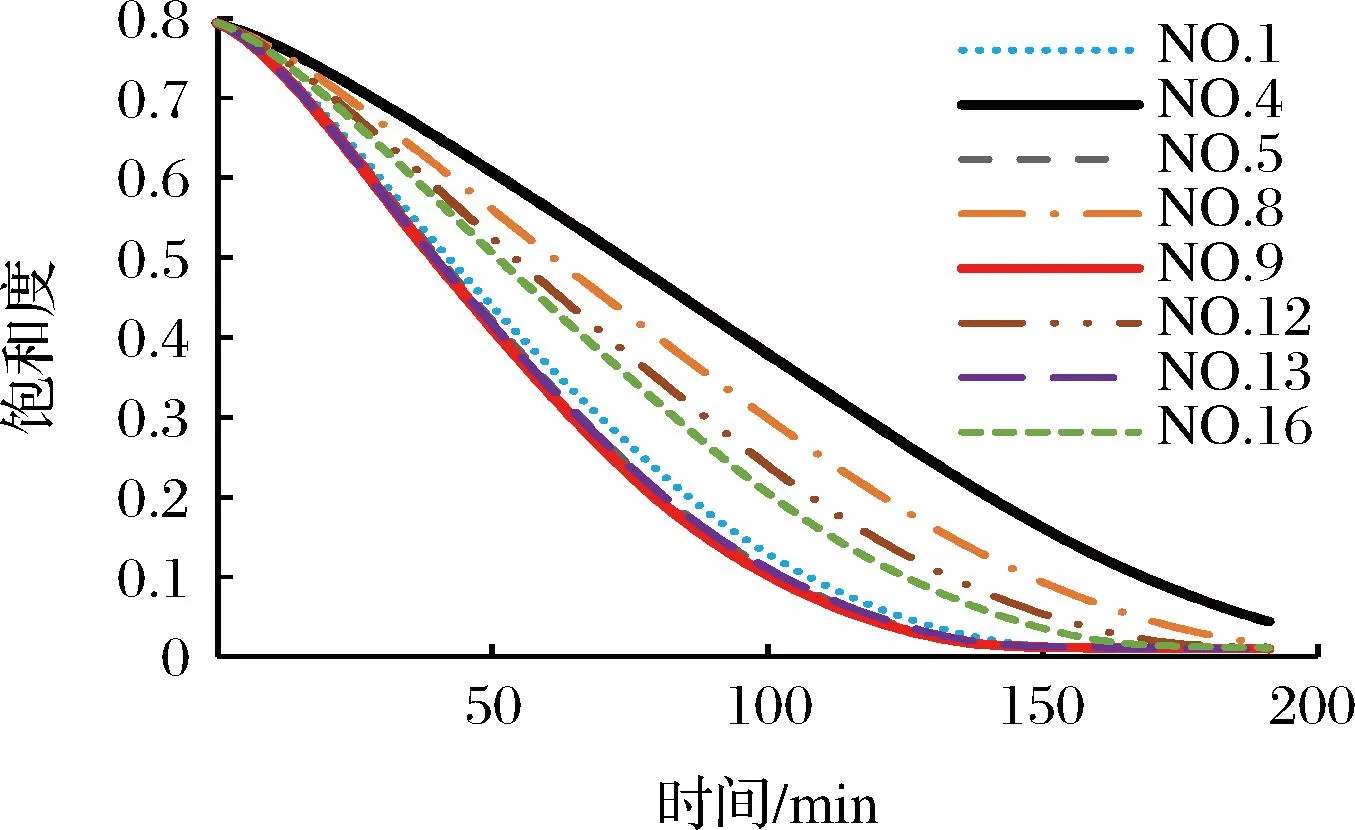
图5 对流工况下进口侧和出口侧薄片液相饱和度随时间变化曲线
基于NO.4薄片,图6显示了不同PR下IMCD和对流干燥下水分比变化曲线,其干燥速率随含水量变化曲线如图7所示。由图6可以看出,随着PR增大,红薯薄片完成干燥的时间延长,当PR为5,水份比降低到0所需时间为90 min;当PR为2,干燥至同样的水份含量所需时间为39 min。由图7可知,IMCD分为加速阶段和降速阶段,在干燥早期阶段,薄片内具有高水分含量,此时间歇微波热源通过加热薄片,使水分快速扩散,水分含量在短时间内显著降低;PR越大,干燥速率越小,PR为2的间歇微波干燥速率是PR为5的1.87倍。

图6 不同PR下薄片NO.4水分比变化曲线
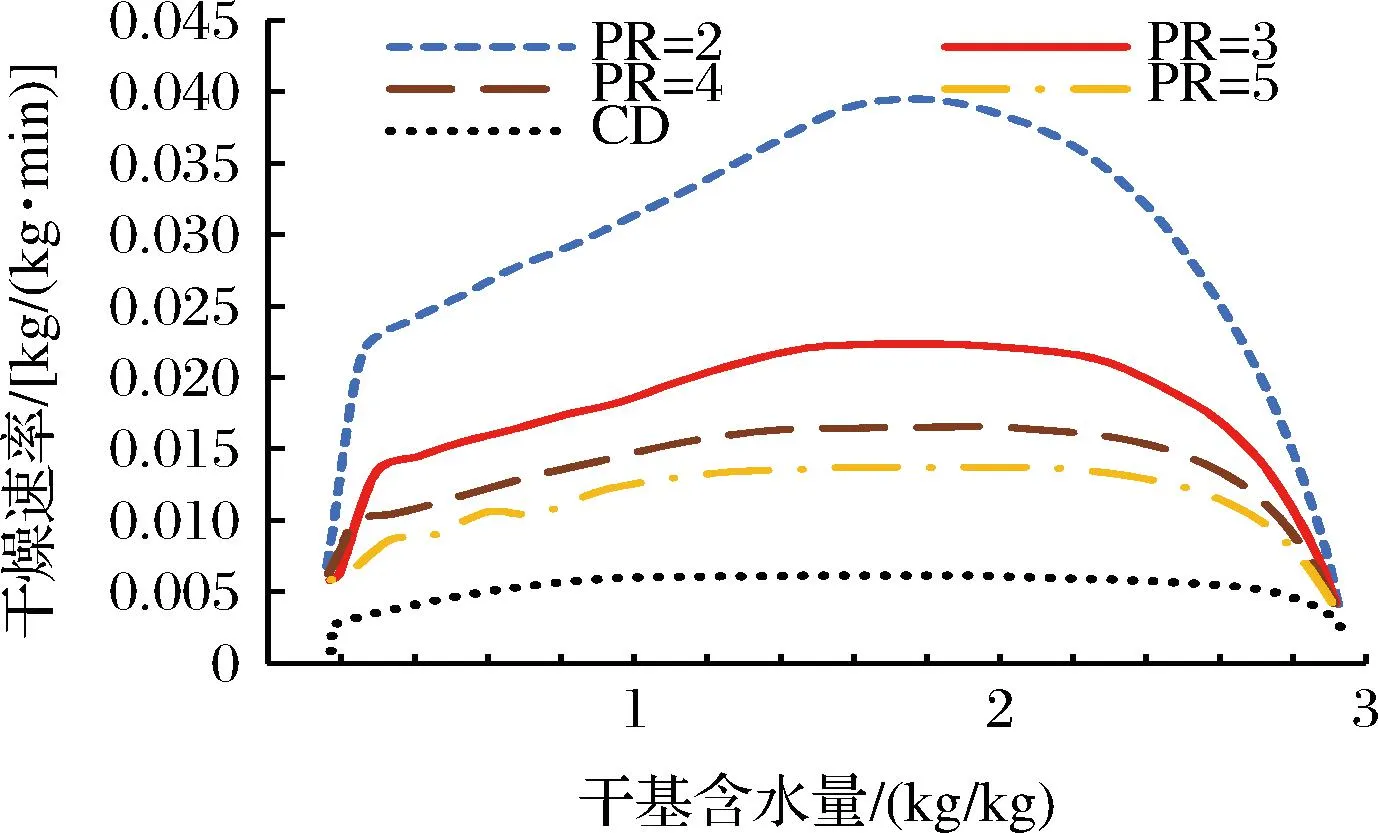
图7 不同PR下薄片NO.4干燥速率随含水量变化曲线
图8显示了NO.9薄片在不同PR下IMCD和对流干燥下温度变化曲线。由图8可看出,IMCD过程中薄片的温度出现波动,在微波开启期间上升,回火期间下降,可以通过改变间歇周期来控制温度的增加和波动。在微波干燥中设置间歇时间这一步骤,可为红薯薄片内部热能和水分重新分配;在回火期间,为薄片内水分向表面扩散提供时间,从而有效防止过热或焦化,保证干燥品质,与采用微波连续加热相比,有效防止薄片干燥过程中升温过快,提高产品质量。当PR过小时,随着干燥的进行,烘箱内NO.9薄片出现局部过热现象,温度达到105.6 ℃,导致产品焦化或褐变。当PR过大时,所需的总干燥时间长,增加干燥能耗,因此本文选取微波开启60 s,关闭120 s的条件下(PR=3),研究红薯薄片多孔介质间歇微波对流干燥特性。

图8 不同PR下薄片NO.9温度变化曲线
由图6~图8可知,在相同的干燥条件下IMCD的干燥进程比对流干燥更快。在干燥60 min后,对流干燥将水分比降低到0.69,而使用PR为3的IMCD将水分比降至0,IMCD显著缩短了干燥时间。通过对流干燥将水分比降低到0需要191 min,是间歇比为3的间歇微波对流干燥的2.2倍。同样地,IMCD将干基含水量降低到1.8 kg/kg的干燥速率是对流干燥的2.63倍。由于微波能量通过时变电场和磁场在空间中传播,穿透薄片以体积热方式干燥物料,与对流干燥相比,IMCD的温度高出9.3~69.3 ℃。这种体积加热导致与温度相关的扩散率,压力梯度以及通量较高(于第2.2节和2.3节提供),特别在干燥的后期,物料表面形成干燥前沿,内部水分迁移至表面蒸发的阻碍增加,由于微波能直接渗透内部的水分中并迅速迁移,因此在热风对流干燥中设置间歇微波热源能实现干燥优化。
2.2 间歇微波干燥下薄片水蒸气压力分布
如图9所示,取薄片NO.4侧壁中点连线线段,考查不同时刻下水蒸气压力沿该线段的空间分布,结果表明薄片内部的水蒸气压力可达到10.8 kPa,呈中心高边缘低的趋势。在干燥初期,由于薄片边缘在热风对流作用下首先失水干燥,其水分浓度低;薄片核心处水分浓度高,由于间歇微波作用于高水分含量处,因此薄片核心处获得的微波能量比边缘处高,导致核心处大量水蒸气蒸发,形成高水蒸气压力分布。边界处水蒸气压力较低更接近于环境压力,使水蒸气更容易被传输到外界。

图9 不同干燥时刻下薄片NO.4内水蒸气压力的空间分布
2.3 间歇微波干燥下薄片多相流通量分布
为了考察间歇微波干燥下物料内部水分通量变化,基于薄片NO.4侧壁中点连线线段,得出由二元气体扩散和对流压力梯度引起的水蒸气总通量空间分布,如图10-a所示。水蒸气总通量Jv由公式(23)表示:

a-水蒸气总通量;b-液态水总通量图10 不同干燥时刻下薄片NO.4内总通量的空间分布
(23)
由图10-a可以看出,在IMCD过程中,高水蒸气通量始终聚集于薄片前沿和后缘0~0.01 m区间内,在此区间内水蒸气通量比中心处高0.02~0.025 mol/(m3·s),呈现表面高中心低的趋势。结合图9分析可知,由于物料前沿和后缘水蒸气压力较低,表面处的水蒸气浓度低,形成较高水蒸气梯度,导致内部水蒸气释放到表面外,产生较高的水蒸气通量。液态水总通量Jw由公式(24)表示:
(24)
毛细扩散和气压梯度引起的液态水总通量如图10-b所示,可以看出,在间歇微波干燥期间,高液态水通量集中在距离薄片表面0~0.01 m。由于IMCD干燥速度和温度高,水分被更快更多得传输到物料前沿和后缘处蒸发,以水蒸气形式释放到干燥环境。干燥至第60 min时,只有核心处存在少量液态水通量,侧壁处通量几乎为0。薄片NO.4总通量随时间变化曲线如图11所示,水蒸气通量和液态水通量因间歇微波热源引起的温度波动而波动。与对流干燥相比,IMCD工艺下薄片内水蒸气通量高出0.37~2.28倍,液态水总通量高出0.67~1.9倍。结合图10,可以得出由于在间歇微波干燥过程中,液相和气相的转换集中于物料的表面处,与对流干燥相比,水分通量高;随着干燥进程,水蒸气和液态水通量的最高点迁移到薄片表面以下,距离表面0.01 m以内,水分扩散到干燥箱所受的限制减小,因此,间歇微波对流干燥能维持着较高的干燥速率。

图11 IMCD与对流干燥下薄片NO.4的液态水和水蒸气总通量比较
3 结论
考虑多物理场的耦合作用,基于多相流模型研究间歇比对红薯薄片多孔介质间歇微波干燥的影响并与热风对流干燥进行对比,研究结果表明:
a)针对4种间歇比(PR=2,PR=3,PR=4,PR=5)下薄片水分比和干燥速率对比得出,红薯薄片间歇微波干燥的最佳PR为3(微波开启60 s,关闭120 s)。IMCD分为加速阶段和降速阶段,PR越大,干燥速率越小,PR越小,箱内薄片温度越高,导致局部过热现象。
b)PR=3的间歇微波干燥模拟结果表明,与对流干燥相比,IMCD可缩短干燥时间68.6%,箱内薄片温度高出9.3~69.3 ℃,提高了干燥速度,实现干燥优化。
c)通过间歇微波热源体积加热的方式来干燥红薯薄片,与温度相关的压力梯度以及水分通量得到提高。在IMCD过程中,水蒸气通量和液态水通量聚集于薄片表面0~0.01 m,降低水分传输到外界的路径。因此,在对流干燥中设置间歇微波热源能促进干燥进程。

