新建并行道路对高铁桥墩位移响应的可靠性研究
唐冕,徐伟宸,宋旭明,李思佳
(1.中南大学 土木工程学院,湖南 长沙,410075;2.湖南省交通规划勘察设计院有限公司,湖南 长沙,410219)
随着我国东南沿海经济发达地区的公路和铁路路网不断完善,在既有高速铁路桥梁附近,新建公路工程与既有桥梁并行的情况愈发普遍。东南沿海地区软土分布广泛,在软土地区新建并行公路会导致以下问题:1) 在软土地基上加载会对软土地层产生影响,引起随时间变化的软土固结效应,影响桥梁结构安全;2) 在软土地基上新建并行路堤时,软土的固结效应对桥梁结构的影响将随时间变化,桥梁结构的安全可靠程度也会随时间而发生变化;3) 不同新建工程所在地区的软土分布以及物理特性不同,引起既有桥梁结构扰动的土体主控参数存在不确定性。因此,有必要对不同软土参数改变下新建公路工程对既有桥梁结构随时间变化的影响进行研究。
国内外学者对软土地区的新建加载工程进行了较多研究。LEHANE[1]采用离心机模型进行实验,探讨了基坑填土的反复加载作用导致的土体横向应力增大对桥梁结构的影响规律。李志伟[2]结合数值模拟方法和现场桩基变形的实测结果,对邻近堆载引起的桩基位移情况进行了研究。董亮等[3]运用Abaqus软件分析了软土地区单侧堆载作用对桥墩的影响。李鹏琳等[4]建立了有限元模型,对桥梁桩基附近的几个特殊截面处堆载面积等因素对桩基变形的影响进行了研究。李梦然等[5-8]基于响应面理论研究了新建桥梁并行和堆载影响下既有高铁桥梁轨道的形位可靠概率。张春宜等[9-12]就软土地基上新建并行道路对既有桥梁时变的影响进行了研究,但研究软土地基上加载对既有桥梁的影响时,没有考虑桥墩等其他桥梁结构和软土地基的固结效应。此外,代汉超等[13]基于改进响应面法对桥梁抗弯刚度进行了修正,但基于响应面方法分析新建工程对既有桥梁结构影响的类似研究较少,且现有研究[14-16]基本都是对特定时间下的响应值进行拟合,无法反映响应随时间变化的特征。
为此,本文作者依托软土地基上某新建道路并行既有沪宁杭高铁连续梁桥,建立考虑软土随时间固结效应的土体-梁-轨道的一体化三维有限元模型,对土层参数进行单因素敏感性分析,筛选出敏感性程度较大的参数,采用BBD试验设计法拟合土体固结前以及土体固结过程中桥墩横向位移变化的时变响应面函数,分析在土体固结不同时间新建并行道路对既有桥墩产生的位移的可靠概率,由此评估在固结作用下,新建并行道路对既有桥墩位移的影响。
1 相关理论
1.1 参数敏感性分析
对参数进行敏感性分析是使自变量在合理范围内变化,计算其对结构的影响程度[17]。结构的响应值为
其中:xi为结构的变化参数,假设结构参数设计值为X*=(x*1,x*2, …,x*m),则结构在参数取设计值下的基准响应值可表示为
由式(1)和式(2)计算得到的系统响应值G和基准响应值G*的差值反映了参数变化对结构响应的影响程度。基于得到的响应值绘制ΔG/G与Δxi/xi(i=1,2,…,m)的关系曲线,其中,Δxi为xi的变化量,ΔG为参数xi改变引起的系统响应值G的变化量,ΔG/G与Δxi/xi的比值即为敏感系数yi:
yi越大,表明基准状态下系统响应值G对xi越敏感。通过比较各参数的yi即可得出各要素的敏感度[18]。这里着重分析各参数中对桥墩位移敏感性较大的参数。
1.2 时变响应面法
传统的响应面法常用的多项式有线性多项式、二阶多项式和高阶多项式等。线性多项式的响应面法拟合效果较差,而高阶多项式不仅计算量大,而且可能导致在样本点区域的外部出现不稳定等问题[19],因此,一般常用带交叉项的二阶多项式,其具体形式如下:
式中:α0、αj、αij分别为常数项、一次项和二次项的待求系数。
在软土地基上新建并行道路时,软土的固结效应对桥梁结构的影响随时间发生变化,时间是需重点考虑的参数之一。采用式(4)可对结构特定时间下的响应值进行拟合,但无法反映结构响应的时变特征,因此,需要对式(4)进行修正。对于既有桥梁结构,土体固结过程中桥墩位移响应是一个随时间而发生变化的动态过程,试验参数的灵敏度也随时间发生变化。参考马小兵等[20]提出的函数,建立如下形式的时变响应面函数:
式中:f(xi,t)为结构响应值对参数xi的敏感性程度随时间的变化函数;f(t)为响应值随时间变化趋势的函数。式(5)通过添加参变量与时间的耦合函数来反映系统响应值对试验参数敏感性程度随时间变化的特性,可以充分考虑时间与试验参数对响应的共同作用效应,也决定了响应面函数的复杂程度。
1.3 可靠概率分析
用基于时变响应面法拟合得到的响应面函数来替代结构极限状态方程,需对桥墩的位移可靠度进行分析。在工程领域中,蒙特卡罗方法可以用于分析较复杂的结构,且计算结果具有较高的精度,能作为精确解来检验其他可靠度算法的准确程度。但考虑土体固结效应的桥梁结构变形时相关影响因素太多,响应面函数为高度非线性的隐式函数[15]。针对上述情况,在求解既有桥梁结构变形时变可靠指标的过程中,将响应面法与蒙特卡洛法相结合,以解决功能函数不确定的可靠性分析问题。
对结构进行可靠度分析时,需要明确参数类型以及参数的概率分布特性。根据文献[21],软土的回弹曲线斜率κ、临界状态斜率M和压缩曲线斜率λ等参数服从正态分布或者对数正态分布。
蒙特卡罗法依据大数定律,通常需要生成足够多的试验样本点来进行模拟以提高结果的精度,计算量较大。故本文采用MATLAB软件进行抽样统计和计算分析,通过循环代入多组随机试验参数组合进行计算,累计失效次数并计算失效概率,使得蒙特卡洛法的计算过程更加高效便捷。具体步骤如下。
1) 建立结构功能函数Z=g(x1,x2,…,xn),其中,X=[x1,x2,…,xn],为服从概率分布的随机试验变量。设计N个随机变量组合xj=[xj1,xj2,…,xjn],其中,j=1,2,…,N。
2) 将第j组试验数据xij代入Z=g(x1,x2,…,xn)中,得到N个对应值Zj。
3) 当Zj<0时,结构失效。设N充分大时,Zj<0出现了Nf次,则结构的失效概率Pf为
由式(6)得到失效概率,可求得响应面函数计算得到的高铁桥墩位移在某一限值范围内的可靠概率,进而评估新建并行道路对既有高铁桥墩位移的影响。
2 有限元模型建立及敏感性分析
2.1 工程背景
以沪宁杭高速铁路某工点处新建道路并行于既有高铁桥梁工程为背景。该工程位于东南沿海地区,上覆土质较软。既有高铁桥梁为跨度(40+60+40) m三跨连续梁桥,桩基为钻孔灌注桩,桥墩截面为圆端形,桥型布置如图1所示。新建并行道路高度为2 m,宽度为19 m,与既有高铁桥梁的水平距离为25 m。新建道路与既有桥梁的平面位置关系如图2所示。新建道路与既有桥梁并行段位于软土层,参考地勘报告相关资料,土体由上到下依次为杂填土层、淤泥质黏土层、粉质黏土层、强风化花岗岩层和中风化花岗岩层,土层厚度分别为3、12、20、20和65 m。

图1 三跨连续梁桥布置Fig.1 Layout of three span continuous beam bridge

图2 新建道路与既有桥梁的平面位置图Fig.2 Plan location of new roads and existing bridges
2.2 建立时变有限元模型
利用有限元软件Abaqus建立土体、桥梁、轨道于一体的三维有限元模型,见图3。模型土体长×宽×高为200 m×150 m×120 m。模型中土体、桥墩、承台、桩基以及道路结构均采用实体单元,模型中共划分节点31 775个,单元28 800个。其中,土体采用C3D8P线性六面体孔隙流体/应力单元,桥墩、承台、桩基以及道路采用C3D8I线性六面体减缩积分单元,连续梁桥和轨道采用B32型梁单元。
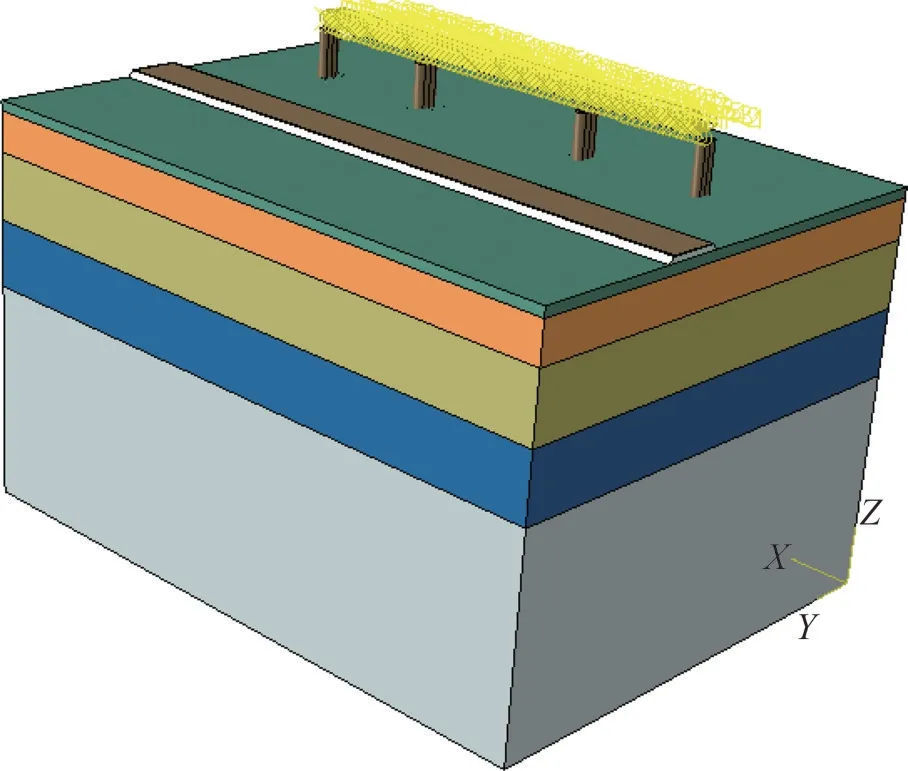
图3 三维时变数值模型Fig.3 Three-dimensional time-varying numerical model
模型中土体与既有桥梁的桩基之间的接触设置为面-面接触,切向定义为小滑动和“罚摩擦”,垂直于接触面上施加“硬接触”。桥墩和梁体之间设置耦合接触,梁体和轨道之间设置弹簧接触。软土层考虑固结效应,采用修正剑桥模型,其他土层采用摩尔库仑模型。模型的边界条件为顶面自由面,底面约束横向及竖向位移,侧面约束水平位移,土层顶面为透水面,土层其余面为不透水面。当孔隙水压力完全消散时,软土固结已经基本达到稳定状态,此时,设置达到稳定状态的依据为土体孔隙水压力随时间的变化速率小于1×10-5kPa·s-1。
2.3 桥墩位移影响因素的敏感性分析
杂填土层厚度相对较小,在参数变量中不予考虑。选用淤泥质黏土层以及粉质黏土层的渗透系数k、压缩应力屈服比K、破坏面帽子曲度β、泊松比v、临界状态斜率M、回弹曲线斜率κ、压缩曲线斜率λ、强风化花岗岩层和中风化花岗岩层的内摩擦角φ、黏聚力c以及弹性模量E等共20个参数作为敏感性分析对象。以这20个参数的设计基准值为依据,依次将单个土层参数折减1%进行三维数值分析,得到既有桥墩在土层参数变化时的位移,将此位移与采用基准值计算得到的位移进行比较,得到不同参数改变对桥墩位移的敏感性系数。土体固结前后土层参数对桥墩横向位移的影响如图4所示,其中,各序号对应的土层参数如表1所示。
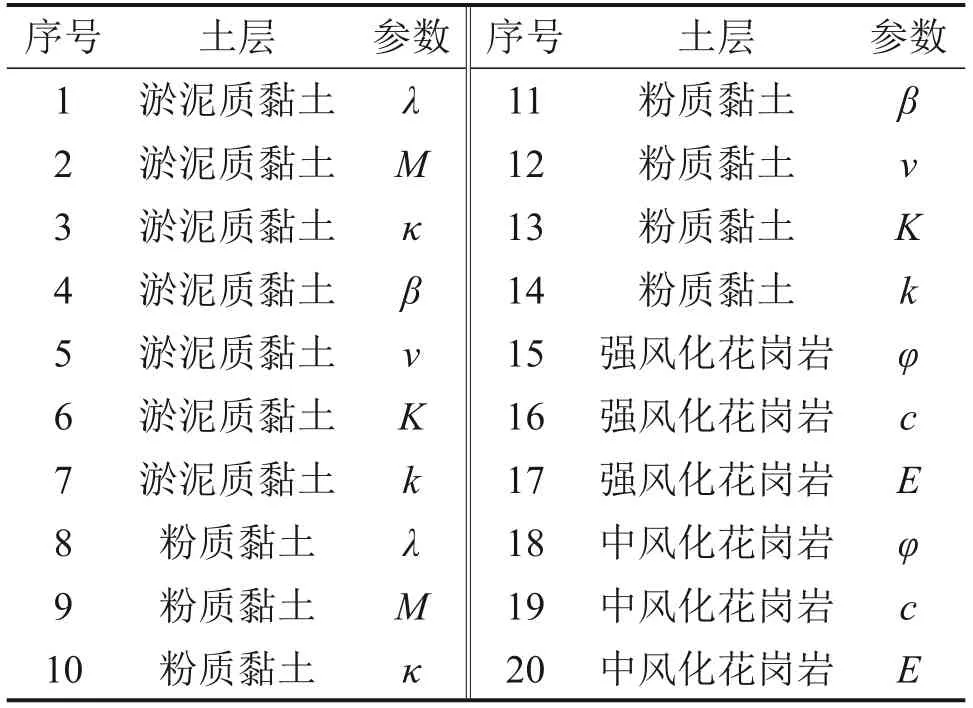
表1 各序号对应土层参数表Table 1 Parameters of soil layers corresponding to each mark
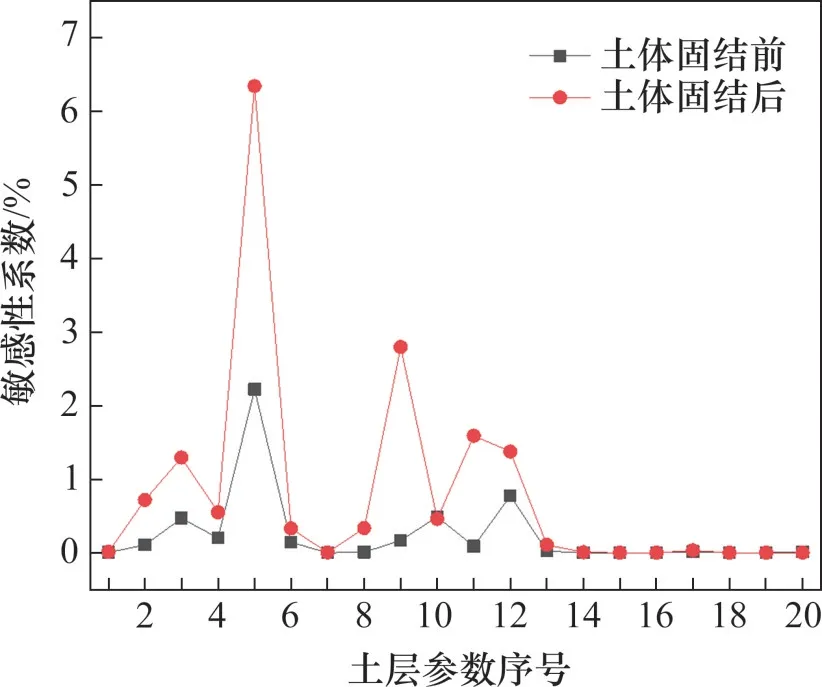
图4 土体固结前后土层参数对桥墩横向位移的影响Fig.4 Soil layer parameters before and after soil consolidation influence on lateral displacement of pier
土体固结前,淤泥质黏土层的泊松比v折减1%时对桥墩横向位移的影响最大,敏感性系数达到2.22;其次为回弹曲线斜率κ,敏感性系数为0.47;粉质黏土层的v和κ折减1%时对桥墩位移的影响较大,敏感性系数分别为0.77和0.49。
土体固结基本稳定后,淤泥质黏土层的v折减1%时对桥墩横向位移的影响最大,敏感性系数达到6.35;κ对桥墩位移影响幅度较大,敏感性系数为1.30;粉质黏土层的临界状态斜率M折减1%时对桥墩位移影响的敏感性系数最大,达到2.80;其次为破坏面帽子曲度β,其对桥墩位移的敏感性系数为1.59。
综合各土层参数变化对土体固结前后桥墩最大横向位移影响及位移增量的敏感性程度,桥墩横向位移对于淤泥质黏土层的泊松比v、回弹曲线斜率κ、临界状态斜率M和粉质黏土层的v、κ、M这6个参数的敏感性较大,故选取这6个参数作为响应面拟合的设计参数。
3 响应面函数拟合
选择敏感性系数较显著的试验参数,依据试验参数和响应值拟合能够较准确地反映所选取的试验参数与响应值之间关系的响应面函数,然后用得到的函数代替原有的有限元模型进行可靠度分析。
3.1 试验设计及函数拟合
采用BBD试验设计方法,对所选取的参数进行六因素三水平设计(即0、-1和+1,分别代表该因素的平均水平、最低水平和最高水平),共生成49组随机样本序列,包括1个中心点(0,0,…,0)以及48个因子点,因素A~F的三水平取值如表2所示。
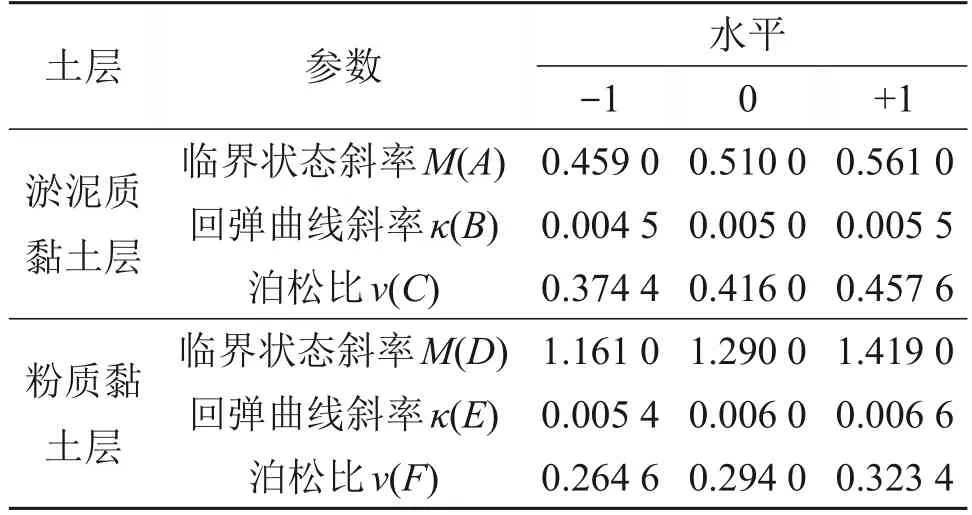
表2 BBD试验设计参数与水平Table 2 BBD test design parameters and levels
采用MATLAB软件对模型计算所得49组土体固结前边墩墩顶最大横向位移进行拟合,通过1个六元二次多项式拟合表示土体固结前桥墩最大横向位移与所选的6个参数之间关系的函数。略去不显著项后,得到的土体固结前桥墩最大横向位移U0的简化多项式方程为
式中:A、B、C、D、E、F的含义见表2。
对模型计算所得49组软土固结作用下的桥墩最大横向位移进行包含时间因素的六元二次函数回归拟合,采用MATLAB软件计算得到系数α随t变化的系数,并略去系数中的不显著项,得到土体固结作用对桥墩横向位移U变化影响的时变响应面方程为
其中多项式系数α表达式为
采用MATLAB软件计算得到系数α随t变化的多项式系数如表3所示,其中缺少的α8、α9等多项式系数对应不显著项,因此表中不罗列。

表3 α随t变化的系数表Table 3 Table of α coefficients varied with t
式(8)中,α0为常数项;α1、α2、α3、α4、α5和α6分别表示对应参数A、B、C、D、E和F与桥墩横向位移U的相关程度,α7表示对应参数A、B与U的相关程度,α10、α12等以此类推。系数α为正,表示桥墩随时间变化的横向位移和对应土体参数之间呈正的相关性;系数为负,则表示呈负的相关性,其数值越大则相关性越强。式(7)中的数值含义同理。
3.2 响应面模型精度评估
这里对响应面函数回归值与有限元模型计算值进行比较,计算所拟合响应面函数的绝对误差以及相对误差,并通过判定系数对拟合得到的响应面模型精度进行检验,判断响应面函数的可靠程度。以表2中各参数范围为依据,随机生成10组试验参数组合,进行响应面函数回归拟合和有限元模型计算,试验参数组合如表4所示。
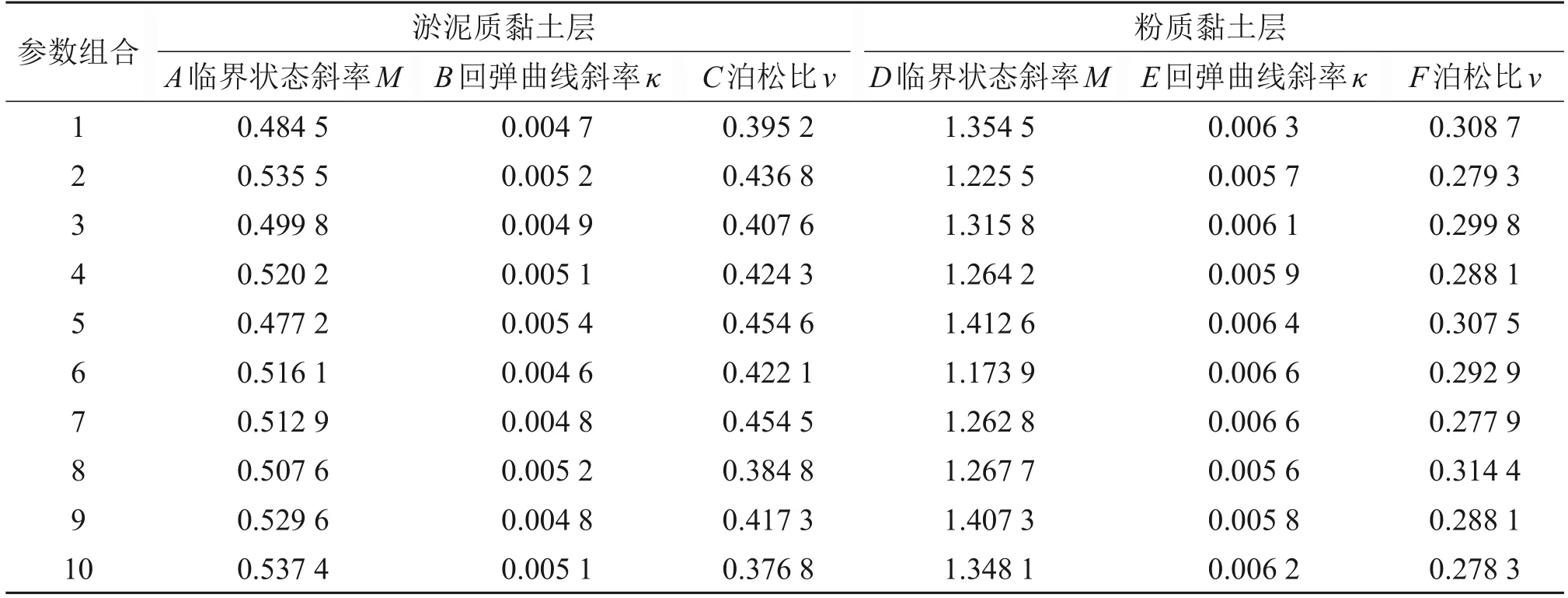
表4 试验参数组合Table 4 Test parameter combination
土体固结前,10个参数组合的桥墩最大横向位移响应面回归值和有限元计算值结果对比如图5所示。

图5 土体固结前桥墩位移计算结果对比Fig.5 Comparison of calculation results of pier displacement before soil consolidation
在土体固结过程中,选取参数组合1~10中前2个组合得到桥墩最大位移处横向位移变化的时变响应面函数回归值和有限元模型计算结果对比,如图6所示。
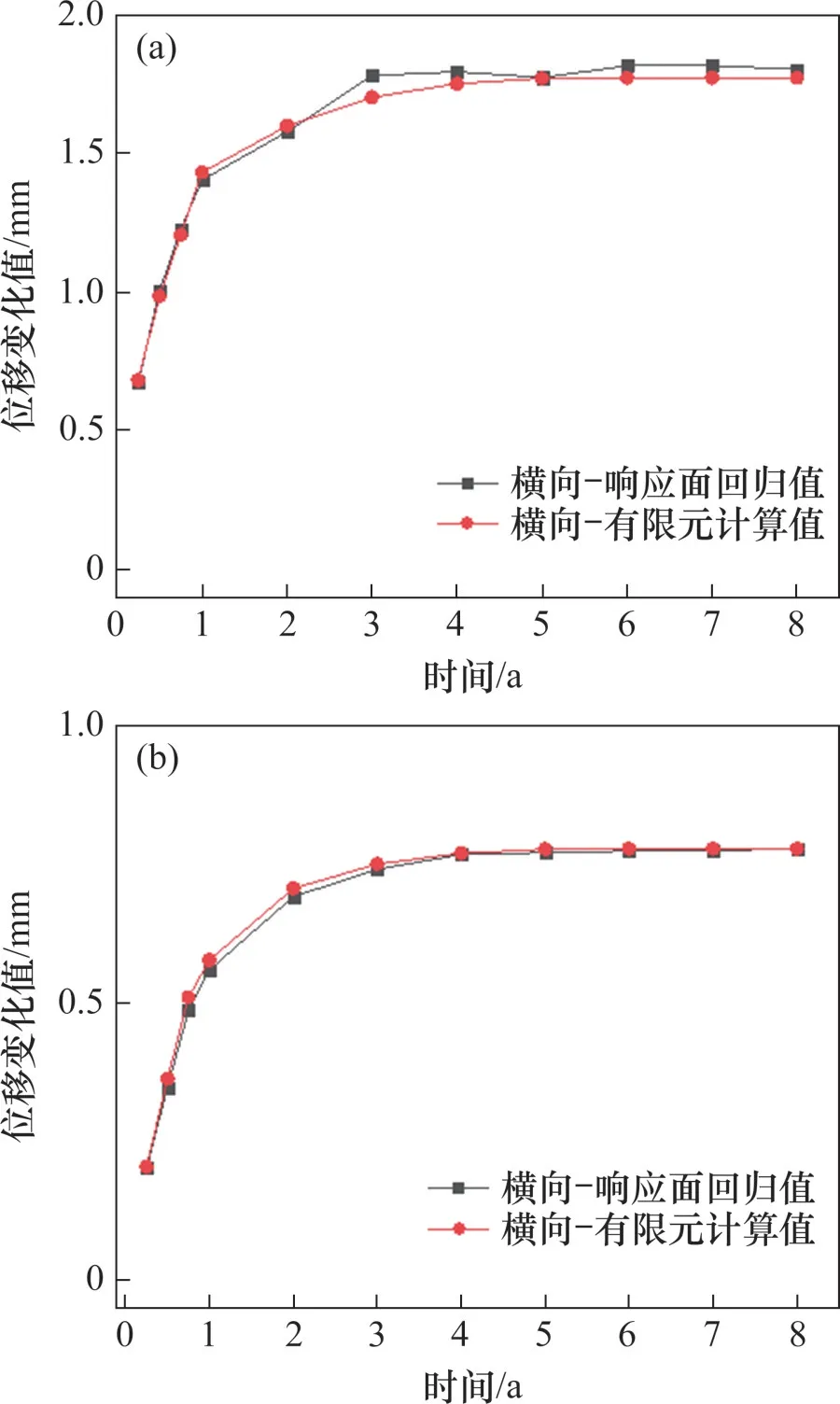
图6 土体固结过程中参数组合1和2桥墩位移计算结果对比Fig.6 Comparison of calculation results of pierdisplacement in parameter combination 1 and 2 during soil consolidation
由图5可以得到:土体固结前桥墩最大横向位移响应面函数回归值与有限元计算值的绝对误差的最大值为0.109 6 mm,相对误差的最大值为4.09%。由图6可以得到土体固结作用下所选2个参数组合在桥墩最大位移处两者的位移变化值绝对误差最大值为0.078 9 mm,相对误差最大值为4.95%。土体固结前及固结过程中桥墩横向位移的响应面回归值和数值模拟结果的最大绝对误差值均小于0.2 mm,最大相对误差均小于5%,可将拟合的响应面函数计算值作为三维数值模拟结果对后续的可靠概率进行计算。
4 可靠概率计算结果
TB 10182—2017《公路与市政工程下穿高速铁路技术规程》[22]规定,在新建工程影响及不限速条件下,无砟轨道墩台顶的位移限值为2 mm。通过MATLAB软件,采用计算参数服从正态分布的normrnd(mu,sigma,[M,N,P,…])语句来生成多个随机试验参数组合,代入通过MATLAB计算拟合得到的响应面函数中,采用蒙特卡罗法进行107次随机抽样,计算桥墩在土体固结前、土体固结不同时间下桥墩最大横向位移小于1、2和3 mm的可靠概率。在计算误差小于20%、置信度为95%时,桥墩横向位移可靠概率随时间的变化如图7所示。

图7 桥墩横向位移可靠概率随时间的变化Fig.7 Variation of reliability probability of pier lateral displacement with time
由图7可知:土体固结前(t=0 a时),既有桥墩最大横向位移小于1 mm的可靠概率接近于0.01%,小于2 mm的可靠概率增大到14.74%,而小于3 mm的可靠概率高达78.22%。这表明固结前大部分横向桥墩位移在2~3 mm之间,部分超过3 mm。由此看出,桥墩横向位移偏大,说明新建路基施工完成后对桥墩最大横向位移的影响较大,小部分超过规范限值。
从图7还可知:土体从开始固结到固结基本稳定(即t=8 a),桥墩最大横向位移小于1 mm的可靠概率为45.60%,小于2 mm的可靠概率增大到80.53%,小于3 mm的可靠概率达94.90%,这说明随着土体固结时间增大,桥墩最大横向位移不断减小,桥墩在横桥向出现了“回缩”的现象,土体稳定后,大部分桥墩的横向位移基本保持在2 mm以内。
5 结论
1) 土体固结前,淤泥质黏土层的泊松比v和回弹曲线斜率κ折减1%时,桥墩横向位移的敏感性系数分别为2.22和0.47,粉质黏土层的v和κ的敏感性系数分别为0.77和0.49。土体固结基本稳定后,淤泥质黏土层的v和κ的敏感性系数分别为6.35和1.30,粉质黏土层的临界状态斜率M和破坏面帽子曲度β的敏感性系数分别为2.80和1.59。土体固结前及基本稳定后,软土层的v、κ和M对桥墩位移的影响较大,其中,敏感性程度最大的参数为淤泥质黏土层的泊松比v。
2) 通过49组有限元模型计算得出土体固结前及固结作用下既有高铁桥墩的墩顶横向位移的六元二次响应面函数,响应面函数计算出的回归值和有限元模型计算结果的最大绝对误差均小于0.2 mm,最大相对误差均小于5%,时变响应面函数可以代替有限元模型进行可靠度分析。
3) 新建并行道路施工后对既有桥墩横向位移有较大影响,横向位移随着土体固结时间不断减小,最终大部分桥墩的横向位移基本保持在2 mm以内。
4) 通过时变响应面函数拟合有限元计算结果,可以极大地提高有限元模拟的计算效率,方便地获得考虑软土随时间变化的固结作用时既有高铁桥墩横向位移计算结果的可靠概率,为类似新建并行工程预测既有高铁桥墩横向位移提供了一种新的估算方法。

