基于蒙特卡洛法的小型水利工程不可预见费测算
詹志琴
(新疆新水水力科技发展有限公司,新疆 乌鲁木齐 830002)
水利工程在施工过程中受到来自外部、内部等诸多方面的影响,经常发生不可预见事件,严重阻碍了工程的进度和质量[1]。因此,有必要在项目前期预留出部分资金应对不可预见事件的发生,这部分资金就是不可预见费用。预留出合理的不可预见费用对水利工程的顺利实施以及提高其造价准确性具有重要的作用[2-3]。然而小型水利工程具有临时性、造价低以及施工管理随意性等特点,其不可预见费用的计算不宜套用现行的水利工程定额计算标准。因此,对小型水利工程不可预见费的取费标准进行探讨就具有较强的现实意义[4-5]。
尽管有不少的专家学者在不可预见费方面作出了大量的研究,取得了丰富的成果,然而由于不可预见事件的发生具有偶然性,可以参考的数据也比较少,无法进行数值的分析与计算[6-7]。基于此,本文决定采用蒙特卡洛理论对小型水利工程不可预见费进行测算。其原理为利用随机数发生器模拟出可供使用的数据,扩大样本数据数量,以达到提高计算准确性的目的。最终为小型水利工程不可预见费的测算提供新的思路和方法。
1 影响小型水利工程不可预见费因素测算模型
1.1 影响因素分析
小型水利工程一般多为政府投资,其具有公益属性和公共属性的特点,且小型水利工程多为农田水利工程。因此,在其施工过程中会涉及到水利管理部门、土地管理部门以及本地农户等多方面的约束和限制,决定了其不可预见事件的发生。在充分开了小型水利工程自身特点的基础上,结合其他种类建筑工程不可预见费的内容,将其主要的影响因素分为三类:
第一,设计变更因素。在小型水利工程的施工过程中,由于占据农户耕地、材料的替换或者地基处理等原因造成的设计变更费用的增加。
第二,不可抗力因素。该方面因素主要来自于不可抗力风险,如出现自然灾害、极端天气等不可抗力事件而造成的损失或增加的费用。
第三,价格变化因素。小型水利工程虽然工程体量不大,但是从项目决策到工程完工可能最少需要一年以上的时间,在这段时间内,工程所需的材料、人工等价格可能会随着经济波动而发生变化,导致成本增加。
1.2 测算模型
为了有效建立小型水利工程不可预见费影响因素测算模型,本文以内蒙古乌鲁木齐为例,对2019—2021年已完工的小型水利工程进行统计和梳理,以供建立测算模型使用。
首先,在测算变更因素方面,采用spss软件,基于2019—2021年梳理的数据,共42个项目,对因为变更因素所提高的费用占小型水利工程总投资的百分比进行拟合分析,具体结果见表1。

表1 因设计变更增加费用占总投资百分比
根据表1结果,发现其与偏态分布拟合程度较高,为后续便于生产随机数,将其转换为正态分布,其特征参数μ=0.020,σ=0.0057。
其次,在不可抗力因素方面,通过对乌鲁木齐2019—2021年已完工小型水利工程相关数据进行分析,发现不可抗力事件的发生概率较低,仅由于“新冠疫情”原因增加了防疫费用。由于可用于分析的数据比较少,故将其设定为服从三角分布,影响系数设定见表2。

表2 乌鲁木齐各区域不可抗力因素对不可预见费影响系数
根据表2可以看出,乌鲁木齐不可抗力因素对不可预见费影响系数最可能值为0.15%。
最后,在价格变化因素方面,对于水利工程所需材料的价格变化来说,一般从项目决策、预算和施工,一般为一年,即2019年1月预算价格为基础,施工准备工作一般在2020年1月,此时则应以2020年1月的材料价格为基础。本文以一个季度为一个周期,选取2019—2021年3年的水利工程建设所需要的主要材料价格数据作为本次分析对象,具体见表3—4。

表3 2019—2021年工程主要材料价格及用量
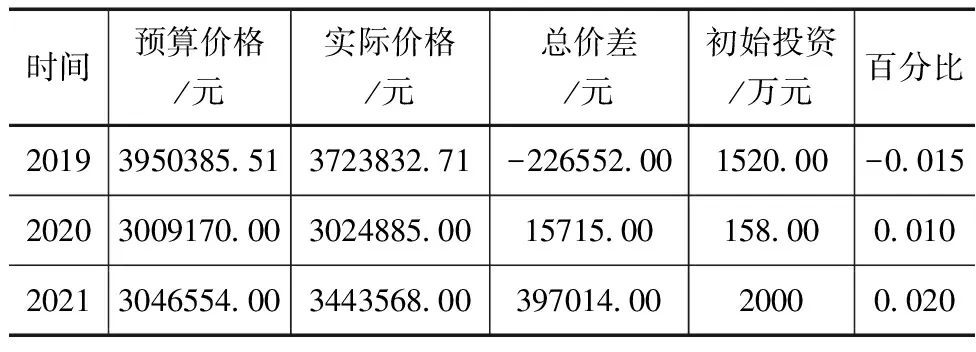
表4 2019—2021年主要材料总价情况
由于近3年数据并不充足,不足以充分反映市场价格的波动,因此,将其设定为服从三角分布,其影响系数见表5。

表5 价格变化对不可预见费影响系数
2 基于蒙特卡洛法的不可预见费测算
2.1 蒙特卡洛法
蒙特卡洛法也称为统计模拟方法或随机抽样法,是由美国数学家冯诺依曼和乌拉木在20世纪40年代首先提出的。
使用蒙特卡洛方法进行预测需要建立一个与预测对象相关的随机模型,该模型可以是离散型随机变量分布或者连续型随机变量分布。然后根据概率分布进行大量独立随机实验,取得随机变量的模拟值,然后使用数理统计方法求出样本数量特征值,也就是预测对象的近似解。其思路为:将影响不可预见费费率的因素视为自变量x1,x2,x3,…xn,且每个自变量对应的概率分布为f(x1),f(x2),f(x3),…f(xn)。将不可预见费费率视为因变量y,则有:
y=f(x1)+f(x2)+f(x3)+…f(xn)
同时,采用蒙特卡洛法进行模拟的步骤如下:
第一,对影响小型水利工程不可预见费因素的概率分布进行统计和分析;
第二,构建与小型水利工程不可预见费内容有关的数学模型;
第三,采用相关软件,如Matlab等进行模拟实验;
第四,对实验结果进行分析,确定小型水利工程不可预见费费率。
2.2 基于蒙特卡洛法的不可预见费测算
设计变更、不可抗力以及价格变化等因素之间相互独立又相互作用。因此,在确定不可预见费费率计算方式时,可以将三者系数进行叠加,即y=f(x1)+f(x2)+f(x3)。由此可得不可预见费计算公式:
y=Cf(x1)+Cf(x2)+Cf(x3)=Cy
式中,C—取费基数,即小型水利工程的初始投资。
根据上文计算结果,采用Matlab软件进行随机模拟,模拟次数为1000次。在模拟次数约300次之后,随机模拟的结果趋向于稳定,在约为0.05上下波动。同时,做出模拟结果的输出频数分布如图1所示。
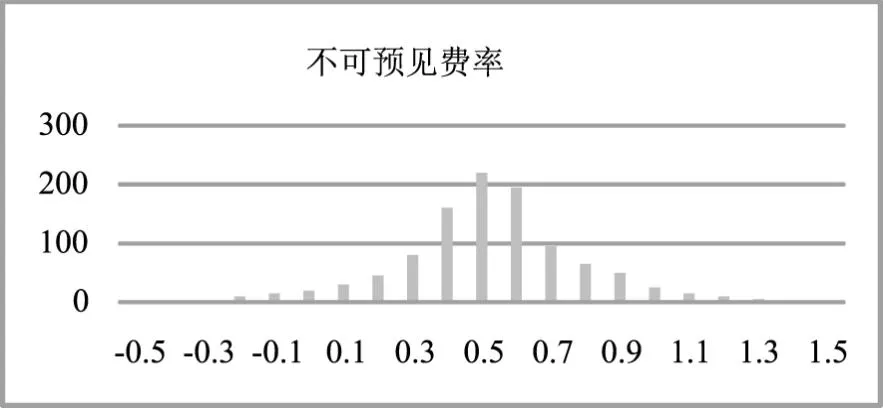
图1 不可预见费率模拟直方图
根据图1可以看出,不可预见费率呈现正态分布,对其进行拟合分析,服从μ=0.05,σ=0.024正态分布。因此,将乌鲁木齐市水利工程不可预见费费率的取费标准建议为工程初始投资的5%。
3 结语
本文考虑到当前的水利工程定额不适用小型水利工程不可预见费测算的基础上,分析了小型水利工程的特点以及不可预见费的取费标准。由此,在充分考虑特点的基础上,重点分析了水利工程不可预见费影响因素,提出了采用蒙特卡洛法测算小型水利工程不可预见费的思路,极大地弥补了小型水利工程不可预见费测算方面的空白,不仅提高了小型水利工程招投标总价控制效率,也大大促进了小型水利工程的可持续发展。同时,本文研究还存在不足之处,如本文的数据来源于乌鲁木齐市小型水利工程建设,对于其他地区是否适用还需要进一步的讨论。

