跨海大桥基础结构波流力计算方法

肖宇

（福建省交通规划设计院有限公司，福建 福州 350004）

0 引言

东吾洋跨海大桥位于福建省三沙湾内，为国高网宁德至上饶高速公路宁德霞浦至福安段项目的控制线工程。工程起于虾山鼻岛最西侧，跨越东吾洋，止于东安岛牛梁岗，工程位置示意如图1 所示。东吾洋跨海大桥所处海域水深较大，水深在30 m 以上的范围超过1.5 km，其中水深大于50 m 的范围约为0.9 km，最大水深为63 m。此外，较大的波高和流速也是东吾洋跨海大桥海域面临的难点，如100 a 一遇H1%达到4.43 m，100 a一遇设计流速达到2.2 m/s。水深、浪高、流急使得桥梁基础设计面临巨大挑战。如何合理确定基础结构形式及尺寸，以达到削减基础结构所受波流力的目的，对东吾洋跨海大桥工程至关重要，同时对今后跨海桥梁基础设计也具有普遍指导意义。

图1 工程位置示意图Fig.1 Project location diagram

目前国内外桥梁设计规范中并未给出跨海桥梁基础波流力的计算方法。实际应用中多参照港工规范进行估算或物理模型试验测定。根据结构特征尺寸与波长的相对大小，通常分为小尺度结构（D/L＜0.2，D 为结构特征尺寸，L 为波长）和大尺度结构（D/L≥0.2）。对于小尺度结构，任佐皋[1]、李玉成[2]分别对单桩结构的水动力系数进行研究，给出了单桩结构的速度力和惯性力系数。俞聿修等[3]通过试验研究分别给出了双桩并列和串列、三桩并列和串列时水动力系数随KC 数、相对桩距、桩数和桩位的变化关系。与小尺度结构不同，大尺度结构则必须考虑其对波浪场的影响。我国现行JTS 145—2015《港口与航道水文规范》[4]中对圆形墩和长宽比小于1.5 的矩形墩给出了计算方法。

跨海桥梁基础多采用桥墩-承台-桩基的形式，承台多设置于水位以下，且承台尺寸与桩基不同，沿水深属于变截面基础，而港工建筑物多采用桩基-面板的形式，码头面板设置于水位以上，沿水深属于等截面基础。故港工中的波流力计算方法并非完全适用于桥梁基础，还需专门针对桥墩-承台-桩基基础结构，建立波流力计算方法，并明确其计算精度。

1 跨海桥梁基础结构波流力计算模型

对于桥墩-承台-桩基基础结构，由于桥墩、承台和桩基三者尺寸差别较大，故需分别采用不同计算理论。

1.1 桥墩波流力

桥墩结构尺度一般较小，多属于小尺度结构，其波流力计算需基于Morison 方程。作用于底面以上高度z 处单位长度上的波流力f（z，t）为：

式中：fi和fd分别为柱体所受惯性力和速度力；γ为水的重度；CD和CM分别为速度力系数和惯性力系数；u 和u·分别为水质点轨道运动的速度和加速度；ωr为相对于水流的圆频率；ω 为水质点轨道运动圆频率；H 为波高；ɡ 为重力加速度；k 为波数；d 为水深；T 为平均波周期；U 为水流流速；t 为时间。

作用于桥墩上的总水平力F（t）和对桥墩底部的弯矩M（t）为：

式中：ZT为波面所能作用到的桥墩高度。

1.2 承台波流力

承台结构属于大尺度结构，其波浪力计算采用绕射理论。承台除圆形外，还较多地采用圆端形、方倒角形、哑铃形等复杂截面形状。对于任意复杂截面形状结构波浪力暂无解析解，需通过数值模拟计算。由于波浪-水流-结构物相互作用的复杂性，直接数值模拟承台结构的波流力是困难的，可通过分别计算承台波浪力和水流力，再利用两者耦合规律，得到承台所受的波流力。

1）任意复杂截面形状承台波浪力计算模型

扰动后的波动场内任一点的总速度势Φ 可表示为[5]：

式中：（x，y，z）为计算点坐标；i 为虚数单位；e 为自然常数；入射波速度势φI（x，y，z）满足Laplace方程、自由表面条件和底部条件，可表示为：

绕射波速度势φS（x，y，z）采用三维源汇分布法求解[6]，波动场中任一点q（x，y，z）所受到的扰动势是由结构物湿表面S（x，y，z）=0 上布置的点源M（ξ，η，ζ）引起的，若M 点的源强度为f（ξ，η，ζ）且在结构物表面上的分布是连续的，则在波动场中某一点q（x，y，z）的绕射势φS（x，y，z）可认为是由结构物表面上所有点源对q（x，y，z）点所引起的源势之和，即：

式中：（ξ，η，ζ）为变化点的坐标；f（ξ，η，ζ）为结构物表面上的源强度分布函数；G（x，y，z；ξ，η，ζ）为Green 函数。由式（10）可知，求解出波动场中任一点的绕射势，就必须求解出Green 函数G（x，y，z；ξ，η，ζ）和未知的源强度分布函数f（ξ，η，ζ）。

Wehausen 和Laitance（1960）给出了满足上述条件的Green 函数的级数形式[7]：

式中：ν=ω2/ɡ=ktanh kd；r 为计算点q（x，y，z）至源点M（ξ，η，ζ）的距离，r=[（x-ξ）2+（y-η）2+（z-ζ）2]1/2；J0（kr）和Y0（kr）分别为零阶第一类和第二类Bessel函数；K0（μmr）为零阶第二类修正Bessel 函数；μm为方程μmtan μmd+ν=0 的正实数根。

源强函数f（ξ，η，ζ）通过结构物表面S 上的流体运动边界条件确定：

式中：n 为结构物表面S 上某点的单位外法向矢量；nx、ny、nz分别为x、y、z 方向的分量。当求得结构物表面上的入射势φI（x，y，z）和绕射势φS（x，y，z）后，作用在结构上的波压力p（x，y，z，t），可由Bernoulli 方程计算：

对结构物湿表面波压力积分得到作用在结构上的水平波浪力和力矩：

2）承台波浪力与水流力耦合规律研究

上述模型可实现对任意复杂截面形状大尺度结构波浪力计算，但实际中往往还存在水流的影响，故还需考虑大尺度承台结构所受的水流力。关于承台波浪力与水流力耦合规律，试验研究表明[7-9]波流共同作用下的波流力值约为波浪力和水流力之和的1.04 倍。需要说明的是，此处波流力并非为波浪力与水流力的简单叠加，波浪力务必采用波流共同作用下的波长值进行计算或试验。

1.3 桩基波流力

桩基通常认为由小尺度单桩组成的桩群。桩基波流力计算需以Morison 方程为基础，并考虑群桩效应和相位影响。作用于底面以上高度z 处单位长度上的群桩波流力fN（z，t）为：

式中：Kj为第j 根桩的群桩系数；N 为群桩中桩柱的根数。

同一时刻，不同桩柱处水质点的速度uj（z，t）和（z，t）加速度为：

式中：（xj，yj）为第j 根桩的位置坐标；θ 为波浪作用的方向，定义为与坐标轴x 的夹角。

系数CD和CM可根据求得的KC 数按《港口与航道水文规范》[4]的规定取值。

作用于群桩上的总水平力和对水底总弯矩为：

式中：ZP为波面所能作用到的桩基高度，若桩基淹没，则为桩基在床面以上的高度。

至此，本文建立了适用于桥墩、承台和桩基的波流力计算模型。该模型不仅可对圆形承台，还可对矩形、哑铃形、圆端形等任意复杂截面形状承台波流力进行高效计算。需要说明的是，由于本模型建立基于势流理论，故尚不适用于破碎波对基础结构冲击力的计算。

2 计算模型的验证

为验证上述计算模型的准确性，在南京水利科学研究院波浪港池中开展了物理模型试验研究。试验桥墩基础如图2 和图3 所示（图中尺寸单位为m，高程基准面为1985 国家高程基准面，海床面高程为-61.9 m）。试验均遵照JTS/T 231—2021《水运工程模拟试验技术规范》[10]相关规定，采用正态模型，按照Froude 数相似律设计。模型几何比尺均取为58。

图2 试验桥梁基础构造图（主墩基础）Fig.2 Test bridge foundation structure diagram（Main pier foundation）

图3 试验桥梁基础构造图（引桥墩基础）Fig.3 Test bridge foundation structure diagram（Approach pier foundation）

试验以不规则波为主，不规则波的波谱采用Jonswap 谱，模型中的波高、波周期等物理量按重力相似准则确定。模型中的流速也按重力相似准则确定。试验波浪和水流要素如表1 所示。

表1 试验波浪和水流要素Table 1 Test wave and current elements

试验时先在波浪港池中模拟设计水流，再在有水流的基础上模拟给定的波要素，然后安放桥梁基础模型，进行波浪水流力试验。

采用上述方法的桥墩和承台、群桩受波流力计算值与试验值的对比如表2 所示。由表2 可知，本文计算值与试验值吻合较好，平均误差为5.0%，最大误差在10%以内，且计算值略大于试验，即计算结果略偏安全。因此，本文建立的跨海桥梁基础波流力计算方法可应用于同类跨海桥梁基础波流力计算。

表2 波流力计算值与试验值对比Table 2 Comparison between the calculated and experimental values of the wave current force

3 东吾洋跨海大桥基础波流力计算

3.1 基础结构方案

选择何种形式的基础方案，以达到减小桥梁基础所受波流力的目的是东吾洋跨海大桥工程的重要研究内容之一。

为此提出了不同的设计方案，见图4—图7（图中尺寸单位为m，高程基准面为1985 国家高程基准面，海床面高程为-62.5 m）。4 种设计方案的差别主要在于承台截面形状和桩基布置形式。方案1 为八边形承台，桩基采用错位行列布置；方案2 为圆形承台，桩基沿圆周布置；方案3 为矩形圆倒角承台，桩基均为规则行列布置；方案4 为菱形圆端承台，桩基采用行列布置，并在两圆端各补充布置1 根桩。

图4 东吾洋跨海大桥主墩基础比选方案1Fig.4 Dongwuyang cross-sea bridge main pier foundation comparison scheme 1

图5 东吾洋跨海大桥主墩基础比选方案2Fig.5 Dongwuyang cross-sea bridge main pier foundation comparison scheme 2

图6 东吾洋跨海大桥主墩基础比选方案3Fig.6 Dongwuyang cross-sea bridge main pier foundation comparison scheme 3

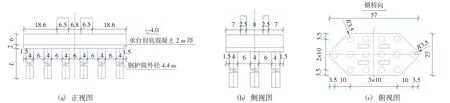
图7 东吾洋跨海大桥主墩基础比选方案4Fig.7 Dongwuyang cross-sea bridge main pier foundation comparison scheme 4

3.2 基础结构波流力对比分析

采用本文建立的波流力计算方法，对不同方案基础结构所受波流力进行计算，计算结果如表3 所示。由表3 可知，不同的结构设计方案所受的波流力存在一定差别。从桥墩和承台受力来看，横桥向以方案2 所受的波流力最大，方案4 所受的波流力最小；顺桥向以方案3 所受的波浪力最大，方案1 所受的波浪力最小。

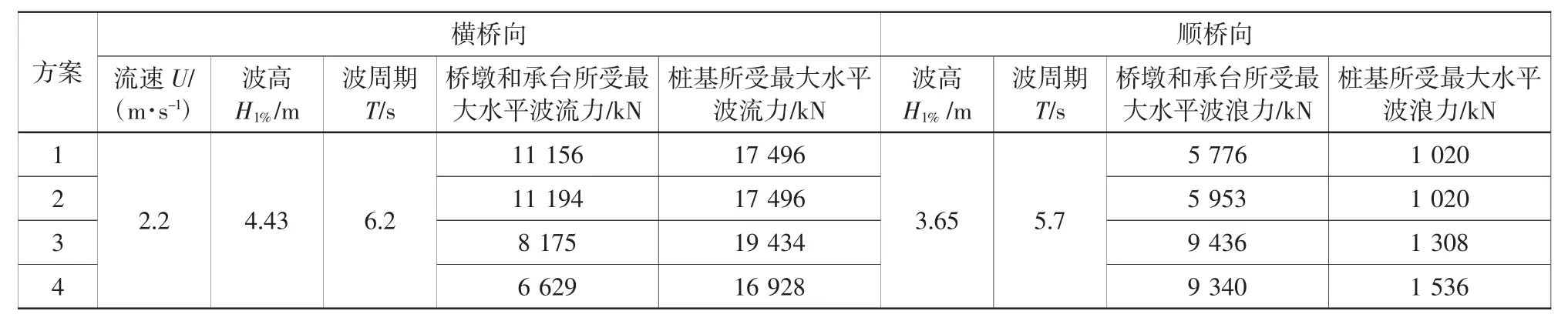
表3 东吾洋跨海大桥主墩基础结构不同方案波流力对比Table 3 Comparison of wave current forces for different schemes of the main pier foundation structure of Dongwuyang cross-sea bridge

对于桥墩和承台所受最大水平波流力，尽管方案2 的迎流面宽度（41 m）大于方案1（37 m），但方案1 和方案2 的受力基本一致。这主要是由于方案2 为圆形结构，其形状阻力系数小于八边形。对比方案4 和方案3，横桥向方案4 的宽度较方案3 仅减小1.3%，但方案4 的横桥向受力较方案3 减小达19%左右，顺桥向以此类推，从减小承台结构受力考虑，宜采用圆形或菱形截面结构形式。

从桩基受力来看，不同方案的桩基横桥向受力均明显大于顺桥向。这主要是由于桥轴线走向与设计水流流向基本垂直，桥梁基础横桥向受波浪和水流共同作用，而顺桥向仅为波浪作用。对比不同方案桩基横桥向受力可知，方案3 桩基受力最大，方案4 桩基受力最小，两者相差13%左右，这主要是桩基数量和布置形式不同所致。方案3 桩基数量为18 根，方案4 桩基数量为14 根。因此从减小桩基受力方面考虑，应尽量减少桩基的数量，增大桩基间距，但这将导致桩基直径和承台尺寸的增加，进而影响基础结构受力。因此还需结合承台受力，确定最佳的桩基布置方案。

综合以上不同方案基础波浪（流）力的对比分析，从减小桥梁基础所受波流力考虑，主墩结构宜采用方案4。

4 结语

桥墩-承台-桩基是跨海桥梁、海上风电基础广泛采用的结构形式之一。目前国内外桥梁设计规范中并未给出成熟可靠的计算方法。本文基于Morison 方程、绕射理论以及波浪力与水流力耦合规律，建立了桥墩、承台、桩基波流力的成熟高效计算模型，并经验证后将其应用于东吾洋跨海大桥工程。主要研究结论如下：

1）桥墩-承台-桩基基础结构由于桥墩、承台和桩基三者尺寸差别较大，需分别采用不同计算理论。桥墩一般属于小尺度结构，波流力计算可基于Morison 方程，承台结构多属于大尺度结构需采用绕射理论。桩基为群桩结构，需考虑桩基的群桩效应和相位效应。

2）经与物理模型试验值验证，本文模型计算值与试验值的误差在10%以内，且计算值略偏安全。由于避免了繁杂的流场计算，使得本文模型计算效率远高于CFD 方法，但本文模型尚不适用于破碎波对基础结构冲击力的计算。

3）本文模型应用于东吾洋跨海大桥主墩基础方案比选，得到了基础结构受力较小的优选方案。本文建立的计算模型可推广应用于同类跨海桥梁、海上风电基础设计中。