船舶操纵性约束模测量系统设计与分析
王 飞,马雪泉,谢凤伟,吴永顺
(1.上海交通大学 船建学院,上海 200240;2.上海船舶运输科学研究所有限公司,上海 200135;3.中国船舶及海洋工程设计研究院,上海 200011)
0 引言
船舶操纵性是船舶一种最为基本的航海性能,随着现代新型船舶的出现、航运业的发展及海上航行密度的提高,新建船舶必须满足国际海事组织“IMO船舶操纵性标准”中的要求,为此需要在设计阶段展开研究,准确预报实船的操纵性能。迄今通过建立运动方程,展开约束模实验,确定水动力导数,来进行数值仿真计算,是预报船舶操纵性基本的、可靠的研究手段[1-3]。
约束模实验通常采用平面运动机构(PMM,planar motion mechanism)在水池或水槽中展开,其可以进行斜拖、横荡、艏摇及组合等诸多约束模实验。约束模实验的基本原理在理论上很早就已经提出,但作为实际工程应用问题,实现这些原理的技术,鲜有公开文献发表,特别是精确的、可靠的实验测量及数据分析处理技术[3-4]。为此本文以此为背景,利用已有的平面运动机构设备,展开测量与数据分析技术研究。设计测量软硬件方案,推导数据处理与分析算法,编写程序,以期实现数据在线测量、分析与处理。为保证系统的自主性,本文不借助Matlab、LabView等外部工具,基本及主要功能内部自主实现。
1 测量分析系统方案设计
约束模实验通常利用平面运动机构在拖曳水池或水槽中展开,其中平面运动机构固定于拖车框架上,一般独立操控;船模通过测力天平经过可升降的无摩擦机构连接于平面运动机构上,船模自由升沉纵倾。实验时平面运动机构带动船模向前运动,流体作用在船模上的作用力最终以模型约束力的形式作用在测量天平上,这些作用力输入测量分析系统完成实验数据采集与处理分析。
对应的测量及数据分析程序,为保证效率与便捷性,具有以下基本功能:
1)作用力及传感器等信号在线采集显示;
2)数据采集兼具手动开始及触发开始;
3)平面运动机构运动姿态监测;
4)舵角螺旋桨转速等外设的在线操控;
5)较完善的数据后处理功能,包括水动力导数的在线计算及图表绘制;
6)良好的扩展性,以兼容不同的仪器设备。
相对于其它常规测量系统,本文系统需要在有较强电磁干扰环境下,精确解决横荡艏摇等动态约束模实验的零相位起始整周期测量问题;确保测量在运动周期的零相位开始,并精确测量整数个周期。
根据这些目的,本文在已有的平面运动机构的基础上,组建了如图1所示的实验测量分析系统。为了确定横荡、艏摇等动态约束模实验的零相位,本文在平面运动机构上额外设置了开始触发装置(光电开关),并将其接至数据采集系统的触发端口上。
整个测量系统设备主要包括以下几部分:
1)平面运动机构:本实验室已有设备,运动幅度达1.0 m,为独立操控。
2)数据采集:康泰克多功能PCI数据采集卡1套,16位精度,采集的数据包括测力天平作用力、平面运动机构姿态、触发信号等。
3)运动控制:研华4路步进/伺服电机控制卡1套,用于控制舵角及螺旋桨转速。
4)光电开关:采用红外对射光电开关,TTL数字信号输出以降低干扰;数量共3个,其一安装于平面运动机构中心,作为触发信号使用;另两个安装于两侧,用于左右限位报警。
5)辅助机构:舵角控制采用步进电机,螺旋桨转速控制采用伺服电机,共4个电机,分别对应左舵右舵和左桨右桨;线位移传感器及角位移传感器各一个,用于测量平面运动机构的横向位移和艏向角度。
1.1 数据采集方案
数据采集系统由16位32通道康泰克PCI数据采集卡组成,其具有硬件触发启动及触发停止功能,用于采集测力天平的输出电压信号,同时采集角位移及线位移传感器等信号,配合测量分析程序完成数据的在线采集、处理、显示及存盘等功能。
1.2 零相位整周期测量方案
对于横荡、艏摇等动态约束模实验,其测量起始点需要从正弦函数y=sin(ωt)的相位零点开始,也即一个运动周期的起始时刻开始数据采集。由于PMM从开始运动到稳定自身有一个启动过程,前面2、3个周期是过渡的,后续周期才是稳定可用的。精准控制(计时控制精度为毫秒级)在一个周期的起始时刻开始数据采集,手工无法实现,只能采用硬件触发的方式开启。
本文采用以数字信号输出的红外光电对射开关,以触发方式来启动数据采集。其中光电开关位于PMM中心位置,其信号接至数据采集卡的触发端口,当其光线没被阻挡时输出低电平,而当PMM由左侧运动至该位置时光线被其上的一微小挡板阻断,光电开关输出5 V高电平,数据采集卡自动开启数据采集。同时为数据处理检测之用,该触发信号一并接入采集卡的采集通道。
在编写测量分析系统程序时,需将采集模式设置为触发启动模式。程序中,点击开始后首先使用采集卡触发函数AioSetAiStartTrigger 设置信号上升沿为启动模式,然后使用函数AioResetAiMemory和AioStartAi启动数据采集,此时程序并未开始采集数据,只是监测触发信号,收到触发信号后才真正开始采集。待采集3、4个周期后,使用AioStopAi停止采集。
数据采集完成要停止时,因傅里叶分析的要求,采样时长必须精确地为运动周期的整数倍,手工无法实现,硬件触发停止也有诸多不便。本文采用软件方法实现:数据采集完成后,对光电开关信号进行处理,检测其上升沿信号,以最后一个偶数次上升沿作为停止时刻,此时刻之前的数据为有效数据,进行在线处理,此后的数据直接忽略。
1.3 平面运动机构姿态监测
监测系统是为了实时记录整个系统的运动姿态,主要作参考之用,为后期数据处理分析提供运动姿态数据。该部分由角位移传感器、线位移传感器和数据采集卡组成。其中角位移传感器通过塑料绝缘件连接于平面运动机构的艏摇轴上,线位移传感器通过塑料绝缘件连接于平面运动机构的横荡机构上,这两个传感器信号全部接入数据采集卡由采集系统进行后台采集。
1.4 桨舵的控制
本文采用研华四路运动控制卡来程控船模的舵角和螺旋桨转速,舵角采用步进电机进行控制,螺旋桨转速采用伺服电机进行控制,以CW/CCW脉冲方式运行[5]。其中第1,2路用于控制左、右舵的舵角,以点位模式运行;第3,4路用于控制左、右桨的转速,以速度模式运行。
测量分析程序中,舵角的控制采用如下方式实现:使用函数Acm_SetF64Property设置转舵的起始速度(PAR_AxVelLow)、运行速度(PAR_AxVelHigh),加速度(PAR_AxAcc)、减速度(PAR_AxDec)和TS过渡曲线(PAR_AxJerk),为减小转舵扰动,运行速度应为小量,可设置为1~3°/s;然后使用Acm_AxMoveAbs或Acm_AxChangePos驱动电机转动舵角。螺旋桨转速的控制实现方法类似,首先使用函数Acm_SetF64Property设置起始速度、运行速度、加速度、减速度及过渡曲线,其中运行速度为螺旋桨的目标转速,然后使用函数Acm_AxMoveVel或Acm_AxChangeVel转动螺旋桨;停止则使用Acm_AxStopDecEx函数。
2 约束模方程及数据处理方法
本文采用如下三自由度船舶操纵性运动控制方程:
(1)
式中,m,Izz分别为船舶的质量及转动惯量;u,v,r分别为船舶纵向、横向速度及转首角速度,其上面的点表示对时间求导,即运动加速度;X,Y,N分别为船舶纵向、横向及艏向的约束力;而各个带下标的X,Y,N分别为对应的水动力导数,如Xuu为纵向水动力关于u的二阶导数,Yv为横向水动力关于v的一阶导数,限于篇幅其余导数意义可参考文献[3],而对应的无因次导数在其后加撇号(’)表示。本文限于篇幅仅简要给出斜拖、横荡和艏摇3种约束模实验的方程及数据分析处理方法。
2.1 斜拖数据处理
斜拖实验为稳态实验,船模运动速度为U,漂角为β,其余运动参数为零,将其代入式(1)得斜拖约束模方程:
(2)
式中,u=Ucos(β),v= -Usin(β),Xuu本文用零漂角的值直接进行计算;对于该斜拖方程,在测量完不同漂角的约束力后,将其转换为基本的y=a+bx线性函数,应用最小二乘拟合算法[6-8]计算各水动力导数,转换公式为:
(3)
根据操纵性研究国际惯例,需将有因次导数转换为无因次形式,本文采用C=F/(0.5ρL2U2)的形式进行无因次化。
2.2 横荡数据处理
横荡为动态实验,一般只用于分析惯性类水动力导数。船模速度为U,平面运动机构横向作y=a·sin(ωt)运动,运动幅值为a,角频率为ω,将其求导确定横向速度及加速度并代入式(1),得横荡约束模方程:
Yvva2ω2|cos(ωt)|cos(ωt)
Nvva2ω2|cos(ωt)|cos(ωt)
(4)
根据傅里叶分析的原理[6-8],对应水动力导数为:
(5)
式中,Fourier_sin1(Y)表示计算作用力Y的傅里叶sin项1阶次系数,其余类似。
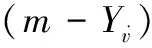
(6)
2.3 艏摇数据处理
艏摇实验为动态实验,船模速度为U,平面运动机构横向作y=a·sin(ωt)运动,艏向作Ψ=arctan(aω/Ucos(ωt))运动,漂角β≡0,将这些运动参数代入式(1),并进行傅里叶分析,可得到对应的水动力导数的艏摇运动方程:
Fourier_cos0{X-XuuU2[1+k2cos2(ωt)]}
(7)
Fourier_sin1(Y-ma2ω2sin(ωt)cos(ψ))
(8)
(9)
Fourier_sin1(N)
(10)
式中,k=aω/U,ψ为艏向角,以上各水动力导数本文建议用合速度周期均值Um进行无因次化,其均值近似为:
(11)
为保证精度,特别是高阶项导数的精度,需要改变幅值a进行(≥5)个工况的测量。在所有工况测量完成后,根据式(7)~(10)应用最小二乘拟合算法计算各个水动力导数。其最小二乘转换公式为同式(3)、(6)类似,限于篇幅不再给出。
3 测量分析程序
在以上工作的基础上,本文编写了测量及数据处理分析程序[8-12]。该程序全部采用C语言编写,可运行于Win2000~Win10系统,主要功能内部自主实现,程序界面如图2所示。为兼顾扩展性,程序分为两大部分,即专用的主控程序部分和通用的辅控程序部分(舵角控制、转速控制、运动指示等),辅控程序由主控程序联机在线自动操控,也可手控运行。
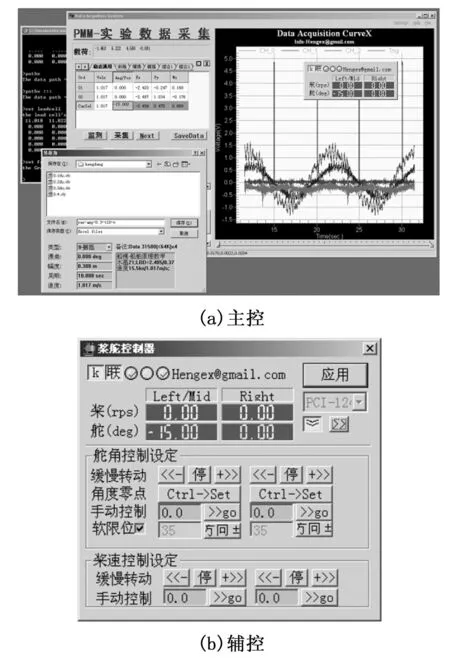
图2 船舶约束模测量分析程序
程序中已内置配套传感器的系数,可以直接使用,也可重新标定。数据记录方面,采用Excel以多页表形式存储所有设置性、结果性数据,而原始测量数据因数量巨大则以二进制文件另行保存。
在进行测量前,首先根据实验类型将程序数据处理方式调至斜拖、横荡或艏摇等界面;并根据需要进行传感器系数标定及零点采集。
测量时,程序在线完成数据的采集与结果的计算处理,并记录存盘。当每组约束模所有工况完成后,通过程序菜单或字符控制台模式,进入水动力导数的在线分析处理界面,在线计算各水动力导数,检验导数拟合曲线及原始测点曲线。如发现拟合曲线和测点曲线偏差较大,则表明数据可能存在较大误差,可直接再次进行重新测量即可,而不用等后期发现问题后再来重测。
3.1 传感器标定
作为一项基本功能,程序已内置传感器的标定功能。标定时将程序数据处理调至标定界面,根据需要进行测力传感器、线位移传感器及角位移传感器的标定。
本文采用两点线性方法标定:
y=k(u-u0)
(12)
其中:y为传感器对应的物理量,u为传感器输出电压,u0为电压零点。标定流程如图3所示(以线位移传感器为例)。
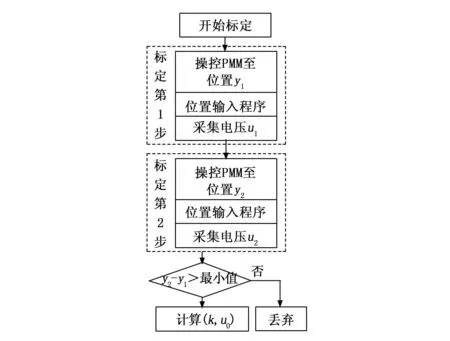
图3 传感器系数标定流程
其中,需保证精度两步中传感器的物理量差(y2-y1)足够大,否则忽略该传感器的标定,其仍采用原先值。
标定结束后,程序自动记录这些传感器系数和电压零点。因传感器的零点在不同情况下一般会出现一些变化,故程序中电压零点可以单独另行设置。
3.2 数据在线采集与处理
因作者通常使用的数据采样速率均较高(≥1 000 Hz),程序中不能采用软件轮询的方式进行数据采集与处理。本文采用硬件缓存采集方式进行,简要方案或步骤如下。
1)进行采集设置:设置数据采样率,采样通道,设置后台FIFO缓存采集方式。
2)设置后台回调函数,此函数负责数据在线采集与处理,并绘制显示实时曲线;为防止程序堵塞,该回调函数仅进行最基本的数据处理与显示。
3)数据采集完成后,停止当前工况的采集,对测量数据进行初步处理。对于斜拖,因其是稳态工况,直接计算各约束力(X,Y,N)的均值并作记录;对于横荡艏摇等动态工况,首先对触发信号进行处理以确定实际运动周期,然后采用傅里叶分析,计算约束力的各个阶次的傅里叶系数,本文中计算零阶至三阶傅里叶系数,并作记录。
待每组约束模所有工况完成后,进行水动力导数的在线处理;采用式(2)、(3)对斜拖中间结果进行最小二乘拟合确定斜拖导数,采用式(5)~(10)对横荡艏摇结果进行最小二乘拟合确定其各自导数。
3.3 主控辅控程序的互联
在测量过程中,为提高效率,辅控程序自动接受并执行主控程序指令,无需手工介入。联机时主控程序自动下发运动指令并监测运动状态,辅控程序则接收指令驱动机构运动,并向主控返回当前状态。在程序中,它们之间采用以下方式建立通讯互联:
1)主控程序使用函数FindWindow 搜寻辅控程序。
2)主控程序使用函数SendMessage 向辅控程序发送握手消息,辅控程序应答,建立通讯。
3)主控、辅控程序使用函数PostMessage 互相通讯互联。
4 实验测量及分析
在测量分析系统开发完成后,本文进行了简单的实际测试,以验证以上各项工作。测量对象如图4所示,船模长度为2.485 m,船模质量m=56.5 kg(m′=0.071 9);实验水温21 ℃,流体密度997.996 kg/m3;船模运动速度根据实船目标航速采用傅汝德相似原理进行确定,为1.017 m/s;斜拖时,漂角工况共11个,分别为β=-30,-20,-15,-10,-5,0,5,10,15,20,30°;横荡及艏摇时,PMM运动设定周期10 s,运动幅度a=0.1,0.2,0.3,0.4,0.5 m。下面给出具体的测量结果,并作简要分析。

图4 实验测量船模
4.1 测量过程及结果分析
斜拖实验为稳态运动测量,漂角依次由-30°调整至+30°,每工况采样时间≥20 s,取其时间均值作为最终结果,表 1给出了斜拖不同漂角时的模型约束力。
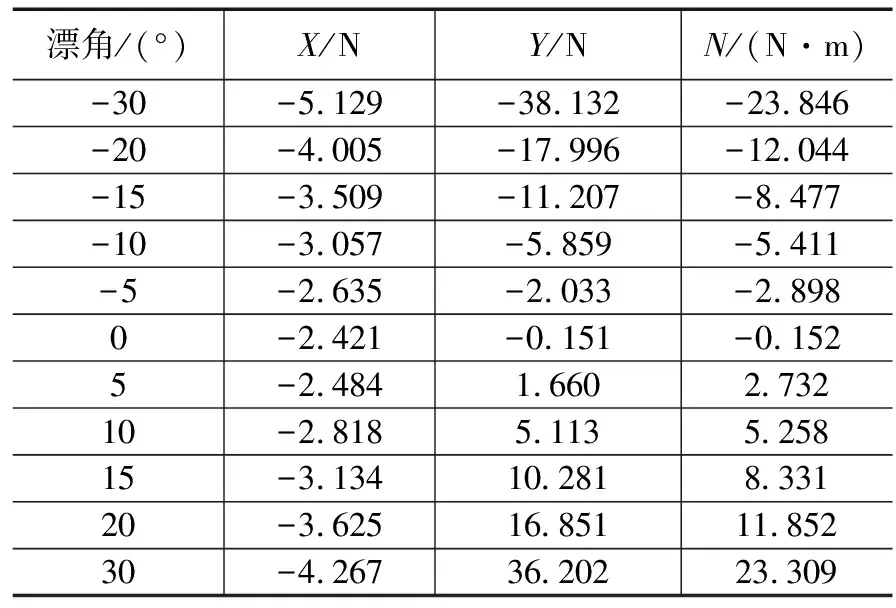
表1 斜拖约束力测量结果
因船体左右对称,理论上,约束力X关于漂角偶对称,约束力Y和N关于漂角奇对称。但测量中因模型加工误差、安装偏差、测力天平误差等各种因素影响,这3个约束力关于漂角并不完全对称性。测量结果显示,约束力X对称性稍差,其原因为X数值较小,一个小的误差就会产生较大的影响;而约束力Y和N因其数值较大,误差影响较小,其对称性比较理想。整体而言,斜拖测量结果是比较理想的。
横荡和艏摇实验为动态运动测量,实验时首先启动平面运动机构进行横荡艏摇运动,待平面运动机构运动2,3个周期到达稳定后,然后在程序中点击开始采集,以触发启动方式开启数据采集,随后当平面运动机构运动到中间,也即相位零点时,程序根据光电开关触发信号,自动开启数据采集。
图5和图6给出了部分横荡和艏摇测量结果,图中包括了模型约束力(X,Y,N),触发信号(Trig)及平面运动机构横向位移y和艏向角Ψ的历时曲线,其中触发信号单位为电压V,横向位移单位为m,艏向角单位为rad。
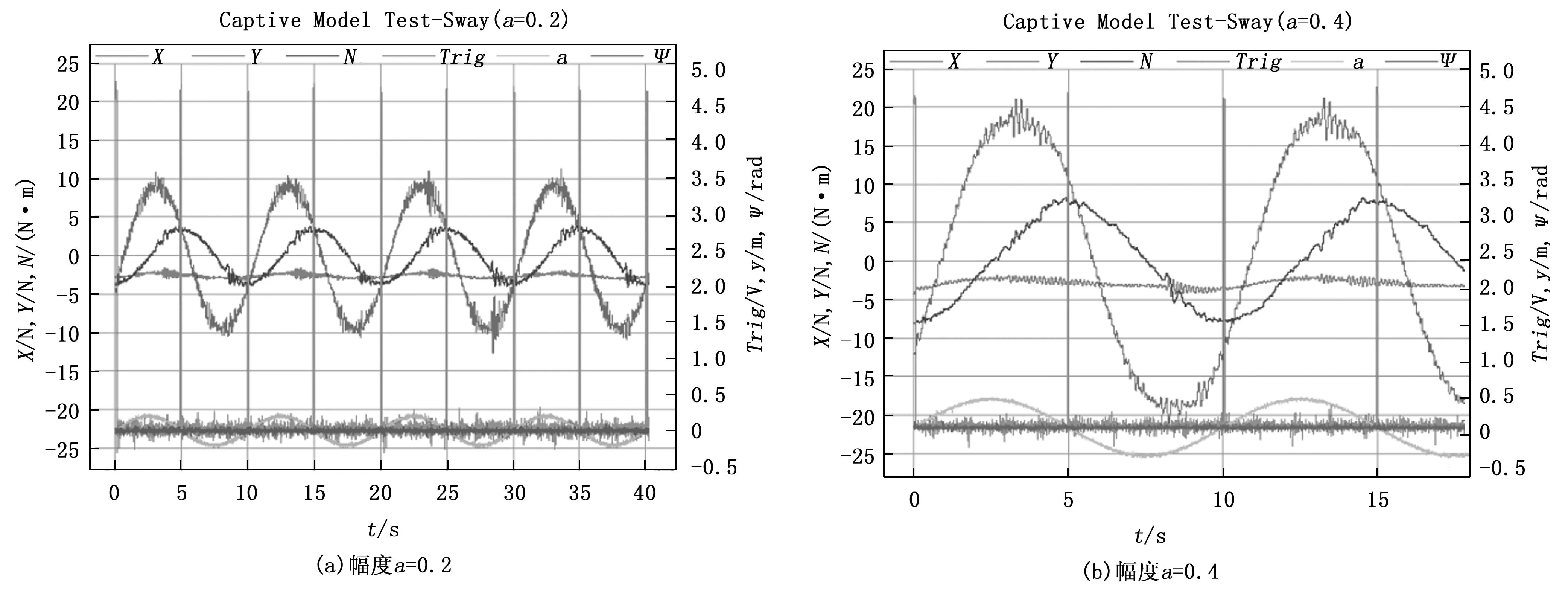
图5 横荡测量原始数据

图6 艏摇测量原始数据
结果显示:数据采集开始时刻正好对应触发信号前面的上升沿,无延后或超前;触发信号约5秒一次,分别对应0°和180°相位,高电平时间极短,仅几十个毫秒,对应光电开关被挡板阻挡的时间;约束力(X,Y,N)横荡时表现为较理想三角函数曲线,而艏摇时则表现为变形的三角函数曲线,其原因为高阶项作用力的影响较大以致曲线变形;而平面运动机构横向位移曲线y,为理想的正弦函数曲线,零时刻位移y=0,运动幅值和设定值一致,可以认为平面机构的运动,测量系统姿态监测结果同预期结果一致;图6显示艏摇时,艏向角曲线同位移曲线相差90°相位,角度幅值和设定值一致,符合预期结果。
根据以上测量结果可以认为,本文开发的测量系统及编写的测量程序在稳态测量、动态测量、触发采集、运动监测等方面,测量结果和预期结果一致,满足约束模实验的各项要求。
4.2 数据处理结果
根据以上测量结果,进行数据处理分析,以确定对应的水动力导数。根据式(3)对斜拖数据进行在线数据处理,结果如图7所示,其中的点线为测量数据,连续曲线为导数的拟合结果;可见X作用力拟合有些偏差,其导数精度可能有些偏低,而Y,N作用力拟合结果很好,说明Y,N导数的精度较高。
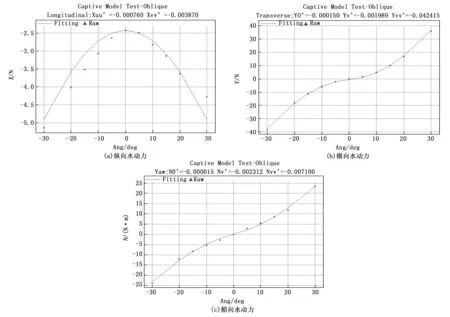
图7 斜拖水动力导数处理结果
根据式(5)、(6)对横荡数据进行在线数据处理,结果如图8所示。

图8 横荡水动力导数处理结果
根据式(7)~(10)对艏摇数据进行在线数据处理,结果如图9所示。
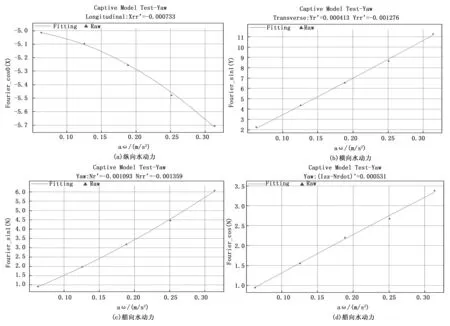
图9 艏摇水动力导数处理结果
根据以上处理结果可以看出,测量结果同水动力导数的拟合曲线,除个别点外均符合得较好;说明了本文测量系统及数据分析处理方法的正确性与可靠性。
综合以上各图表,船舶的水动力导数如表2所示。
4.3 触发信号及运动周期分析
横荡及艏摇测量结果曲线显示,数据采集起始时刻位于触发信号(Trig)的上升沿起点及止点之间,但上升沿时间极短,不足1~2 ms,触发信号(光电开关信号)上升沿在采集系统中不一定会记录下来。
故在测量完成后确定实际运动周期时,需将光电开关信号起始的1~2 s数据跳过,检测其后第偶数次(偶数次对应360°相位)上升沿信号作为实际周期;同时结果显示触发信号中有一定的噪声,为剔除噪声干扰本文建议以触发信号上升幅度大于50%高电平作为判断基准,以确保系统的可靠性。
同时对测量结果分析发现,系统存在横荡艏摇运动实际周期同设定值不一致问题。实测结果图5及图6显示第4周期的上升沿对应约40.026 s,对应周期为10.006 5 s,同设定周期10 s相比偏差约为0.7‰。其原因可能为PMM和测量系统的计时基准有些差异;为了保证数据处理精度,本文建议使用实测周期进行数据处理。
4.4 噪音与振动问题
测量结果显示,信号噪声及振动一直比较大,特别是靠近PMM艏摇电机的地方,而离其较远的线位移传感器噪声则相对小许多,这些噪声可能会对结果造成一定的负面影响。为了减小噪声干扰[13-20],可能要增设零相移滤波器对信号进行滤波处理,这些待以后改进。
5 结束语
本文的工作解决了船舶操纵性约束模实验测量中相关应用技术问题,基于平面运动机构设计给出了较为完整的约束模实验测量分析系统,并成功应用于实际工程实验。文中采用数据采集卡、运动控制卡及各类传感器等组建了约束模测量系统,并采用光电开关来精准实现横荡艏摇实验数据采集的触发启动,解决了动态实验中的零相位整周期测量问题;推导给出了约束模各水动力导数的数据处理分析方法,采用C语言开发了较为完善的约束模实验测量及数据处理分析程序,可实现约束模实验的在线处理与分析,完成各水动力导数的辨识。通过实际测量,验证了本文所开发的系统。本文研究的展开,对于类似实验运动机构或技术的开发可提供有益参考。

