Memory effect in time fractional Schrödinger equation
Chuanjin Zu(祖传金) and Xiangyang Yu(余向阳)
School of Physics,State Key Laboratory of Optoelectronic Materials and Technologies,Sun Yat-Sen University,Guangzhou 510275,China
Keywords: time fractional Schrödinger equation,memory effect,non-Markovian environment
1.Introduction
In classical physics, time has been traditionally treated as isotropic,and space as homogeneous.Researchers have extensively employed conventional mathematical methodologies to develop quantum systems, yielding remarkable achievements.However, with the deepening of research, a growing realization of the fractal characteristics of space and the non-Markovian behavior of statistical phenomena has emerged.[1–6]This revelation highlights that many physical processes exhibit nonconservative traits, rendering the sole reliance on integer-order calculus inadequate for comprehensive description.Fractional calculus, which has a long history as integer calculus, has become an important tool for the description of memory and hereditary properties of various materials and processes.[7–11]In practical computations,temporal fractional derivative operators are introduced to effectively account for memory effects inherent in physical systems.Simultaneously, to aptly capture the fractal essence of space, spatial fractional derivative operators come into play.This combined employment of fractional derivative operators for both time and space enriches our ability to model and understand the intricate behaviors exhibited by various physical phenomena.[12,13]
The utilization of fractional calculus within the realm of quantum physics finds its origins in the pioneering contributions of Laskin.[14–16]Subsequent to these seminal works, the integration of fractional calculus into quantum theory has burgeoned into a swiftly expanding domain of study.Notably, the incorporation of concepts like the space fractional Schrödinger equation,[16]the time fractional Schrödinger equation (TFSE),[17]and the space–time fractional Schrödinger equation[18,19]has ushered in a phase of advancement in the realm of fractional quantum mechanics.Currently,the most of studies on fractional quantum mechanics focus on the fractional Schrödinger equation.[20–30]Over the last two decades,substantial strides have been achieved in both theoretical developments and experimental applications of the space fractional Schrödinger equation.Nonetheless, a consensus regarding the precise mathematical formulation of the time fractional Schrödinger equation has yet to be reached.The primary impediment lies in the fact that the proposed TFSE by Naber contradicts certain fundamental principles of physics,such as the Hermitization of the Hamiltonian and the conservation of probability law.[17,18]To address these limitations, researchers have embarked on a dual-track approach to elucidate this phenomenon, examining it through both mathematical and physical lenses.Within the realm of mathematics,some scholars posit that the divergent interpretations stem from variations in the definitions of fractional derivatives and the distinct treatment of the imaginary unit i.In Ref.[26],Zu constructed time fractional Schrödinger equation with a limit based fractional derivative.In physics, Narahari Achar reconstructed the TFSE using the Feynman path integral technique for a nonrelativistic particle.[31]Indeed, certain among the aforementioned investigations have overlooked a crucial aspect: the presence of memory effects within the framework of the time fractional Schrödinger equation.
The exploration of open quantum systems stands as one of the most formidable frontiers in the realm of quantum information science.[32,33]Depending on the approaches employed for handling environmental interactions, open quantum systems can be dichotomized into two categories:Markovian processes and non-Markovian processes.Among these, Markovian processes are the simplest case in the evolution of open quantum systems, and the system evolution can be described by a simple master equation.[34]Nevertheless, the dynamics of the system take on a heightened complexity upon the inclusion of memory effects originating from the environment.The pursuit of efficacious methodologies for scrutinizing system evolution amidst non-Markovian surroundings remains an emerging and vibrant realm of investigation.[35–39]In a notable instance, within Ref.[25], scholars delve into the time fractional evolution of both a single quantum state and entangled state, thereby introducing the ground-breaking consideration of impact of memory of TFSE on quantum states.The authors differentiate the memory depicted in TFSE from the influence of the external environment,positing that this memory is inherently distinct and unaffected by external factors.The findings reveal an intriguing facet: the memory effect characterized by TFSE displays instability, and its impact is not universally affirmative.This contrast to conventional memory within a non-Markovian environment underscores a significant departure.In non-Markovian processes, the memory originates from the feedback impact of the environment on the system and the memory effect consistently manifests in a positive manner.The more pronounced the memory effect, the more robust the system becomes against interference.This observation stimulates deeper contemplation: could the memory embedded within the time fractional Schrödinger equation also stem from environmental feedback? If so,would the outcomes diverge?
In this paper,we delve into the memory of the time fractional Schrödinger equation.Drawing inspiration from the dynamics of non-Markovian environment, we posit that the memory of the time fractional Schrödinger equation mirrors the environment’s feedback.Succinctly put, where memory exists, interference follows — a fundamental link between memory and interference.From this point of view, we verify the necessity of not performing fractional order operations on imaginary unit i and find that time fractional Schrödinger equation properly describes the evolution of quantum states in non-Markovian environments.Meanwhile, we also prove that it is meaningless to study the memory of time fractional Schrödinger equation for 1<α ≤2.Our work provides a new idea for the study of time fractional Schrödinger equation.Simultaneously,it also provides new tools for describing non-Markovian processes.
This paper is organized as follows.In Section 2,we give a brief description of time fractional Schrödinger equation and its memory.Then in Section 3,we verify the effect of memory on a quantum state.Finally, the discussions and conclusions are summarized in Section 4.
2.Time fractional Schro¨dinger equation and its memory
In terms of different treatments to the imaginary unit i,Naber constructed two types of TFSE,[17]which can be expressed as

where Γ(1-α) is the Gamma function andf′(τ) is the first order time derivative.The memory of TFSE is reflected in the order of fractional derivativeα.In order to further explain the root cause of its memory,we rewrite Eq.(3)as


3.The effect of memory on a quantum state
In this section, we study the effect of memory of TFSE on a single quantum state.Considering the particularity of the memory of time fractional Schrödinger equation,we need a free particle as the research object.Especially noteworthy is that while the physical model does not depict the systemenvironment interaction,the environment undeniably exerts a detrimental influence on the system.This influence predominantly manifests through the emergence of memory effects.Assuming that a two-level atom can be expressed as


As the time approaches infinity, the attenuation termFα[(-i)αwk,t] will tend to zero.[17]So, the total probability of the system is given by
It indicates that as time approaches infinity,the total probability varies with the parameterαand may be greater than 1.The greater the influence of memory,the greater the total probability.Lu thought that the increase of the number of particles can be viewed as the result that particles evolve from other states.[24]In particular, when the memory is maximum (e.g.,α →0),the number of particles becomes infinite and fills the whole space.This phenomenon is difficult to understand in non-Markovian environment.
In order to explain the evolution of quantum state in this situation in more detail,we plot Fig.1 to show the dependency between the real part ofc0and the parameterα.Whenα=1,it means that the system has no memory.There is no feedback from the external environment, and this is the evolution of a free particle.Correspondingly,a quantum state suffering from environmental impact is described forα ̸=1.As shown in Fig.1,for the given angular frequencyw0,we find the smallerαis, the smaller change of real part ofc0would be.This result means that with the enhancement of memory, the antiinterference ability of the system is enhanced.Meanwhile, it is found that the change ofαwill affect the amplitude of the real part ofc0.The amplitude of real part ofc0becomes bigger with the decrease ofα.Especially,the value of amplitude will be greater than 1.This is consistent with the total probability of the system we mentioned earlier is greater than 1.Similarity, we plot Fig.2 to show the dependency between real part ofc1and the parameterα.The influence ofαon the real part ofc1is consistent with that of the real part ofc0.The rate of real part ofc1becomes smaller with the decrease ofα.Meanwhile,the smallerαis,the bigger amplitude of real part ofc1would be.
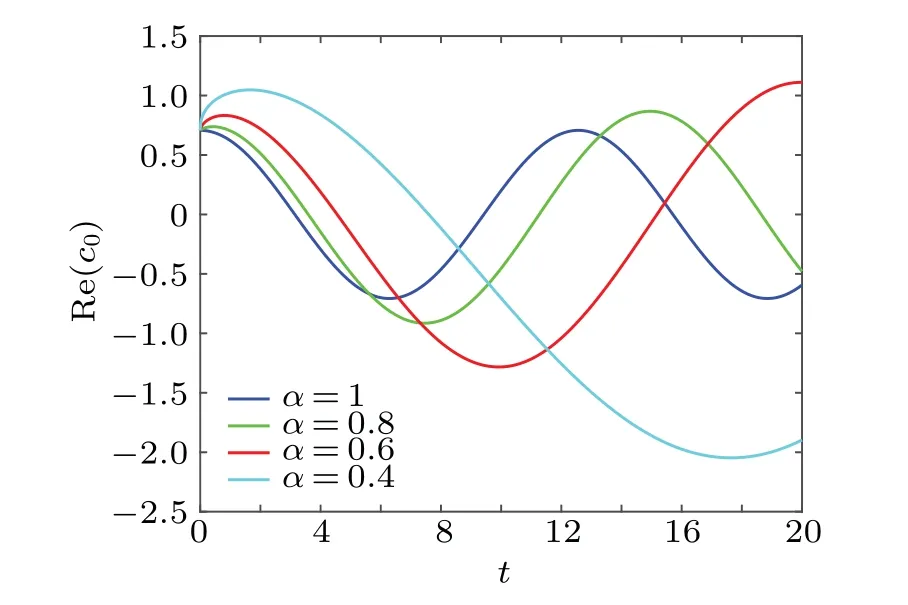
Fig.1.The real part of c0 as a function of t for different α with w0=0.5,i →iα.

Fig.2.The real part of c1 as a function of t for different α with w1=0.8,i →iα.
More specifically, we use fidelity to quantify the difference between the final state and the initial state, which is defined as
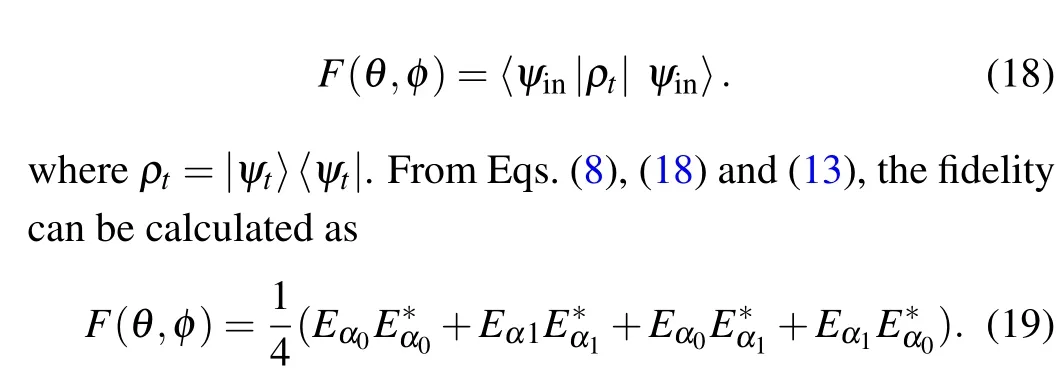
The behaviors of fidelity as a function of the parametertfor differentαare shown in Fig.3.Considering the fluctuation of particles,the fidelity is oscillation.The smallerαis,the larger the maximum value of fidelity is.In particular,the fidelity will be greater than 1 range withα<1.This phenomenon cannot be explained.
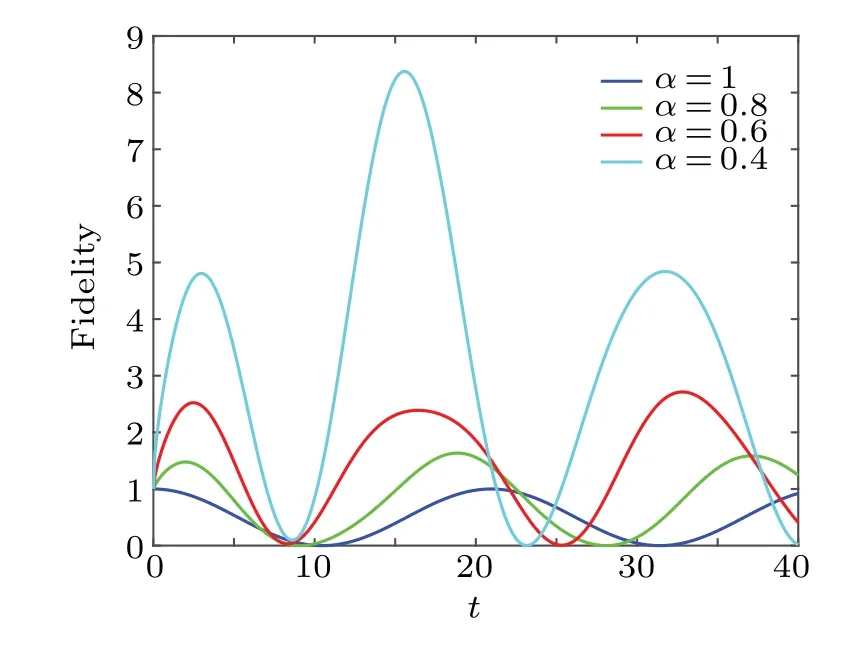
Fig.3.The fidelity F as a function of t for different α with w0 =0.5,w1=0.8, i →iα.
We have discussed the evolution of a quantum state by using Eq.(1).Considering the non-Markovian environment,the result is unacceptable.Now,we will use Eq.(2)to discuss the evolution of a single quantum state.From Eqs.(10) and(6),the final result of Eq.(2)can be expressed by

It is not difficult to prove that the total probability as time approaches infinity is equal to 0.[43]This result is in line with the quantum dissipative system.Likewise,we plot Fig.3 to show the evolution of a quantum state.Figure 3 shows the result of the real part ofc0as a function of the parametertfor differentαwithw0=0.5.It can be easily found that quantum states lose their volatility whenα ̸=1.With the passage of time,the value of the real part ofc0finally approaches 0.It indicates that the result of the time evolution of a quantum state is the disappearance.The quantum state finally loses all information under the interference of the environment.Meanwhile, It is found that the change ofαwill influence the time required for quantum state to disappear.The smallerαis, the slower the disappearance of the quantum state would be.This shows that the memory effect enhances the anti-interference ability of the system.Similarly,we plot Fig.4 to show the dependency between real part ofc1and the parameterα.The evolution of real part ofc1with time is consistent with that of the real part ofc0.
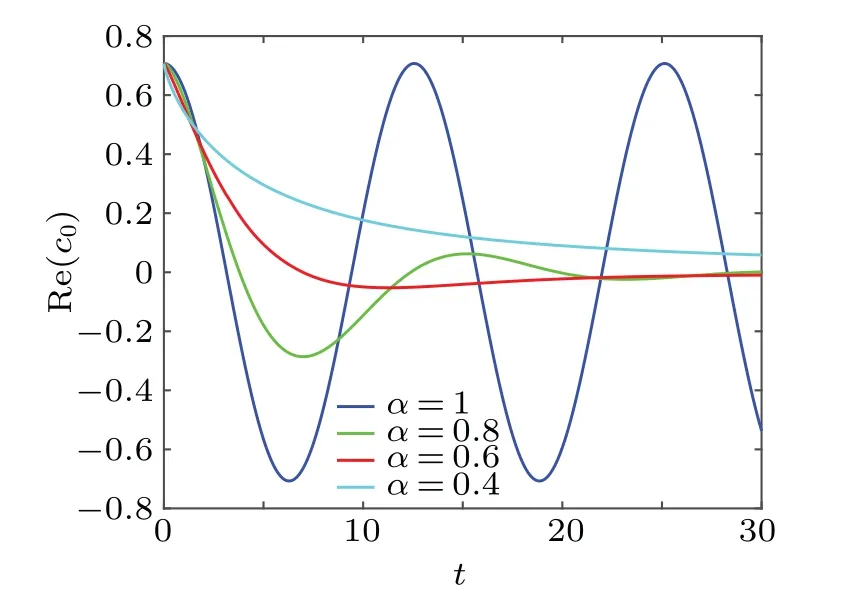
Fig.4.The real part of c0 as a function of t for different α with w0=0.5,i →i.
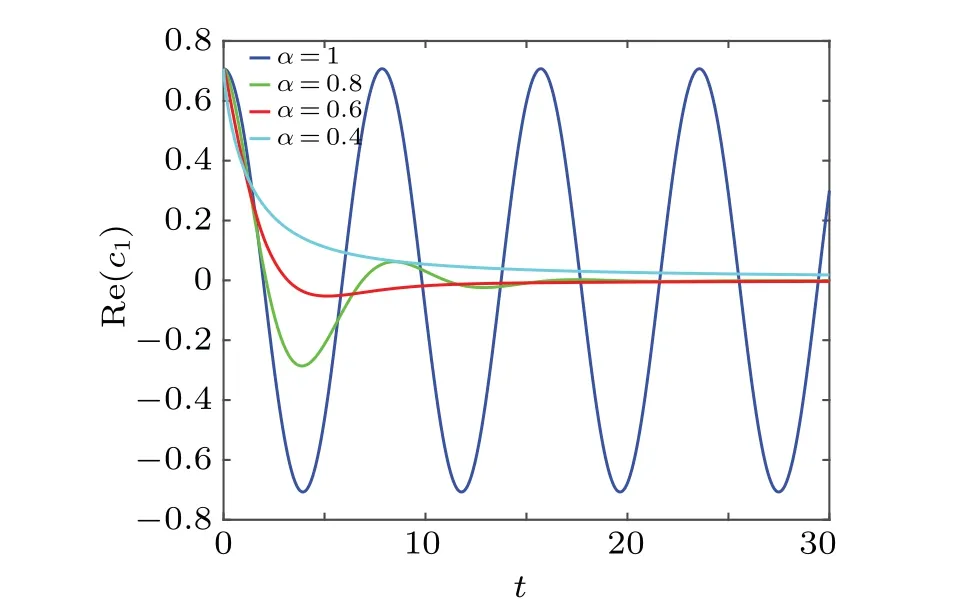
Fig.5.The real part of c1 as a function of t for different α with w1=0.8,i →i.
Similarly,from Eqs.(22)and(18)the fidelity can be obtained by
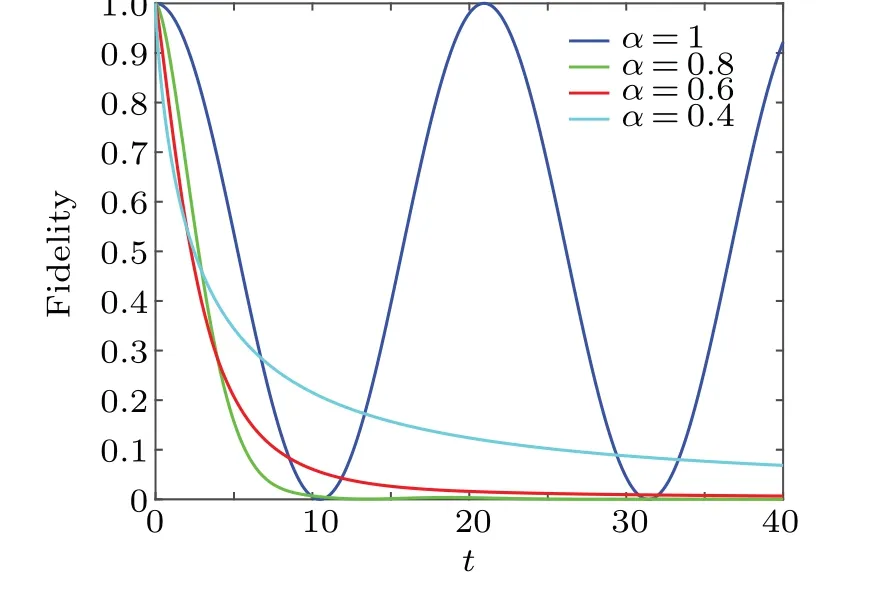
Fig.6.The fidelity F as a function of t for different α with w0 =0.5,w1=0.8, i →i.
Figure 6 shows the result of the fidelity as a function oftfor differentα.As one might expect,the fidelity ranges from 1 to 0 over time in the memorized circumstance(i.e.,η ̸=1).Interestingly,it is found that the fidelity will increase with the enhancement of memory.This implies that memory can effectively reduce the impact of external environment on the system.This is consistent with the existing physics.
4.Conclusion
In summary, we studied the time fractional Schrödinger equation from the perspective of non-Markovian environment.Firstly,we prove mathematically that it is meaningless to study the memory of time fractional Schrödinger equation with time derivative 1<α ≤2.Then, we find it inappropriate to raise i to the order of the time derivative.If the imaginary unit i is not processed with the corresponding fractional order, the quantum state influenced by the environment gradually loses information until it vanishes entirely.Simultaneously,the augmentation of memory bolsters the system’s resilience against environmental impacts, aligning well with the evolution of quantum states in non-Markovian environment.However, if raising i to the order of the time derivative,quantum state remains volatile.The influence of memory is reflected in the wave packet diffusion and amplitude of particles.With the enhancement of memory, the wave packet diffusion of particles will slow down.Meanwhile, the amplitude of quantum state will increase until it is greater than 1.Most notably, quantum states perform more proficiently in the presence of memory,not only retaining information under environmental influence but also accumulating additional information — a phenomenon that defies explanation within a quantum dissipative system.Finally, we hope that our research would be helpful for the practical applications of time fractional Schrödinger equation.
Acknowledgement
Project supported by the National Natural Science Foundation of China(Grant No.11274398).
- Chinese Physics B的其它文章
- Quantum synchronization with correlated baths
- Preparing highly entangled states of nanodiamond rotation and NV center spin
- Epidemic threshold influenced by non-pharmaceutical interventions in residential university environments
- Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk
- Dynamics and synchronization in a memristor-coupled discrete heterogeneous neuron network considering noise
- Spatial search weighting information contained in cell velocity distribution

