Dynamical behavior of memristor-coupled heterogeneous discrete neural networks with synaptic crosstalk

Minglin Ma(马铭磷), Kangling Xiong(熊康灵), Zhijun Li(李志军), and Shaobo He(贺少波)

School of Automation and Electronic Information,Xiangtan University,Xiangtan 411105,China

Keywords: discrete memristor,synaptic crosstalk,coexisting attractor,phase synchronization

1.Introduction

Neurons are the fundamental units of structure and function in the nervous system, and they form neural networks through various types of connections.[1]Neural networks play a crucial role in fields such as signal processing,[2,3]associative memory,[4,5]robot control,[6]and image processing.[7–9]As is widely known, a memristor is a device that describes the relationship between charge and flux.[10]Since its development by HP Laboratory in 2008, memristors have found extensive applications in neural networks,[11–15]image encryption,[16,17]chaotic systems,[18–24]and more.Due to their unique biomimetic properties, such as nanoscale size, low power consumption, and non-volatility, continuous memristors are considered the optimal choice for simulating synapses in analog form.[25–30]Compared to conventional electronic synapses, neural networks based on memristive synapses can more effectively mimic the complex firing activity of biological neural networks.For instance,memristor-coupled neural networks can generate grid multiscroll attractors,[31–34]diverse chaotic attractors that are employed in image encryption.[35]Locally active memristorbased Hopfield neural networks can exhibit more complex dynamical behaviors.[36]

So far, several models of discrete neurons, such as the Chialvo model,Rulkov model,Izhikevich model,and Kinouvhi and Tragtenberg (KT) model, have been proposed.Discrete neuron models have advantages over continuous neuron models in terms of computational time, computational resources, and data storage.[37–42]Therefore, discrete neuron models are more suitable for simulating large-scale neural networks and conducting general research, such as generating chaotic trajectories, pattern recognition, and analyzing synchronized firing behaviors.[43–51]As a result, research on discrete neurons has become a hot topic in recent years.In discrete memristor-coupled neural networks, complex dynamical behaviors have been discovered,including coexisting attractors,[52–56]synchronization transitions,and synchronization coexistence.[57,58]Additionally, Luet al.[59]investigated fractional-order neural networks based on discrete memristors and found that this system exhibits richer dynamical behaviors compared to integer-order neural networks.

Synaptic crosstalk refers to the spillover of neurotransmitters from one synapse to another or the lateral diffusion of receptors from one spine to neighboring spines.It has profound implications for neural signal transmission.[60,61]Increasing evidence suggests the widespread occurrence of synaptic crosstalk among neuronal synapses.Considering synaptic crosstalk,Lenget al.proposed a heterogeneous neural network (HNN) and analyzed the dynamical behavior of the HNN.[62]Liet al.proposed an associative memory circuit based on memristors that takes into account synaptic crosstalk and demonstrated its impact on memory function.[63]Based on the above research, we found that crosstalk can affect the dynamic behavior and associative memory energy of neural networks.Therefore,exploring the behavior of discrete neural networks with crosstalk behavior has practical significance.

Inspired by the aforementioned papers, it is proposed that discrete memristors are used to mimic synapses, coupling a Chialvo neuron and a KTz neuron.Considering the crosstalk behavior between synapses, a memristor-coupled HDNN model is constructed and the dynamical behavior of this neural network is analyzed.The structure of this paper is as follows: In Section 2, a novel discrete memristor model is introduced.In Section 3, the memristor-coupled HDNN model with synaptic crosstalk is proposed.Section 4 investigates the coexistence behavior of the HDNN.In Section 5,the phase synchronization behavior of the memristor-coupled HDNN under different crosstalk strengths is discussed.Finally,conclusions are provided.

2.Discrete memristor

2.1.Discrete memristor model and its characteristics

In this study, we employ two discrete memristors to mimic synapses, coupling two different types of neurons: a KTz neuron and a Chialvo neuron.The topological structure of this neural network is illustrated in Fig.1.The model of the memristor synapse can be expressed by

wherei(n) andv(n) respectively represent the input current and voltage at both ends of the discrete memristor, andW[q(n)] is the memristor inductance value of the memristor.α,γ,δ,βare four memristor parameters.In this paper, we setα= 0.1,β= 1,δ= 5,γ= 1.To model the phenomenon of synaptic crosstalk, we consider the interaction between two memristors.The weights of the two discrete memristor synapses can be described as follows:

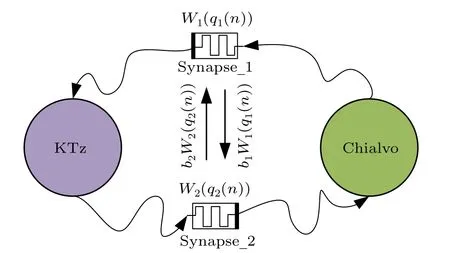
Fig.1.Topological structure of the HDNN with synaptic crosstalk.

2.2.Pinched hysteresis loops

Under the condition of an input sinusoidal voltage signalv(n)=Asin(wT(n)), and the initial value of the discrete memristorq(1)=-2,the voltage–current characteristic curve of the discrete memristor is shown in Fig.2.By changing the amplitude of the sinusoidal voltage signal, figure 2(a) illustrates an “8” shaped hysteresis loop crossing the origin, and the area of the loop gradually increases with the increase in amplitude.By varying the frequency of the sinusoidal voltage signal,figure 2(b)shows the hysteresis loop gradually shrinking.As the frequency increases,the area of the hysteresis loop gradually decreases until it becomes a single-valued function.Therefore,this discrete memristor complies with the definition of a generalized memristor.

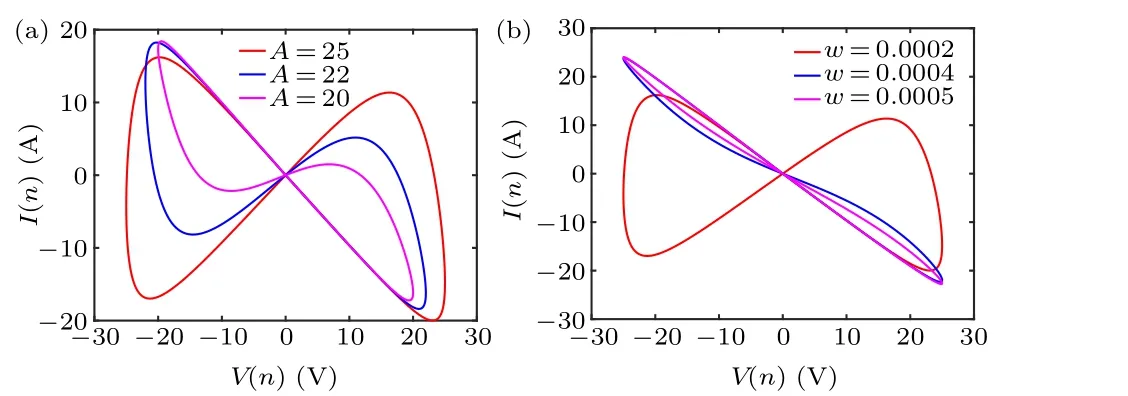
Fig.2.Hysteresis loop of the memristor: (a)w=0.0002,A=20,22,25,(b)A=25,w=0.0002,0.0004,0.0005.

3.Memristor-coupled HDNN

3.1.KTz neurons and Chialvo neurons

The model of three-dimensional KTz neurons is as follows:[64]

wherex(n) represents the membrane potential of the neuron,y(n)denotes the recovery variable,z(n)represents the slow total ion current.a,d,t,g,handuare parameters that control the firing patterns of the neuron.

The model of two-dimensional Chialvo neurons is as follows:[65]

wherex(n) represents the membrane potential of the neuron,y(n)denotes the recovery variable,a,bandcare parameters,andI(t)can be regarded as the external input current.

3.2.Model of the memristor-coupled HDNN

The model of the memristor-coupled HDNN with synaptic crosstalk is represented by Eq.(5),wherekis the coupling strength of the neural network,b1andb2are the crosstalk strengths of the system.The remaining parameters of the system are as follows:a= 0.6,t= 0.35,c= 0.1,c1= 0.28,a1=0.9,d=0.4,d1=0.03,r=0.6,k=0.2,g=0.008,h=0.008,u=-0.3,δ=5,γ=2.

3.3.Analysis of equilibrium points

The corresponding Jacobian matrix is

The equilibrium points and eigenvalues for different levels of crosstalk strength are shown in Table 1.

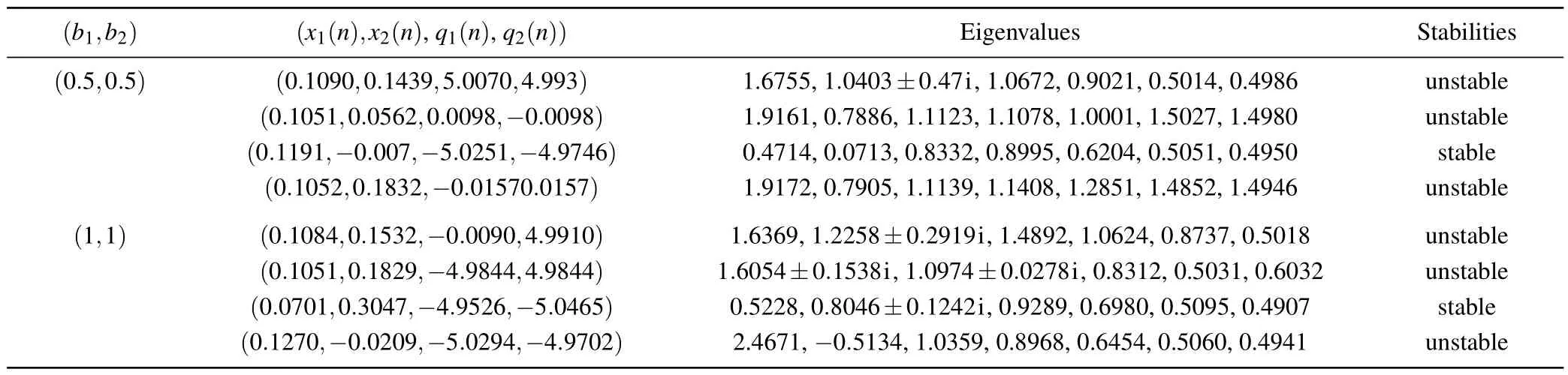
Table 1.Equilibrium points,corresponding eigenvalues and stabilities.

The stability of equilibrium points in chaotic systems significantly influences the dynamical behavior.The stability of the equilibrium points can be determined based on the eigenvalues.When the eigenvalues lie within the unit circle, the equilibrium points are stable;otherwise,they are unstable.

To analyze the impact of crosstalk strength on the dynamics of the memristor-coupled HDNN,certain system parameters are held constant as follows:a=0.6,t=0.35,c=0.1,c1=0.28,a1=0.9,d=0.4,d1=0.03,r=0.6,g=0.008,h=0.008,andu=-0.3.

Fig.3.Bifurcation diagram and Lyapunov exponent plot with respect to crosstalk strength b1.(a) Bifurcation diagram with respect to b1 for the initial condition (-1,1,1,-1,1,1,1); (b) Lyapunov exponent plot with respect to b1 for the initial condition(-1,1,1,-1,1,1,1);(c)bifurcation diagram with respect to b1 for the initial condition(-1,1,1,-1,1,-1,1);(d) Lyapunov exponent plot with respect to b1 for the initial condition(-1,1,1,-1,1,-1,1).

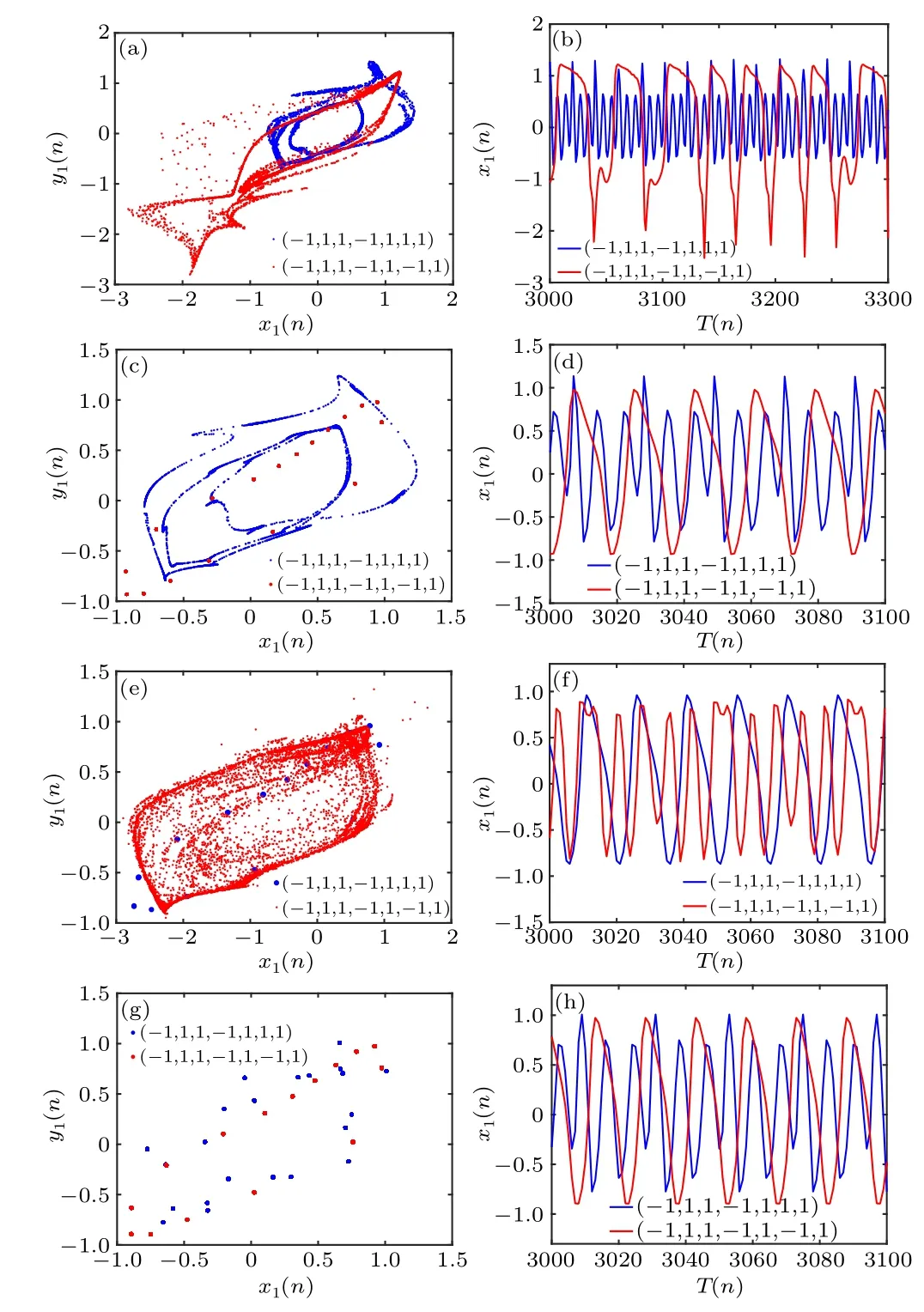
Fig.4.Phase portrait in the x1–y1 plane and time series plot of x1 for different crosstalk strengths b1.[(a)and(b)]b1=2,coexistence of chaotic attractors and chaotic attractors; [(c) and (d)] b1 =1.15, coexistence of chaotic attractors and periodic attractors;[(e)and(f)]b1=-0.88;coexistence of periodic attractors and chaotic attractors;[(g)and(h)]b1=1.03,coexistence of periodic attractors and periodic attractors.

4.Impact of crosstalk strength on multistability

4.1.Impact of crosstalk strength b1

When the coupling strengthk= 0.2 and the crosstalk strengthb2=0.2,considering two different initial conditions(-1,1,1,-1,1,1,1) and (-1,1,1,-1,1,-1,1), the bifurcation diagram and Lyapunov exponent plot with respect to the crosstalk strengthb1are shown in Fig.3.Obviously,this system shows the characteristics of multistability.To provide a more visual representation of the system’s multistability, we plot the different coexisting attractors under different crosstalk strengths in Fig.4.We observe the coexistence of chaotic attractors with chaotic attractors,chaotic attractors with periodic attractors,periodic attractors with chaotic attractors,and periodic attractors with periodic attractors in the system.

4.2.Impact of crosstalk strength b2

When the coupling strengthk= 0.2 and the crosstalk strengthb1=0.85,considering two different initial conditions(-1,1,1,-1,1,1,1) and (-1,1,1,-1,1,-1,1), the bifurcation diagram and Lyapunov exponent plot with respect to the crosstalk strengthb2are shown in Fig.5.Different coexisting attractors under different crosstalk strengths are shown in Fig.6.It is observed that under this condition,the system exhibits the coexistence of chaotic attractors with chaotic attractors,chaotic attractors with periodic attractors,periodic attractors with chaotic attractors, and periodic attractors with periodic attractors.

5.Impact of crosstalk strength on phase synchronization

When studying the influence of different crosstalk strengths on the phase synchronization of neurons, the phase of the neurons can be expressed by the following equation:With a fixed value ofk=0.2 andb1=0.85,when the crosstalk strengthb2= 0.5, as shown in Figs.7(a) and 7(b), the firing pattern of the neurons is characterized by spike firing,and the two neurons are not synchronized.In Figs.7(c)and 7(d),it can be seen that as the crosstalk strengthb2decreases to 0.1, the two neurons gradually start to synchronize.When the crosstalk strengthb2=-1, as shown in Figs.7(e) and 7(f), one neuron exhibits firing in chaotic clusters, while the other neuron exhibits spike firing, and phase synchronization is achieved.

Fig.5.Bifurcation diagram and Lyapunov exponent plot with respect to crosstalk strength b2.(a) Bifurcation diagram with respect to b2 for the initial condition (-1,1,1,-1,1,1,1); (b) Lyapunov exponent plot with respect to b2 for the initial condition(-1,1,1,-1,1,1,1);(c)bifurcation diagram with respect to b2 for the initial condition(-1,1,1,-1,1,-1,1);(d) Lyapunov exponent plot with respect to b2 for the initial condition(-1,1,1,-1,1,-1,1).

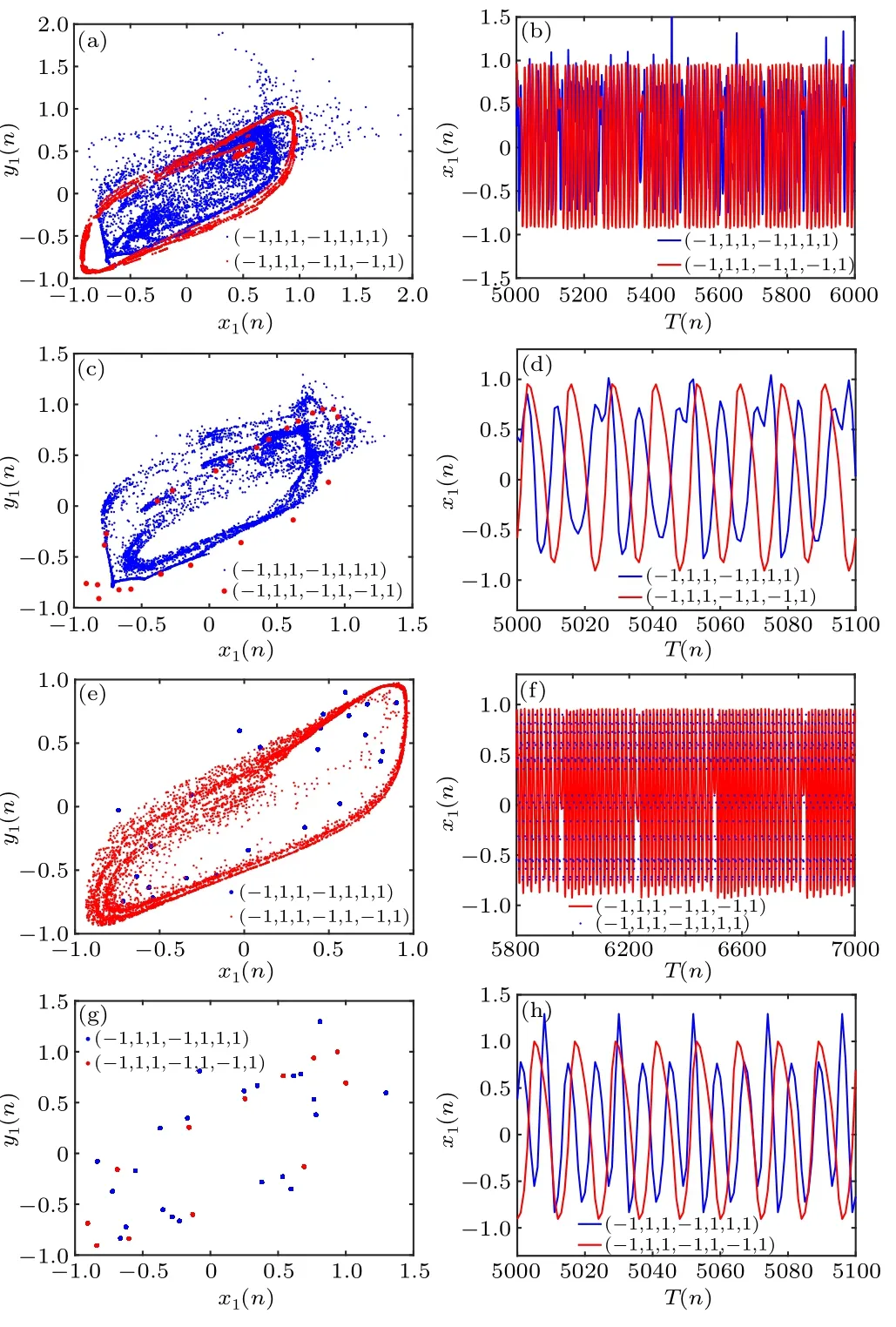
Fig.6.Phase portrait in the x1–y1 plane and time series plot of x1 for different crosstalk strengths b2.[(a) and (b)] b2 = 1, coexistence of chaotic attractors and chaotic attractors; [(c) and (d)] b2 =1.255, coexistence of chaotic attractors and periodic attractors;[(e)and(f)]b2=1.3,coexistence of periodic attractors and chaotic attractors; [(g) and (h)]b2=-0.25,coexistence of periodic attractors and periodic attractors.

With a fixed crosstalk strength ofb2= 0.2, when the crosstalk strengthb1=0.1, as shown in Figs.8(a) and 8(b),it can be observed that the phase of the two neurons is not synchronized.As depicted in Figs.8(c) and 8(d), when the crosstalk strengthb1decreases to-0.5,their phases gradually synchronize.Further reducing the crosstalk strength to-1.2,both neurons exhibit spike firing patterns and achieve phase synchronization.

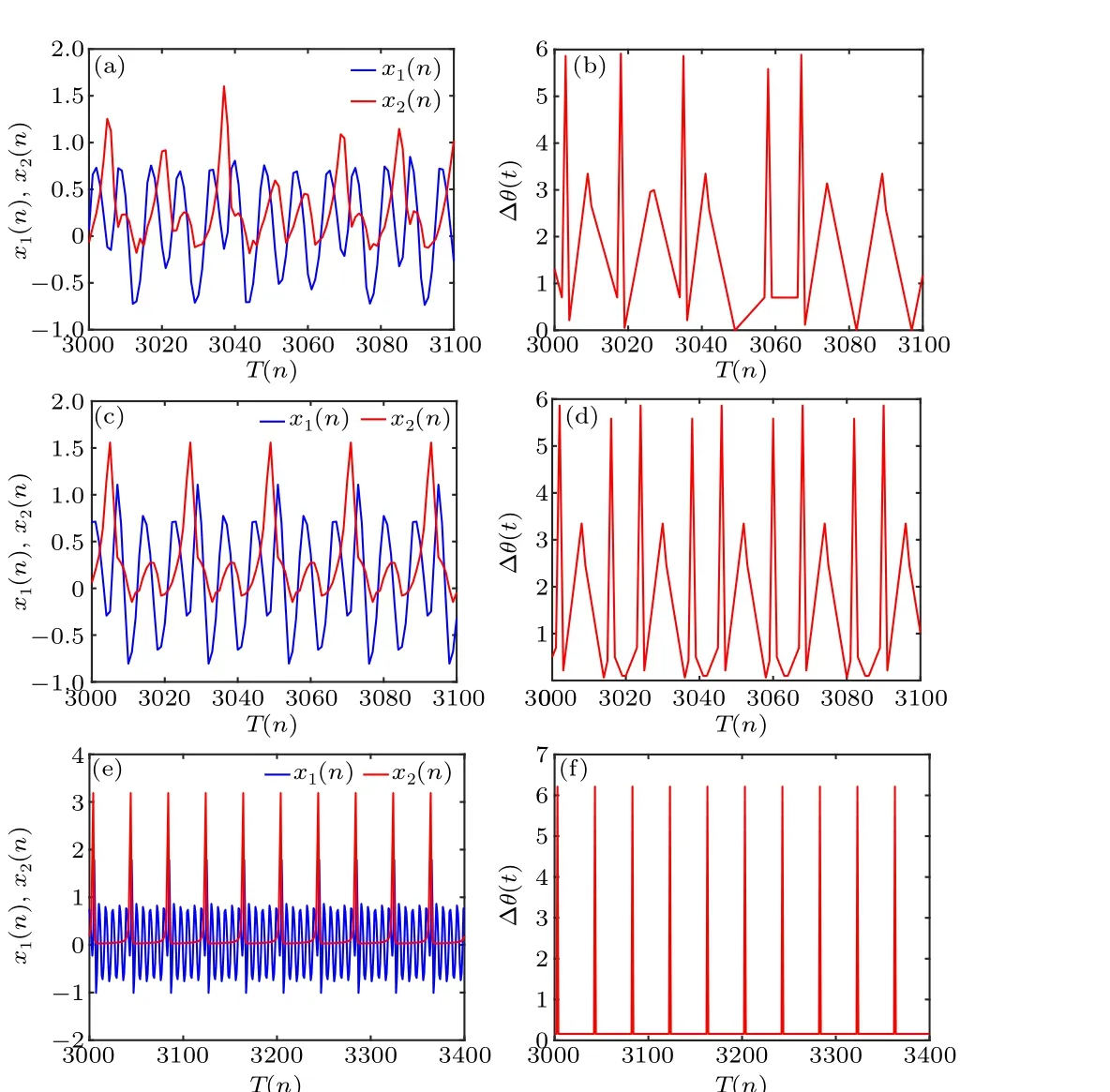
Fig.7.Synchronization transition of the memristor-coupled HDNN with a fixed crosstalk strength of b1.[(a) and (b)] b2 = 0.5; [(c) and (d)]b2=0.1;[(e)and(f)]b2=-1.

Fig.8.Synchronization transition of the memristor-coupled HDNN with a fixed crosstalk strength of b2.[(a) and (b)] b1 =0; [(c) and (d)]b1=-0.5;[(e)and(f)]b1=-1.2.

6.Conclusion

In this paper, we propose a memristor-coupled HDNN,which consists of a two-dimensional Chialvo discrete neuron,a three-dimensional KTz discrete neuron, and two memristor synapses.The synaptic crosstalk within the network is modeled by mutual coupling between the memristor synapses.It is found that the system exhibits different attractor coexistence phenomena under different crosstalk strengths, including coexisting chaotic and chaotic attractors, coexisting chaotic and periodic attractors, and coexisting periodic and periodic attractors, which reveals the multistability behavior of the memristor-coupled HDNN.Furthermore, in this paper,the synchronous firing behavior between two discrete neurons is investigated by varying the crosstalk strength.

Acknowledgments

Project supported by the Key Projects of Hunan Provincial Department of Education (Grant No.23A0133), the Natural Science Foundation of Hunan Province (Grant No.2022JJ30572),and the National Natural Science Foundations of China(Grant No.62171401).