Properties of focused Laguerre–Gaussian beam propagating in anisotropic ocean turbulence

Xinguang Wang(王新光), Yangbin Ma(马洋斌), Qiujie Yuan(袁邱杰), Wei Chen(陈伟),Le Wang(王乐), and Shengmei Zhao(赵生妹),3,4

1College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

3Key Lab of Broadband Wireless Communication and Sensor Network Technology(Ministry of Education),Nanjing University of Posts and Telecommunications,Nanjing 210003,China

4National Laboratory of Solid State Microstructures,Nanjing University,Nanjing 210093,China

Keywords: vortex beam,orbital angular momentum,focusing mirror,anisotropic turbulence

1.Introduction

Owing to the orthogonality and completeness of orbital angular momentum (OAM),[1–3]which could theoretically form an infinite-dimensional Hilbert space, there are an infinite number of quantum bit bases that can be loaded with information.The carrier wave carrying OAM is often referred to as vortex beams that have a wide range of applications in optical tweezers, particle manipulation, and quantum entanglement.[4–7]In particular, the efficiency and performance of vortex beam-based communication systems can be greatly improved in that the number of signal bits each photon carries is log2N,[8]whereNis the number of OAM modes that can be available for information mulplexing,which is one of the research hotspots in the field of free-space optical communication.[9–11]

It is worth noting that there appears to be distortion of the signal OAM mode and crosstalk between different energy states of adjacent OAM modes during the transmission of the vortex beam in turbulent medium, reducing the channel capacity of the OAM information transmission system severely, where the effect of refractive index fluctuation of turbulent medium is crucial.[12–14]Then, it is essential to take the influence of turbulent medium into account in designs and applications of free-space optical communication links, and the mitigation of the turbulence effect has aroused considerable interests.Adaptive optics (AO)[15–17]is one of the effective methods to alleviating turbulence and the distorted beam profile is measured to derive a sequential error correction pattern, which is then sent through a feedback loop to the beam correction module to compensate for the beam distortion in a typical AO system.In addition, special beams with approximately non-diffracting properties,such as Bessel–Gaussian beams,[18]Hankel–Bessel beams (HB),[19]Airy vortex beams,[20]and Lommel–Gaussian beams,[21]are highly tolerant of turbulence and have been found to offer advantages over diffractive beams.

Recently, the application of the focused mirror method for alleviating turbulence effects has attracted much attention of researchers.Zhouet al.numerically simulated the propagation characteristics of Gaussian vortex beams with mirror and without the mirror in atmospheric turbulence and found that the former could outperform significantly the latter under the same turbulent environment.[22]Yanet al.investigated the crosstalk properties of focused vortex beams in atmospheric turbulence combining theoretical derivation and phase screens and found that focused LG beam is more resistant to turbulent interference than the unfocused one.[23]Wanget al.explored the focused mirror method and circular aperture method to reduce OAM crosstalk of LG beams in plasma turbulence and demonstrated that the focused mirror method can be used to mitigate the effects of OAM crosstalk from turbulence better than the circular aperture one.[24]Moreover,there are focused annular vortex beams,[25]focused Bessel beams,[26]and other focused vortex beams that have high tolerance to turbulent interference and potentially other properties.[27]

Compared to transport media such as atmospheric turbulence, oceanic turbulence is more complex and has a greater impact on the vortex beams passing through it.We anticipate that the performance of an LG beam with focusing mirror resisting for turbulence will have great potential applications in underwater wireless optical communication.In this paper,we study the properties of a focusing LG beam propagating in anisotropic ocean turbulence,and analyze the effect of the focusing mirror on reducing the interference of turbulent ocean through analytical derivation and numerical simulation, so as to provide useful theoretical support and reference for applications and development of underwater wireless optical communication.

In this article,the mathematical model of channel capacity based on a focused LG beam in anisotropic ocean turbulence is established.Then, the properties of the focused LG beam are studied numerically, including the influence of different light source parameters and oceanic turbulence parameters on the beam channel capacity.In addition,a comparative analysis is conducted on the system performance of underwater communication links with focused LG beams, unfocused LG beams,and HB beams,respectively.

2.Theoretical derivation

The complex amplitude of the focused LG beam at the initial plane can be expressed as[23,24]

Then,according to the Huygens–Fresnel integral expression,we can obtain the complex amplitude of the focused LG beam at distancezin free space as

There appears to be the beam phase distortion during the beam transmission in the seawater medium due to the disturbance of oceanic turbulence,which results in the dispersion of the signal OAM mode and crosstalk between adjacent OAM modes.The complex amplitude of the focused LG beam in oceanic turbulence can be expressed as

whereψ1(r,ϕ,z)represents the random complex phase disturbance caused by oceanic turbulence.From the superposition theory of spiral harmonics,the complex amplitude of the beam at the receiving plane can be expressed as a superposition of beams with different OAM modes:

whereRis the aperture size of the receiver.The above equation represents the signal OAM mode detection probability if the received OAM modemis equal to the transmitted signal modem0,otherwise it represents the crosstalk probability whenm ̸=m0.

Given the smooth discrete memoryless system proposed by Shannon’s information theory, according to Eq.(18), the channel capacity of the focused LG beam in oceanic turbulence can be expressed as[31–33]

wherem0is the topological charge of the signal OAM mode varying from 0 tolm,N=lm+1 denotes the number of transmission channels in the oceanic communication system.P(m0) denotes the probability of sending a topological chargem0, andP(m|m0) denotes the conditional probability of receiving topological charge ofm(m ̸=m0).Combining Eq.(18) with Eq.(20) and utilizing the Arimoto–Blahut algorithm,[34,35]we can calculate the channel capacity of the system based on the focused LG beam in oceanic turbulence.

3.Results and discussion

In this section, the channel capacity of the focused LG beam in oceanic turbulence is analyzed by numerical simulations using the analytical formulae derived in Section 2.Unless stated otherwise,the parameters selected in this paper areλ=532 nm,ω0=2×10-2m,p=0,ε=10-5m2·s-3,χT=10-8K2/s,l0=0.001 m,L0=10 m,PrT=0.41,PrS=700,ϖ=-4,ξ=2,N=11,R=3×10-2m,f=200 m, andz=200 m.

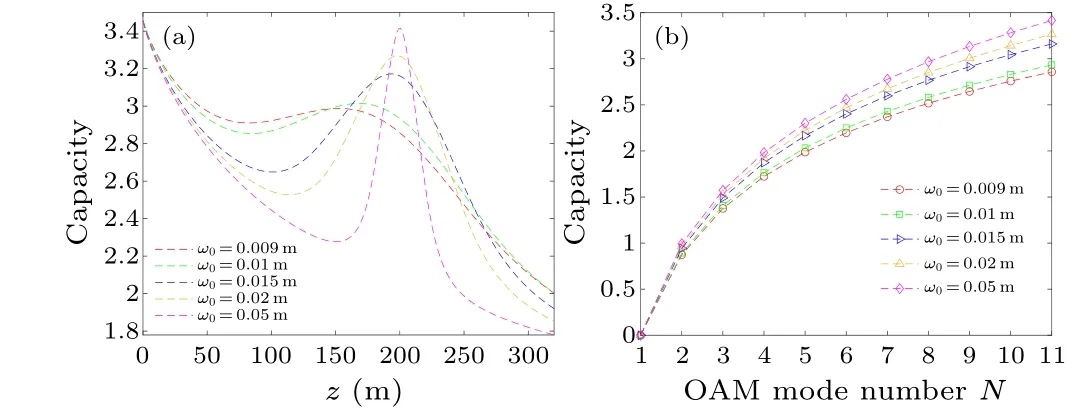
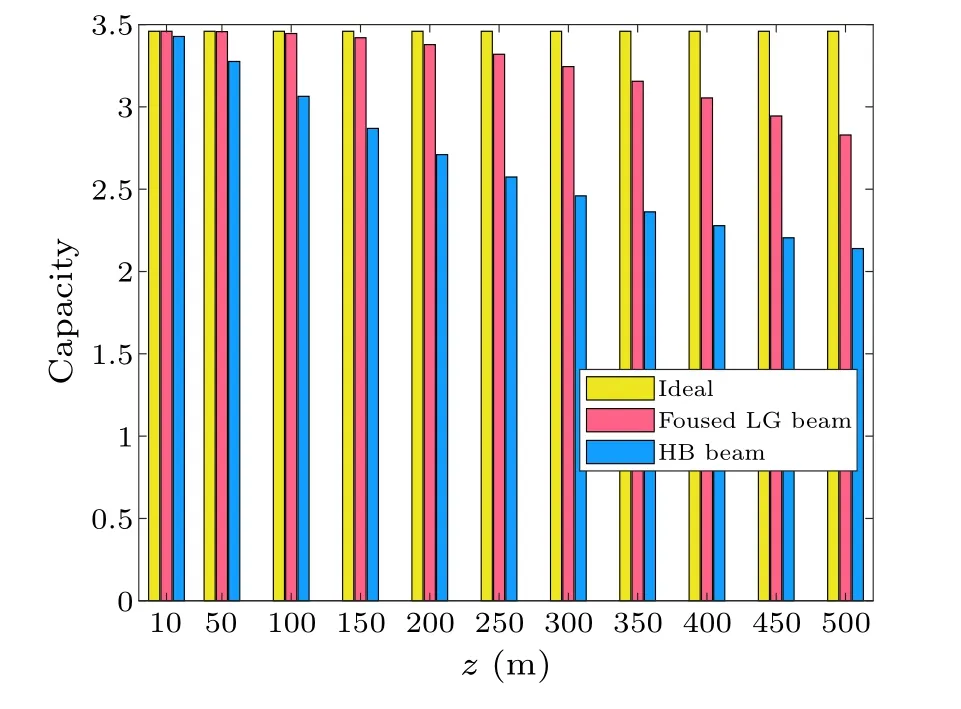
Figure 1 shows the intensity distribution, phase distribution and the focusing behavior of beams propagating in free space withm0=1.When the value of the geometric focal lengthfis set to+∞,we can obtain numerical simulation results for the unfocused LG beam.Figures 1(a)and 1(b)show the 3D intensity distribution and its cross lines (y= 0), together with the phase distribution of the focused LG beam(the top line) and the unfocused LG beam (the bottom line)transmitted at 20 m.As can be seen, comparing Figs.1(a3)and 1(b3), the focusing mirror causes the beam to produce a phase burst of sizeπat the focal point.This phenomenon is a property of geometrical optics whose physical mechanism originates from transverse spatial confinement, which introduces a spread in the transverse momenta through the uncertainty principle, and hence a shift in the expectation value of the axial propagation constant.[36,37]Furthermore,a comparison of the intensity distributions of two beams,as shown in the left two columns of Figs.1(a) and 1(b), indicates that during transmission with a focusing mirror, its spatial confinement effect on the beam will concentrate the size distributions in a smaller region and significantly increase the beam intensity.On the other hand, we calculate in Fig.1(c) the focusing behavior of the focus LG beam near the geometric focus underf=200 m in thex–zplane.Herefandf0represent the geometric focal length and the actual focal length that correspond to the geometric focus and actual focus in free space,respectively.It is found that the intensity distribution of the focused LG beam shows a clear evolutionary process of focusing first and then diverging in the vicinity of focus.Meanwhile, the position of the maximum intensity along the propagation direction locates before the geometric focus,i.e.,f0

To learn about the influence of the focusing property on the channel capacity near the focus point in oceanic turbulence,we display in Fig.2 the channel capacity versuszunder differentλfor the unfocused LG beam,as well as the focused LG beam with the given value off.From Figs.2(a)and 2(b)we can see that the channel capacity of both systems based on these two beams initially decreases with a growingzbecause the impact of turbulence on the beams becomes more significant with the increment ofz.Aszfurther increases,this evolutionary trend will continue to apply to the unfocused LG beam,but not to the focused LG beam with a focusing mirror.For the focused LG beam,it is clear from Figs.2(a)and 2(b)that the capacity of the system begins to increase to the maximum and then decrease aszincreases near the focus point.Notably,the value point ofzcorresponding to the maximum channel capacity is not exactly equal to the geometric focal length,but rather precedes it, which appears much more evident for a largerfwithλfixed in comparison between Figs.2(b)and 2(a).Also,the difference mentioned above is more apparent with a largerλin Fig.2(b).Besides the influence arising from the oceanic turbulence, the physical mechanism of this result is mainly derived from the focal shift phenomenon of the focused LG beams as shown in Fig.1(c).Nevertheless, the channel capacity of the system can still achieve high optimization at the geometric focal plane,as illustrated in Figs.2(a)and 2(b),despite the effect of focal shift on the position of the maximum channel capacity in the vicinity of the focus, andz=fis set mainly for the simulation and analysis in this paper.

One can also find from Fig.2 that the longer theλ, the larger the system capacity because the beam with a longerλhas lower scintillation, thus bringing about a greater system channel capacity.It is worth noting that whenftakes different values,the modulation effect of differentλon channel capacity varies at the geometric focus, which is much more evident in Fig.2(b)than in Fig.2(a).In Fig.2(a), for the focused LG beams transmitting in the near field with shortz,even though the scintillation of beams with differentλvaries,their Rayleigh distance is much larger thanfthus the beams all have better focusing effect,[26,39]then the interference of scintillation on beam transmission can be neglected compared to the focusing effect, so the capacity of beams with differentλtends to be the consistent.However, the focusing effect of beam gradually weakens with the increment off, and the influence of the light intensity flicker effect on the system gradually surpasses that of the focusing effect.Therefore, as the transmission distance further increases in the far field with largez, the longer theλ, the greater the capacity of the system at the geometric focus as shown in Figs.2(b) and 2(c).In addition,obviously,the numerical results indicate superior performance utilizing the focused LG beam compared to the unfocused one on enhancing the channel capacity under the same transmission conditions atz=f,due to the smaller beam size as shown in Fig.1 and less exposure to the turbulence thus resulting in lower negative interference for using focused LG beams.

Fig.2.The channel capacity of the unfocused LG beam,as well as the focused LG beam with(a) f =200 m,(b) f =600 m,(c) f =z in oceanic turbulence versus transmission distance z under different wavelength λ.

Figure 3 displays the channel capacity of the focused LG beam with different waist radiusω0in oceanic turbulence underf=200 m versusz, as well as number of transmission channelsNatz=200 m.As is shown in Fig.3(a),the channel capacity of the system under differentω0decreases with increasingzfirst,and then increases aszfurther increases,and finally reaches the maximum beforezlocates at the geometric focus.Meanwhile, in the vicinity of focus, the larger theω0of the focused LG beam, the greater the system channel capacity, and the closer the maximum value position to the geometric focus.This is due to the fact that the Rayleigh distance increases with the increase ofω0, bringing about better focusing effect hence higher channel capacity of the communication link.At the same time,the larger theω0,the smaller the focal shift of the beam is, so the consistency between the position of the maximum channel capacity and the geometric focus is higher.On the other hand,Fig.3(b)indicates that for givenω0,with the increase ofN,the more channels the system has to transmit information,the larger the channel capacity is.

Fig.3.The channel capacity of the focused LG beam with different waist radius ω0 in oceanic turbulence under f =200 m versus(a)transmission distance z,as well as(b)number of transmission channels N at z=200 m.

Fig.4.The channel capacity of the focused LG beam for different dissipation rate of mean-squared temperature χT and dissipation rate ε of kinetic energy per unit mass of fluid.

Figure 4 shows the effect of the dissipation rate of the mean-squared temperatureχTand the dissipation rate of the kinetic energy per unit mass of fluidεon the channel capacity of the beam.AsχTandεmount,the channel capacity diminishes and increases respectively in that the turbulent intensity of seawater ascends asχTincreases andεdecreases, magnifying the distortion of the OAM mode wavefront caused by oceanic turbulence,which reduces the channel capacity.

Figure 5 illustrates the effect of the inner scale factorl0and the outer scale factorL0on the beam channel capacity.The increase ofl0and the decrease ofL0augment the channel capacity.Based on oceanic turbulence theory, the turbulence with largerl0induces less significant beam scattering effect.A smallerL0of the turbulence micrifies the random deflection of the beam propagation path and consequently the beam drift,resulting in less wavefront propagation distortion and greater channel capacity,but the effect of the outer scale is not so notable.

Fig.5.The channel capacity of the focused LG beam for different inner scale factor l0 and outer scale factor L0.

Fig.6.The channel capacity of the focused LG beam for different anisotropy factor ξ and temperature-salinity contribution ratio ϖ.

Figure 6 demonstrates the impact of anisotropy factorξand temperature-salinity contribution ratioϖon the channel capacity of the focused LG beam.The channel capacity wanes with a largerϖbecause the salinity fluctuations of seawater have a greater perturbation effect on the capacity than temperature fluctuations.On the other hand,the anisotropic unstable stratified oceanic turbulence power spectrum degenerates to isotropic whenξis equal to 1.Forξ,the larger its value,the stronger the anisotropy and the greater the channel capacity of the beam mainly because higher anisotropy of the turbulent flow minimizes the refractive fluctuations of the beam and amplifies the transmission effect, leading to less interference in the oceanic channel and a larger system capacity.

Fig.7.Channel capacity as a function of z with the focused LG beams and the HB beams.

The comparison of the system channel capacity based on the focused LG beam,the HB beam with diffraction-free characteristics and the ideal condition is depicted in Fig.7.We can see that when the transmission distance is given,the channel capacity of the system based on the focused LG beam and the HB beam is smaller than that of the system under ideal condition due to the interference of turbulence effect.On the other hand,under the same transmission conditions,the channel capacity of the HB beam-based system decreases more sharply with increasing transmission distance than that of the focused LG beam, indicating that the focusing mirror can effectively mitigate the effect of oceanic turbulence and augment the channel capacity of OAM-based underwater optical communication systems.

4.Conclusion

In summary, we have numerically analyzed propagation and properties of a focused LG beam in anisotropic turbulent ocean.The impacts of turbulent ocean parameters and beam source parameters on the channel capacity of the underwater communication link are discussed in detail.The results indicate that the LG beam with mirror has a smaller beam size and higher intensity density during transmission, resulting in strong anti-turbulence and anti-attenuation performance owing to modulation of the focusing mirror.Meanwhile,for the focused LG beam, the location of the maximum channel capacity in the propagation direction is not consistent with the location of the geometric focal plane where the system can still achieve a high degree of optimization for the channel capacity.In addition, it is found that the greater the wavelength or the beam waist radius, and the larger the number of transmission channels applicable to improve the channel capacity for long distance transmission.Further, the capacity of the system increases with the mount of the kinetic energy dissipation rate per unit mass of fluid, the inner scale of seawater turbulence and the anisotropy factor, and decreases with the increase of the mean-squared temperature dissipation rate of oceanic turbulence, temperature-salinity contribution ratio and turbulent outer scale factor.In comparison of the non-diffraction HB beam and the unfocused LG beam,the focused LG beam has larger capacity due to its less beam spreading in the underwater channel.This provides a reference for designs of more robust OAM-based underwater optical communication links.

Acknowledgements

This work was supported by the Science and Technology Innovation Training Program of Nanjing University of Posts and Telecommunications(Grant No.CXXZD2023080),the National Natural Science Foundation of China (Grant Nos.61871234 and 62001249), the Natural Science Foundation of Nanjing University of Posts and Telecommunications (Grant No.NY222133), and the Open Research Fund of National Laboratory of Solid State Microstructures (Grant No.M36055).