Q学习博弈论的WSNs混合覆盖漏洞恢复

张 鸰

（南京交通职业技术学院，江苏 南京 211188）

1 引言

无线传感器网络部署了大量小型智能设备，这些设备形成分布式自组织网络，用于数据收集和管理，可应用于各种领域，如栖息地监测、机器监控、农业精确定位、室内控制、智能报警和军事应用等［1］。然而随机部署、传感器电池耗尽硬件故障、软件缺陷和安全攻击等原因可能会造成覆盖漏洞，严重降低了效率、可靠性和服务质量［2］。

一般通过拓扑控制解决覆盖漏洞，拓扑控制方案的主要研究领域可分为两类：基于节点重新定位的方案和基于功率传输的方案［3］。重新定位方案可分为虚拟力方案、Voronoi 方案和翻转方案。文献［4］提出了一种基于径向虚拟力的重新定位方法，称为分布式自蔓延算法（DSSA）。文献［5］提出了一种基于Voronoi方案和翻转方案混合的自适应检测修复策略，有效综合了Voronoi方案的高精度优点以及翻转方案的简易特性，尽管上述方法在传感器移动和小范围覆盖漏洞恢复方面性能良好，但它在大范围覆盖漏洞中并不有效，因为它需要大量的迭代计算。另外由于独立和分布式的运动，节点重新定位可能会产生新的小覆盖漏洞。在某些情况下，某些节点的运动可能在平均最大化方面无效，并可能耗尽传感器电池电源，降低其到达和修复覆盖漏洞的能力。

为了进一步提升回复覆盖漏洞的效果，考虑将智能算法引入回复策略中。文献［6］提出了一种基于模糊粒子群优化算法的无线传感器网络漏洞修复方法，有效提升了传感器位置优化，从而强化了修复能力。文献［7］提出一种基于Delaunay图的人工蜂群算法控制移动节点的部署策略，通过固定节点形成的Delaunay图先找出覆盖漏洞，估算覆盖漏洞面积并计算出移动节点。文献［8］提出了一种基于深度神经网络与模糊熵相结合的集中式传感器网络漏洞恢复方法，极大地提升了恢复效果。但是上述方法由于需要进行智能优化，因此系统整体能耗成本较大，对于实际应用存在一定难度。另外上述方法考虑的传感器系统均为集中式系统，针对分布式传感器系统中存在的漏洞恢复是否有效还需要验证。

为此，这里提出了一种基于Q学习算法的博弈论的无线传感器网络混合覆盖漏洞恢复方法。设计了一种能够以分散、动态和自治的方式缩小覆盖差距的混合算法，该方法利用基于Q学习算法的博弈论概念，融合了节点重新定位和功率传输调整两种覆盖控制方案。仿真结果证明了提出方法的有效性。

2 相关理论

2.1 系统模型

无线传感器网络可以看作是一个连通图G(V，E)，其中，V是表示节点的顶点集合，E表示节点间链接的边集合。每个传感器可以设计为二维矩形区域中的单位圆盘图，表示为Δ=[xmin；xmax]×[ymin；ymax]，具有感应半径Rs和通信半径Rc。为了简单起见，这里假设S中的所有节点都具有相同的Rc。设S1∈S，S2∈S，如果S1在S2的传输范围内，则这对节点(S1，S2)是双向连接的，令Ei表示传感器节点i的起始能量。假设每个节点都是通过GPS定位的，由于传感器节点的可预测或不可预测的无效性，例如电池电量耗尽或长期放置导致的爆炸，可能会出现覆盖漏洞。覆盖漏洞i可视为半径为和圆心为(xHi，yHi)的圆，此圆表示节点故障发生的区域。通过组合不同圆心和半径的多个覆盖漏洞，可以轻松估计不同形状且复杂的覆盖漏洞。设节点D表示受损节点集，U节点表示未受损节点集，位于空洞区域的每个传感器节点Si∈S属于D节点；否则，将其视为未损坏的节点，属于U节点。

2.2 博弈论

博弈论（Game Theory，GT）是一种用于在不确定环境中做出战略决策的数学模型，它关注的是情景建模，以描述相互依赖代理的可能行为，从而确定最优策略。在处理GT中的竞争情况时，一个代理选择行动的结果在很大程度上取决于其他代理的行动。

定义1（博弈论）［9］：策略形式ξ={τ，Λ，υ} 的博弈由三个基本部分组成，定义如下：

（1）参与者集合τ={1，…，n}，其中，n是参与者的数量。用-i表示不是i的参与者。

（2）行为空间Λ={ Λ1，Λ2，…，Λn}，每个参与者i都有各自的策略Λi，其中Λi是一系列参与者的行为。

（3）效用函数集合υ，其中每个参与者i都有各自的效用函数υi：Λ →R，用来评估参与者的回报。

用Λi表示动作轮廓{a1，a2，…，am}，∀i∈τ。由除i以外的策略配置文件表示，即除i：{ Λ1，…Λi-1，Λi+1，…，Λn}之外的所有参与者的行动集合。

定义2（纳什均衡（Nash Equilibrium，NE））［10］：在这种状态下，考虑到其他参与者采用的策略，任何参与者都不打算改变自己的策略。如果策略是ξ的NE，对于所有满足ai∈Λi和，∀i∈τ，那么设ξ是一个策略形式的博弈。

定义3（精确势博弈）［11］。战略形式博弈Ψ是一种具有势函数φ：Λ →R的精确势博弈，如果对于每个i∈τ，满足a-i∈Λ-i且可以得到：

这里将覆盖漏洞问题描述为一个潜在的多人重复博弈，在该博弈过程中，传感器节点代表参与者彼此之间可以通信，从而弥补覆盖差距。

2.3 Q学习

Q学习是一种基于马尔可夫决策过程（Markov Decision Pro‐cess，MDP）的强化学习算法，主要依赖于代理与环境之间的迭代交互［11］。在Q学习中，代理选择从当前状态st在时刻t执行动作，该动作会获得新状态st+1并提供奖励rt。因此，它包括学习根据当前状态获得的先前经验而执行的动作。策略pi(s)是代理选择每个可能状态的计划，由于学习系统和环境之间的相互作用，参与者策略逐渐得到改进。然而，在实践中，并不直接使用强化学习算法；更倾向于使用迭代求近似值函数Q(s，a)。因此，将Q(s，a)定义为未来估计收益，一旦学习到这些值，最佳策略就是选择对应于最大Q值的动作。

对于单个参与者系统，状态的效用计算为该状态关于所有可能动作的最大Q值。然而，对于多参与者系统，取决于其他参与者的联合动作，所以最优性准则不能只考虑个体的动作。因此，将Q学习扩展到多参与者框架时，应考虑其他参与者在选择动作时的行为。

事实上，Q学习算法在离散状态和动作下的性能良好［12］。然而，在现实应用中，通常是连续的空间，具有无限的状态和动作组合。Q学习不能直接适用于连续变量，空间通常需要使用近似函数进行离散化，如梯度下降、特征的线性组合和神经网络。

3 混合恢复算法

3.1 覆盖问题表达式

基于上述问题，参与者是传感器节点，可以彼此同时互相通信，以最小的功耗增强自己的覆盖区域。此外，这里假设所有参与者都是理性的，每个参与者都试图根据其对网络的局部期望和自己对其他参与者可能采取的行动的预测来增加其预期效用函数。在每个时间步长t＞0时的动作集，节点i∈τ可以选择其可能作用的集合ai∈Λi。如上文所述，混合拓扑控制使用节点重新定位和功率传输调整。因此，每个移动传感器i∈τ可以选择改变其位置pi和功率传输（传感器感应范围r）i的组合动作：ai=(pi，ri)，∀ai∈Λi。（1）假设pi=(pxi，pyi)是节点i在二维空间中的当前位置：pi→p'i是其位置的变化，其中是节点i的下一个位置。（2）假设分别是节点i的当前和下一次时间感应范围，ri→r'表示传感器感应范围的变化，Rmin和Rmax分别是传感器节点的最小和最大传感范围。效用函数每个节点i都有一个效用函数或收益函数υi：Λ →R，定义为：

式中：P(ai，a-1)、C(ai)—节点i所选择的策略的利润和成本；μα、μβ—平衡博弈利润和成本的权重。

在一个重复的博弈过程中，每个时间t参与者同时选择他们的行动策略，并接收他们的效用函数，该效用函数取决于应有的回报和付出。当所有参与者正确预测对方参与者的策略并对他们的预测做出最佳反应时，得到的结果就是纳什均衡状态。

每个节点都有一个非重叠传感区域（Non-Overlapping Sens‐ing Area，NOSA），定义为仅由相关节点覆盖的区域，如图3所示。为了使总覆盖面积最大化，缩小覆盖间隙，传感器节点应减少与相邻节点的重叠区域；因此，将利润函数最大化等同于NOSA值最大化：

式中：Ni—节点i的邻域的集合，花销成本表示恢复覆盖漏洞时传感器节点消耗的能量。

该成本主要包括两种类型：

（1）改变用Epow表示的传感器工作时功率消耗的能量：

（2）运动时消耗的能量，从而改变由Emot表示的位置。与改变节点i的感应功率相关的能量的表达式如下：

与节点运动相关的能量的表达式为：

式中：Rsi—感应范围；t—持续时间或跨度。

考虑到传感器运动和感应功率变化，总消耗能量Etot为消耗能量之和：

引理1：指定的覆盖博弈ξcov是一个精确势博弈，如果存在一个函数φ：Λ →R，从而满足∀ai，-i∈Λi，∀a-i∈Λ-i，那么有：

φ的定义式如下：

式中：Ptot—网络总覆盖率；C—传感器节点能耗。

证明。对于任何一个策略a：(ai，a-i)∈Λ，∀i∈τ，这里从Λ中任意选择一个策略：=(，a-i)。将覆盖博弈算法ξconv定义为精确势博弈。为了证明这一点，将节点i的策略从ai改为，并不改变其他策略。

可以得到：

通常，由于节点i重叠覆盖区域至少已经被另一个传感器节点覆盖，所以其任何变化都不会对整个网络覆盖产生任何影响：

因此，可以得到：

因此，当参与者i从策略ai转换到策略ddotai时，潜在函数的变化等于回报/效用函数的变化。通过参考定义3，可以证明覆盖率博弈是一个精确势博弈。

3.2 基于分布式收益的Q学习算法

收益函数不仅取决于传感器节点动作，还取决于其邻域的动作。由于分布式学习方法只需要从前面的步骤中获得回报，因此是最合适的解决方案，参与者调整自己的行为以适应其他参与者行为的变化。这里提出了一种新的基于分布式收益的Q学习算法来执行先前制定的覆盖博弈，处理的是多个参与者的博弈；因此，采用了多智能体强化学习的概念。这里所提出的算法流程如算法1所示。

算法1：基于分布式收益的Q学习算法

（1）初始化：在t=1时，所有传感器节点保持其初始随机位置。随机初始化Q(s，ai，a-i)，NbC(s，a-i)←0和n(s)←0，其中∀s∈S；∀ai∈Λi；∀a-i∈Λ-i。令α∈[ 0，1 ]作为初始学习率，ε为初始探索率。

（2）选择动作并更新状态：每次t≥2时，每个传感器节点根据以下规则更新其状态：

（3）观察电流s：n(s)←n(s)+1

（4）选择探索速率ε

（5）概率ε返回随机动作

（6）否则，概率为(1 -ε)。通过求解：

（7）学习：观察对方的行为a-i、奖励R(s，ai)和下一个状态：

（8）重复：传感器i重复执行步骤（2）、步骤（3），直到满足结束条件。

回报函数在探索和利用过程之间切换，以找到最佳的行动序列。事实上，探索过程有助于节点快速发现未知环境，而开发过程则使节点能够保持有效场景，指标ε控制系统先前获得的信息的利用与环境探索之间的权衡。

4 仿真结果分析

4.1 仿真参数设置

在模拟过程中考虑了一个正方形区域δ，其边长为100m，将其划分为预定义数量的小正方形。每个小正方形的面积为1m2，其中心是要覆盖的点，用Matlab进行了仿真试验。节点通过均匀分布随机部署在感兴趣的领域（AoI）δ中。传输范围固定为30m，传感范围在7m和15m之间随机选择，如表1所示。如果通信半径大于传感半径的两倍，则假定网络连接已满。

表1 模拟参数值设置Tab.1 Analog Parameter Value Setting

如上所述，Q学习不适用于连续空间，需要一个近似函数来离散该空间，这里使用了一种简单的离散化形式。事实上，代理执行两个操作，即更改位置和功率传输。对于每个算法迭代，节点通过沿左、右、上或下的方向移动一步来更改其位置。传感器感应半径在该集合中取一个值：7、9、11、13或15。文献［13］提出的分布式混合覆盖漏洞恢复方法缩写为DHCHRA。

算法中使用ε来平衡探索和勘探过程。使用表中给出的取值范围有助于Q学习算法收敛到最优解。

在这里，考虑了传感器移动所消耗的能量及其传感范围的变化，因此传感器应该提高其传感范围，以避免不必要的移动，尤其是在频繁出现覆盖漏洞的情况下。针对每个场景生成了四个不同大小的破坏事件。在每个新出现的覆盖漏洞之后，算法保持活动状态，直到达到95%的总覆盖率。如果未满足此阈值，则当迭代次数达到500次时，算法将停止运行。最大迭代次数设为500次，以防止传感器节点因电池中剩余能量耗尽而集体失效。

4.2 仿真结果

4.2.1 无障碍情景下的AoI

将这里的算法结果与DSSA和DHCHRA的结果进行了比较，使用四种不同的场景在相同的初始节点分布上测试了所有算法的实例。

在该场景中，呈现了一个无物理障碍的检测区域，并生成了四个破坏事件。破坏事件时间序列为1s、14s、57s和161s。一个时间样本结果，如图1所示。证明了所提出的基于博弈论的Q学习算法恢复覆盖漏洞的能力，图中的颜色是指可以覆盖区域的传感器数量。准确地说，随着颜色变为蓝色，区域中的传感器数量减少；而当颜色变为红色时，传感器数量增加。

图1 时间样本结果Fig.1 Time Sample Results

然而，一种色表示区域未被任何传感器节点覆盖。从图1（b）、图1（d）、图1（f）和图1（h）可以发现，由于连续破坏性事件而出现的新覆盖漏洞，图1（c）、图1（e）、图1（g）和图1（j）说明了处理四个覆盖漏洞的势博弈行为。这些结果图清楚地显示了这里拓扑控制方案在连续覆盖漏洞后，修复网络并保持最高覆盖阈值的效率。传感器节点调整传感范围和位置，以便快速准确地弥补覆盖范围的差距。

给定算法中出现每个覆盖漏洞NS=250个节点后所需迭代次数的平均值，如图2所示。对于这三种算法，迭代次数随着连续事件的出现而增加。DSSA和DHCHRA分别在事件2和事件3后达到停止标准，迭代次数等于500。与其他方法相比，该方法收敛速度更快。它成功地恢复了四个覆盖漏洞，并在达到停止标准之前达到上述覆盖阈值，即总覆盖面积的95%。

图2 迭代次数的平均值Fig.2 Average Number of Iterations

DHCHRA、DSSA的总覆盖率的百分比，以及考虑到AoI中部署的传感器节点（50到250个节点）的数量，总覆盖率性能对比，如图3所示。在连续四个覆盖漏洞出现期间，对总覆盖率进行评估。从图3中可以看出，所提出的算法在整体网络覆盖方面优于上述算法，并模拟了DSSA、DHCHRA 和提出的方法在能耗方面的效率。

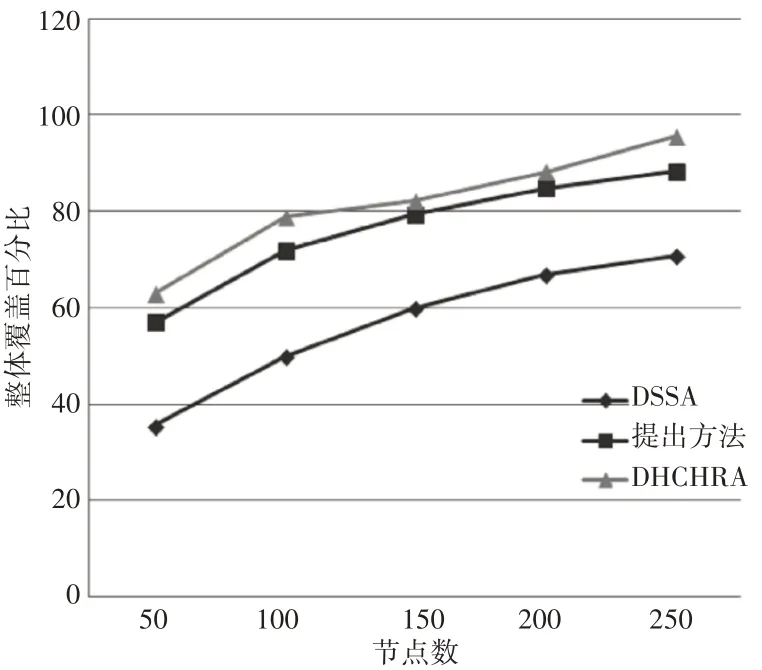
图3 总覆盖率性能对比Fig.3 Comparison of Total Coverage Performance

与感测功率的变化相关的消耗能量、与节点运动相关的消耗能量以及总消耗能量，如图4（a）～图4（c）所示。结果表明，这里的方法在能耗方面优于其他两种方法。如图2 所示，与DSSA 和DHCHRA 相比，所提出的方法对连续覆盖漏洞具有快速响应。这些结果意味着传感器节点在覆盖范围方面移动占据其最佳位置的可能性较小，这使网络能够消耗较少的能量，如图4 所示。从而能够扩展网络的生存能力。

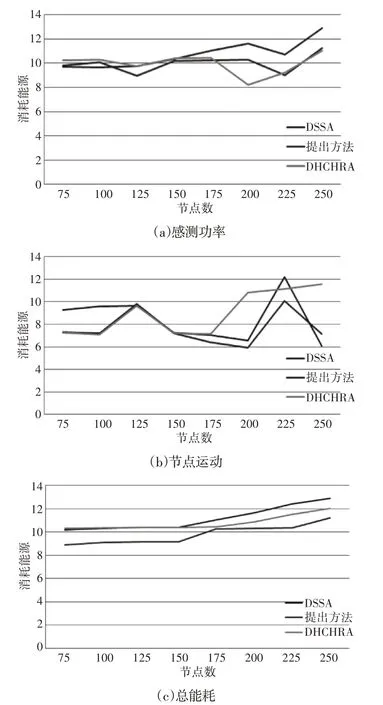
图4 三种情况下的能量消耗Fig.4 Energy Consumption in Three Cases

4.2.2 有障碍情景下的AoI

为了使这里模拟更接近实际情况，我们在模拟场景中考虑了两种障碍物形状：矩形和T形，将障碍物放在AoI的中心，传感器节点可以放置在障碍物的边界上。这两种情况的结果如下，一个时间段的示例，证明了所提出的基于博弈论的Q学习算法能够分别恢复包含矩形和T形障碍物的检测区域中的覆盖漏洞，如图5、图6所示。

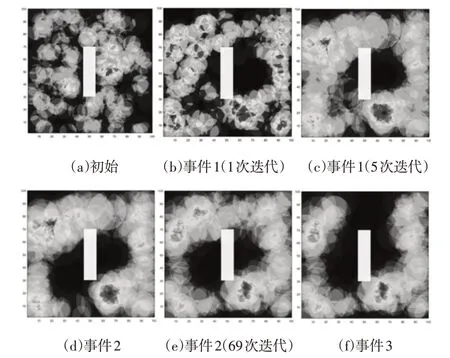
图5 矩形时间样本事例Fig.5 Time Sample Examples of Rectangle

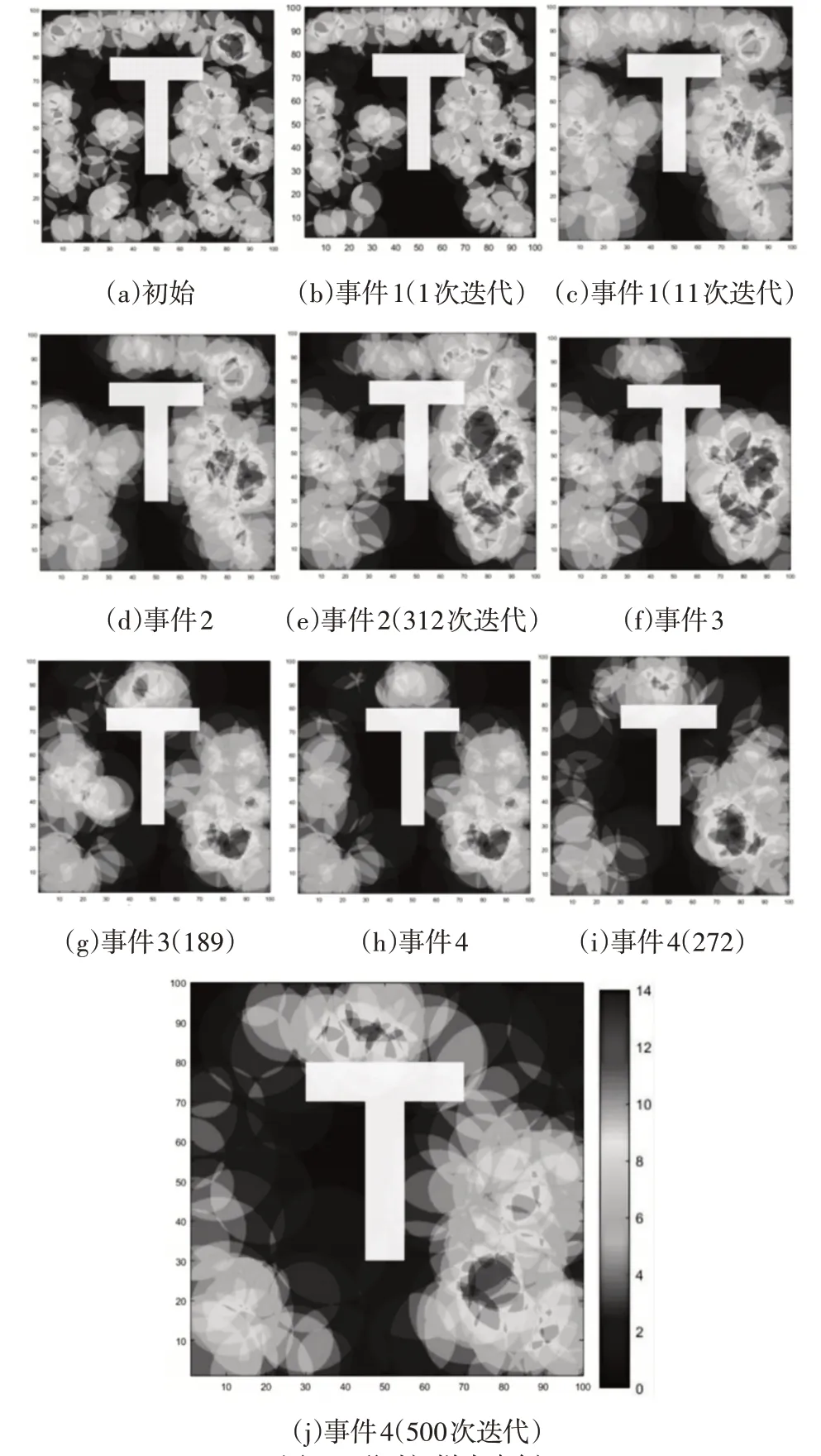
图6 T形时间样本事例Fig.6 Time Sample Examples of T

矩形障碍场景和T形障碍场景中由于连续破坏性事件而出现的新覆盖漏洞，如图5（b）、图5（d）、图5（f）、图5（h）和图6（b）、图6（d）、图6（f）、图6（h）。矩形障碍情景和T形障碍情景的破坏事件时间序列分别为1s、5s、70s和273s，以及1s、11s、169s和312s。其他子图说明了处理矩形障碍物形状检测区域中四个覆盖漏洞的方法的行为。图中结果证明了这里的方法即使存在障碍物的情况下仍旧具备消除覆盖漏洞的能力。

针对所提出的障碍场景恢复每个覆盖漏洞所需的迭代次数的平均值，如图7所示。对于矩形障碍物场景，DSSA和DHCHRA在事件2后达到停止标准。这里的方法恢复了四个覆盖漏洞，在达到停止标准之前成功地达到了覆盖阈值。对于T形障碍场景，DSSA 和DHCHRA 分别在事件1 和事件2 后达到停止标准。然而，这里的方法在达到总覆盖面积的92%之前恢复了四个覆盖漏洞。

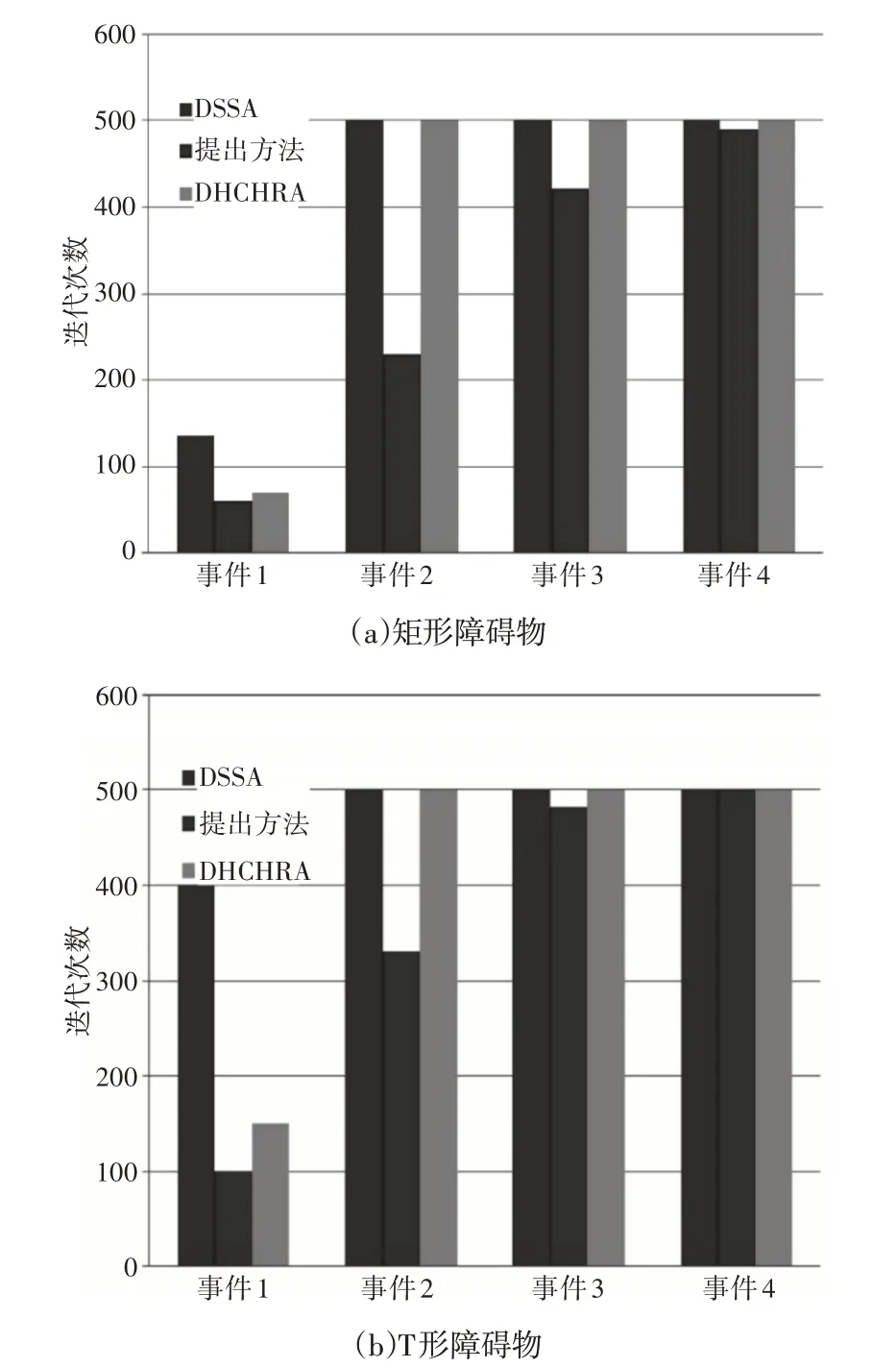
图7 迭代次数的平均值Fig.7 Average Number of Iterations

DHCHRA、DSSA 的总覆盖率的百分比，以及这里的算法改变部署在具有障碍物的检测区域中的传感器节点的数量如图8所示。在连续四个覆盖漏洞出现期间，对总覆盖率进行评估。从图中可以发现，即使在存在障碍的情况下，提出的算法在总体网络覆盖率方面也优于其他算法。

图8 覆盖率情况Fig.8 Overall Coverage

DSSA、DHCHRA 的效率，以及这里的算法在有障碍物的探测区域消耗的能量，如图9、图10所示。与感测功率变化相关的消耗能量、与节点运动相关的消耗能量和总消耗能量，如图9（a）、图9（b）、图9（c）、图10（a）、图10（b）、图10（c）所示。结果表明，这里的方法在能耗方面优于两种方法。

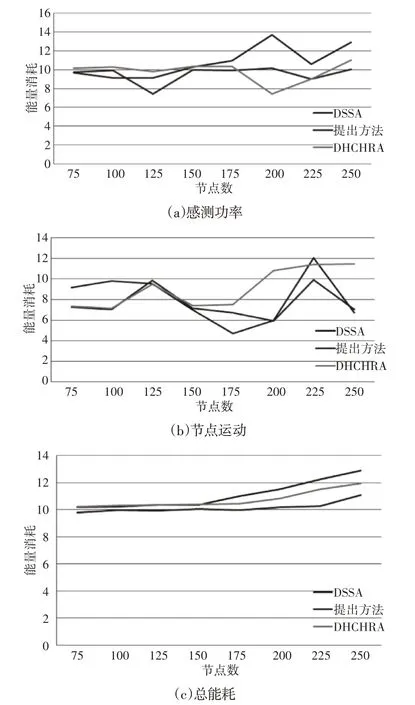
图9 矩形障碍下的能量消耗Fig.9 Energy Consumption Under Rectangular Obstacles

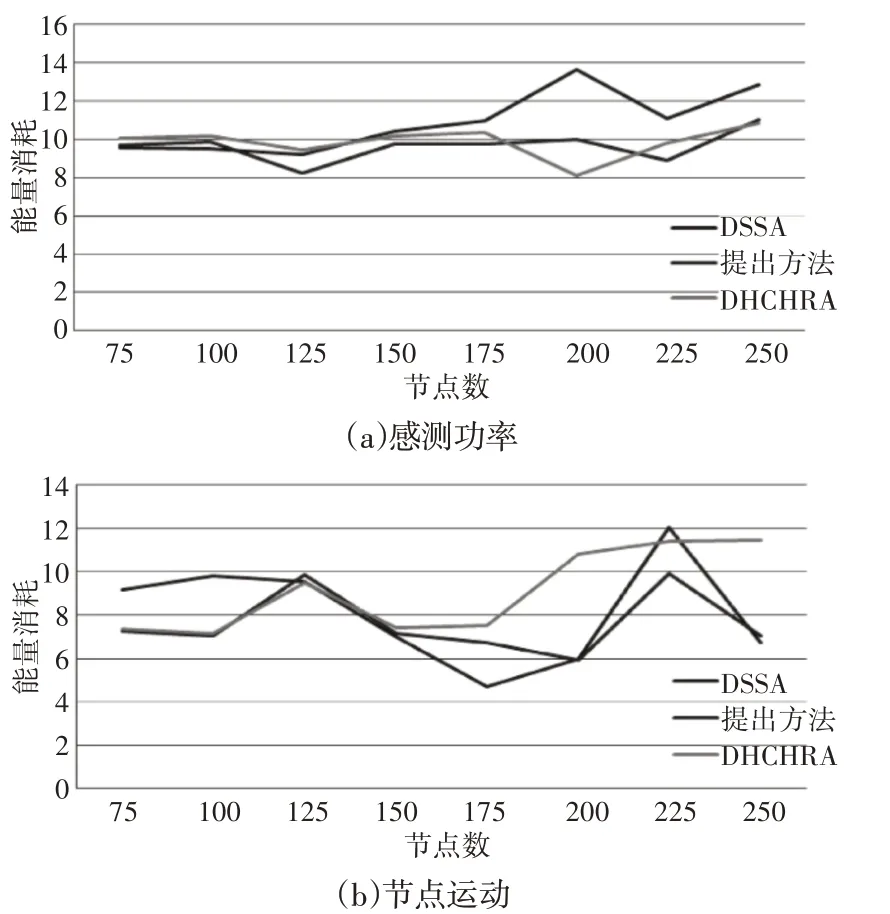
图10 T形障碍下的能量消耗Fig.10 Energy Consumption Under T Obstacles

4.2.3 无需功率调整的拓扑控制方案

许多无线传感器网络应用不支持功率传输调整，因此，在本节中，提出了一种在无障碍AoI中测试的无功率控制拓扑控制策略，节点的动作仅限于位置调整。针对不同建议场景，即无障碍AoI、矩形障碍AoI、T形障碍AoI以及无障碍AoI无功率调整的控制拓扑方案，这里的方法的总覆盖面积的百分比，如图11所示。通过改变传感器节点的数量（从50到250个节点），评估总覆盖率的百分比。从图11可以发现，对于每个提出的场景，即50、100、150和200个节点，这里的方法均获得了令人满意的覆盖率。此外，有250个节点达到了覆盖阈值（总覆盖面积的95%），但T形障碍场景仅达到总覆盖面积的93%。这里的方法在所有场景中的能耗结果，如图12所示。对于无障碍场景、矩形障碍场景和T形障碍场景，能耗值均是收敛的。然而，在不进行功率调整的情况下，该方法的能耗明显增加。

图11 这里方法的总覆盖百分比Fig.11 Total Coverage Percentage of Proposed Method

图12 能耗结果Fig.12 Energy Consumption Results

5 结论

针对恶劣环境下分布式无线传感器网络，为了降低成本与恢复能力，提出了一种Q学习博弈论的无线传感器网络混合覆盖漏洞恢复方法。最后仿真结果可以证明如下结论：

（1）提出的方法有助于传感器有效预测应采取的最佳策略，并执行最准确、最成功的决策，从而能够在实现恶劣环境下分布式无线传感器网络的覆盖漏洞恢复，并且能够降低能耗成本。

（2）与其他算法相比，在无功率调整的情况下，该算法的覆盖率是收敛的，然而，能耗有所上升。

（3）在无障碍AoI场景和有障碍AoI场景中，这里的方法所产生的拓扑控制方案在能耗和覆盖率方面优于其他方法。但是，在有障碍物的情况下，在遵守预定义的覆盖阈值的同时恢复覆盖漏洞的方法的降低了恢复速度。