Mechanical property of cylindrical sandwich shell with gradient core of entangled wire mesh

Xin Xue , Cho Zheng , Fu-qing Li ,*, Xue-qin Wu ,b,**

a Institute of Metal-rubber & Vibration Noise, School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, 350116, China

b Fujian Metallurgical Industry Design Institute, Fuzhou, 350116, China

Keywords: Entangled wire mesh Gradient cylindrical sandwich shell Vacuum brazing Secant stiffness Damping

ABSTRACT To explore the wide-frequency damping and vibration-attenuation performances in the application of aerospace components, the cylindrical sandwich shell structure with a gradient core of entangled wire mesh was proposed in this paper.Firstly, the gradient cores of entangled wire mesh in the axial and radial directions were prepared by using an in-house Numerical Control weaving machine, and the metallurgical connection between skin sheets and the gradient core was performed using vacuum brazing.Secondly, to investigate the mechanical properties of cylindrical sandwich shells with axial or radial gradient cores, quasi-static and dynamic mechanical experiments were carried out.The primary evaluations of mechanical properties include secant stiffness, natural frequency, Specific Energy Absorption(SEA),vibration acceleration level,and so on.The results suggest that the vibration-attenuation performance of the sandwich shell is remarkable when the high-density core layer is at the end of the shell or abuts the inner skin.The axial gradient material has almost no influence on the vibration frequencies of the shell, whereas the vibration frequencies increase dramatically when the high-density core layer approaches the skin.Moreover, compared to the conventional sandwich shells, the proposed functional grading cylindrical sandwich shell exhibits more potential in mass reduction, stiffness designing, and energy dissipation.

1.Introduction

A functional gradient (FG) cylindrical shell is a new type of structure.Its material distribution exhibits a continuous gradient change along a certain direction [1,2].Gradient structure demonstrates excellent mechanical properties under concentrated load as well as non-uniform load[3-5].Being a porous elastic material,the entangled wire mesh has wide application prospects, such as aviation, rail transit, and submarine.It has the structural characteristics of nonlinearity, high elasticity, multi-porosity, high-temperature resistance, and anisotropy when compared with conventional metal foams [6,7].Its structure can overcome the performance mismatch between different structural materials of the traditional functional gradient.Therefore, the entangled wire mesh is a functional gradient structure.These functionally graded cylindrical shells can optimize the structural bearing capacity and reduce the mass.Its continuous gradient variation characteristics can effectively alleviate the phenomenon of interlaminar stress concentration [8,9].Xiao et al.[10] used gradient metal porous materials to replace the conventional uniform porous core.The effects of three gradient cores(unidirectional distribution,positive gradient symmetrical distribution, and negative gradient symmetrical distribution) on the natural frequency of sandwich skins are analyzed.The gradient distribution of the core and the thickness of the skin has a crucial impact on the dynamic response and failure mode of the structure [11].Zhang et al.[12] combined the characteristics of functional gradient and honeycomb sandwich structure to prepare the gradient honeycomb sandwich plate.They analyzed the stability of the sample.The results indicate that there is a nonlinear relationship between the thickness of the honeycomb skin and the deviation of the normalized buckling load factor.Song et al.[13] prepared a layered composite structure with TiB_2/42CrMo by the centrifugal reaction casting process.The ceramic/alloy phases in the interlayer illustrate continuous gradient evolution on the spatial scale.The material has the characteristics of interlaminar shear strength and failure delay behavior of metal-like materials.Liu et al.[14] designed the Hierarchical Thermoplastic Composite Honeycomb Graded Structures (HTCHGS) using continuous woven glass fiber.The structure enhances the deformation stability and makes the failure process predictable.Zhang et al.[15]observed that the energy absorption capacity of uniform foam metal under low-speed loading is higher than that of the gradient foam metal structure.Under high-speed loading, the gradient foam metal exhibits a higher energy absorption ratio in the early stage of compression along the negative gradient direction.Gohari et al.[16] studied the working performance of piezoelectric chips in variable temperature environment, and included the uncertainty into the formula for the first time.Accordingly,the designed controller not only should be robust against these uncertainties but also should have a desirable performance.Moreover,Zarastvand et al.[17] proposed a strategy that can be applied to predict the acoustic features of the stiffened systems to achieve better sound insulation for the stiffened doubly curved shells.Many scholars have described and predicted the mechanical properties of functionally graded cylindrical shells by establishing certain theoretical models.Based on the First-order Shear Deformation Theory(FSDT),Yang et al.[18]described the composite laminate layer and viscoelastic material layer,respectively,by using lamination theory and sandwich theory.They came up with an accurate solution for the free vibration and damping analysis of a thick cylindrical sandwich shell with a viscoelastic core under arbitrary boundary conditions.Shahgholian et al.[19,20]performed buckling analyses of functionally graded porous nanocomposite cylindrical shells reinforced with graphene platelets (FGPNCS-R-GPLs) under uniform external lateral pressure.The theoretical governing formulations are derived, and then they are solved using Rayleigh-Ritz method to obtain the critical buckling pressure.Moreover, Shahgholian et al.[21] investigated torsional buckling analysis of functionally graded graphene-platelets reinforced composite (FGGPLRC) porous cylindrical shell.First-order shear deformation theory and Rayleigh-Ritz method are employed to establish the related eigenvalue equations in order to calculate the critical buckling torque.Based on the von K'arm'an nonlinear plate theory,Chen et al.[22-24] used the Hamilton principle to derive the coupled nonlinear partial differential equation controlling the inplane displacement and transverse displacement of the BDFG plate.This can further influence the variation of gradient parameters and geometric defects on the nonlinearity of resonance response.Based on Flügge's theory, Chen et al.[25] deduced the dynamic differential equation of the FGM cylindrical shell under elastic boundary conditions.They used the improved Fourier series method to solve the natural frequency of the FGM cylindrical shell.The effects of shell size and volume fraction on the vibration characteristics are analyzed.Based on the love shell theory,Li et al.[26] analyzed the vibration characteristics of the FGM cylindrical shell under the energy principle of rotating cylindrical shell and the Rayleigh-Ritz method.Based on the Pasternak-type Elastic Foundation(PEF),Zarastvand et al.[27]proposed a strategy on modeling poroelastic doubly curved composite shells.The results represent the effect of modeling poroelastic doubly curved composite shells subjected to a PEF on acoustic characteristics regarding each of Winkler spring and shear layer stiffness.

The key research content is the preparation and mechanical properties of the gradient cylindrical sandwich shell with entangled wire mesh (axial and radial gradient distribution).The manufacturing and brazing technology of the gradient cylindrical sandwich shell with entangled wire mesh is proposed in this paper.The quasi-static compression, sinusoidal sweep vibration test, and sinusoidal fixed vibration test are carried out.The static and dynamic mechanical characteristics are measured.Further, the static and dynamic mechanical characteristics and damping energy dissipation mechanism of the gradient cylindrical sandwich shell with entangled wire mesh are described.The test results are explained from the micro/macro points of view.

2.Material preparation

Entangled wire mesh is an elastic porous damping material.It is prepared by the technological process chain of wire feeding,stretching, twining, winding, stamping, and post-treatment [28].The preparation process of the gradient cylindrical sandwich shell with entangled wire mesh is demonstrated in Fig.1.The material of the wire, the diameter of the wire, and the diameter of the spiral coil are designed.The mechanical properties of the spiral coil tend to change in all aspects (see Fig.2).

2.1.Preparation of the entangled wire mesh

The material selection of the metal wire is dependent on the service environments and the requested performances of the entangled wire mesh.In this work,the raw material is nickel-based superalloy wire (Graded GH4169), which is an important material for high temperature structure components in the field of aerospace.Table 1 shows the mechanical property parameters of the used GH4169.

The preparation of entangled wire mesh mainly can be summarized as the following four processes:(i)Encircling the selected metal wire into a tight helix by a specific in-house twist-distortion machine.(ii)Stretching the tight helix into a fixed pitch(3 mm)by providing a suitable pre-tension, and forming a coil wire.(iii)Entangling the coil wire in a crisscross pattern into a rough porous blank.(iv)Applying a compressive force for the rough porous base material by using a desired shaping tool to obtain a tight and entangled wire mesh.(v) Post-treatment (cleaning and heat treatment) of tight and entangled wire mesh.

It should be noted that their there are slight impurities and dust particles in the cavity inner the entangled wire mesh.The source is mainly from the fabrication process and dry friction induced wear of interwoven wires.In the stamping stage of fabrication process,the blank of entangled wire mesh undergoes severe plastic deformation and contact friction.This can lead to generate a slight impurities and dust particles in the entangled wire mesh.Therefore,the sample should be ultrasonic cleaning before brazing.

2.2.Brazing process

The skins were made of GH4169 sheet with a thickness of 0.2 mm.The metallurgical connection between skin sheets and the gradient core was performed using vacuum brazing [28,29].This process can realize the metallurgical solid phase bonding at the interface.Moreover,the process can ensure the effectiveness of the face core connection.The brazing fixture and tooling are designed to clamp the welding object into the high-temperature furnace(GSL-1400X, Hefei Kejing Material Technology Company, Hefei,China).They are brazed according to the heating curve.

For wetting and spreading effectively on the surface of the entangled wire mesh and skin, the contact surface of the sample shall be roughened with 400 mesh sandpaper (Lay GH4169 outer skin,BNi-2 solder,entangled wire mesh,BNi-2 solder,and GH4169 inner skin).Put this in the brazing equipment and assemble it.After aligning each layer, insert and support the split mandrel.The entangled wire mesh is a porous material and has good elasticity.The entangled wire mesh with a thickness designed slightly more than 5 mm is preloaded to 5 mm by locking the bolts on both sides of the brazing equipment.This ensures the effectiveness of the contact between the core and the skin in the brazing process.To weaken the effect of high temperature during brazing, 310 S bolts are selected.The brazing equipment is designed as a split structure,as demonstrated in Fig.3(a).

Fig.1.Preparation process of gradient cylindrical sandwich shell with entangled wire mesh.

Fig.2.Preparation process of the entangled wire mesh: (a) GH4169; (b) Metal spiral coil; (c) Winding blank; (d) The entangled wire mesh.

Table 1GH4169 Mechanical property parameters at room temperature.

The assembled brazing equipment is then put into the hightemperature furnace (GSL-1400X, Hefei Kejing Material Technology Company, Hefei, China), as shown in Fig.3(b).The molecular pump starts to extract the air in the furnace to a vacuum of 2.5×10-3Pa.It is known that the liquidus of BNi-2 is 1010°C,and the solidus is 970°C.The heating rate must be well-controlled to ensure that the brazing object is fully and evenly heated in the brazing process,as shown in Fig.3(c)[28].Firstly,the temperature in the furnace is controlled to rise at the rate of 5°C/min until it reaches 950°C.Secondly, heat is preserved for 30 min.Thirdly,the temperature is raised at the rate of 5°C/min until 1050°C.Fourthly,heat preservation is done for 20 min.Eventually, the furnace is cooled to 500°C.This method ensures that the solder is filled and distributed between the entangled wire mesh and the GH4169 skin.The sample can be taken out of the furnace after naturally cooling it to the normal temperature.

2.3.The gradient cylindrical sandwich shell with entangled wire mesh design scheme

Fig.3.Brazing process: (a) The diagram of brazing fixture tooling; (b) Vacuum braze furnace; (c) The curve of brazing temperature.

Fig.4.Schematic diagram of sandwich skin with gradient metallic cellular core:(a)Unidirectional distribution;(b)Positive gradient symmetrical distribution;(c)Negative gradient symmetrical distribution.

In order to better demonstrate our design scheme, Fig.4 illustrates three typical gradient distribution of the core layer, i.e.,unidirectional distribution, positive and negative gradient symmetrical distributions.The gradient distribution of the core layer can be achieved by means of the different density of sub-layer.

The gradient distribution schemes of the core density along the axial and radial directions are proposed as follows:

(1) Axial gradient distribution: Designing of four axial gradient density distribution schemes of the core is done.The core is divided into three layers from top to bottom along the axis(as explained in Fig.5), and the width of each layer is 20 mm.The gradient distribution schemes are enlisted in Table 2.Considering sample-A as an example,the density of the first layer is 2.0 g/cm3,and the density of the second and third layers is 1.0 g/cm3.

(2) Radial gradient distribution: Four radial gradient density distribution schemes of the core are designed, which are divided into three layers: 0-0.15 mm, 0.15-0.35 mm, and 0.35-0.5 mm along the radial direction, as illustrated in Fig.6.These four schemes are enlisted in Table 3.Taking sample E as an example,the density of the first layer is 2.25 g/cm3,and the density of the second and third layers is 1.0 g/cm3.Sample H is a uniform distribution layer that is used for comparison.

The simple gradient cylindrical sandwich shell with entangled wire mesh size is shown in Fig.7 and Table 4.

3.Experimental procedures

3.1.Static mechanical test

As a gradient structure, the loading form and displacement of each stage may have a significant influence on it.The damping characteristics of the axial and radial gradient cylindrical sandwich shell with entangled wire mesh under quasi-static loading and unloading are observed.The test method includes placing the gradient cylindrical sandwich shell with entangled wire mesh sample horizontally on the test platform of the universal testing machine(WDW-T200,China Jinan Tianchen Machine Manufacture Company, Jinan, China), as Fig.8.The test sample is loaded after placing it horizontally.The loading displacement is controlled at 2 mm.The measuring range of the force sensor is 1000 N.The force loading rate is 0.5 mm/min.

Fig.5.Axial gradient entangled wire mesh damping layer.

Table 2The axial gradient distribution scheme of core density.

In the process of quasi-static loading,the static restoring forcedisplacement curve of the gradient cylindrical sandwich shell with entangled wire mesh is shown in Fig.9.The area covered by the curve represents the static damping energy dissipation ΔWs.The triangular area enclosed by the point, abscissa, and coordinate origin at the maximum loading displacement and the corresponding static restoring force in the figure represents the static maximum elastic potential energyWs.The slope of the hypotenuse of the triangle represents the secant stiffness.In addition, specific energy absorption (SEA) is used to evaluate the energy absorption effect of damping material per unit mass.The calculation formula is

Table 3The radial gradient distribution scheme of core density.

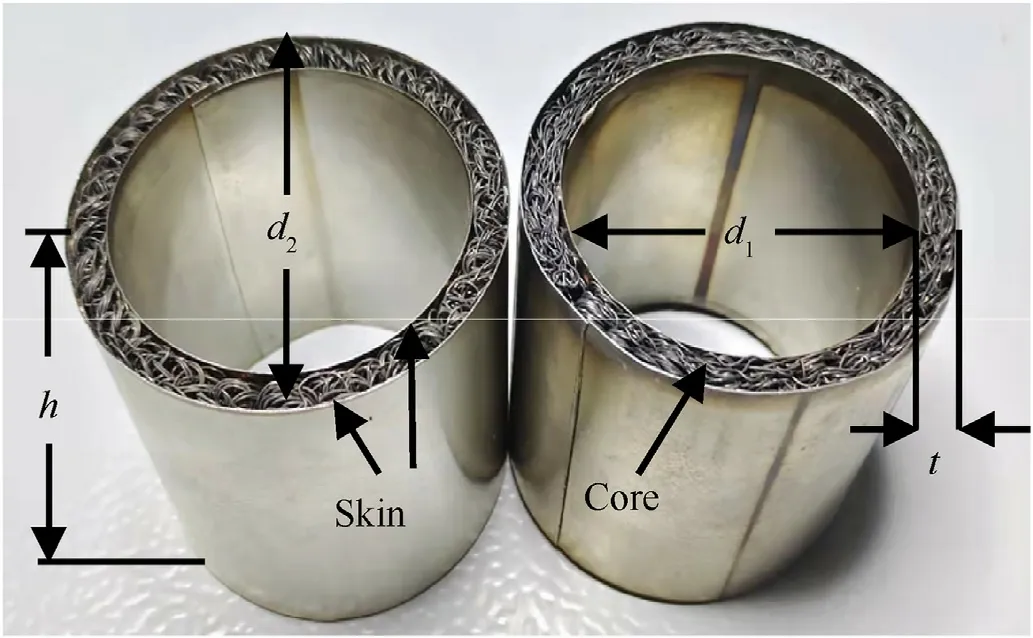
Fig.7.The simple gradient cylindrical sandwich shell with entangled wire mesh.

Table 4The size of the gradient cylindrical sandwich shell with entangled wire mesh.

Fig.8.Quasi-static loading and unloading test platform.

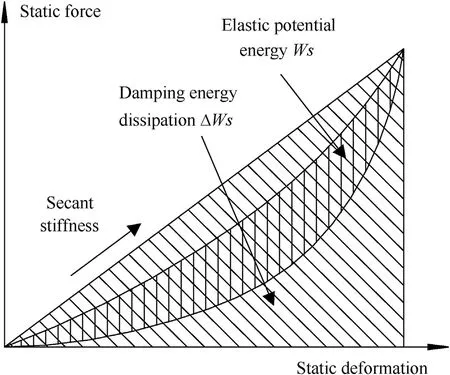
Fig.9.Static restoring the force-displacement curve.

3.2.Dynamic mechanical test

To test the dynamic performance of the gradient cylindrical sandwich shell with entangled wire mesh, the test sample is excited.The excitation signal and acceleration response signals are collected by the DH5922 N dynamic test system.The frequency response curves of the test object are obtained through postprocessing using the modal analysis software.The experimental equipment and system for dynamic mechanics of cylindrical sandwich shell is shown in Fig.10.

As demonstrated in Fig.11, the cylindrical sandwich shell with entangled wire mesh is cantilevered on the test platform with a customized fixed flange.One end of the cylinder has fixed support,and the other end is free.The acceleration sensor is arranged at the free end.The skin of the cylindrical sandwich shell with entangled wire mesh is thin,and the overall stiffness is low.An exciter is used to excite it at 5 N.

The basic flow of sinusoidal sweep is as follows: output sinusoidal signal to the power amplifier through a signal generator.To drive the vibration exciter, the power amplifier amplifies the sinusoidal signal.The output power of the power amplifier is adjusted according to the force signal measured by the force sensor.The exciting force is controlled to 5 N.The force sensor and acceleration sensor receive the force signal and acceleration signal on the surface of the cylindrical sandwich shell.It is collected using a data collector.The acquisition frequency band is 5-2000 Hz.The excitation point and signal pickup point are illustrated in Fig.11.

As shown in Fig.12, the stress-strain curve of the gradient cylindrical sandwich shell with entangled wire mesh after being loaded and unloaded by a simple harmonic cycle is shown.It can be seen from the figure that the loading curve is above the unloading curve, indicating that the force corresponding to loading and unloading under the same displacement is different.The curve is annular as a whole.The area covered by the annular curve corresponds to the energy consumed by the test sample before and after deformation, It can be seen that the gradient cylindrical sandwich shell with entangled wire mesh retains the nonlinear hysteresis characteristics of entangled wire mesh.The area covered by the curve in the figure represents the energy dissipated by the gradient cylindrical sandwich shell with entangled wire mesh in a single cycle during the cycle andWis the maximum elastic potential energy stored in the cycle.When the dynamic stiffnessKdis calculated by using the elliptic method,which can be expressed as

In addition, the index of vibration acceleration level is introduced to evaluate the response of surface acceleration when the research object is excited.The vibration acceleration level reflects the severity of the vibration.The calculation formula for vibration acceleration level is

whereaeis the effective value of the acceleration signal measured on the surface of the gradient cylindrical sandwich shell with entangled wire mesh, andaois the reference acceleration.According to the Code for Design of Environmental Protection in the Machinery Industry, the reference acceleration is taken as 1 × 10-6m/s2.

4.Results and discussion

4.1.Effect of gradient core on static characteristics

The deformation of inner and outer skins is different when the gradient cylindrical sandwich shell with entangled wire mesh deforms under the load.Therefore, the extrusion and pulling of the sandwich layers are different.Entangled wire mesh is an elastic porous material with excellent damping characteristics.The deformation of the entangled wire mesh is accompanied by friction and extrusion of the internal metal wires.This causes energy dissipation.Research is being done to study the change in the loaddisplacement curve.

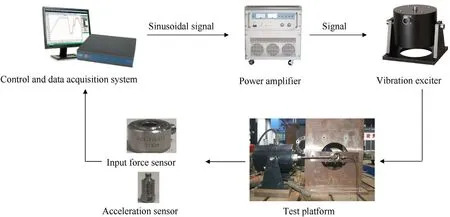
Fig.10.The experimental equipment and system for dynamic mechanics of cylindrical sandwich shell.

Fig.11.Experimental platform for dynamic mechanics of cylindrical sandwich shell.

Fig.12.Dynamic restoring the force-displacement curve.

Figs.13 and 14 show the load-displacement curves of axial and radial gradient cylindrical sandwich shells with entangled wire mesh, respectively.From the test results, it can be found that the load-displacement curve of the gradient cylindrical sandwich shell with entangled wire mesh has a certain nonlinearity.The loading curve is above the unloading curve.This suggests that the forces in the loading stage are different from those in the unloading stage under the same displacement.The energy dissipation of the test sample occurs during deformation.This phenomenon indicates that the structure reflects the damping characteristics of the entangled wire mesh material.The area covered by the loaddisplacement curve highlights the energy dissipation by the gradient cylindrical sandwich shell with entangled wire mesh under deformation.The mechanical characteristics of the gradient cylindrical sandwich shell with entangled wire mesh are nonlinear.The secant stiffness is calculated based on the load-displacement curve.

Fig.13.Load-displacement curve of axial gradient cylindrical sandwich shell with entangled wire mesh.

Table 5 highlights the changes in the secant stiffness and Specific Energy Absorption(SEA)of the test sample calculated based on the test results.For the axial gradient distribution of cylindrical sandwich structure, there are not significant change of secant stiffness with the studied gradient distributions.This is because the stiffness of cylindrical sandwich structure with entangled wire mesh core is mainly depended on the skin sheet,whose stiffness is much larger than flexible core in the axial direction.In the other words, the axial gradient distribution of the core in the sandwich structure makes few effects on the axial stiffness of the entire structure.In addition, the secant stiffness of unidirectional distribution (e.g., sample A and C) is slightly lower than that of positive or negative gradient distribution (e.g., sample B and D), and the sample B with negative axial gradient distribution has the largest secant stiffness.The relatively high core density is concentrated in the middle region in the axial direction.Generally, the entangled wire mesh in the high-density region gradually diffuses to the lowdensity region under the axial loading.This results in some metal wires arranged on the edge may overflow and then a slight degradation of axial secant stiffness.In addition, sample B has the largest SEA in the loading and unloading cycle.This is because the distribution of the stress is more concentrated in the high-density region under loading.This region plays a major role in energy absorption and dissipation.

Fig.14.Load-displacement curve of radial gradient cylindrical sandwich shell with entangled wire mesh.

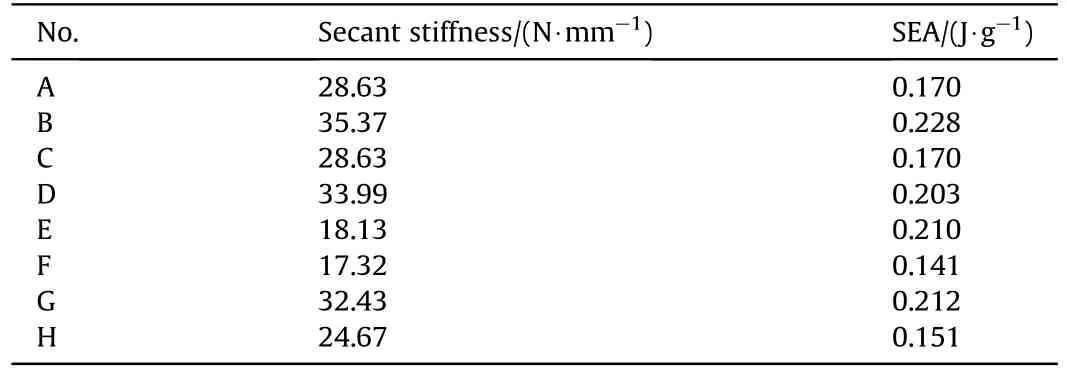
Table 5Secant stiffness and SEA of radial gradient cylindrical sandwich shell with entangled wire mesh.

For the radial gradient distribution of cylindrical sandwich structure, it can be observed that the sample G has the maximum secant stiffness.Since the outer layer with high core density in the radial direction is connected with the external skin by brazing technology, there must be more solder joints than the other core layers.The number of solder joints is directly affected the secant stiffness in the radial direction.Similarly, it can be explained that the difference of secant stiffness between sample E and F is slight due to the same density of outer layer.And their secant stiffness in the radial direction is lower than the others due to low density of the external core layer.

Additionally,there are some analytical formulations that shows the relation of between the density of entangled wire mesh and stiffness.For example, Xue et al.[30] deduced the equivalent stiffness model of metal rubber (also known as entangled wire mesh)based on the micro-spring unit.The specific analysis formula is as follows:

whereKEis the equivalent stiffness of entangled wire mesh,KSis the stiffness of the micro-spring unit along the pressure direction,and ρris density.According to Eq.(4),the stiffness of the sample of entangled wire mesh increases with the density.

Sample G has a maximum SEA.The reason is associated with the dry friction induced energy absorption.The energy transmission path under static loading is from external side to internal side.Since the amplitude is small, the external core layer makes a dominate effect on the whole energy absorptions.When the external layer of the entangled wire mesh core has a relatively high density, it can lead to a greater energy absorption due to a more contact points for dry friction.The radial gradient distribution of sample G from internal side to external side is 1.0-2.25 g/cm3.It has the greatest density of external core layer among the studied samples.

Comparing the two gradient distribution laws,it can be inferred that changing the gradient structure of the core layer of the cylindrical sandwich shell has an obvious effect on the static characteristics.The secant stiffness of the structure is positively correlated with the SEA.Thus, the following two cases can lead to better stiffness and damping characteristics under loading.

(1) In the axial gradient distribution, the core density is distributed to the middle section.

(2) In the radial distribution, the core density is distributed on the outer side.

4.2.Effect of gradient core on dynamic characteristics

4.2.1.Thesinusoidalsweepvibrationtest

The bottom of the gradient cylindrical sandwich shell is locked with entangled wire mesh on the platform.The test sample is subjected to sinusoidal sweep excitation.The excitation force is 3 N.The test frequency band is 5-2000 Hz.The change in surface response magnitude of the test sample is further measured.Figs.15 and 16 are frequency response curves obtained from the test.H(ω)stands for acceleration frequency response, andfdenotes frequency.

Tables 6 and 7 demonstrate the first fourth natural frequencies and vibration acceleration level of the test sample calculated by the frequency response curves.According to the comparison of the axial gradient distribution scheme given in Table 6, the vibrationattenuation effect of sample C is significant.According to the knowledge of material mechanics, it can be explained as follows.

The vibration-attenuation effect of Sample C is remarkable.It can be explained by two potential reasons:The first one is that the vibration acceleration response of unidirectional gradient core structure is lower than that of non-unidirectional gradient core structure due to the characteristics of dominate bending mode.In all the modes,the deformation response is the lowest in the middle part of cylindrical sandwich structure in the axial direction and the largest on both sides.The energy dissipation mechanism of the entangled wire mesh is that the deformation after loading induces the dry friction of internal wires.Therefore, the vibration acceleration level or damping energy dissipation is greater when the higher density is distributed to both sides in the axial direction(Sample A and C) than in the middle (Sample B and D).The other reason may be the excitation condition in the end side of sandwich structure in the axial direction.Due to a high density of entangled wire mesh core in the end side of sandwich structure should lead to a higher stiffness in the initial exciting position.This can be explained that the vibration attenuation effect of sample C is the lowest than the other ones due to the highest core density at the end side and the initial excitation position.The above exploration of vibration attenuation effect of cylindrical sandwich structures with different gradient cores may be not comprehensive due to not enough measured data on gradient configuration.

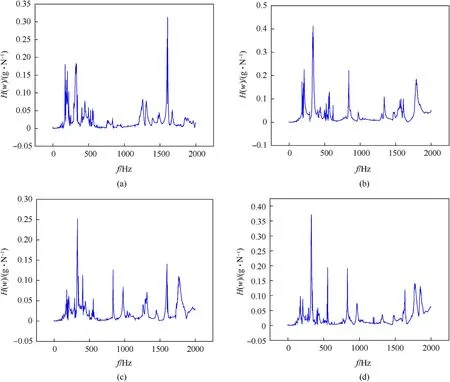
Fig.15.The frequency response curve of axial gradient cylindrical sandwich shell with entangled wire mesh: (a) Sample A; (b) Sample B; (c) Sample C; (d) Sample D.

The reasons for the result that the influence of radial gradient distribution on natural frequency is remarkable compared to axial one can be explained as follow:The proposed cylindrical sandwich shell with gradient core of entangled wire mesh is a flexible structure, which mainly occurs in the radial direction.The skin panel of cylindrical sandwich shell plays a dominant role on the stiffness and the natural frequency.It is almost a constant part in this work.In addition,it should be noted that the influence of radial gradient distribution on secant stiffness is remarkable compared to axial one has also been proved by some other similar structures.For example, Yang et al.[31] reported that increase of the stiffness of cylindrical sandwich shell will increase the natural frequency.

According to the above experimental phenomenon, it can be preliminarily inferred that.

(1) The concentration of the core density in the axial middle section will aggravate the surface response of the cylindrical sandwich shell.

(2) The distribution of the density close to the end of the shell of the cylindrical sandwich shell is beneficial to improve the vibration-damping effect of the structure.

(3) The influence of radial gradient distribution on natural frequency is remarkable compared to axial one.

It can be observed from Table 6 that the high-density part of the core tends to be distributed externally along the radial direction,which will aggravate the surface response of the cylindrical sandwich shell.As measured by sample G,the vibration effect is intense when the mass of the damping layer tends to be distributed outer the cylindrical sandwich shell.As given in the test results of sample E,the damping characteristics are best when the core density tends to be distributed inner the cylindrical sandwich shell.Comparing the core with a uniform density distribution, the damping characteristics are enhanced as the density tends to be distributed toward the innermost layer.Therefore, the mass distribution toward the inner side of the core improves the damping characteristics of the structure.

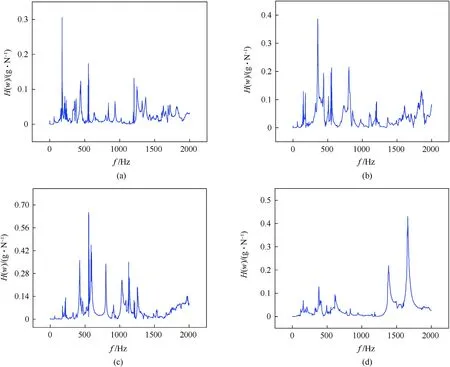
Fig.16.The frequency response curve of radial gradient cylindrical sandwich shell with entangled wire mesh: (a) Sample E; (b) Sample F; (c) Sample G; (d) Sample H.

Table 6Effect of axial gradient sandwich on acceleration response of the cylindrical sandwich shell.

Table 7Effect of radial gradient sandwich on acceleration response of the cylindrical sandwich shell.

The natural mode shapes of cylindrical sandwich shell with gradient core of entangled wire mesh have been analyzed and discussed in detail by the previous work(Wu et al.[32]).The results show that there are 6 obvious modal shapes.The first, second and third modal shapes are distributed as two square elliptical drums,while the fourth modal shape is displayed as three square drums,and the fifth and sixth modal shapes are distributed as four square drums.

4.2.2.Thesinusoidalfixedvibrationtest

Sinusoidal constant frequency excitation is applied to the test sample,and the damping characteristics of the gradient cylindrical sandwich shell with entangled wire mesh under different excitation force amplitudes are observed.The gradient cylindrical sandwich shell with entangled wire mesh in sample C and sample G is tested.The excitation frequency is set to 5 Hz.The excitation force is controlled to 20,25, 30,and 35 N.Figs.16 and 17 demonstrate the hysteresis loops of sample C and sample G obtained from the tests.

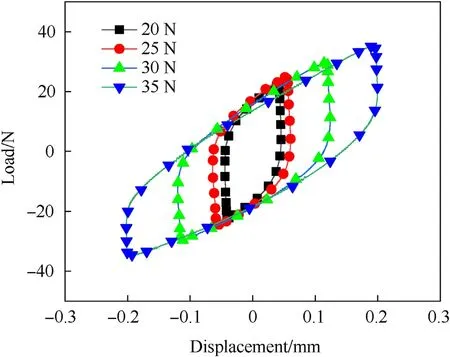
Fig.17.Hysteresis loop of sample C under different excitation forces.

Fig.18.Hysteresis loop of sample G under different excitation forces.

As shown in Figs.17 and 18,as the excitation force increases,the enclosed area of the hysteresis loop becomes larger.The area enclosed by the hysteresis loop represents the amount of energy dissipated in one cycle.The increase in the excitation force increases the displacement,which further increases the extrusion of the skin against the core layer.This causes friction between the wires.

According to the measured test data, Figs.19 and 20 represent the dynamic stiffness and SEA of the gradient cylindrical sandwich shell with entangled wire mesh under constant frequency excitation, respectively.It can be observed that the dynamic stiffness of the gradient cylindrical sandwich shell with entangled wire mesh decreases with the increase of the excitation force.The decrease in the dynamic stiffness of the cylindrical sandwich shell is caused due to the change in the curvature of the compression surface and the non-compression surface of the cylindrical sandwich shell during the loading process.

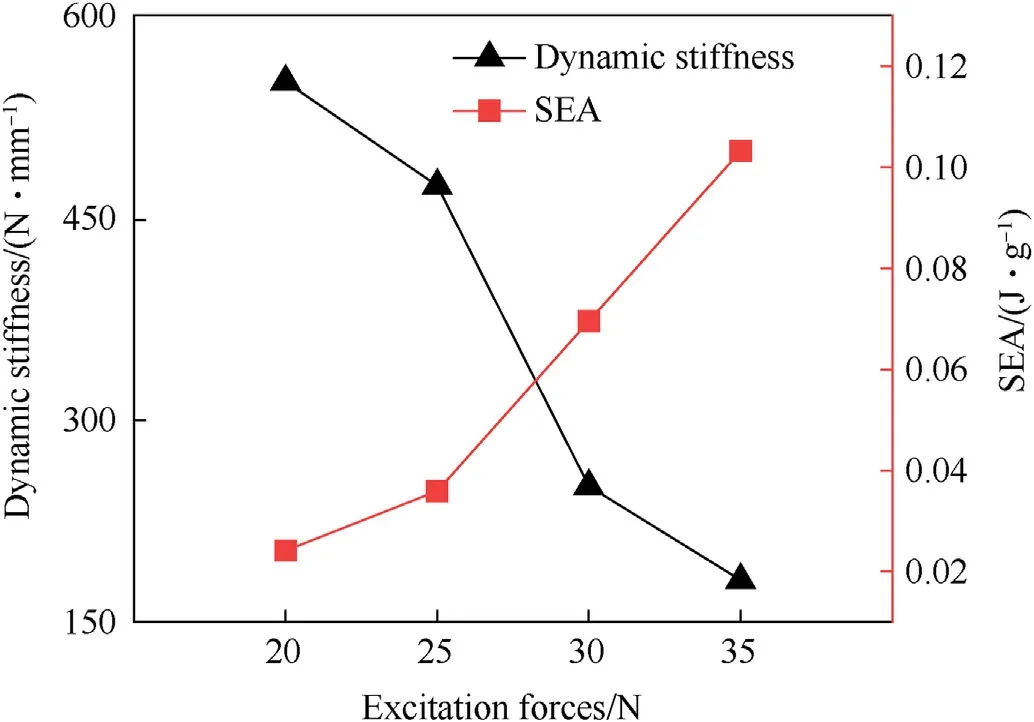
Fig.19.Dynamic stiffness and SEA of sample C under different excitation forces.

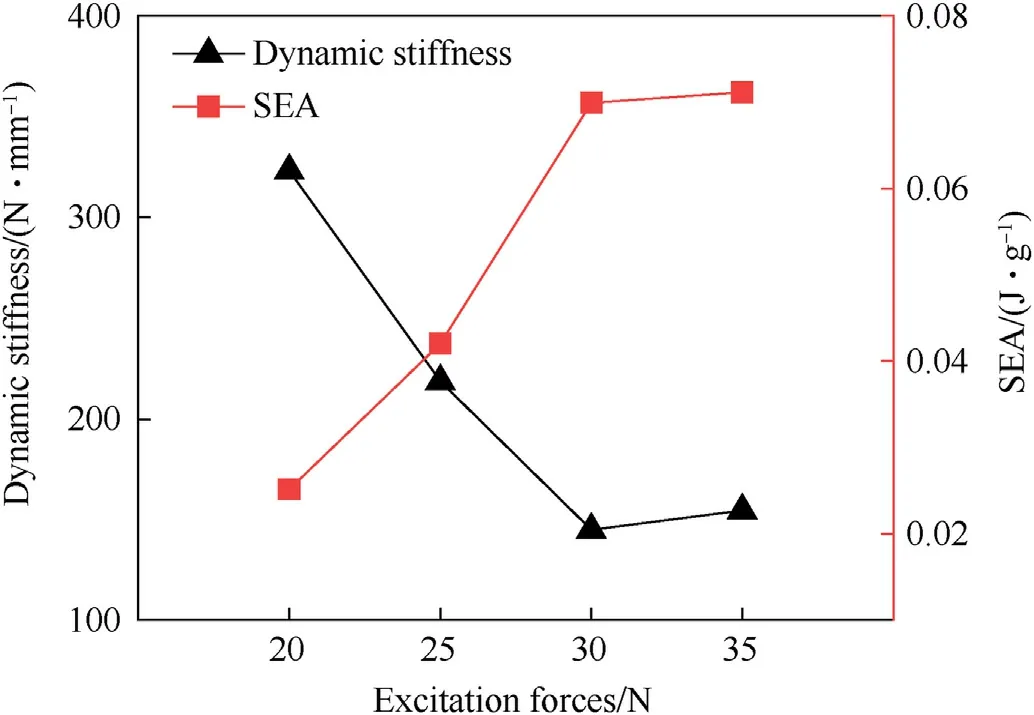
Fig.20.Dynamic stiffness and SEA of sample G under different excitation forces.

The rising excitation force causes an increase in displacement.This leads to more severe frictional energy consumption between the metal wires.The SEA of entangled wire mesh increases with the displacement.In Fig.19,the trend of dynamic stiffness of sample G suddenly changes at the loading condition of 30 N.This is because the deformation of the cylindrical sandwich shell becomes larger.The deformation of the high-density entangled wire mesh located in the outer layer also increases.The extrusion area of the wire increases exponentially.The increasing friction between the wires increases the stiffness beyond the rate at which it weakens as it bucks.

4.3.Analysis of the damping mechanism

Based on the test results, the damping and energy absorption characteristics of the gradient cylindrical sandwich shell with entangled wire mesh are exerted in the quasi-static compression,sinusoidal sweep vibration test,and sinusoidal fixed vibration test.In the quasi-static compression test,the cylindrical sandwich shell is subjected to radial external pressure.It gradually varies from cylindrical to elliptic cylindrical.The skin is deformed,and the core is extruded.The metal wire is pulled using the solder joint.This causes extrusion and friction between the metal wires.The deformation of the radial gradient structure under load is from external side to internal side along the radial direction.The extrusion of the core layer is also from external side to internal side.The stiffness and SEA are determined by the number of wires extruded and rubbed.

The dynamic characteristics and energy dissipation characteristics highlighted in the dynamic test are different under quasistatic conditions.In the sinusoidal sweep vibration test, the influence of radial gradient distribution on natural frequency is more obvious than that in axial gradient distribution.This is due to the change in core density distribution and the strengthening of skin stiffness by solder joints.The high-density part is distributed near both sides of the skin, leading to the increase of solder joints.Therefore, the stiffness's natural frequency increases.In the sinusoidal sweep vibration test, the SEA increases with the increase in exciting force.The metal wires arranged inner the core layer are loaded.The microhelix structure tends to stretch the unwinding.The amount of displacement in the radial direction is different.The shearing between the metal wire layers leads to the friction and stretching of the metal wires, which induces energy absorption.Owing to the difference in the displacement of the skins on both sides,the entangled wire mesh at the non-compressed surface will also produce tension and compression.The tangential movement between the wires leads to grinding and stretching between the wires.The entangled wire mesh in the non-forming direction is pulled and pressed due to the different displacements of the skins on both sides.

5.Conclusions

In this work,the cylindrical sandwich shell with gradient core of entangled wire mesh in the axial and radial directions have been developed.Three typical gradient distributions, i.e., unidirectional distribution, positive and negative symmetrical distributions were introduced.The gradient distribution induced the mechanical responses of cylindrical sandwich shell were analyzed and discussed,including secant stiffness, natural frequency, Specific Energy Absorption (SEA), vibration acceleration level, and so on.The main conclusion can be drawn as follows.

(1) The influence of radial gradient distribution on secant stiffness of cylindrical sandwich shell is remarkable compared to axial one.This is because the radial mechanical response is dominant on the flexible entangled wire mesh core,and the axial mechanical response is dependent on the external and internal skins.

(2) In the axial gradient distribution,the sample B with negative gradient symmetrical distribution in the axial direction has obvious energy consumption characteristics, and the SEA and the vibration acceleration level can reach 0.228 J g-1and 25.47 dB, respectively.

(3) The radial gradient distribution of the core layer has an obvious influence on the natural frequency of the gradient cylindrical sandwich shell.The sample G with unidirectional gradient distribution in the radial direction and maximum density in the external core layer has remarkable vibration attenuation effect.The SEA and the vibration acceleration level can reach 0.212 J g-1and 27.45 dB, respectively.

(4) Under the dynamic loading conditions, the excitation magnitude is negatively correlated with the dynamic stiffness of the gradient cylindrical sandwich shell with entangled wire mesh and positively correlated with the SEA.

Credit author statement

Xin Xue:Supervision,Conceptualization,Methodology,Writing- review & editing.Chao Zheng: Conceptualization, Methodology,Writing- original draft, Investigation, Data curation, Formal analysis.Fuqiang Lai: Supervision, Conceptualization, Methodology,Review & editing, Funding acquisition.Xueqian Wu: Conceptualization, Methodology, Writing - review&editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

Supports from the National Natural Science Foundation of China(Grant No.12272094, No.52205185 and No.51975123) and the Natural Science Foundation of Fujian Province of China (Grant No.2022J01541 and No.2020J05102) and the Key Project of National Defence Innovation Zone of Science and Technology Commission of CMC (Grant No.XXX-033-01) and are gratefully appreciated.