Dependence of impact regime boundaries on the initial temperatures of projectiles and targets

Stefano Signetti, Andreas Heine

Fraunhofer-Institut für Kurzzeitdynamik, Ernst-Mach-Institut, EMI, Ernst-Zermelo-Str.4, 79104 Freiburg im Breisgau, Germany

Keywords: Ballistic impact Thermal effects Metallic targets Energy partitioning Homologous temperature

ABSTRACT Towards higher impact velocities, ballistic events are increasingly determined by the material temperatures.Related effects might range from moderate thermal softening to full phase transition.In particular,it is of great interest to quantify the conditions for incipient or full melting of metals during impact interactions,which result in a transition from still strength-affected to hydrodynamic material behavior.In this work,we investigate to which extent the respective melting thresholds are also dependent on the initial, and generally elevated, temperatures of projectiles and targets before impact.This is studied through the application of a model developed recently by the authors to characterize the transition regime between high-velocity and hypervelocity impact, for which the melting thresholds of materials were used as the defining quantities.The obtained results are expected to be of general interest for ballistic application cases where projectiles or targets are preheated.Such conditions might result, for example, from aerodynamic forces acting onto a projectile during atmospheric flight, explosive shapedcharge-jet formation or armor exposure to environmental conditions.The performed analyses also broaden the scientific understanding of the relevance of temperature in penetration events, generally known since the 1960s, but often not considered thoroughly in impact studies.

1.Introduction

The physical processes occurring during impact events evolve and also may change abruptly [1].They are directly related to the constitutive,failure and volumetric behavior of the materials under extreme pressures and strain-rates.

In a precedent work[2],it has been analytically shown how for metals a transition regime between the high-velocity conditions,partly fluid-like but still strength-dominated, and hypervelocity penetration associated with fully hydrodynamic behavior can be quantitatively characterized.This domain, defined in Ref.[2] by melting thresholds of the projectile and target materials, features an overlapping of the characteristic phenomena of the respective regimes and, therefore, shows a very complex phenomenology as discussed thoroughly in the review of Ref.[1], namely: strain-rate hardening, thermal-softening from either deviatoric and volumetric deformation,strain localization,fracture and fragmentation,and melting.In a recent work [3], a transition towards hypervelocity in the phenomenology of kinetic energy partitioning into temperature increase has also been characterized and quantified via molecular dynamics simulation.These peculiar characteristics are expected to challenge the experimental and numerical investigations as well as the physical interpretation of results in this intermediate domain.

Typically,the impact velocities or strain-rates alone are used for a coarse definition of regimes characterized by the different responses of materials [1].While the above-mentioned works have highlighted the fundamental importance of accounting for the material properties, still a thorough investigation is necessary about the influence of initial projectile and target temperatures.Related effects on impact penetration are known and have driven attention since the early phases of impact research[4-6].However,these are rarely considered in the numerical modeling or interpretation of results when thermal conditions are far from the material melting thresholds.

The assumption of room temperature for both projectile and target represents and idealized scenario, quite uncommon in real applications.Indeed, non-ideal impact conditions in relation totemperature may easily originate from different sources.We mention,for example:(i)aerodynamic forces acting on a projectile during atmospheric flight, which may heat up the projectile by several hundred degrees,ranging from about ΔT= 100 K for artillery shells[7]up to ΔT=400-500 K for kinetic energy penetrators[8-11]; (ii) explosive shaped-charge-jet formation where the hypervelocity jet temperature can rise by several hundreds of Kelvins[12]and can also approach the material melting thresholds(see,for example, Ref.[13] where temperatures of about 1200 K are reported for copper jets);(iii)exposure of armors and shields to harsh environmental conditions,with temperatures ranging,for example,between about 100 and 400 K for low-earth-orbit (LEO) satellites[14,15].

Table 1Threshold velocities, calculated for T0，p =T0，t = 300 K, for some material combinations of interest in terminal ballistics.For heterogeneous projectile/target combinations it is indicated whether the incipient and full melting conditions associated to the lower and upper bound velocities,respectively,are met in the projectile(p)or target(t)material.Material properties used for computations are reported Table A1 in the Appendix.This table integrates results reported in Ref.[2] with additional material combinations.

The purpose of this work is to assess the influence of both projectile and target initial temperatures, up to about the respective melting thresholds, on the characteristic impact velocities associated to melting conditions of projectile and target materials.Therefore,by exploiting the model described in Ref.[2],the results shown in this work aim at generalizing earlier findings on the topic[1,2] and provide an insight on the materials impact behavior for actual pre-impact thermal conditions occurring in both ballistic experiments,either in light-gas gun laboratory or open field,and in real scenarios.

2.Summary of the shock-based energy partitioning model

The characterization of the impact melting thresholds as in Ref.[2]relies on a shock-based partitioning model which computes the energy density of the projectile and target materials arising from impact loading at the crater propagation front.In the following, this model is briefly recalled and further discussed.The sudden increase of the internal energy due to shock compression in the projectile(p)and target(t)at the interface of the two bodies can be synthetically expressed, in per volume terms,as

where v0is the projectile impact velocity andthe corresponding specific impact kinetic energy;μp=（（up/ut）/（1+up/ut））2and μt=（up/ut）/（1+up/ut）2are velocity-dependent partition factors describing the fraction ofk0converted into internal energy for projectile and target, respectively, whereutis the material (particle) velocity of the target,which is computed through shock-impedance mismatch considerations between the colliding materials[2],andup=v0-utis thematerial velocity in the projectile.Eq.(1) shows that the impact velocity is an important parameter to classify the phenomenological impact regimes but also the material properties have a significant role in the induced pressure levels by determining μ（p/t）,and therefore must not be neglected [2].

Table 2Regime boundaries for WHA projectile against steel target at different homologous temperatures,referenced at 300 K,for the two bodies.Each cell reports,in the order,the two impact velocities,in km·s-1,corresponding to incipient and full melting conditions,vlow and vup,respectively(cf.Fig.1).For each temperature combination,it is also specified whether the thresholds are met in the projectile(p) or in the target (t).Material properties used for computations are reported in Table A1 in the Appendix.

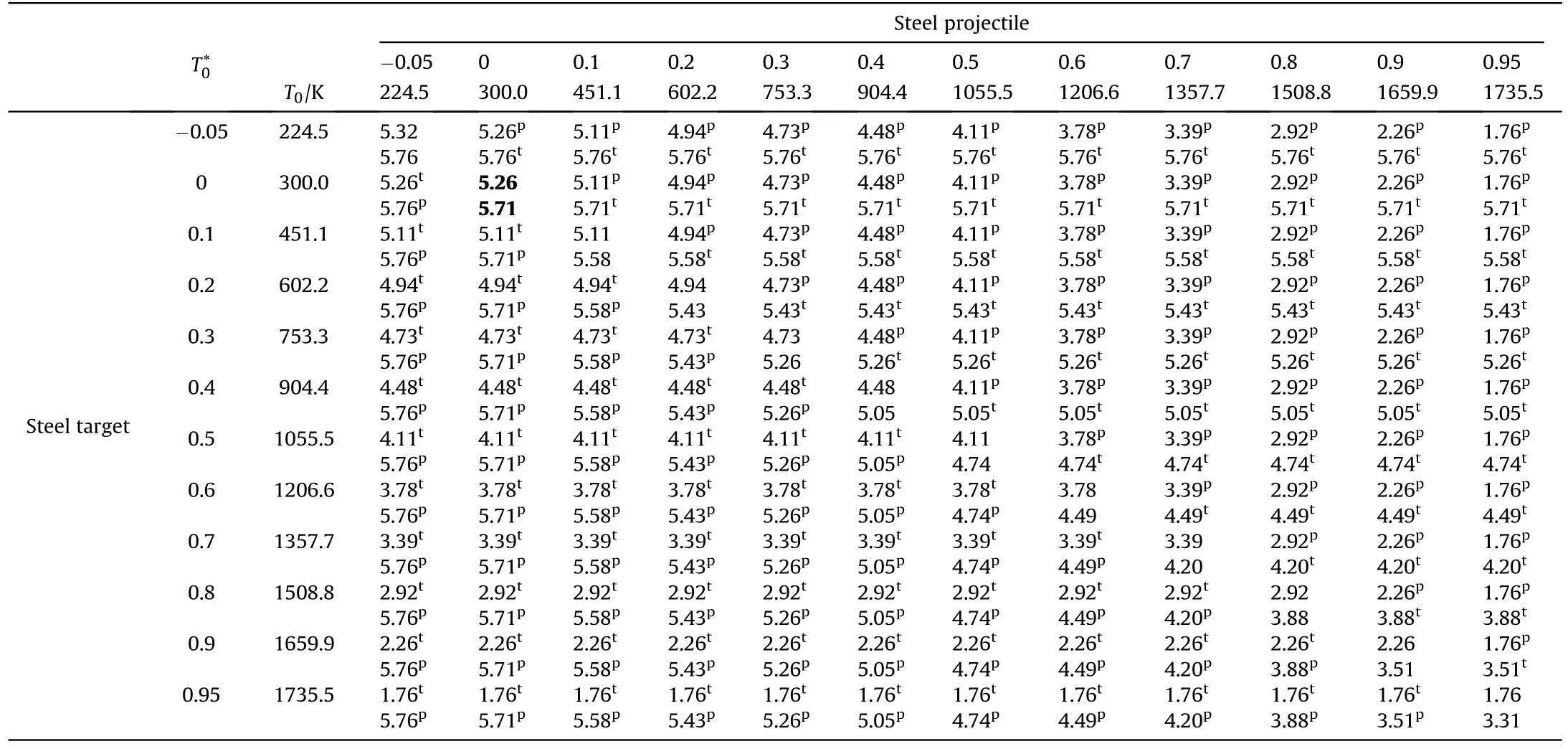
Table 3Regime boundaries for steel projectile against steel target at different homologous temperatures,referenced at 300 K,for the two bodies.Each cell reports,in the order,the two impact velocities,in km·s-1,corresponding to incipient and full melting conditions,vlow and vup,respectively(cf.Fig.1).For each temperature combination,it is also specified whether the thresholds are met in the projectile(p)or in the target(t).In the case of impact of identical materials,they occur indiscriminately in either projectile and target when their initial temperature is the same, cf.entries along the table diagonal.Material properties used for computations are reported in Table A1 in the Appendix.

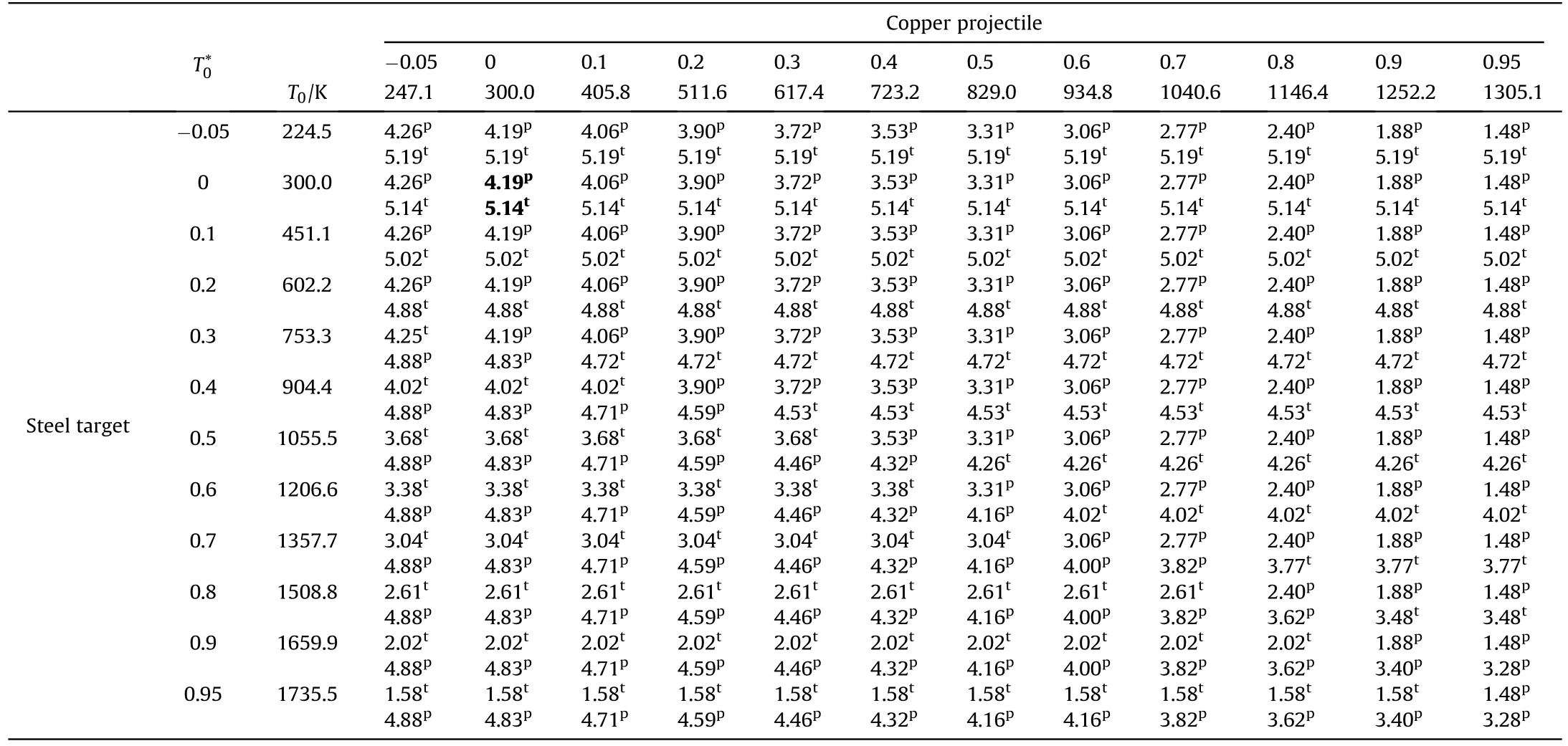
Table 4Regime boundaries for copper projectile against steel target at different homologous temperatures,referenced at 300 K,for the two bodies.Each cell reports,in the order,the two impact velocities, in km·s-1, corresponding to incipient and full melting conditions, vlow and vup, respectively (cf.Fig.1).For each temperature combination, it is also specified whether the thresholds are met in the projectile (p) or in the target(t).Material properties used for computations are reported in Table A1 in the Appendix.

The retained internal energy in either projectile or target materials after a full shock compression-release cycle - under the assumption that the unloading isentrope can be approximated by the shock Hugoniot[2] in the pressure-density (p-ρ) plane - is:

The incipient melting conditions for each phase are met when the respective retained internal energies,given by Eq.(2),equal the following quantity:

wherecvis the specific heat capacity at constant volume andTmis the melting temperature.We highlight thatemis also depending on the initial temperatureT0of the material.A further amount of energy,corresponding to the latent heat of fusion(efus)is necessary to reach the complete melting of each phase, without further increase in the temperature.Therefore,complete melting eventually occurs when the following condition is satisfied:

We remark that melting conditions here relate to the volume in the interaction zone, not to the full projectile or target.It is then possible to identify the values of the impact velocity v0at which the threshold conditions related to phase transitions, above expressed by Eqs.(3) and (4), are reached for the projectile and target,respectively.Therefore, a total of four characteristic velocities can be identified,corresponding to incipient(vm，p,vm，t)and full melting(vfus，p,vfus，t)thresholds of projectile or target material,respectively.The transition regime is then defined by the velocity range corresponding to [2]:

Note that in case of projectile and target of identical materials and same initial temperatures is vm，p=vm，tand vfus，p=vfus，tsince both the melting thresholds and stored energies of projectile and target are equal,cf.Eq.(1)forut=up.When the impact velocity is higher than vupthe directly interacting parts of both projectile and target are liquid, thus their behavior is ideally hydrodynamic.However,this does not imply that full melting would always occur when materials display hydrodynamic-like behavior,rather both typically go along with each other [1].

Table 1 reports the regime boundaries for several material combinations of interest in terminal ballistic assuming for both projectile and target materials an initial temperature of 300 K.In Refs.[1,2]the computations have been shown to be consistent with direct experimental observations of melting thresholds[16],related impact velocities [17-19] and, indirectly, with measures of kinetic energy partition into quasi-stationary target temperature increase[20].Qualitative considerations on regime boundaries were further supported by the analysis of penetration efficiency curves [2,21].

The results are also consistent with the use of surrogate material for scaled experiments[19,22-24].For example,a factor of about 1/3 and 1/2 in the velocity-scaling when using Cadmium →Cadmium or Zinc →Zinc impacts, respectively, to replicate hypervelocity conditions of Aluminum → Aluminum [25,26] is well reflected by the ratios of the computed characteristic velocities corresponding to material melting thresholds (vlow，Cd/ vlow，Al=0.356, vup，Cd/vup，Al= 0.366, vlow，Zn/vlow，Al= 0.520, vup，Zn/ vup，Al=0.523, cf.Table 1).

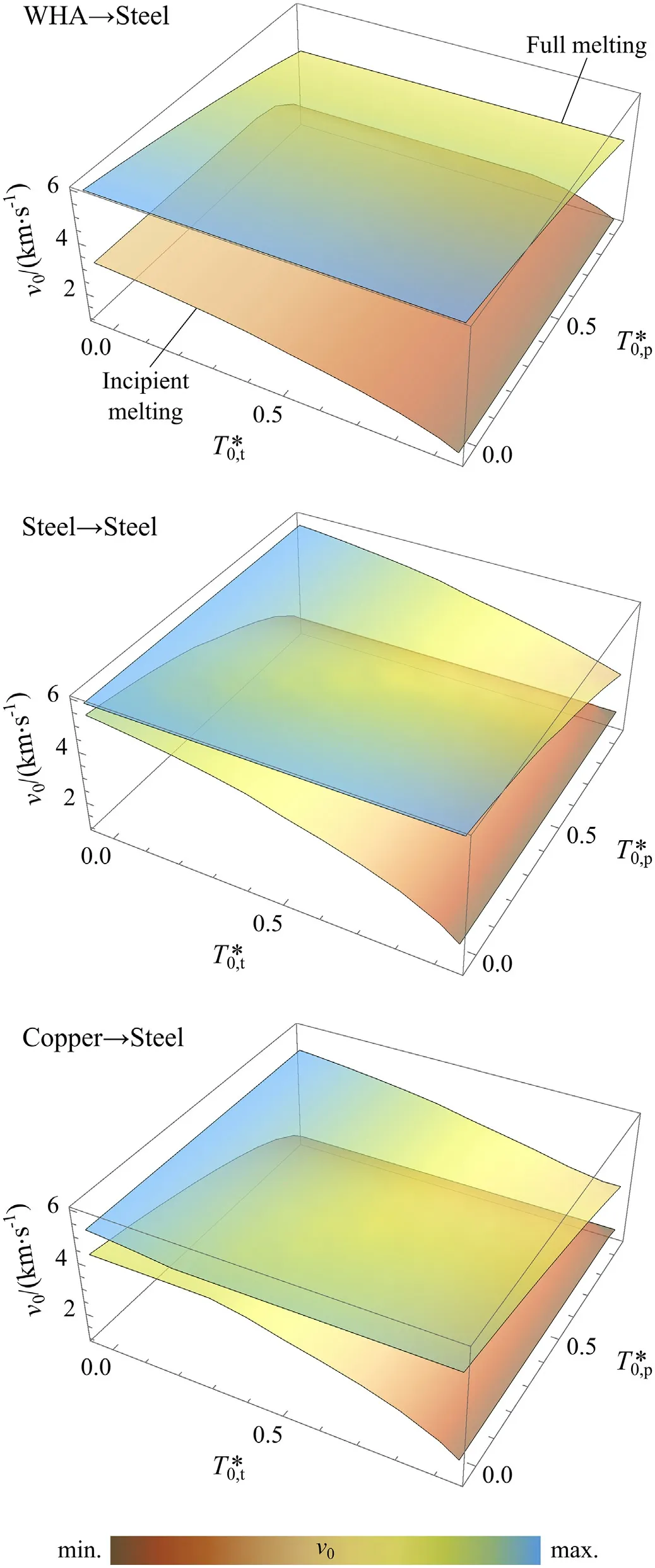
Fig.1.Dependency of the characteristic melting thresholds of the impact event in metals, vlow and vup, respectively, on the initial temperatures of projectile and target for selected material combinations.Some of the computed values of these boundary surfaces are reported in Tables 2-4.

3.Results and discussion

The computations reported in this section are rationalized in terms of the dimensionless temperature termT*= （T-Tref）/（Tm-Tref）[27],also known as homologous temperature,whereTrefis a reference temperature, generally corresponding to room temperature.In this work,the explored domain of initial projectile and target temperatures is-0.05 ＜＜0.95,withTref= 300 K for all computed cases.Therefore, we account for pre-heating temperatures up to close to the melting point of materials while the lower bound can be seen as representative of harsh lowtemperature conditions, about -25°C to -50°C depending onTmof the considered materials in this study.For the latter purpose,we extend the homologous temperature slightly toward negative values.

Among the different material combinations reported in Table 1,we here include extensive computation for selected exemplary results, namely:

Fig.2.Representative sections of the 3D diagrams of Fig.1 at= 0 = const., left panels, and = 0 = const., right panels.The dots report the discrete computed values from Tables 2-4 while the connecting lines are just a guide to the eye,still representing a good approximation of the actual boundaries.The different colors identify whether the incipient and full melting conditions occur in the projectile (orange), in the target (blue) or undetermined (dark grey).

·WHA(TungstenHeavyAlloy)→Steelas representative case of a high-density projectile penetration where,generally, the incipient melting threshold is first overcome in the target material and full melting at the very end occurs in the projectile material;

·Steel→Steelas representative of impact between identical materials;

·Copper→Steelas representative case for a shaped-charge jet penetration where,generally,the incipient melting threshold is first overcome in the penetrator (solid jet) and full melting ultimately occurs in the target material.

The computations for the three material configurations, calculated for discrete initial temperature combinations within the above defined domain,are reported in Tables 2-4.The evolution of the impact melting thresholds at different initial temperatures is then visualized in the form of three-dimensional diagrams (v0vs.) in Fig.1.To better highlight the role of the initial temperatures, Figs.2 and 3 report selected cross-sections of the surfaces for constant initial temperature of either projectile or target.

Fig.3.Representative sections of the 3D diagrams of Fig.1 at =0.5=const.,left panels,and =0.5=const.,right panels.The dots report the discrete computed values from Tables 2-4 while the connecting lines are just a guide to the eye,still representing a good approximation of the actual boundaries.The different colors identify whether the incipient and full melting conditions occur in the projectile (orange), in the target (blue) or undetermined (dark grey).

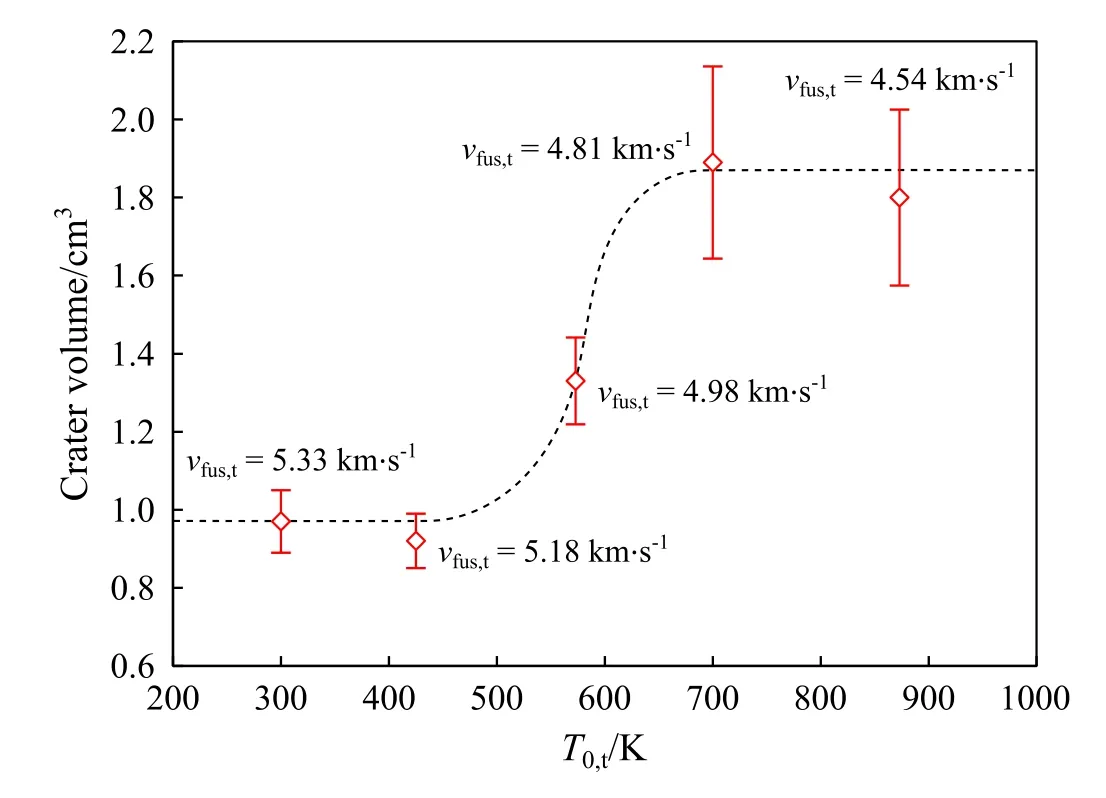
Fig.4.Crater volume resulting from impact of 0.18 g,5.01 km·s-1 steel spheres against copper as a function of the target temperature from experiments by Allison et al.[5].An increase of the crater volume occurs around T0，t = 573 K.Consistently, the analytical model discussed in the present work predicts that above this initial target temperature the full melting threshold is overcome for the heated copper target at the given impact velocity.The threshold velocities for full melting of the target predicted by the model for the different experimental temperature conditions are reported in the graph.

First, it further clearly emerges that the computations reported in Ref.[2] and Table 1 are a particularization corresponding to the ideal condition, while the location of both velocity boundaries corresponding to incipient and full melting conditions may significantly change for different initial temperatures, and so does their mutual distance.

In the case of WHA-onto-steel impact, for constant initial temperature of the projectile the upper bound velocity is unaffected by the target temperature, while the velocity corresponding to the lower bound (incipient melting condition for the target) monotonically decreases approaching the steel melting temperature(Fig.2).For constant target temperature,vupconsistently decreases with increasing initial temperature of the projectile.The lower bound velocity remains constant, except for higher initial temperatures of the projectile,namely≿0.8,where also vlowis defined by the incipient melting condition of the projectile (Table 2).Similar trends are observed at room (= 0, Fig.2) and intermediate(=0.5,Fig.3)initial temperatures of both materials.

For steel-onto-steel impact the symmetry given by identical materials is evidenced in Figs.2 and 3.The cross-section at intermediate temperatures (Fig.3) highlights the complexity of the melting surfaces, showing that they follow complex and counterintuitive trends depending on whether for the specific temperatures combination the overcoming of the melting threshold switches from the projectile to the target material, or vice versa.Interestingly, the minimum difference between vlowand vup, cf.Figs.2 and 3, appears when the projectile and the target have the same initial temperatures, reflecting the symmetric material properties.In the nearby of these configurations,a relatively small increment in the impact velocity may result in quite different phenomenology of the impact event.

Last, the case of copper-onto-steel shows, to some extent, a more generalized behavior where the trend of melting threshold cannot be intuitively defined a-priori.Interestingly, similar to the steel-onto-steel case, a narrow minimum distance between the melting boundaries emerges, showing that the material phenomenology can be very sensitive to the impact velocity under specific initial thermal conditions.

As a further and indirect verification of our model, we finally report the impact experiments by Allison et al.on copper targets heated up to 900 K [5].Fig.4 depicts the evolution of the crater volume in heated targets hit by steel spheres at 5.01 km·s-1.It is observed a sharp increase in the crater volume when the target is pre-heated above 573 K.The model reported in the present work predicts that forT0，t≿570 K the full melting condition in the target is met for the adopted impact velocity, namely vfus，t（T0，t）＜v0.Similar experiments were conducted in Ref.[4] up to target temperatures of 1255 K (close to the melting point of copper, cf.Table A1):there,an abrupt change in crater volume is not observed since the maximum adopted impact velocity is 3.5 km·s-1and,consistently with our predictions, the threshold condition is not met even at the maximum adopted initial target temperature, being vfus，t（T0，t=1255 K）= 3.76 km·s-1.

4.Conclusions

In this work we have exploited a model developed in a precedent article[2]to generalize the computation of the boundaries of the material melting threshold in impact events of metals for arbitrary initial temperatures of both projectile and target.Selected results for representative material combinations of interest in terminal ballistics have been shown.Additional results from the literature were also used for further validation of the model predictions.This work further highlights how a characterization of impact regimes on the basis of the velocity is meaningful only in combination with material propertiesandactual initial temperatures.While the used definition of the regime boundaries for highvelocity and hypervelocity impact is not unique, the underlying model clearly is capable of quantifying to which extent the increased initial temperatures of projectiles and targets may bring the phenomenology closer to hydrodynamic behavior.We believe that the generalized results shown in this work extend the understanding of impact phenomenology for hydrocode modeling of impact events, for the interpretation of ballistic experiments, and for effects assessment.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge funding by Bundesministerium der Verteidigung (BMVg), Germany.

Appendix A.Material parameters

Table A.1Material properties used for the analytical computation in this study and related source references.