The prediction of projectile-target intersection for moving tank based on adaptive robust constraint-following control and intervaluncertainty analysis

Cong Li , Xiuye Wng ,*, Yuze M , Fengjie Xu , Guoli Yng

a The School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing, 290014, PR China

b Inner Mongolia North Heavy Industries Co., Ltd., Baotou, 014033, PR China

c Nanjing Chenguang Group Co., Ltd., Nanjing, 210006, PR China

Keywords: Tank stability control Constraint-following Adaptive robust control Uncertainty analysis Prediction of projectile-target intersection

ABSTRACT To improve the hit probability of tank at high speed,a prediction method of projectile-target intersection based on adaptive robust constraint-following control and interval uncertainty analysis is proposed.The method proposed provides a novel way to predict the impact point of projectile for moving tank.First,bidirectional stability constraints and stability constraint-following error are constructed using the Udwadia-Kalaba theory, and an adaptive robust constraint-following controller is designed considering uncertainties.Second,the exterior ballistic ordinary differential equation with uncertainties is integrated into the controller,and the pointing control of stability system is extended to the impact-point control of projectile.Third, based on the interval uncertainty analysis method combining Chebyshev polynomial expansion and affine arithmetic, a prediction method of projectile-target intersection is proposed.Finally, the co-simulation experiment is performed by establishing the multi-body system dynamic model of tank and mathematical model of control system.The results demonstrate that the prediction method of projectile-target intersection based on uncertainty analysis can effectively decrease the uncertainties of system, improve the prediction accuracy, and increase the hit probability.The adaptive robust constraint-following control can effectively restrain the uncertainties caused by road excitation and model error.

1.Introduction

The first-round-hit probability are important indicators of tank[1].With the improvement of the requirements for the maneuverability of tank and the increase of the intensity of battle, the stability of the barrel decreases sharply,which seriously decreases the hit probability of tank.This requires that the fire control system(FCS) can still maintain the stability of barrel, track the target quickly and predict the impact point of projectile accurately.Hance,it is essential to enhance the control of stability system and prediction method of projectile-target intersection so that improve the hit probability.

The stability control system of tank is a significant component of FCS.Most of the research on stability control is to simplify the horizontal and vertical control to a linear model that can be characterized by the transfer function [2].Thus, the theories and methods of linear systems, such as PID control, are directly introduced to design the controller [3-5].With the increase of the complexity of the model, uncertainties, time-varying and disturbance, the classical control theory has been unable to meet the requirements of stability control.At present, some scholars have introduced modern control theory into stability control, for instance, active-disturbance-rejection control, adaptive control,and neural network control [6-12].These methods greatly enrich the way of stability control of tank.

Some scholars have introduced the constraint-following control method into stability control of tank[13-15].Constraint-following control, which is derived from Udwadia-Kalaba (U-K) theory, is a model-based state feedback control method [16,17].Chen et al.[18,19]transformed the problems of stability control and trajectory tracking control into constraint-following control founded on U-K theory.The constraint-following control depends on the inherent characteristics of the mechanical system, and the control effect is more in line with the requirements of dynamics.This method can not only realize the parallel control of multiple motion characteristics,but also consider the influence of complex uncertainties.The constraint-following method has guided significance for the bidirectional stability control of tank.

However, the prediction of impact point is not considered in above-mentioned stability control method.The FCS needs to solve the ballistic and predict the impact point in real time, which is an essential prerequisite for tank to hit the target.The current research on tank firing is biased towards target search and recognition[20,21].In the traditional FCS, the fitting of firing table is used to approximately solve the exterior ballistic(EB)problem[22,23].The accuracy of the fitting of firing table is low,and the ballistic match is poor, and the non-standard conditions need to be modified.Therefore, with the improvement of the computing power of the FCS computer,it is necessary to study the direct numerical solution of the exterior ballistic ordinary differential equation(EB-ODE).Ma et al.[24] convert the impact point of projectile into the angle control of the control system,and realize the integration of the sixdegree-of-freedom (6-D) EB-ODE and the control system.Nevertheless, this study does not consider the uncertainties of EB.

The EB is the most typical uncertain process in gun firing [25].The initial disturbance and meteorological conditions will affect the flight trajectory and attitude of projectile [26].These uncertainty factors make the impact point of projectile fluctuate in a certain area,which will affect the hit probability.Hence, it is necessary to accurately express the relationship between the projectile's impact area and target area.At present, the prediction of projectile-target intersection is involved in target damage [27,28] and missile precision striking [29].In this paper, the term will be introduced to express the relationship between the projectile's impact area and the target area,and to predict the projectile-target intersection.The EB-ODE with uncertainties is integrated into the control system,which will decrease the stability of the control system.Through the uncertainty analysis (UNA) for the EB-ODE, the influence of uncertainty parameters on impact point of projectile can be obtained.It has important theoretical and engineering value for real-time prediction of impact point coordinates and improving the stability of control system.

The stochastic method [30] is a traditional method to describe uncertainty parameters, where uncertainty parameters are expressed as random processes with the exact probability distribution.Although, in the problem of tank firing, some uncertain parameters of EB, such as the initial disturbance of projectile, are sometimes difficult to obtain,and it is relatively easy to obtain the possible range of these uncertainty parameters.The interval method [31] uses the upper and lower bounds of parameters to describe the uncertainties of parameters, which is more adaptive than the probabilistic model.At present, the interval UNA method has been widely used in engineering [32-35].In this paper, an interval UNA method based on Chebyshev polynomial expansion(CPE)[35-37]and affine arithmetic(AA)[38-41]is used to analyze the uncertainties of EB.

The contributions of this paper are four-fold.First,the dynamic model of bidirectional stability system of tank in generalized coordinate is constructed.An adaptive robust constraint-following controller for bidirectional stability is designed considering uncertainties such as system modeling error and external disturbance.Second, a 6-D EB-ODE with uncertainties is introduced, and the constraint-following error are established through coordinate transformation and geometric relationships.By combining the EBODE with the controller,stability control of the barrel is extended to the impact point control of the projectile.Third,using CPE and AA,a prediction method of projectile-target intersection based on interval UNA is proposed.Finally, the multi-body system dynamics model of tank is constructed, and the co-simulation between control system and dynamics model is realized,which indicate the advantage of the proposed method.

2.Constrained bidirectional stability system of tank

2.1.Dynamic equations of the bidirectional stability system

In the analytical dynamic analysis of bidirectional stability system,it can usually be simplified as shown in Fig.1.This model has two dimensions of load, namely the turret load and barrel(including the breech and cradle) load.L1is the rotation radius of turret,andL2is the distance from muzzle to trunnion.φ1and φ2are the horizontal rotation angle and the vertical rotation angle in the ground coordinate system, respectively.The weight of turret and barrel ism1，2respectively.To derive the dynamic equation of the bidirectional stability system[42],the kinetic energy of the turret is

Select the turret plane as zero potential energy surface,then the potential energy

The kinetic energy of the barrel is

The initial potential energy is

According to Spong and Vidyasagar [43], the Lagrange function of the system can be obtained as

According to the Euler-Lagrange equation,the driving torque τ1and τ2of the turret and barrel are

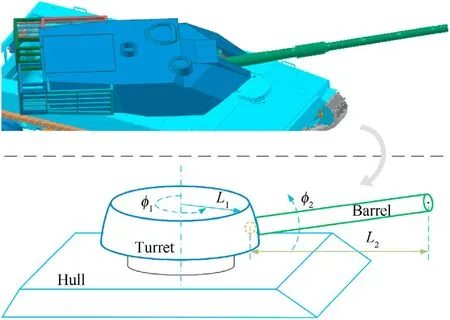
Fig.1.Simplified model of the bidirectional stability system.

Therefore, the dynamic equations of the bidirectional stability system are

in whichd（t） is the external disturbance.

2.2.Constrained mechanical systems with uncertainties

Due to modeling error and irregular structure,the bidirectional stability system can be regarded as mechanical system with uncertainties.The dynamic equation of mechanical system with uncertainties is [44,45].

in whichq∈Rnis system coordinate vector,is system speed vector andis system acceleration vector.σ∈∑⊂Rpare system uncertainty parameters.Here, ∑⊂Rpis a compact that symbolizes the possible bound of σ.τ is system control input.Moreover,M（q，σ，t）＞0 is the inertia matrix,is Coriolis/centrifugal force,G（q，σ，t） is gravitational force, andis external disturbance and frictional force.

If the mechanical system is subject to a set of constraints, the constraint equation as follows:

in whichm≤n,Ali（·） andcl（·） areC1.The constraint can be described as a matrix.

in which A = ［Ali］m×n, c = ［c1c2…cm］T.The second-order form of constraints is [46]

Remark.For mechanical systems with uncertainties and unlimited initial conditions, it is generally only required that the system approximately meet the constraints to ensure the normal operation of the mechanical system, that is, approximate constraint-following control.Driven by approximate constraint control τ, define the constraint-following error as

where β = ［β1β2…βn］T.

Remark.The β can be regarded as the tracking object.

Theorem 1.Consider the nominal system Eq.(9) and the constraint Eq.(12).The constraint force [47].

Remark.Here, the uncertainties of the system are known.However, in engineering, most of the uncertainties are unknown,and the control methods for unknown uncertainties will be discussed later.

2.3.Target tracking constraints of bidirectional stability system

Convert Eqs.(7) and (8) into the form of Eq.(9) and let q:=［φ1φ2］T,τ:=［τ1τ2］Tand

where

Define the tracking target angle as φd= ［φ1dφ2d］T, which is a dynamic variable.Thus, the target error is defined as

By deriving Eq.(25),the second-order constraints are as follows:

According to Eq.(11) and Eq.(12), it can be obtained as

According to Eq.(13), the constraint-following error can be constructed to be

Remark.Through the above analysis, the problem of target tracking can be transformed into how to design an appropriate controller τ=［τ1τ2］Tto make the controlled system Eq.(9) meet the expected constraints Eqs.(11) and (12).

3.Adaptive robust constraint-following control

From the view of control,while the uncertainty of the system is known,the controller can be designed to make the system meet the constraint requirements.Although,the tank is excited by the road,so that the uncertainty of the controlled system is unknown.Therefore, this section will use a kind of adaptive robust control strategies [18] to the entire (uncertain) controlled system (9)approximately meet the expected constraints Eqs.(11) and (12).

DecomposeM,CandG, as follows:

whereM,are the nominal parts.ΔM, ΔCand ΔGare uncertain parts.Let

Assumption 1.GivenP∈Rm×m,P＞0, |A|≠0,let

For all （q，t）∈Rn× R, ∃ρE＞1 make

Remark.ρEis an unknown real number.WhileE= 0,W= 0,select ρE= 0.

Let

where κ∈R+.

Assumption 2.(1) There exists unknown constant vector α∈Rk+and known function ∏（·）:（0，+∞）k×Rn×Rn×R→R+for all（q， ˙q，t）∈Rn×Rn×R and σ∈∑as follows

Parameter α is unknown and contains the boundary information of uncertain parameters (the boundaries are unknown).To enable the system to estimate the unknown parameter online, the adaptive law of leakage type is designed as

Remark.The designed adaptive law with a leakage termWhile the system reaches a steady state, thebecomes negative,and α decreases gradually and tends to stabilize in a certain range.The adaptive law of leakage type can effectively control the range of estimated uncertainty and prevent excessive control costs.

Combined with adaptive law, the adaptive robust controller is designed as

Remark.In the controller Eq.(35),the function ofp1andp2is to adjust the system to the vicinity of the target constraints.p3is an adaptive robust control part, which is used to restrain the disturbance of uncertainties to make the system always approximately obey the constraints.

Theorem 2.Let δ（t）:=.While the ideal constraint of the system is Eq.(11), if the mechanical system meets Assumptions 1 and 2,the controller Eq.(35)has the following characteristics[18]:

Remark.In this section, the adaptive robust constraintfollowing controller is designed to make the bidirectional stability system track the target quickly and stably.The EB process will be considered to calculate the target angle.

Fig.2.Schematic diagram of the tank hitting the target.

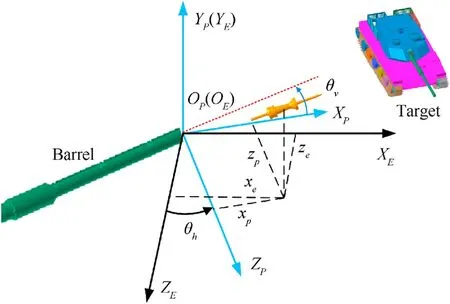
Fig.3.Schematic diagram of coordinate transformation.

4.Angle relation considering the exterior ballistic process

Fig.2 is the schematic diagram of the tank firing the target.Although the tank is direct-fire gun,the EB will also be curved due to the influence of gravity,crosswind and other factors.From Fig.2,when the projectile hits the target, the vertical angle of barrel is greater than vertical angle of impact point to trunnion.Meanwhile,under the influence of the crosswind,the horizontal angle from the impact point to the rotation center of turret is less than that of the turret.Hance, it is necessary to consider the EB process to accurately calculate the impact-point coordinates to obtain the actual target angle.

Remark.Fig.2 shows the ground coordinate systemOEXEYEZE,in which all coordinates are calculated.

4.1.The 6-D external ballistic dynamic model

The 6-D EB dynamics model is adopted, and the nonlinear factors such as crosswind and longitudinal wind are considered,which can be expressed as the following ODEs [25]:

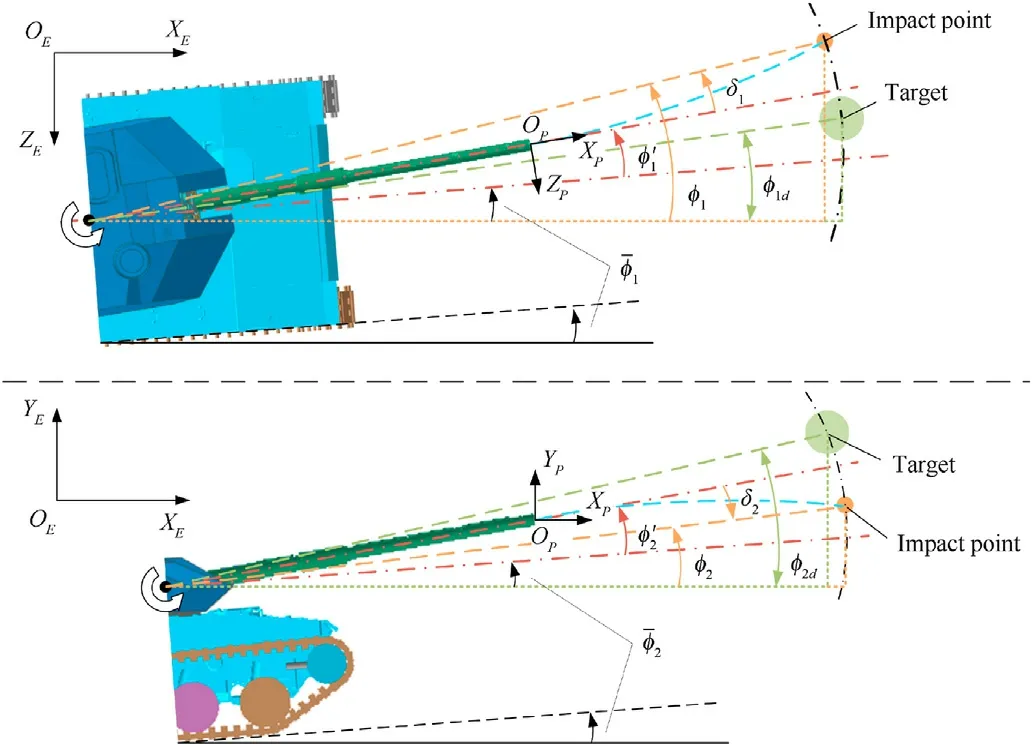
Fig.4.Schematic diagram of the relationship between control angle and target angle.

where vprepresents the velocity of projectile.φ represents the path angle of projectile.ψ1and ψ2represent the vertical and horizontal declination angle, respectively.（X，Y，Z） represent the center of mass of projectile, corresponding to the range, height and lateral deflection of the projectile,respectively.δ1and δ2represent attack angle.represent the vertical and horizontal swinging angular velocity.ICandIArepresent the extreme rotary inertia and equatorial rotary inertia of projectile,respectively.bx,bz,kxz,kzz,kyandkzare represent aerodynamic parameter.andrepresent the projections of wind speed on velocity coordinates,which are as follows:

in which,wxandwzrepresent the longitudinal wind speed and crosswind speed respectively.With the above equations,the flight trajectory and motion attitude of projectile in the atmosphere can be obtained.

4.2.Analysis of actual control angle and target angle

Define the muzzle coordinate systemOPXPYPZPas shown in Fig.3.The muzzle center point is taken as the origin of muzzle coordinate system,theOPYPaxis is perpendicular to the ground,theOPXPaxis is the projection of the direction pointed by the barrel in ground coordinate system, and theOPZPaxis is determined in accordance with the right-hand rule.

Remark.(1) The muzzle coordinate system established is the ground coordinate system in EB-ODE,which is obtained by rotating θharound theYaxis of ground coordinate system in this paper.

(2) The coordinate transformation relationship is

After the establishment of the EB, the control process of target tracking is as follows.

(1) Judge the straight-line distance from the target and calculate the firing distance;

(2) Solve the EB-ODE and obtain the coordinates of projectile's impact point under the current firing distance(in the muzzle coordinate system);

(3) Through coordinate transformation, the coordinates of impact point are converted to the ground coordinate system;

(4) From Fig.4, the absolute control angle φ1，2and target angle φ1d，2dof the control system are obtained according to the coordinates of projectile and target in ground coordinate system.The relationship between the actual control angleand absolute control angle φ1，2is

(5) The constraint-following control can be carried out according to Eq.(25).

Remark.The angles marked in Fig.4 can be read directly by the sensor or calculated indirectly according to the position relationship.

5.The interval uncertainty analysis of exterior ballistic

Theoretically, the impact points of each projectile are different.These differences will affect the hit probability of tank.As shown in Fig.5, the projectile's impact point is a random point within a certain area (shaded area).Hence, it is necessary to describe the projectile-target intersection of the tank on the move.

Fig.5.Schematic diagram of EB uncertainties.

5.1.Description of projectile-target intersection

In the prediction of projectile-target intersection, the midpoint coordinates of the target area are selected as tracking point.Due to the existence of uncertainties, the coordinates of the projectile's impact point at different times are random but bounded.While the EB process is considered in control system, the uncertainties of EB will affect the stability of control system.Therefore,the situation of projectile-target intersection is described as follows.

As shown in Fig.6, assuming that the dotted line area is the control effect,t1,t2,andt3represent a projectile-target intersection at the control boundary,respectively.One of the two cases oft1andt2is excellent and the other is very poor.These two cases with poor stability can be transformed into each other.On the other hand,the intersection situation represented byt3is the error control between the central point coordinates of projectile's impact area and target area, which has excellent stability.Therefore, it is assumed that the coordinates of central point of projectile's impact area are used as the control object in each calculation, which can not only enhance the stability of system, but also improve the prediction accuracy.The interval boundary of dynamic response of the EB-ODE can be calculated in real time by using the method of the UNA.Then the coordinates of the central point of impact area are calculated according to the interval boundary coordinates, which is used as the object of error control.

Remark.To solve the boundary response of the projectile's impact area more efficiently in real-time, an interval UNA method based on the combination of CPE and AA will be proposed below.

5.2.Chebyshev polynomial expansion

The 6-D EB-ODE mentioned above takes a long time to calculate.After it is integrated into the controller, the impact point needs to be solved in real-time.Therefore, in this section, the CPE will be introduced to approximate the EB-ODE.

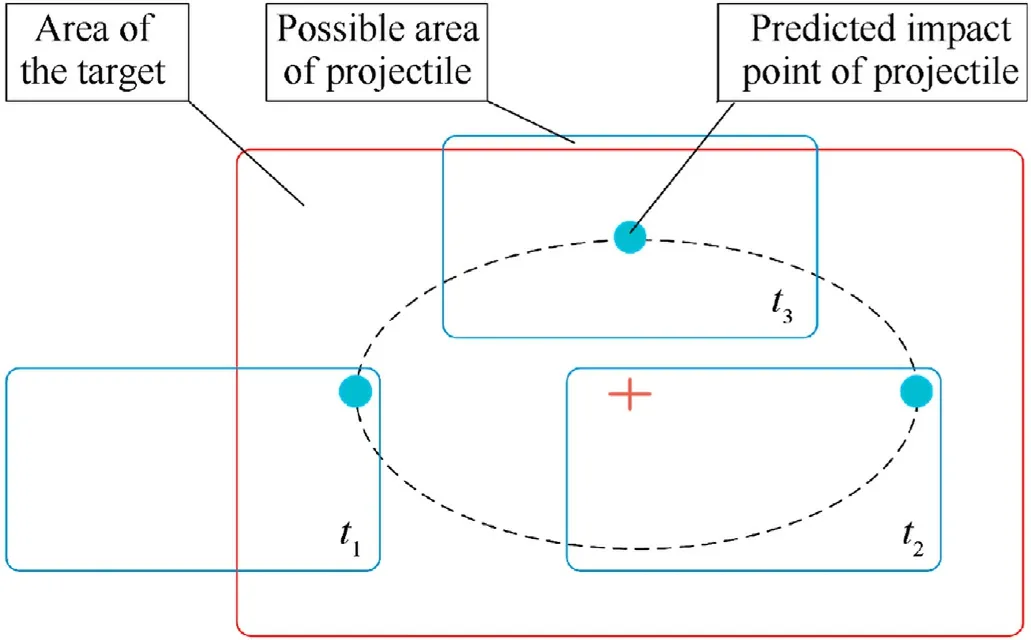
Fig.6.Description of projectile-target intersection.

According to Weierstrass theory, any continuous function in a closed interval can be the optimal and uniform approximation by polynomial series.The CPE is constructed as follows.

Forx∈［a，b］, a one-dimensional Chebyshev series of orderkis defined as follows:

While the Chebyshev series is expressed as a polynomial,there is the following recurrence relation:

For multidimensional problems,n-dimensional Chebyshev polynomials are defined in x∈［-1，1］nas the tensor product of n one-dimensional Chebyshev polynomials, as shown below:

wherefrepresents the coefficient of Chebyshev polynomials.lis the number of 0 contained ini1，i2，…，in.According to the orthogonality of Chebyshev polynomials,the coefficientcan be obtained by integral.

By using Mehler integrals to solve Eq.(45), it can be obtained that

wherexjis the interpolation point of the numerical integration,which is calculated as follows:

Remark.Through the above process, the CPE of the EB-ODE is constructed, to improve the speed for the prediction of projectiletarget intersection.For the constructed CPE, the upper and lower boundaries of the EB output response will be obtained by interval UNA method.

5.3.The interval uncertainty analysis method based on affine arithmetic

Assuming that the inputxis affected by multiple uncertainty factors, which can be regarded as noise signals, then thexcan be written as affine form Refs.[48,49].

wherex0is the central value of,xiis partial deviations, and εi∈［-1，1］ is noise symbol which is unique noise.εirepresents different noise, and different noise units are independent of each other.Therefore,|εi| =1,xobtains its upper and lower bounds,that is

Remark.The uncertain variablexcan be converted into interval form by Eq.(49).If the expression of the same noise unit appears in two or more affine forms, it indicates that their uncertainties are related to each other.

The simple affine form of multiplication is as follows:

The error of this method is very large,and more accurate range analysis results can be obtained by using Chebyshev approximation[38,40,50].The Chebyshev affine form of multiplication is

in which εr+1is a new noise element introduced by Chebyshev approximation.α，β are the approximate maximum and minimum in, respectively.

Remark.Since the CPE of EB-ODE only has multiplication and addition operations, only the multiplication of Chebyshev affine is given here.

According to the AA, the uncertainty variablexiin the EB-ODE can be expressed as=xi0+ Δxi·εi, wherexi0is the interval median and Δxiis the interval radius.Then the CPE of EB-ODE can be rewritten into the affine form.

wherediis a function of x.Therefore,the interval response of the EB dynamics model affected by uncertain variables can be obtained.

Remark.The main purpose of the interval UNA of the EB-ODE is to obtain the interval boundary of the impact area of the projectile.After UNA, the projectile coordinates of the return control system are

6.Co-simulation

6.1.Virtual prototype model of multi-body system dynamics

According to the topology in Fig.7, the multi-body system dynamics model of moving tank is constructed in Recurdyn (multibody system dynamics software).The main structure includes road,track,hull,turret,and artillery.A 3-D road model is established by harmonic superposition method [51-53].The final multi-body system dynamic model of moving tank is shown in Fig.8.

Remark.It can be noticed that the shape of the turret and barrel is irregular and the density is not uniform.Therefore,it is regarded here as the uncertainty of the model,such as ΔM,ΔCand ΔGin Eq.(26).Moreover, the uncertain disturbanceF（t） in Eq.(9) will be provided by random roads.

6.2.Co-simulation model

Fig.7.The topokogy of moving tank.

Fig.8.The multi-body system dynamic model of moving tank.

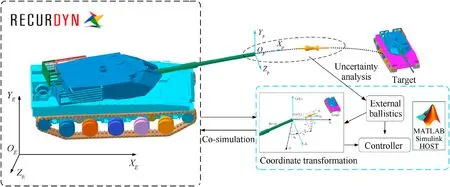
Fig.9.The logic diagram of the co-simulation.

The numerical simulation model of control system (including EB)is established in MATLAB/Simulink software.The data exchange between the control system and the mechanical system is realized by using the interface between RecurDyn and MATLAB/Simulink,thus co-simulation is realized.Fig.9 shows the logic diagram of cosimulation.

6.3.Simulation parameter selection

The speed of the tank is 20 km/h, 30 km/h and 40 km/h respectively on the E-class road,and it accelerates to a steady state in 2 s.The moving target is 2000 m away from our tank and is driving at a constant speed of 30 km/h,as shown in Fig.10.In line with the international military standard, the size of the moving target is 4.6× 2.5 m2.

The structural parameters in Eqs.(7)and (8)are consistent with the virtual prototype model, which is set tom1=5200 kg，m2=2088 kg，L1=1.05 m，L2=5.12 m，g=8.8 m/s2.To clarify the effect of proposed control strategy,the classical linear controller PID which is not based on the model is used as the comparison.The PID controller are set tokp1=201ki1=11.2kd1=1.5 andkp1=45ki1= 5.1kd1= 1.3.

To meet the Assumption 2, let

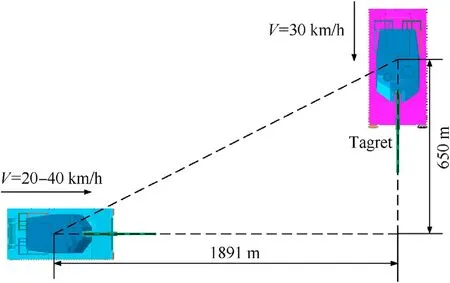
Fig.10.The initial state of simulation.

The controller parameter is set tol1=l2= 5,κ = 150,k1= 5,ε = 0.01,P= 5.1.

The initial velocity v（t）, swinging angle Ω1，2（t） and swinging angular velocityof projectile in the EB-ODE are selected as the interval uncertainty parameters, and the range is selected as shown in Table 1.The wind speedwx，z（t）=1+sin（10πt） （m/s）are random parameters.The schematic diagram of EB interval UNA under 7.5°firing angle and 1000 m firing distance is given in Fig.11.As shown in Fig.11,the shaded area is the range of possible impactpoints of projectile in the current firing state, and a comparison is given to directly solve the differential equation with the Runge-Kuda methods (ODE4-5).Compared with ODE45, the interval range solved by this method still has a certain wrapping effect[32].There are 30 sample points in Fig.11, and Table 2 shows the maximum and average error of these sample points.The maximum error in both directions is only 1.54 cm,and the average error is less than 1 cm, indicating that the accuracy of proposed method can meet the requirement for the prediction of projectile-target intersection.

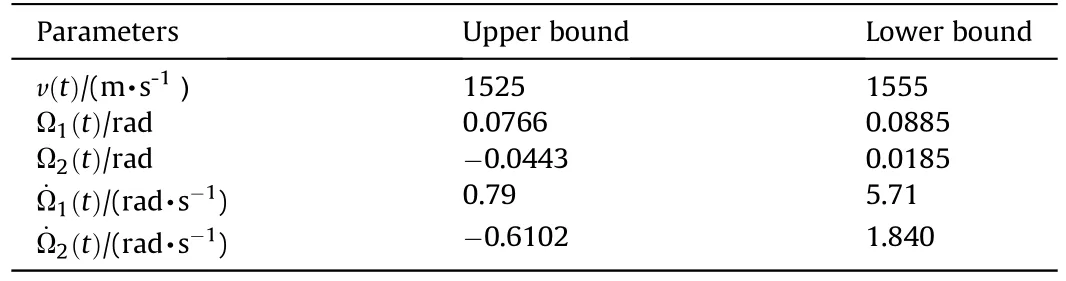
Table 1The range of interval uncertain parameters in EB-ODE.

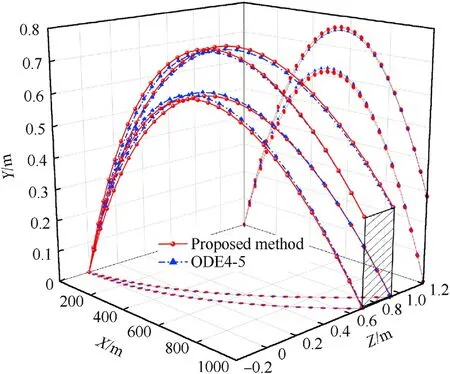
Fig.11.Schematic diagram of EB-ODE with interval UNA.

Table 2The error of UNA.

Remark.Before the UNA, these interval uncertain parameters are added to the control process in the form of random numbers.After UNA,only the wind speed are uncertain parameters in the EBODE.

7.Results analysis

The prediction accuracy of projectile-target intersection can be expressed by the average value of the absolute error between the coordinates of the projectile impact points coordinates and target points.

where,Nis the number of sample and ΔXiis the coordinate error.

Remark.According to the 6σ principle, the prediction accuracy δY＜0.42 m and δZ＜0.77 m in the vertical and horizontal direction respectively, which can meet the requirement of prediction accuracy.

7.1.Comparison of prediction results of projectile-target intersection

Fig.12 shows the dynamic comparison of the prediction error before and after using the UNA on the condition of speed 40 km/h.The control trend of the two curves is almost the same and can approach the target after acceleration completion.However,under the influence of uncertain parameters, the control effect jitters violently and the stability of the system is poor without UNA.

Table 3 lists the prediction accuracy, error extremum and standard deviation after control stability in the two situations.The error extremum in both vertical situations are less than 1.25 m,and the prediction accuracy is less than 0.42 m.In the horizontal direction,the error extremum without UNA has exceeded 2.3 m.After using UNA, the prediction accuracy of vertical and horizontal direction is improved by 83.5% and 17.6% respectively, so that it can still meet the prediction accuracy on high-speed conditions.From the standard deviation of coordinate error,the random disturbance caused by uncertainty has a great influence on the system.

Fig.13 shows the history of adaptive parameter.The adaptive parameterin both situations can reach steady state before 2 s.After the uncertainty analysis, the peak value of the adaptive parameterhas decreased,and the jitter is smoother in the steady state, which shows that the uncertainty level of the system has decreased.

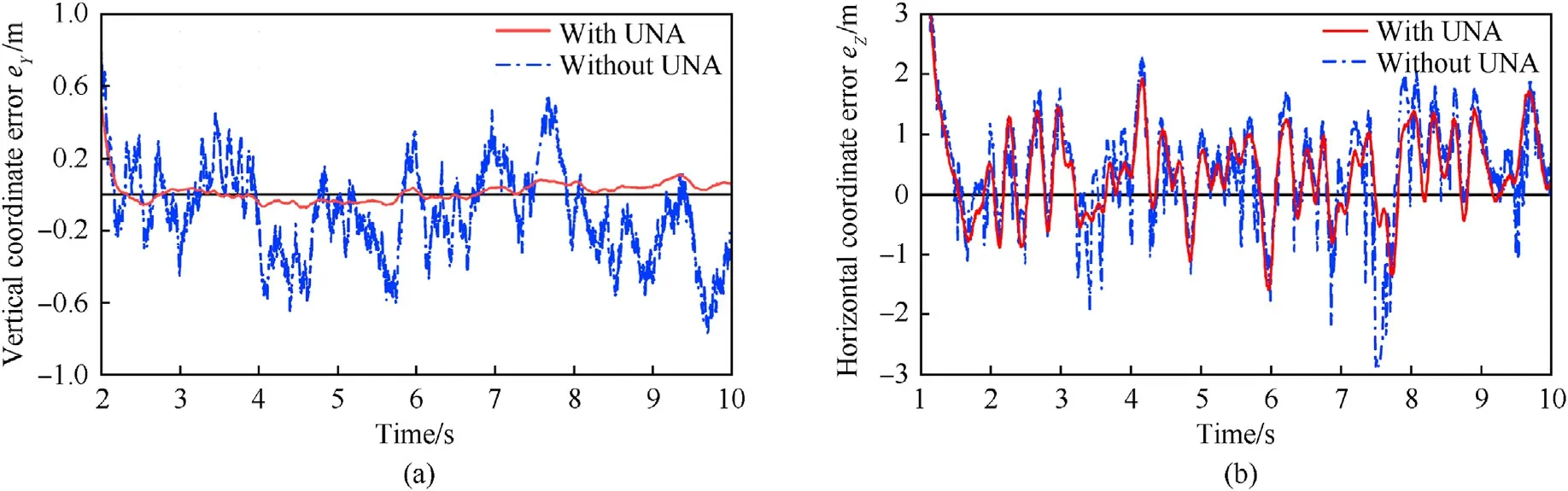
Fig.12.Comparison of coordinate error before and after UNA: (a) Vertical error; (b) Horizontal error.

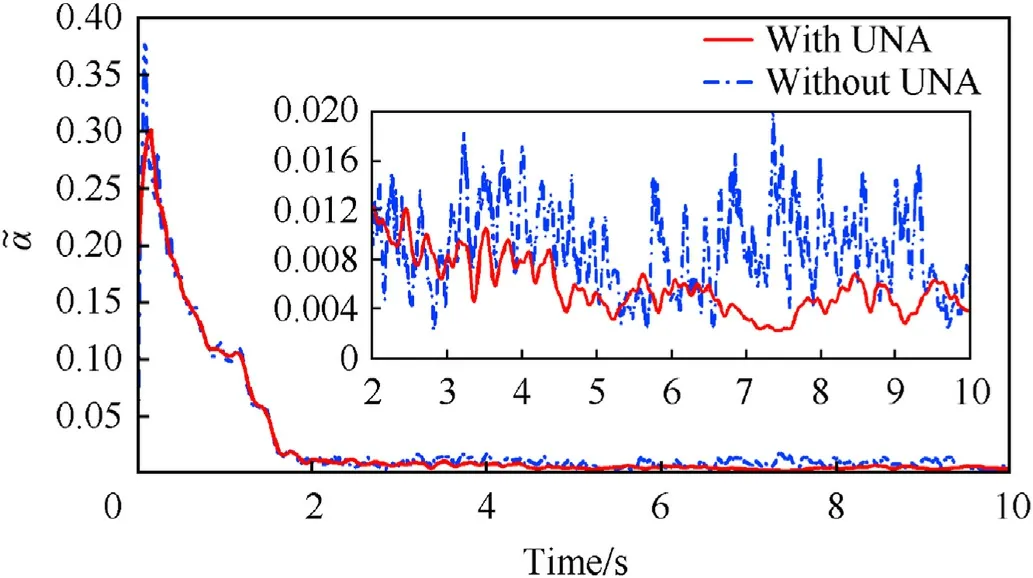
Fig.13.The history of adaptive parameter .

Table 3The coordinate error(m) before and after UNA.

To further verify the effectiveness of proposed method, the firing state (firing angle, firing distance) at different moments(sampling time interval is 10 ms)in the stable state is selected,and the impact of 10 projectiles is simulated at each moment.The optimal Latin hypercube design(OLHD)is used to extract 10 sets of data in the interval of uncertain parameters, and the calculated results are shown in Fig.14.The projectile dispersion with UNA is smaller and more uniform.The hit probability without UNA is 88.39%and the hit probability with UNA is 96.55%,which increases by 9.2%.

7.2.Controller comparison

Figs.15-17 show the comparison of dynamic error between the proposed control (with UNA) and PID control (with UNA) at different speeds (20, 30, 40 km/h).It can be seen from the figures that under proposed control, the stability system can track the target within 2 s,while the tracking speed of PID control is slower.The prediction accuracy and error extremum of the two controllers in steady state are listed in Table 4.The vertical error of the two controllers is very small and can meet the prediction requirements.

Fig.14.The projectile dispersion: (a) Without UNA; (b) With UNA.

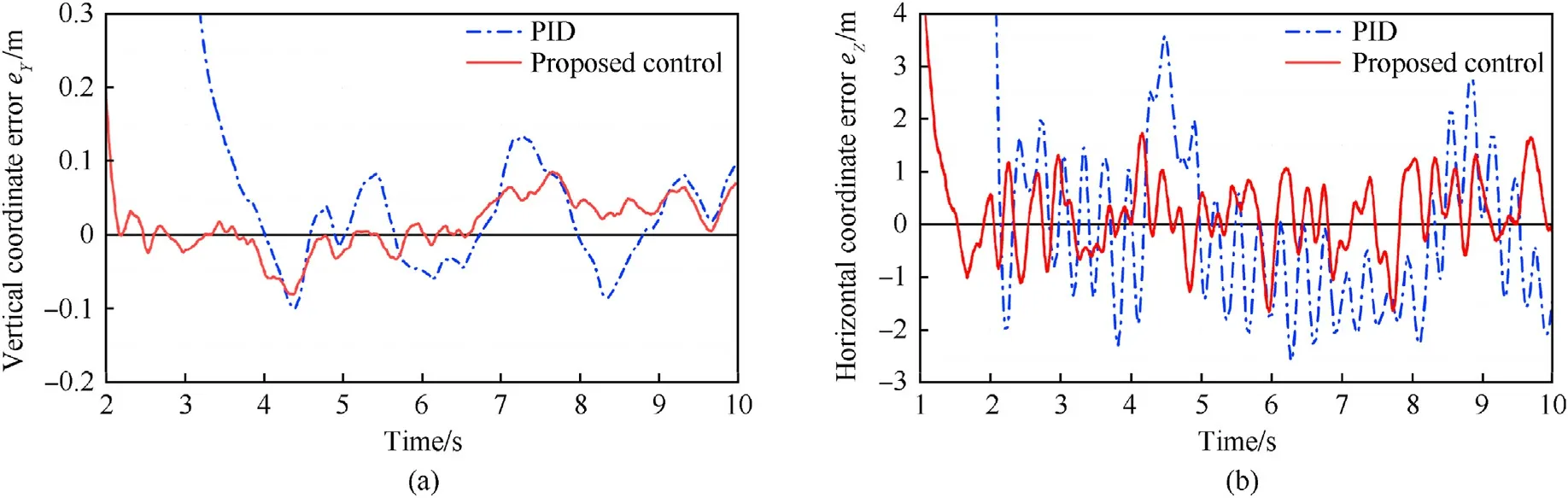
Fig.16.Comparison of coordinate error at 30 km/h speed: (a) Vertical error; (b) Horizontal error.

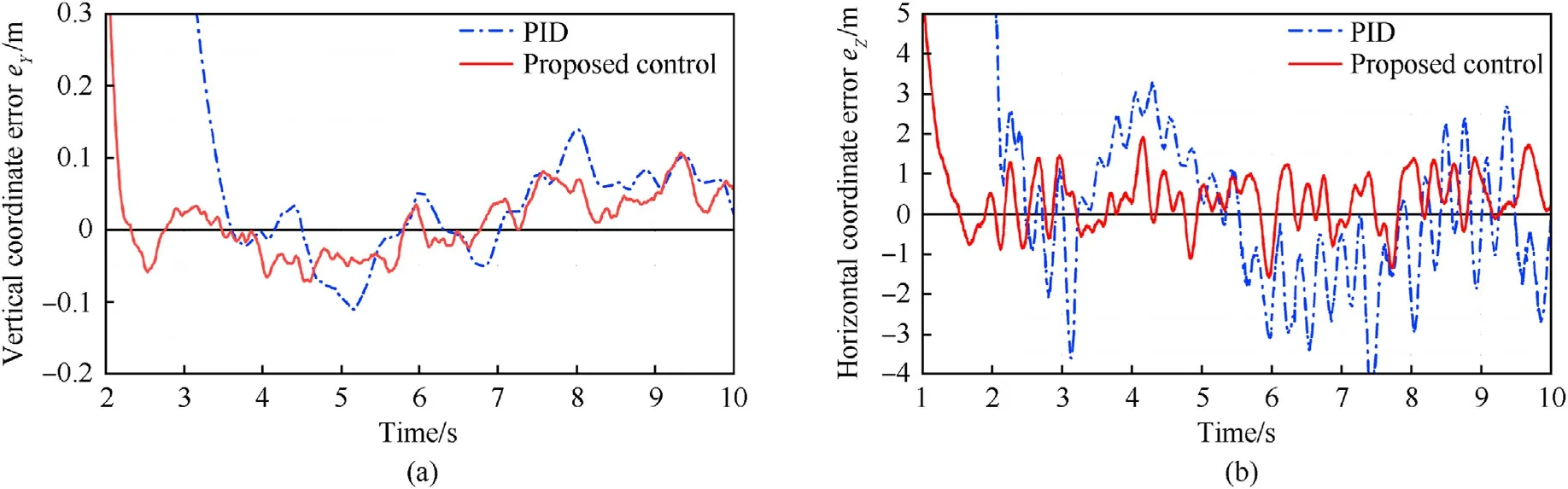
Fig.17.Comparison of coordinate error at 40 km/h speed: (a) Vertical error; (b) Horizontal error.

Table 4The coordinate error(m) at different speeds.

However,in the horizontal direction,the error extremum of PID control has all exceeded 2.3 m, and the prediction accuracy has exceeded 0.77 m, which has been unable to meet the prediction requirements.Meanwhile,the prediction accuracy of the proposed control is still less than 0.77 m at 40 km/h speed.With the increase of tank speed, compared with the PID, the horizontal prediction accuracy of proposed control increased by 41.44%, 54.11% and 57.52%respectively,and the error extremums decreased by 25.52%,51.86%and 59.61%,respectively.Hance,with the increase of level of uncertainty, the performance of proposed control is more stable,and it can effectively restrain the impact of uncertainty (system modeling error, external disturbance, etc.), and can still meet the prediction accuracy under high-speed conditions.

8.Conclusions

This paper mainly focuses on the stability control problem for the prediction of projectile-target intersection of moving tank.It is expected that the hit probability of tank can be improved by means of stability control and uncertainty analysis.First, aiming at the problem of stability control and prediction of projectile-target intersection for moving tank, an adaptive robust constraintfollowing controller based on U-K theory is designed.The EBODE with uncertainties is integrated into the bidirectional stability system of tank so that the problem of projectile's impact-point control is transformed into angle control, which realizes the realtime prediction of projectile-target intersection.Then, in view of the uncertainty of EB-ODE, the interval UNA method which combines the CPE and AA is adopted to transform the uncertainty problem of projectile-target intersection into a deterministic problem.Finally, to verify the effectiveness of proposed method,the control model is established in MATLAB/Simulink, and the multi-body system dynamics model of moving tank is established in RecurDyn.The co-simulation results demonstrate that the proposed method can effectively improve the prediction accuracy of moving tank.On the 40 km/h and E-class road conditions, the hit probability of moving tank has been increased by 9.2% with UNA.Compared with PID control, it is verified that the adaptive robust constraint-following control can converge and reach the stable state quickly,and can effectively restrain the uncertain factors such as system modeling error and road excitation.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was financially supported by the National Natural Science Foundation of China (Grant 52175099), the China Postdoctoral Science Foundation(Grant No.2020M671494),the Jiangsu Planned Projects for Postdoctoral Research Funds (Grant No.2020Z179), the Nanjing University of Science and Technology Independent Research Program(Grant No.30920021105).