Cooperative UAV search strategy based on DMPC-AACO algorithm in restricted communication scenarios

Shiyun Chi , Zhen Yng ,b,*, Jihun Hung , Xioyng Li , Yiyng Zho ,Deyun Zhou

a School of Electronics and Information, Northwestern Polytechnical University, Xi'an 710072, China

b School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

c The 93147th Unit of Chinese PLA Air Force, Chengdu, 610091, China

Keywords: Unmanned aerial vehicles (UAV)Cooperative search Restricted communication Mission planning DMPC-AACO

ABSTRACT Improvement of integrated battlefield situational awareness in complex environments involving dynamic factors such as restricted communications and electromagnetic interference (EMI) has become a contentious research problem.In certain mission environments, due to the impact of many interference sources on real-time communication or mission requirements such as the need to implement communication regulations, the mission stages are represented as a dynamic combination of several communication-available and communication-unavailable stages.Furthermore, the data interaction between unmanned aerial vehicles (UAVs) can only be performed in specific communication-available stages.Traditional cooperative search algorithms cannot handle such situations well.To solve this problem, this study constructed a distributed model predictive control (DMPC) architecture for a collaborative control of UAVs and used the Voronoi diagram generation method to re-plan the search areas of all UAVs in real time to avoid repetition of search areas and UAV collisions while improving the search efficiency and safety factor.An attention mechanism ant-colony optimization(AACO)algorithm is proposed for UAV search-control decision planning.The search strategy is adaptively updated by introducing an attention mechanism for regular instruction information, a priori information, and emergent information of the mission to satisfy different search expectations to the maximum extent.Simulation results show that the proposed algorithm achieves better search performance than traditional algorithms in restricted communication constraint scenarios.

1.Introduction

With the rapid development of unmanned aerial vehicle (UAV)body performance, functional flexibility, and autonomous control related technologies,UAVs have been widely used in fields such as battlefield identification and ground target strikes, forest fire site search, and monitoring of live animals in nature reserves [1,2].Compared to single UAV, multiple UAVs can perform complex search missions more effectively and improve the robustness and flexibility of the entire UAV platform [3-6].Therefore, a large amount of research is devoted to UAV cooperative search.

Common cooperative search algorithms mainly include: (1)probability sampling-based algorithms [7,8], (2) geometric algorithms[9],and(3)Intelligent algorithms[10-12].With the increase in the problem scale, probability sampling-based algorithms featured an exponential increase in computation and a lack of the capability when facing complex scenarios, whereas geometric algorithms, such as parallel sequence search (PSS) [13,14], need to plan the search paths in advance and exhibit poor flexibility.Because of its superiority in handling complex NP problems[12,15],intelligent algorithms are being increasingly applied to UAV cooperative search problems.Previous studies [8,16,17] have adopted intelligent algorithms such as heuristic algorithm for cooperative search missions and [18] hybrid evolutionary algorithm to solve human-machine collaborative-search planning missions.The abovementioned studies work well in solving UAV search planning;however,because they all adopt a centralized control architecture,such as in Ref.[19], there is a decision unit responsible for processing the data of all UAVs, performing mission plans, and distributing the planning results to other UAVs.The decision unit is more conducive to finding a global better solution because it obtains the data of all UAVs in the cluster;However,owing to the need to handle all UAVs’ data, the algorithm calculations are large and time consuming.When a UAV cluster encounters an emergency,requiring a re-planning,a large amount of data may cause decision lags, and the flexibility of cluster is poor.Simultaneously, with a centralized architecture, decision-making requires the acquisition of the entire information of a UAV cluster, which is highly dependent on the communication data link transmission rate index and real-time performance index.When faced with electromagnetic interference (EMI), a UAV cluster loses mission execution ability due to the lack of decision-making information.Therefore,designing a distributed algorithm that can adapt to the evercomplex communication environment and improve the overall efficiency of searching for targets is requirement, and is the prime objective of this paper.

Among the search-planning algorithms that employ a distributed control framework, traditional cooperative UAV search algorithms based on distributed architectures often need to perform mission partitioning before mission execution via manual assignments or simple automated strategies,such as the cooperative PSS algorithm[13,14].In previous studies[20-23],each unit in a cluster planned a search path according to its own best search capability.Although distributed control was realized,a lack of data interaction and cooperation within a cluster reduced the search efficiency of the entire cluster.A study [11] used a Bayesian network search graph-generation method combined with a particle swarm optimization(PSO)algorithm to improve the search efficiency in largescale scenarios.Another study [20] used a distributed architecture wherein each UAV in a cluster used an improved ant-colony optimization (ACO) algorithm for local optimization and finally completed the information interaction within the cluster through a data link to obtain an optimal decision for the cooperative search.Although these algorithms solved the cooperative search problem of multiple UAVs in a distributed architecture, they were highly dependent on the availability of the data link.Furthermore, when the communication was interrupted or the mission required communication silence, the planning of the search task could not be completed due to their inabilities to interact with the data,which caused the search area of each UAV to be repeated,and even some tracks overlapped leading to collision losses.Aiming at this problem,a study[24]was conducted to guarantee the accuracy of a data link that could obtain interactive information by considering the complex environment interference when the data link was not stable.In terms of data-link loss, Lili [24] used an improved least square method (LSM) to compensate the loss of information by introducing a target location model fitting function that could improve the data-fitting precision.This algorithm ensured the cooperative search missions of UAVs in during EMI.However,although the problem of data loss was considered in these studies,the data link could maintain normal communication during the entire task process.With increasing complexity of search mission scenarios,the radio frequency(RF)environment in various current scenarios is complex,and there are many interference sources in a mission.During mission execution, communication can often be completed only within a specific time,and data interaction cannot be carried out in non-specified times.Solving the problem of the availability of communication discontinuities is the second objective of this study.

For solving the UAV cluster search problem in complex electromagnetic environments where data interactions are available only at specific times, inspired by the mathematical properties of Voronoi diagrams [16,25], this study proposes an algorithm.The proposed algorithm is based on a distributed architecture with ACO combined with Voronoi diagrams, considering the effect of intermittent communication on data interactions in distributed architecture clusters.

The main objectives of this study are as follows.(1) In view of the limitation of interrupted communication, the region division method of Voronoi diagrams is adopted to solve the problem that UAVs exhibit in each region during the search process in complex scenarios.When communication is available, data exchange is performed inside a UAV cluster,and the search areas of these UAVs are re-planned in real time according to the current situation information.Simultaneously, the problem of collision loss and repeated searching caused by the UAV cluster's inability to interact with their respective positions in real time is solved.(2) A distributed model predictive control (DMPC) framework based on Voronoi diagrams is proposed to solve the problems of data interaction and control optimization of UAVs.(3) For the UAV search-control planning problem, when no real-time global information can be used to optimize the solution of the task assignment and considering the limited search range of a UAV and the requirement of realtime processing, an attention mechanism ant-colony (AACO) algorithm is proposed.According to the characteristics of a UAV search mission, to enhance the search efficiency of ACO during a search, a search factor to strengthen the search effectiveness of UAVs in the unsearched areas and to accelerate the algorithm convergence is proposed.

The remainder of this paper is organized as follows.Section 2 describes the problem and the development of the mission model of UAV cooperative search.Section 3 presents the proposed DMPCAACO algorithm based on the Voronoi diagram partitioning method.Section 4 presents the simulation results.Finally,section 5 provides the conclusions.

2.Model and problem description

2.1.Mission description

Battlefield environment is complex and changeable.In a cooperative search mission, UAVs carrying detection equipment are assumed to form a group to conduct coverage search in a specific complex-task area,and there are several key areas that need to be searched first.Due to a complex electromagnetic environment in the mission area, the high-speed data link of each unit in the UAV cluster experiences interference; therefore, real-time data interaction cannot be completed, and communication can only be performed at specific periods.The UAV cluster searches the key area according to the real-time planning path, and subsequently, completes the coverage search of the entire mission area.During the search process, its own information and the that of the search are shared within the UAV cluster in the limited time window of communication to achieve the maximum search effectiveness.

A cooperative search idea diagram of multiple UAVs is shown in Fig.1.To solve the cooperative search mission-planning problem of multiple UAVs, a few assumptions were made as follows.

(1) Mission area can be expressed as Environment =.It is a matrix region with length and width asLxandLy,respectively[26],where（x，y）indicates the cell inith row andjth column.

(2) There are single or multiple uncertain regions with prior probabilities in the mission area,the position of targetNtcan be expressed as follows:

Fig.1.Battlefield environment.

(3) The optimization goal is to minimize the average environment uncertainty [19] of the entire mission area and maximize the search coverage of themission area.

2.2.Model of UAV

The state of a UAVUiin timetis

The current position of a UAV is expressed as follows:

The current course information of UAV is expressed as follows:

In Eq.(4),the UAV is currently in a flight state and heading,and in the next moment,it can use a limited angle of heading.According to the maneuverability of the UAV, the available headinghcan be set between 1 and 7 corresponding to the positive front,right front 45°,positive right,right back 135°,left back 135°,positive left,and left front 45°heading angles, respectively, as shown in Fig.2.

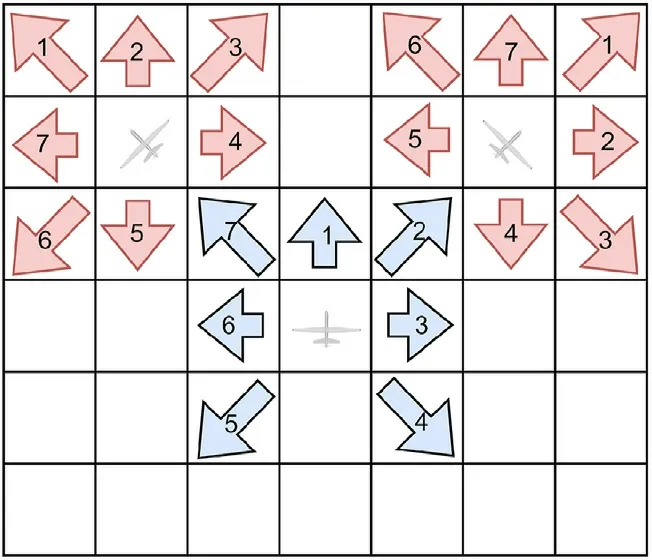
Fig.2.Course limitation of UAV.

2.3.Model of airborne sensor

The search efficiency of an airborne sensor carried by a UAV is represented as

whererrepresents the distance between the detected position and the current position of the UAV andPdrepresents the maximum detection efficiency of the UAV.In other words,fMAX=pd, whenr→∞andf→0.However,because of the reliability constraint, the trusted detection range is limited,that is,rtakes a finite value.Here α is an adjustable parameter for differentiating the detection performance of different sensors at different distances.As the rasterized scenario was used in this study,the detection efficiency was discretized to obtain the average detection efficiency in the cells,such that the same detection efficiency was obtained in same cells.Therefore,the detection efficiencyF（r）of a cell with a distanceRis expressed in Eq.(6).The change in efficiency trend is shown in Fig.3.With the increase in detection distance,detection efficiency gradually decreased.

2.4.Uncertainty of environment

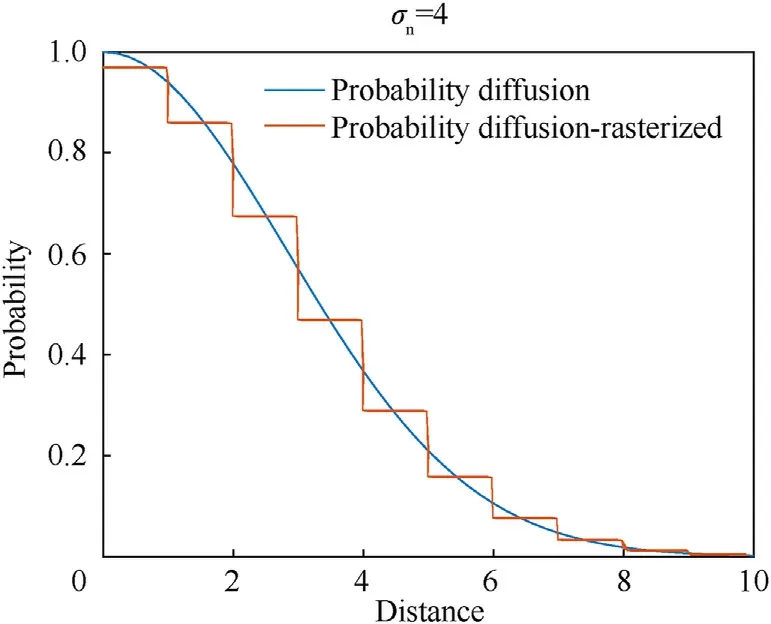
Fig.3.Detection efficiency of sensors at different distances.

To express the degree of search of the mission area and quantify the multi-UAV cooperative search index, we introduced the environmental probability map and the concept of uncertainty[19].In a real environment, the existence and distribution of targets are unknown.Each cell （x，y） has a certain probability of existence of targets,which constitutes the target probability map of the mission area.Here, an initial value of environment uncertaintyPinitialwas set for the entire mission area based on a priori information before the task execution started.Therefore, the probability that a target exists in the mission area att=0 wasP（x，y，t0） =Pinitial.

The environmental uncertainty χ（x，y，t） indicates the knowledge of the UAV cluster regarding the environmental situation information in cell（x，y）att,where χ（x，y，t）∈［0，1］.Here,χ（x，y，t）=1 indicates that the UAV is completely uncertain about the situational information contained in the cell, and χ（x，y，t）=0 indicates that the UAV completely understands the situational information of the cell.In an actual mission execution, this will be based on a priori knowledge.In other words,if a threshold χthresholdis set,and when χ（x，y，t）＜χthreshold,the search degree of the cell（x，y）is considered to have met the expectation.The aim of the cooperative UAV search mission is to decrease the environment uncertainty of the entire mission area in a more efficient manner by employing the derived search strategy for the entire UAV formation, such that the probability density map is transformed during the execution of the search mission to obtain an uncertainty information map of the mission area.The environment uncertainty of cell （x，y） attis

whereP（x，y，t） denotes the probability of existence of a target in cell （x，y） att.Therefore, the uncertainty χ（x，y，t） varies with the probability densityP（x，y，t）curve, as shown in Fig.4.

3.Cooperative searching algorithm

In complex mission environments, owing to the influence of interference sources on real-time communication or mission requirements, such as a need for radio control, mission phases are represented as several communication-available phases and communication-unavailable phases, that is, the communication and non-communication windows, such that the internal data interaction within a UAV cluster is available only in specific communication windows.Here, the Voronoi diagram generation method was used to plan the mission area, and AACO was used to complete the search of each UAV under the distributed model predictive control architecture.The framework is shown in Fig.5.

3.1.Division of UAVs cooperative search areas based on Voronoi diagram

Fig.5.Structure of algorithm.

We assumed that there areNuUAVs that cooperate to search a mission area.Moreover, there are a few mission scenario limitations such as uncertainty in the locations of targets in the target area,interference in the target area,and intermittent availability of the data link.Due to these limitations, the UAVs were required to complete the area search during the non-communication period and avoid collision or searching the same area simultaneously.The Voronoi diagrams contain many excellent spatial generalization properties, such as proximity and neighborhood, and are commonly used in UAV path planning[27].A Voronoi diagram is an equidistant convenient distance division method.TheNuUAVs located in the mission area are regarded as sites labeled asP= ｛p1，p2，…，pNu｝, and a Delaunay-triangle network was constructed according to these sites.According to the point set of the intersection of the lines connecting the perpendicular bisectors of the sides of each triangle in this network, considering the nature of the perpendicular bisector, each point in the point set was the circumcenter of the corresponding Delaunay triangles.These circumcenters were connected to obtain the Voronoi diagramVor（P）corresponding to the point setP,as shown in Fig.6(c).The Voronoi diagram divided the mission area intoncells, denoted asV（pi）.Considering the points inV（p4） as an example, the Euclidean distance between any pointqwithinV（p4）in Fig.6(c)and a cluster of four UAVs can be expressed as

Asqlies withinV（p4）, according to the nature of the vertical bisector, when and only when for ∃pj∈P，（j≠i）, all havedist（q，pi）＜dist（q，pj）.For any pointqin the search areaV（pi）divided for UAVi,UAViis closer to it than other UAVs and has a greater distance advantage when searching for this point, thereby obtaining the optimal division scheme at that time.Furthermore, when communication is not available, each UAV searches within its correspondingV（pi）, avoiding the collision problem caused by the failure to obtain the position of the friendly aircraft in real time.The generation process is presented in Algorithm 1, and the process schematic is illustrated in Fig.6.

3.2.Framework based on DMPC

Based on a DMPC framework[13],the search-mission planning problem of a full mission cycle was converted to a short timedomain planning problem.The planning strategy could be adjusted in real time during the communication-available phases,and a DMPC framework based on Voronoi diagram was established.Considering all UAVs performing a mission as a large system, the UAV state of the system wasX（t）=｛X1（t），X2（t），…，Xn（t）｝ and the input of control for the system wasU（t） = ｛U1（t），U2（t），…，Un（t）｝.Therefore the state equation of the entire cooperative system can be expressed as

Fig.6.Area division process based on Voronoi diagram.

wheref（）is the state transfer function of the UAV system,and the state Statei（t） of the UAViis Xi（t） = ［pi（t），hi（t）］T, wherepi（t）=（x，y） indicates the current position of the UAViandhi（t） indicates the current heading of the UAVi.HereUi（t）=［Δhi（t）］is the input of control for the UAVi,and Δhi（t）indicates the next forward direction of the UAVi.

Within the search area, the equations of the state of the UAVican be expressed as

whereF（pi（t），hi（t）） represents the change in the moving coordinates of UAViwhen execute the variation of coursehi（t）, andYawi（t+1） represents the course of UAViin the northeast coordinate system.Thehi（t）corresponding course angles of values 1 to 7 in Eq.(4) are ｛- 135°， - 90°， - 45°，0°，45°，90°，135°｝.The schematic of course limitation of UAV is shown in Fig.2.

The objective of the multi-UAV cooperative search was to reduce the environmental uncertainties in the mission area to the maximum extent; therefore, the optimization objective function was described using the search effectiveness functionJ（t）.Here,J（t）is a combinatorial function comprising the gainJχ（t） from the decrease in environmental uncertainty, the gainJD（t） from detecting the undetected region, and the gain functionJE（t） from detecting the desired detection region, as expressed in the following equations:

where ω1，ω2，ω3denote the weights corresponding to the three gain functions, and ω1+ ω2+ ω3= 1.Here,detectedMap（x，y） denotes the search representation,and whendetectedMap（x，y） = 1,it indicates that cell （x，y） has been searched, and whendetectedMap（x，y） = 0, it indicates that cell （x，y） has not been searched.Furthermore, ExceptedArea represents the desired search area.

In the framework of the distributed system, the entire system comprised several independent UAVs, that is, different UAVs distributed in the battlefield were controlled independently,different UAVs were connected only through the data link, and all UAVs exchanged information and coordinated with each other.For such a large system composed of multiple independent dynamic subsystems,an MPC controller existed in each individual UAV that processed and interacted with the information of other UAVs obtained from the data link and completed the coordinated interaction of the entire large system.Due to the independence of each UAV,the state equations of the UAV search system can be expressed as

In summary, the entire system attp1, the decision moment,returned an objective function, which can be expressed as

whereXi（tp1）is the predicted state andUi（tp1） is predicted control of UAViattp1moment,derived from the MPC of each UAV,｛Xj（tp1）｝denotes the state of input,and｛Uj（tp1）｝denotes the control input of all UAVs except UAVi.

Therefore, for each independent UAV in the large system, the predictive control of its local MPC and AACO can be expressed as follows:

whereXi（tp1） is the sequence that represents the current and predicted states of UAVi,Ui（tp1） represents the predicted control sequence of UAVi,and the goal of programming algorithm AACO is used to provide the appropriateUi（tp1）, such that the predicted control sequence of UAVi, is obtained at timeTp.Its algorithm is presented in Algorithm 2.

As shown in Fig.7,Tprepresents the prediction step of the UAV,TCrepresents the execution control steps of the UAV, andtpirepresents the start time of the UAV execution prediction.Furthermore, at each decision momenttp1, each UAV uses the AACO algorithm to solve for the optimal search withinTptime-step trajectory,and interacts via the MPC module to make another decision attp2=tp1+Tcto ensure that the UAV is executing the optimal decision planning in the current time step in each execution period.

3.3.ACO based on attention mechanism

In nature,ants leave pheromones during exploration and guide other ants to finish foraging through pheromone volatilization and aggravation.Similarly, the ACO algorithm is a swarm intelligence optimization algorithm, simulating the foraging behavior of ants[28-30],with high robustness and environmental adaptability and is widely used in path-planning problems.Traditional ACO algorithm obtains the better search paths by trial and error in the first stage,which has slow convergence speed and blindness.To address this problem, an attention mechanism ACO for search planning of each UAV under DMPC framework is proposed, to efficiently complete the UAV cooperative search mission.According to the characteristics of a search mission, the target probability map and environment uncertainty map χ（x，y，t） are processed by the attention mechanism, which in turn affects the gain of the ACO under different search paths, i.e., Eq.(11), and guides the UAVs to perform the cooperative search missions.

In a cooperative search mission, there are often one or more regions in the mission area that have the probability of the existence of the target, which are detected by other methods in advance,and these regions need to be searched on a priority basis.When unexpected events occur in some areas, emergency search and detection is required.For such problems, an attention mechanism is proposed based on the attention points to process the pheromone matrix.The attention points were divided into three types for three situations: significant concerns, emergency concerns and normal concerns.Furthermore, based on these three concerns to guide the search, the search efficiency was improved.

(1) Significant concerns

In a cooperative search mission,a certain location in the mission area often exhibits prior probability obtained using a satellite,ground investigators, and other investigative techniques, and the mission requires priority investigation of these locations.For these special mission areas, the concept of significant concerns was added to the proposed attention mechanism.When the prior probabilityPprior（xn，yn） exists in a cell （xn，yn） of the significant concernsn, the peak of Gaussian distribution function is used to initialize the target existence probabilityPprior（xn，yn）, where the possible location of the target is the center of the peak of the Gaussian distribution.Therefore, the initial moment target probability density function can be expressed as

wheref｛（x，y，t0）|（xn，yn）｝is the diffusion probability density of the significant concerns in cell （x，y） att0and σ2nis used to control the probability density diffusion range of the significant concerns,which indicates the probability peak width of the target.And diffusion effects under different σ2nare shown in Fig.8, corresponding to the detection ranges of different detectors.

(2) Emergency concerns

Fig.7.Structure of DMPC based on AACO and Voronoi diagram.

Fig.8.Probability density diffusion results of significant concerns for different values of σn

When an emergency occurs in the search area, the UAV in a cluster is required to perform a search mission for the location of the emergency.For determining the location of emergency concerns,it is possible to confirm that the current location（xe，ye）has an unknown event at the current timete; Therefore, it can be considered that the environmental uncertainty here increases to 1,that is,χ（xe，ye，te） =1.Therefore,the UAV cluster cannot determine whether the sudden unknown target is a fixed target or a moving target.If it is a moving target, then the target speed, size, and direction are unknowns.Therefore,the following assumptions can be made:

(a) The target position remains independent in thexandydirections.

(b) The target acceleration remains constant at each time step Δt,which is a Gaussian white noise sequence with the same variance.

(c) The magnitude and direction of the target velocity are independent of each other and obey Gaussian distribution.

If the above assumptions are satisfied, the motion of the target can be considered to follow the two-dimensional standard normal distributionof initial position （xe，ye）, and the probability density function of cell （x，y） in the diffusion region can be expressed as

(3) Normal concerns

When the two special concerns mentioned above do not exist in the planned mission of a UAV cluster, the normal concern plays a role in guiding the UAVs to conduct a coverage search of the entire mission area.In this study, the concept of centroid of uncertainty[31]was introduced to generate the common concerns to guide the UAVs to finish a mission.In the case of divided Voronoi diagram region, assuming that the Voronoi diagram region of the UAViat the current timet0isV（pi）, and there arencells, with coordinates（x1，y1），（x2，y2），…，（xn，yn）for their centers,then the uncertainty of each cell is used to represent the mass χ（x1，y1，t0），χ（x2，y2，t0），…，χ（xn，yn，t0）.Subsequently, the uncertainty center-of-mass coordinates of the current regionV（pi）is the cell（xcentroidal，ycentroidal）,and the center-of-mass equation is

After obtaining the attention point of the attention mechanism,the desired search area of the UAV is obtained using the attention point, and the expression is shown as follows:

wherexAttentionPointandyAttentionPointdenote the position of the current attention point,xvandyvdenote the current position of the UAV, whilexandydenote the coordinates of cell on the line between the attention point and the current position of the UAV,which is illustrated in Fig.9.

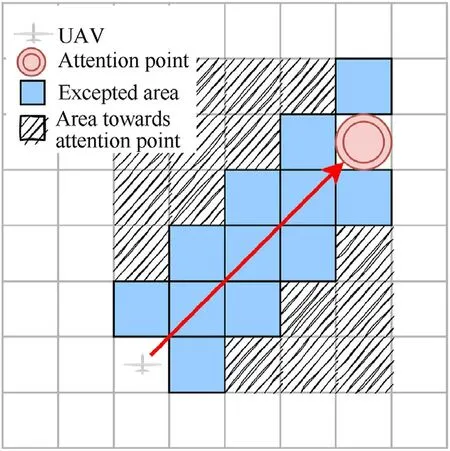
Fig.9.Representation of expected area.

Table 1Initial parameters of target.

Table 2Initial parameters of AACO.

Fig.10.Probability map and uncertainty map processed through attention mechanism.

To improve the cooperative search performance of a UAV cluster under attention mechanism and avoid the waste of resources, a search factordetectjfor path-selection probability is presented.The probabilityPijfor an ant to travel to a path pointjfrom a path pointiis expressed in Eq.(19),where τij（t）denotes the pheromone matrix fromitojat the current time.Here, ηij（t） denotes the heuristic information fromitojat the current time, that is ηij（t） =Jij（t）.α denotes the pheromone heuristic factor, and β denotes the expectation heuristic factor.

wheretjindicates the ratio of undetected cells to all cells within the detection range when the UAV reaches waypointj.

whereAjis the total number of cells that can be detected when the UAV is at waypointj,Djis the total number of detected cells when the UAV is located at waypointj,and ε is its coefficient with a small positive value.When the number of undetected cells increases,the value ofdetectjincreases, and the UAV is more inclined to explore this cell.Thus, the detection efficiency is improved.

The algorithm of AACO is presented in Algorithm 3.

4.Simulation and analysis

Our simulation was conducted in a MATLAB environment.To properly evaluate the proposed approach and analyze its operation in the most realistic way, the AACO algorithm was initially simulated and tested.Subsequently,a simulation test of the cooperative UAV search in communication-restricted scenarios was conducted to verify the effectiveness of the DMPC-AACO.

4.1.Simulation of AACO algorithm

The simulation environment was set as an 30 km×30 km to reflect the search area of a UAV.There were two significant concerns in the area,and the problem parameter settings are listed in Table 1.

The initial target existence probability in the mission area was 0.2, and the mission required the execution of a 200-step search process.According to the scene setting,the parameters of the AACO algorithm were initialized and set.Based on experience,the values of α and β in AACO algorithm are α=3 and β =4,andncycle=150.The specific parameter settings are listed in Table 2.

Fig.11.UAV completes the search of significant concern areas.

First, the target probability map was processed using the environmental uncertainty map according to the attention mechanism, as shown in Fig.10.As the UAV continues to search the region, the environmental uncertainty of the mission area gradually decreases.

Driven by the algorithm,the UAV completed the search for two significant concern areas first, verifying the effectiveness of the attention mechanism.Its trajectory is shown in Fig.11,wherein the UAV completes the search of the significant areas and makes the environmental uncertainty ofNt1, andNt2reduces to 0 at step 31.Subsequently,the UAV completes the search under the guidance of normal concerns.The subsequent search trajectory is shown in Fig.12, and the UAV completes all 200 steps of the search.

The AACO algorithm was compared with the three-algorithm stander ACO algorithm [17], and a random search (RS) strategy based on greedy search algorithm and PSS algorithm [13].Among them, the RS algorithm and PSS algorithms were the search strategies that are applicable in any case.

(1) Stander ACO

The proposed algorithm was compared with the standard ACO to verify the proposed search factordetectj, as shown in Fig.13.It was observed that the stander ACO algorithm featured more overlapping paths around target 1 while performing the search mission and the search efficiency was lower when compared to the AACO algorithm shown in Fig.12.

(2) RS algorithm based on greedy search

The main difference between the RS strategy based on greedy search and the AACO algorithm is that the waypoint at the next moment is selected in a random way without the guidance of heuristic information,and the search efficiency is highly uncertain.The results are shown in Fig.14.It was observed that the UAV did not finish the mission finally.Moreover, compared to the AACO algorithm, the UAV repeatedly searched a large area with the RS.

(3) PSS algorithm

As the PSS strategy is deterministic,the variance of the detection is zero.The results are shown in Fig.15.It was observed that UAV with PSS completed the search for most of the area; however,owing to its deterministic strategy, its search for significant concerns has poor timeliness and cannot cope with unexpected events.If there are large numbers of significant and emergency concerns during the mission, it needs to do a lot of work first, leading to inefficiency.

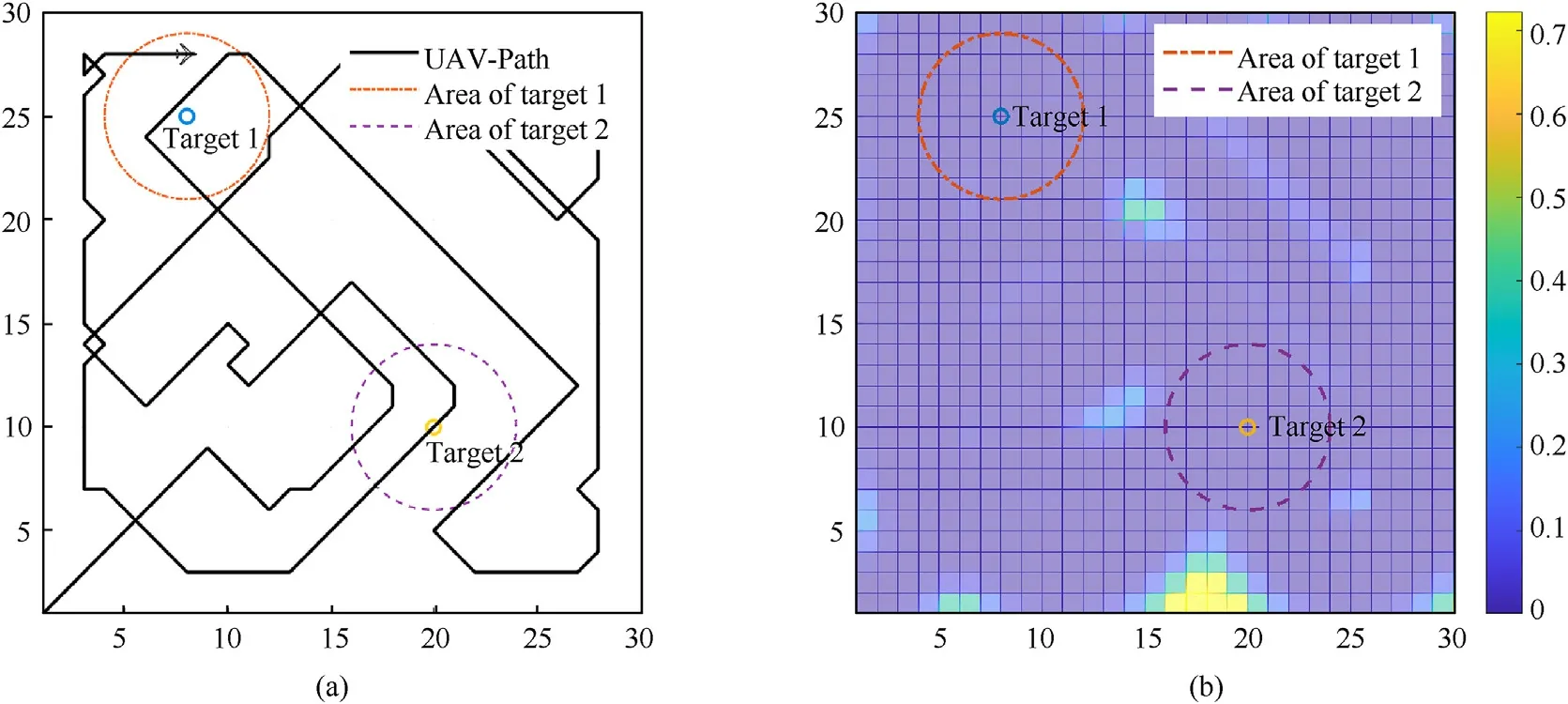
Fig.12.UAV completes 200-step search with AACO.

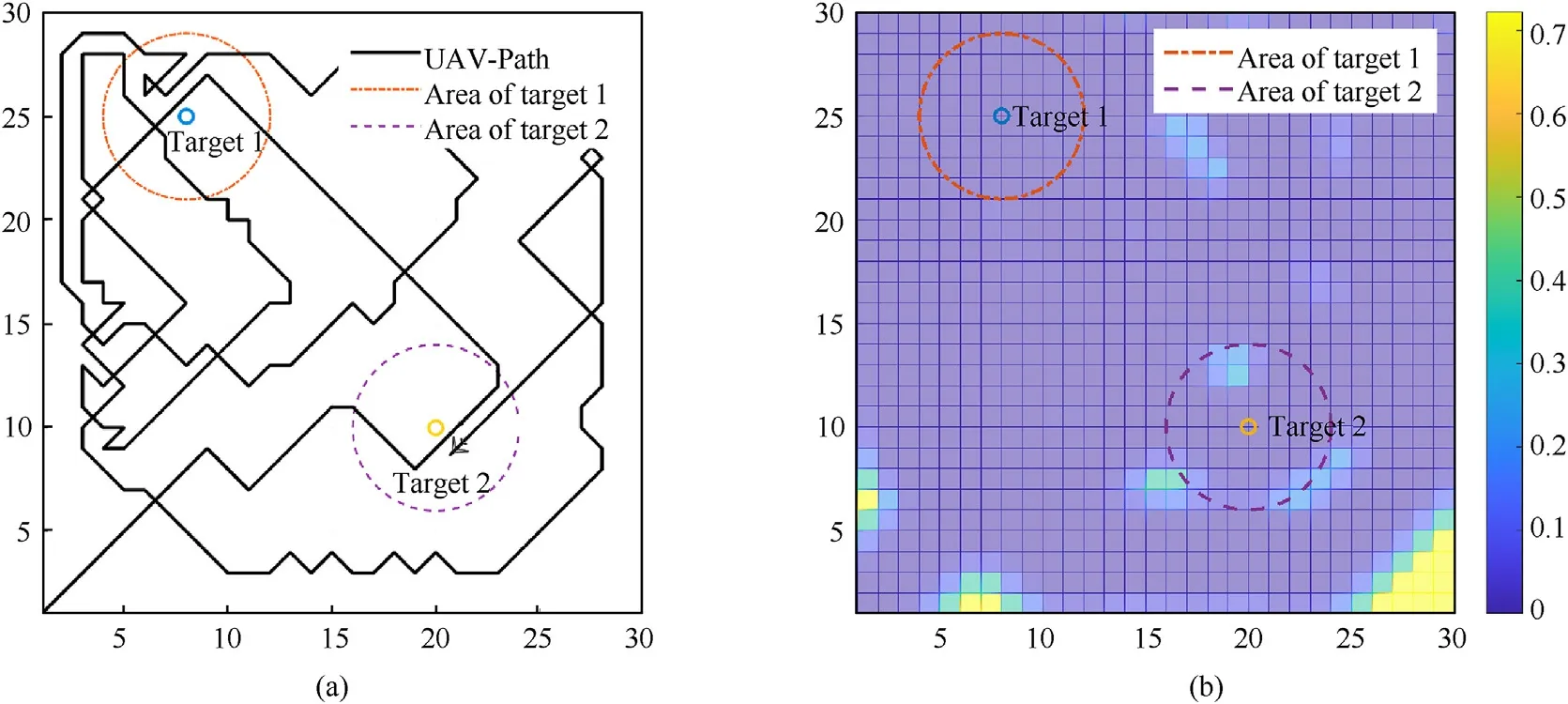
Fig.13.UAV completes 200-step search under with stander ACO.

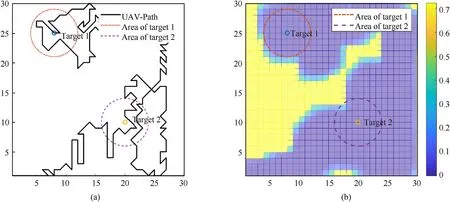
Fig.14.UAV completes 200-step search with RS algorithm based on greedy search.

Fig.15.UAV completes 200-step search with PSS algorithm.

The UAV search processes based on the above mentioned four algorithms were compared, and the average environmental uncertainty during the entire mission scenario was used as the comparison index.The average environmental uncertainty variation curve is shown in Fig.16.It was observed that in the initial stage, the performances of the stander ACO and AACO algorithms were similar, and the search speeds of the PSS and RS algorithms were similar because the map was in an unsearched stage.However,as the search of the mission area progressed,a large number of cells in the area were searched, and the search efficiency of the standard ACO and RS algorithms decreased due to the randomness of the search.Furthermore, the decrease rate of the average environmental uncertainty slowed down.Because the PSS algorithm plans the search route according to parallel lines a prior and searches the unsearched area at every moment,its search efficiency is constant, and the decrease rate of the average environment uncertainty is stable.In this stage, under the traction of attention mechanism, the AACO algorithm proposed in this study satisfied the search for a specific area and ensured stable search efficiency,and the average environmental uncertainty decrease rate remained stable in the early and later stages.Meanwhile, the UAV based on the proposed AACO algorithm achieved the greatest reduction in environmental uncertainty and the greatest benefit in all 200-step searches.

Fig.16.Average environmental uncertainty variation curves of four algorithms.

4.2.Simulation of DMPC-AACO algorithm

For the abovementioned scenarios,the simulation results of four different algorithms are presented.Next, the proposed method to search for multiple targets in a wide area is applied.The scenario was set as follows:

(1) The cluster contained four UAVs in different positions.

(2) The mission area(500 km×500 km)was divided into 500×500 square cells with a unit length of 1 km.

(3) There were 10 special concerns.The target location data,prior probability information of the existence of the target,and region properties are listed in Table 3.

Table 3Initial parameters of targets.

Table 4Initial parameters of DMPC-AACO.

(4) The limitation of no-fly zone was added in this simulation scenario, and the location of no-fly zone is listed in Table 3.

(5) Silent communication required that UAVs communicate with each other every 80 decision steps.

(6) EMI occurred after the communication window at 960 steps;subsequently, the data link failed, and EMI persisted until 1440 steps.

The parameters of the proposed DMPC-AACO algorithm are set as listed in Table 4.The prediction step of the model was 16,execution step was 10, and termination condition of mission was that the environment uncertainty of the entire mission area was less than 0.1.

The results are shown in Fig.17.The circular area in Fig.17(a)represents the area of concern, and the orange rectangular area in Fig.17(a) and the dark rectangular column in Fig.17(b) represent no-fly zones.As shown in Fig.17,the Four UAVs cooperate to reduce the environmental uncertainty to the specified threshold value,and the average uncertainty for the mission area is ＜0.05.

Here, Fig.18(a) shows the positions of UAVs and the division result of search area at the 1000th step, Fig.18(b) shows the division result based on the Voronoi diagram at the 1250th step, and Fig.18(c)shows the division result at the 5000th step.It can be seen from the division results at different times that the proposed division method could accurately divide the respective search areas when the UAVs were in different positions at different times, and the search areas of different UAVs did not overlap.

In the simulation test for the restricted communication scenario,there was a communication window at the 960th step,and the data link between the UAVs was restored to the available state at the 960th step.At this time, the UAVs re-planned the mission area based on the interaction data and the current location information obtained using the algorithm proposed in this study.The replanning results at the 960th step are shown in Fig.19(b).By comparison, it could be observed that the result of the divided mission area had changed,and the UAVs guided by the DMPC-AACO algorithm completed the re-planning of the area when the communication was available.After the 960th step,the situation of restricted communication occurred, and the communication between UAVs could not be completed.At this time, the UAVs searched the divided area under the guidance of the DMPC-AACO algorithm.As all emergency and significant concerns were processed, the point guiding the AACO algorithm was the normal concerns, that is, the center of mass of environmental uncertainty in the current mission area.The search paths of UAVs are shown in Fig.19(c).Wherein, the UAV changed its heading as it approached the divided area line and did not conduct cross-area search,that is,the UAV only focused on the divided search area.

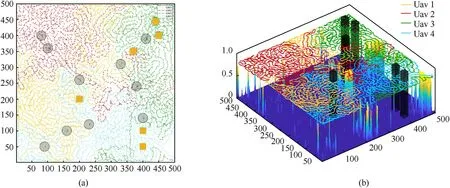
Fig.17.Four UAVs complete the search of 500km × 500 km area with the DMPC-AACO.

Fig.19.(a) Result of area division obtained from the data at the 880th step communication window and executed the search paths.(b) Re-dividing the area at the 960th step communication window.(c) Search path during non-communication period (960th step→1289th step).(d) Results of division obtained from the data at the 1440th step communication window and the search path between the 960th and the 1529th steps.

5.Conclusions

In this study, the main problem discussed was the restricted communication encountered by UAV cooperative search missions in the current complex environment.The key point to solve this problem was to improve the ability of UAVs planning their respective mission areas, avoiding the loss of efficiency caused by repeated search and the loss caused by UAV collisions, and to ensure that UAVs can efficiently complete their respective missions when communication was not available.Based on the mathematical characteristics of Voronoi diagrams, a Voronoi diagram-based partitioning method was proposed to ensure the cooperative search ability of UAVs when communication was unavailable.An attention mechanism ACO based on DMPC framework was also proposed to ensure the efficient search of UAVs during the entire mission.The following conclusions were drawn:

(1) While encountering the problem of cooperative search planning in a complex environment, this study conducted search area division test based on the Voronoi diagram in a limited communication window and effectively solved the problem of search area overlaps and UAV collisions owing to the inability of real-time data interaction among the units in a UAV cluster.

(2) Compared to common algorithms, the DMPC-AACO algorithm proposed in this study reduced the environmental uncertainty to the specified threshold value more rapidly,and exhibited better robustness and reprogramming capability,enabling a better handling of a UAV cluster cooperative search problem in restricted communication scenarios.

(3) By performing simulation tests,the proposed algorithm was verified to achieve the expected goal in communicationrestricted scenarios when communication was both available and not available.Furthermore,it could normally guide the UAVs to complete the search of the mission area in the cases of communication intermittent silence and EMI.

In future, the accuracy of the UAV kinematic equations will be further improved to enhance the degree of simulacra of the algorithm.Simultaneously, the methods of UAV control will be further refined by considering more situations and constraints of missions,and the accuracy and efficiency of system planning will be improved.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors gratefully acknowledge the support of the National Natural Science Foundation of China (Grant No.62076204), the Seed Foundation of Innovation and Creation for Graduate Students in Northwestern Polytechnical University (Grant No.CX2020019),and in part by the China Postdoctoral Science Foundation (Grants No.2021M700337).