Multi-circular formation control with reinforced transient profiles for nonholonomic vehicles: A path-following framework

Jintao Zhang , Xingling Shao ,*, Wendong Zhang , Zongyu Zuo

a School of Instrument and Electronics, North University of China, Taiyuan 030051, China

b State Key Laboratory of Dynamic Measurement Technology, North University of China, Taiyuan 030051, China

c Seventh Research Division, School of Automation Science and Electrical Engineering, Beihang University, Beijing 100191, China

Keywords: Multi-circular formation Reinforced transient profiles Nonholonomic vehicles Path following

ABSTRACT This article investigates a multi-circular path-following formation control with reinforced transient profiles for nonholonomic vehicles connected by a digraph.A multi-circular formation controller endowed with the feature of spatial-temporal decoupling is devised for a group of vehicles guided by a virtual leader evolving along an implicit path, which allows for a circumnavigation on multiple circles with an anticipant angular spacing.In addition, notice that it typically imposes a stringent time constraint on time-sensitive enclosing scenarios, hence an improved prescribed performance control(IPPC) using novel tighter behavior boundaries is presented to enhance transient capabilities with an ensured appointed-time convergence free from any overshoots.The significant merits are that coordinated circumnavigation along different circles can be realized via executing geometric and dynamic assignments independently with modified transient profiles.Furthermore, all variables existing in the entire system are analyzed to be convergent.Simulation and experimental results are provided to validate the utility of suggested solution.

1.Introduction

Over the last two decades, the investigation of multi-vehicle control has aroused increasing interests from industrial and scientific researchers [1-6].As one of the essential parts of coordinated topics, multi-vehicle formation control can substitute humans to accomplish a number of monotonous and dangerous missions such as target capturing [7], environment detection [8]and area monitoring [9].To enable a success of previous missions,existing formation control schemes consisting of cooperative trajectory tracking [6-11] and cooperative path following [12-18]have been presented.As claimed in Ref.[19], the spatial-temporal constraints imposed by a time-based path inherent in trajectory tracking setting always bring about a deteriorated transient performance and a higher probability of actuator saturation.Hence,it is preferred to investigate coordinated path-following control to achieve multi-vehicle collaboration featured with spatial-temporal decoupling.

It is recognized that nonholonomic constraints are typically encountered in plentiful types of vehicles.Thus, extensive cooperative path-following control solutions centered around multiple nonholonomic vehicles have been suggested in Refs.[13-18].In Ref.[13],by utilizing a consensus-based parameterized approach,a distributed controller is constructed for several vehicles to form a parallel formation over multiple open paths.In Ref.[14], an optimized path-following formation problem of robotic vehicles is solved by employing a predictive coordinated control scheme.In Ref.[15], a parallel formation pattern is realized by establishing a cooperative path-guided controller.In Ref.[16],a coordinated pathfollowing control is structured for a fleet of vehicles to form a queue formation along a parametrized path.It should be noted that aforesaid researches concentrate on parallel formation along multiple paths[13-15]or queue formation over an open curve[16-18].However, in occasions where vehicles are deployed to observe,circumnavigate, detect, or capture a target, a circular formation along the same circle is extremely pursued.In Ref.[20], a circular multi-robot formation around a pregiven stationary target is maintained with evenly distributed angular spacing.In Ref.[21], a coordinated path-following controller is proposed by integrating the line-of-sight guidance with a path parameter updating law for multiple vehicles to obtain an equiangular separation between adjacent vehicles over a closed curve.However, for certain enclosing scenarios, vehicles are frequently deployed along different circles to accomplish various tasks,for example,the inside node is specified to monitor the target continuously while the outside one is applied to guard the former against possible attacks.

Notice that although the established parametrized path-guided studies[13-18]can perform a coordination among agents,the path invariance cannot be assured as highlighted in Ref.[22], that is,vehicles may leave away from the pre-assigned path, even if it is already on the reference initially.To surmount this constraint, a pioneering multi-vehicle control is proposed in Ref.[23]to make a consensus via local interactions,achieving a queue formation over an open curve by converting the path-following issue to a nested set stabilization.Nevertheless, aforementioned outcomes [13-23]can only compel the error convergence towards the origin with a finite time or an exponential stability,and the regulation of settling time is heavily related to initial errors and control arguments.Particularly,when initial positions of vehicles are far away from the reference path, a remarkable initial path-following error inevitability results in a fairly long convergence phase, giving rise to a disappointed transient performance that apparently transgresses the time limits of cooperative missions.

How to impose predesigned constraints on cooperative behaviors free from repeatedly regulating controller arguments is an ongoing and active research issue in the past few years.To address such problem, an efficient prescribed performance control (PPC)alternative is well explored in Refs.[24-29] for various multivehicle formation scenarios.In Ref.[25], by integrating a PPC with the traditional robust controller,a singularity-free continuous control behavior of multiple underactuated vehicles can be obtained.In Ref.[26], a distributed synergetic learning control strategy with a prescribed performance is proposed for multi-vehicle system to improve the formation performance.In Ref.[27], based on the PPC approach, a leader-follower attitude control is interviewed to attain spacecraft formation errors within the prespecified range.However, it should be emphasized that reported PPC-based cooperative controllers investigated in Refs.[24-29]can only guarantee an asymptotic convergence on account of utilizing an exponential-type performance envelop, that is, the constrained states would reach the steady-state values in an infinite time, which is unacceptable for most of coordinated tasks with a strict time restriction.To overcome this shortage [30], presents an appointed-time attitude tracking controller for spacecraft in light of a continuous and piecewise function.Similarly, a fault-tolerant control approach is proposed in Ref.[31] to enforce quadrotor attitude controlling error approximate to prespecified ranges before an appointed time.In Ref.[32],a multi-agent formation with an improved transient performance is provided by utilizing a leader-follower appointed-time control strategy.Although the overshoot of system states can be confined within a preassigned range by enforcing the existing schemes [30-33], it still cannot guarantee a sufficiently small overshoot, such that a higher probability of actuator saturation may be occurred during transient stage.Therefore, how to modify the reported PPC scheme to allow for multi-circular path-following formation with reinforced transient behaviors free from overshoots is still an open and challenging topic that should be urgently investigated.

Enlightened by the aforesaid statements, a multi-circular formation control with reinforced transient profiles is proposed for networked nonholonomic vehicles under path-following framework.The primary innovations are highlighted as follows.

■Compared to the prevalent trajectory tracking control studies[6-9], where spatial-temporal constraints are highly imposed,herein the geometric and dynamic missions can be regulated separately, resulting in a smooth transient performance and a lower probability of actuator saturation.In addition, distinguishing from existing path-guided cooperative control results focusing on parallel pattern along multiple paths [13-15] or queue pattern over an open curve[16-18], herein a cluster of vehicles are designated on different circles to generate a multi-circular formation with an expected phase distribution.Contrasting to the circular enclosing paradigm [21] that achieves coordination over a common orbit via synchronizing path parameters,herein by formulating coordinated errors in terms of separation angles,a multi-circular circumnavigation can be implemented by constructing a velocity regulation rule to stabilize cooperative deviations,which is more straightforward and concise in controller expression.

■In contrast to the reported coordinated path-following outcomes [13-23], where the regulation of settling time is highly subjected to initial errors and controller parameters,herein without resorting to tedious parameter selection, an improved prescribed performance control(IPPC)is proposed by specifying the error convergence profile as a prior.Furthermore, distinguishing from the previous PPC-based controllers [24-29] only enforcing system states to reach the pre-devised range with an exponential rate, the suggested IPPC is able to provide a given-time transient convergence with the aid of defining novel behavior boundaries related to Han’s tracking differentiator (Han’s TD).Besides, unlike the reported appointed-time schemes[30-33], the suggested IPPC can guarantee the overshoot of involved error to be sufficiently small by introducing tighter transient envelopes.Moreover, an experimental validation with multi-circular formation control using IPPC is conducted for the first time.

The remainder of this paper is arranged as follows.Problem description is provided in Section 2.Section 3 gives the main results.Simulation and experimental results are depicted in Section 4.Conclusion is stated in Section 5.

2.Problem description

Consider a networked nonholonomic vehicles system depicted in Fig.1,which consists ofNfollower vehicles,labeled as vehicle 1 toNand a virtual leader, labeled as vehicle 0.

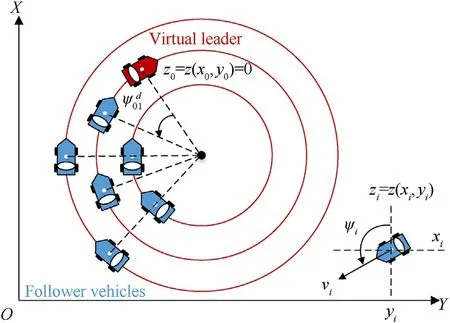
Fig.1.Diagram of multi-vehicle systems.

Referring to Ref.[20], the kinematics ofith vehicle can be described by

wherexi，yiand ψirespectively denote the position and heading angle ofith vehicle in inertial frame.viand ωirespectively represent the linear and angular speeds with vi＞0.Let the virtual leader evolve along an implicit circular path,formulated by z = ｛［x，y］T∈=ax2+by2-r2=0｝,wherez（x，y）is a continuous and differentiable function,a，bandrare arguments to be designed.Obviously, the virtual leader fulfillsz0=z（x0，y0） = 0.

3.Main results

3.1.Multi-circular formation controller design

In this subsection,under a path-following architecture,a multicircular formation controller consisting of two parts is devised for multiple nonholonomic vehicles to realize the geometric and dynamic tasks, wherein the geometric assignment is to drive all vehicles to follow the implicit reference path by pursuing an angular speed control law,and the dynamic assignment aims to construct a forward speed control law to stabilize coordinated error in light of separation angles, such that multiple vehicles can be steered to form and preserve a multi-circular formation over different circles.

3.1.1.Angularspeedcontrollawdesign

Letzi=z（xi，yi）+pirepresent the position error ofith vehicle,wherepiis a constant deviation with regarding to the virtual leader on the implicit circle.Then, define the first-order partial differentials ofziaszix，ziy, respectively.zixx，zixyandziyycorrespondingly denote the second-order partial differentials.Subsequently, according to Ref.[23],the desired heading angle and angular speed ofith vehicle are respectively devised as

In the sequel, by synthesizing the position and heading angle tracking deviations,a path-following error variableeisis introduced to steer each agent towards the reference circles.

whereki1is a positive constant.

To realize the geometric assignment, an angular speed control law is constructed to eliminate the path-following erroreisas follows:

whereki2is a positive constant.

3.1.2.Forwardspeedcontrollawdesign

Subsequently, to achieve the cooperative actions of multiple vehicles and ultimately form a circular formation on multiple circles guided by a virtual leader, a coordination erroreiψ is established as follows:

Remark 1.It should be mentioned that the spatial position relation of adjacent vehicles can be conveniently deduced from the sign of,particularly,for clockwise rotation,＜0 represents that vehicleiis in front of vehiclej,and vice versa,greatly promoting the implementation of achieving coordination along multiple reference circles.In addition, the interaction behaviors among vehicles are described by a digraph G rather than an undirected graph utilized in Ref.[34],which is more general in practices.Moreover,since the computation of coordination error only entails the information of adjacent agents, triggering a distributed control setting, i.e., the overall calculation cost will not increase remarkably as the number of nodes aggravates.

To stabilize Eq.(7), a novel forward speed control law is established to perform on-path formation behaviors.

where 0 ＜κi≤1 is a design parameter employed to directly regulate the velocity boundary of each vehicle.v0is a preassigned velocity constant of virtual leader.ki3is a positive argument.

Remark 2.The forward speed control law Eq.(8)proposed in this article is designed to achieve the dynamic task,which is totally different with the reported trajectory tracking control [35-39], as can be clarified from following aspects.One is that in our design,the velocity control and angular rate control laws are separately devised to yield a spatial-temporal path following setting,which is more convenient for implementation.Oppositely, for the existing trajectory tracking paradigms[35-39],one typically calculates the velocity vector command containing information of velocity magnitude and heading angles,thus design of velocity and angular rate rules are highly coupled, severely depending on the imposed time-related references.Another is that physical velocity constraints can be naturally maintained for suggested velocity controller,as demonstrated from Eq.(8),it is intuitive that velocity command is rigidly limited within （v0（1 - κi）‖∇zi‖/‖∇z0‖，v0（1 +κi）‖∇zi‖/‖∇z0‖）, while for the reported trajectory tracking algorithms, the input constraints on velocities are not considered.To sum up, the involved path following controller can address geometric and dynamics missions individually and adapt for regulation of unmanned systems experiencing strict velocity limitations.

Remark 3.Notice that the computation of Eq.(8)relies on the global information of leader velocity v0, breaking the essence of distributed control.But it is not a new and challenging issue to eliminate the demand of preassigned leader velocity v0being accessible to all vehicles, one can use the mature distributed observers [21,40-42] to reconstruct the leader velocity via local interaction, delivering a fully distributed control setting.

Lemma 1.[23].Consider a digraph G related to a spanning tree with the virtual leader being root node, there always exist nonnegative real components for all the eigenvalues of matrix L +B.

Theorem 1.Given a networked multi-vehicle system including follower vehicles and one virtual leader designated over the preplanned circle,and the communication relationship among vehicles conforms to Lemma 1.Then, the geometric and dynamic assignments can be solved by the proposed multi-circular formation controller consisting of an angular speed control law Eq.(6)and a forward speed control law Eq.(8).

Proof.To demonstrate the asymptotic convergence ofeisandeiψ,the following two steps are provided.

Step 1.Recalling Eq.(5), the time derivative ofeiscan be expressed as

Next, substituting Eq.(6) into Eq.(9), one can infer

Obviously,eisfulfills asymptotic convergence condition, that is,ast→∞, we can obtain that ψie→- arctan（ki1zi）.Then, whent→∞, error dynamics of position can be formulated as

Constructing the candidate Lyapunov function asSince ‖∇zi‖vi＞0 holds, it can be deduced that

Therefore, one can derive that bothziand ψiecan satisfy asymptotic convergence, i.e., each vehicle can be asymptotically driven to the reference circle by resorting to the established angular speed control law Eq.(6).

Step 2.Note thatzixy=0andzixx=ziyy=2 can be readily calculated for a general circle.By substituting the values ofzixy，zixxandziyyinto Eq.(3), it can be inferred that

Then, taking the time derivative ofeiψ, one has

Next, define two matrices Eψ∈RN×1and ψ∈RN×1as

One has

Substituting Eq.(8) into Eq.(16), it can be put into

where αi≜［1 + κitanh（ki3eiψ）］（cos ψie- 1）, which is obviously bounded.Therefore, by treating αias the input, system Eq.(17)holds input-to-state stability.Next, since ψieconforms to asymptotic convergence property according to Step 1,it is obvious that αifulfills asymptotic convergence.Thus, the asymptotic convergence of coordination erroreiψcan be directly arrived in light of Lemma 1.Then, it can be concluded that all error dynamics of entire closedloop system are analyzed to be limited.Additionally, revisiting Eq.(8), the moving velocity of follower vehicles will approximate to v0‖∇zi‖/‖∇z0‖ ultimately.Hence the proposed multi-circular formation controller is qualified in driving a cluster of vehicles to achieve a circumnavigation over multiple circles,that is,geometric and dynamic tasks can be well accomplished.

3.2.Multi-circular formation controller with IPPC

In the previous section, a multi-circular formation control strategy featured with an asymptotic convergence is designed,implying that each vehicle can ultimately reach the predesigned circle ast→∞,which cannot be tolerated for coordinated practices exposed to rigorous time constraints.To surmount this drawback,a modified multi-circular formation controller endowed with reinforcing the transient behaviors is investigated by exploring the proposed IPPC, such that path-following error of each vehicle can be forced to converge within a user-prescribed bound before a given time free from overshoots.Relevant architecture of modified strategy is depicted in Fig.2.

Definition 1.The functionh（t）:｛R+，0｝→R+is known as an appointed-time performance function on condition thath（t）holds the following properties: (1)h（t） is a nonnegative and monotonic decreasing function overt∈［0，ta）.(2)h（t）=h∞for ∀t≥ta,wheretais a user-assigned reaching time, andh∞is a nonnegative constant.

To ensure the convergence of path-following erroreiswith arbitrarily small overshoot, by defining novel lower and upper boundary envelopes, an IPPC featured with an appointed-time decaying without overshoots is devised to ensure the fulfillment of the following inequality, as depicted in Fig.3.

wherehi0，respectively represent the initial values ofhiand ϖi.hi∞denotes a tunable nonnegative scalar employed to regulate the ultimate size.δ is the sampling interval.σidenotes the acceleration factor used to adjust the decreasing rate ofhi.Note that the selection ofhi∞should satisfy |hi∞|＜|hi0| on account of that the performance functionhiis monotonically decreasing.Besides, as claimed in Ref.[43], the settling time ofhican be calculated asclearly it is given-time convergent obeyingDefinition 1and oncehi0andhi∞are selected, different settling times can be straightforwardly prescribed by choosing various acceleration factors, particularly, a minor σiwill yield a slower convergence phase, as described in Fig.4.

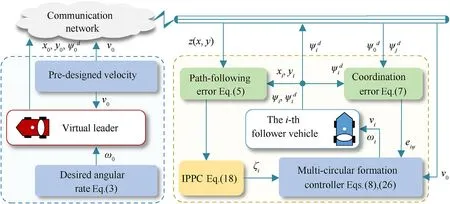
Fig.2.Architecture of multi-circular formation controller.

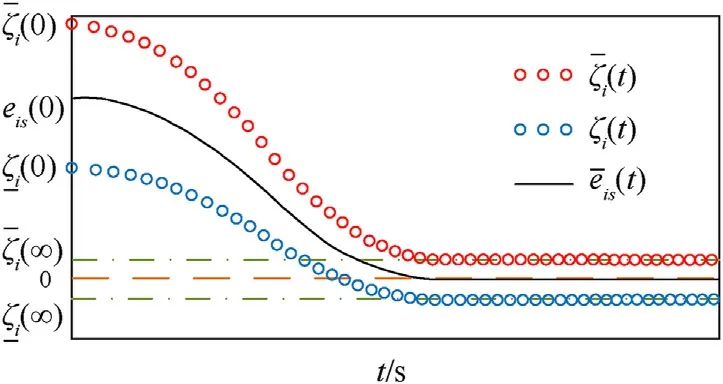
Fig.3.Graphical illustration of suggested IPPC.

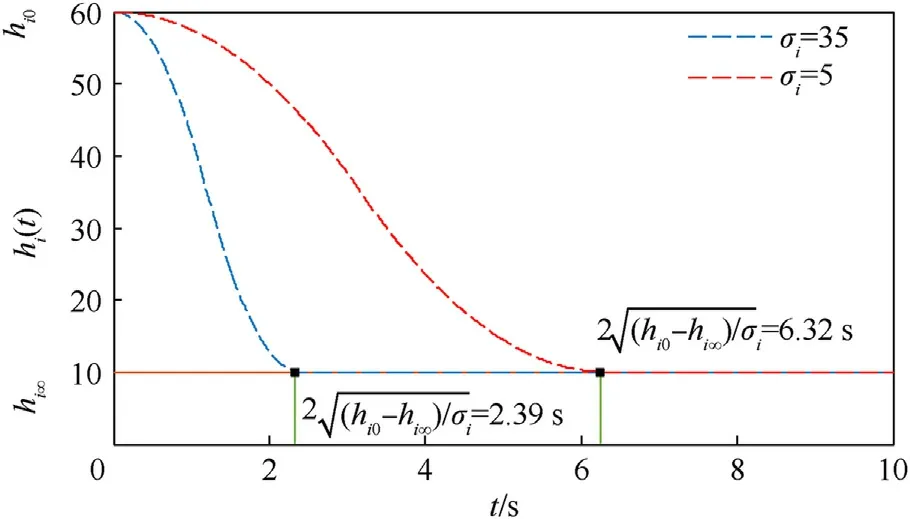
Fig.4.Appointed-time convergence performances of IPPC.

Remark 4.The prominent characteristics of proposed IPPC can be outlined from the following aspects: In contrast with the accessible cooperative path-following schemes[13-23],where the settling time is heavily associated with initial conditions and control arguments,herein the proposed IPPC is able to specify the error convergence profile as a prior free from repeated parameter regulation.Additionally, distinguishing from the previous PPC-based controllers [24-29] only enforcing system states to converge within the pre-devised range with an exponential rate, herein the suggested IPPC can provide a given-time transient convergence with the aid of defining novel behavior boundaries related to Han’s TD as described by Eq.(21).Moreover, different from the reported appointed-time schemes [30-33] that cannot hold transient overshoots within an adequately small size, as illuminated in Fig.5,owing to the opposite signs of initial values in behavior functions,great overshoots are typically enforced, to circumvent such drawback, herein the starting signs of upper and lower boundaries are selected the same with the sign of initial error, thus we make additional efforts in redesigning the imposed constraint boundaries, allowing that the proposed IPPC can guarantee the error overshoot to be sufficiently small by devising tighter transient envelopes, shown in Fig.3.

Subsequently, to promote the controller development holding performance constraints given by Eq.(18), an error conversion function is designed as below.

with

where ςi（t） denotes the transformed one of path-following error.Then, taking time derivative of ςi（t） has

with

Fig.5.Graphical illustration of existing PPC.

Next, to eliminate the converted path-following error, a modified angular speed control law is constructed as follows:

Theorem 2.Given the entire closed-loop system including nonholonomic vehicle dynamics Eq.(1),the forward speed control law Eq.(8) and modified angular speed control law Eq.(26), the coordination erroreiψ will converge to origin asymptotically and the transformed path-following error ςipreserves to be convergent before a user-defined time without overshoots, andcan be obtained,i.e.,all vehicles are able to reach reference circles with reinforced transient profiles and ultimately form a multi-circular formation around a stationary target.

Proof.Substituting Eqs.(9) and (26) into Eq.(24), one can acquire

It can be easily deduced that ςiis convergent,hence there has a nonnegative constant ςiMholding |ςi（t）|≤ςiM.Next, to reveal the convergence ofeis（t）, rewrite Eq.(22) as follows:

Then,χi（t） becomes

In the sequel, resorting to|ςi（t）|≤ςiM, which can be converted as-ςiM≤ςi（t）≤ςiM.Next,for the monotonously increasing function χi（t）, one can infer

Recalling Eq.(23), it has

On the basis of Eq.(31), we can obtain

Note that the proof process ofeiψis similar to subsection A,the related procedure is omitted here.Consequently, the proof is completed.

Fig.6.Communication topology among vehicles.

Table 1Controller parameters of proposed strategy.

Fig.7.Simulation results: (a) Formation pattern along multi-circles constituted by six nonholonomic vehicles; (b) Forward speeds of six vehicles and virtual leader; (c) Angular speeds of six vehicles; (d) and (e) Path-following errors of six vehicles using IPPC; (f) Coordination errors of six vehicles.

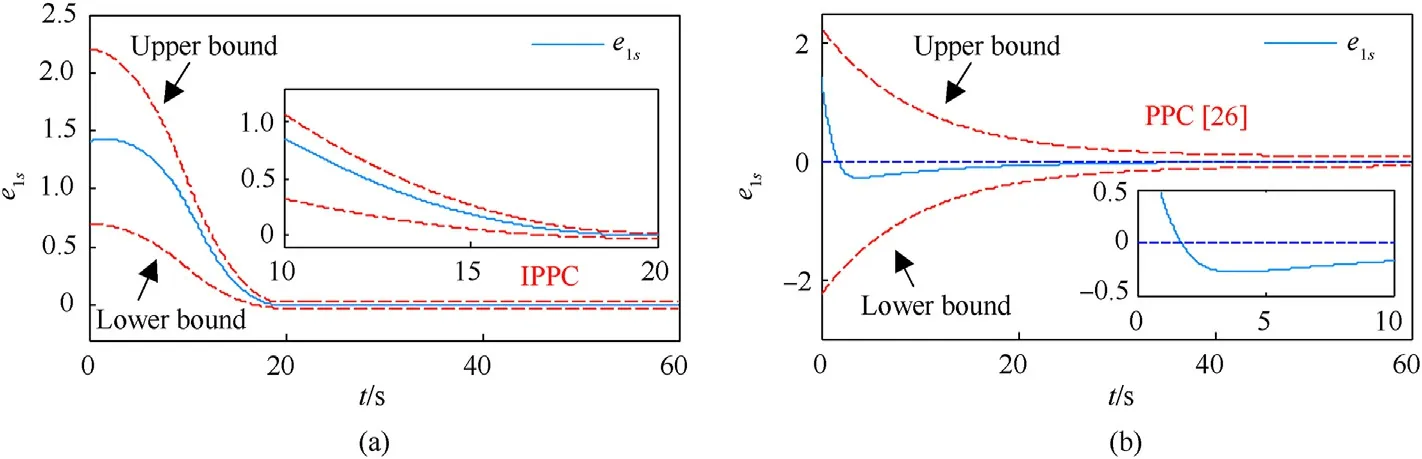
Fig.8.Comparison between proposed IPPC and PPC [26].

Remark 5.To promote the online implementation of proposed scheme, fundamental adjustment policies relative to controller arguments are concluded as follows: (1) For controller module, a faster error stabilization can be acquired by large control gainski1，ki2andki3.However, overlargeki1，ki2andki3may trigger unwelcome transient chattering.Hence, a tradeoff is recommended to make between convergence rate and stability.Additionally, the changing interval of forward speed is concerned with the value of κi, and an appropriate selection is preferred such that hardware constraints are not transgressed.(2) For IPPC, the selection ofshould guarantee the fulfillment ofand the final boundaryis determined with consideration of the resolution of amounted sensors.Furthermore,the acceleration factor σishould be adjusted properly to allow for a bounded convergence time driven by limited capacities of vehicle actuator in practices.

4.Simulation and experimental results

4.1.Simulation results

Two simulations are carried out to demonstrate the efficiency and advantage of presented control scheme in this subsection.Related simulations are constructed under Matlab/Simulink software with a sampling frequency being 100 Hz.

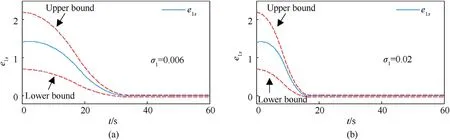
Fig.9.Comparison of path-following errors of IPPC under different envelopes.

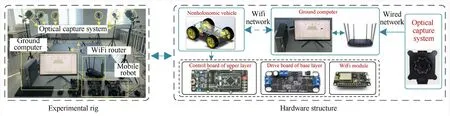
Fig.10.Physical test bench and interconnections between modules.

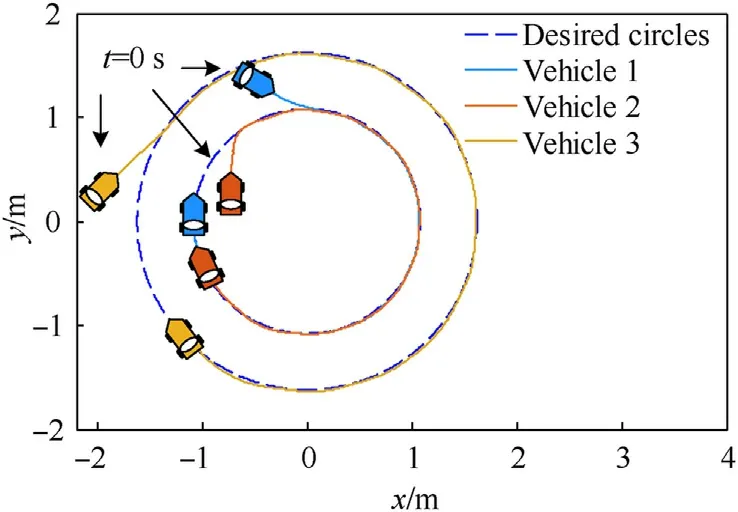
Fig.11.Multi-circular formation pattern formed by three vehicles.

Fig.12.Forward speeds of three vehicles.

Fig.13.Angular speeds of three vehicles.

The networked multi-vehicle system is composed by six nonholonomic vehicles and one virtual leader operating along a predevised circlez（x，y）=x2+y2-502=0 at a constant forward speed v0= 1 m/s.The communication topology among vehicles is described by Fig.6, and one can obtain that diagonal matrix B =diag｛1，0，0，0，0，0｝ anda12=a23=a34=a45=a56= 1, by treating the virtual leader as the root node,it can be easily examined that the involved topology holds Lemma 1.Additionally, the initial positions and orientation of each agent are set asx0= 0，y0= 50，ψ0= 0，x1= - 20，y1= 54，ψ1= 0.32，x2= - 40，y2= 60，ψ2=0.54，x3= -15，y3=26，ψ3=0.55，x4= -37，y4=20，ψ4=0.90，x5= -65，y5=30，ψ5=1.21，x6= -28，y6=10，ψ6=1.13.The regulation parameters of the proposed controller are listed in Table 1,following argument regulation rules outlined in Remark 5.

4.1.1.Simulation1:efficiencyvalidation

Simulation results are depicted in Fig.7.Multi-circular formation behaviors composed by six vehicles are provided in Fig.7(a),showing that six vehicles with different initial states are able to converge to desired circles and form a multi-circular pattern with pre-devised phase angle spacing at constant forward speed under the presented strategy.And the case without using IPPC is exhibited in subgraph of Fig.7(a), demonstrating that IPPC can effectively improve the convergence process.The forward and angular speeds of six vehicles are respectively shown in Figs.7(b) and 7(c).The path-following error is depicted in Figs.7(d) and 7(e), exhibiting that all path-following errors can converge within the preselected range before an appointed time without overshoots under proposed IPPC, i.e., geometric task is well accomplished with reinforced transient profiles.The coordination errors are plotted in Fig.7(f), indicating that the multiple vehicles can finally form and guarantee the circumnavigation on multiple circles with prespecified phase angle spacing, that is, dynamic objective is well achieved under local information exchange.

Fig.14.Path-following errors of three vehicles using IPPC.

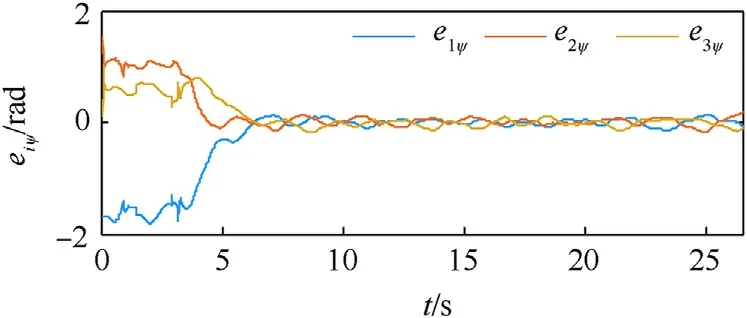
Fig.15.Coordination errors of three vehicles.

4.1.2.Simulation2:comparisonwithPPC[26]

To confirm the advantages of presented IPPC in terms of arbitrarily small overshoot and appointed-time convergence, comparisons with traditional PPC [26] are provided.Notice that relevant controller parameters are dedicatedly adjusted to ensure almost the same prescribed times.Comparison result is depicted in Fig.8,it can be observed that both approaches can impose the system state within the predefined range.However, under traditional PPC technique, the convergent profile is inevitably subject to obvious overshoots during the initial period.On the contrary,by observing Figs.8 and 9, it can be concluded that the proposed IPPC can achieve a satisfactory appointed-time convergence with an arbitrarily small overshoot in spite of different behavioral envelopes.

4.2.Experimental results

In this subsection,to further verify the effectiveness of proposed scheme, a multi-circular formation experiment is performed on a physical test bench.As exhibited in Fig.10,the entire multi-vehicle platform is composed by three vehicles marked with fluorescent dots, a ground computer and an optical capture system.Each vehicle is equipped with a microcontroller chip LPC54606J512 as control board of upper layer to perform the presented strategy with a fixed sampling period being 0.02 s,a drive board of base layer to precisely follow commanded forward speed and angular speed signals, and a 2.4 GHz Wi-Fi module to acquire the network information.The cooperating systems operate on the following principle: Firstly, through identifying fluorescent dots equipped on each vehicle, the optical capture system with a positioning resolution being ±1 cm is employed to measure positions and orientation of vehicles and transmit the measurement data to ground computer via a wired network.The ground computer is utilized to plan the desired circles and broadcast to vehicles via a wireless network.With the received messages and onboard measurement data related to forward speed and angular speed, a group of vehicles start to implement the proposed control scheme by control board of upper layer.Additionally, owing to the absence of global positioning system signals under an indoor scenario,herein an external position determination solution is used, thus information flow is transferred between ground computer and each agent rather than inter-vehicle exchange, this point is different from the previous simulations.However, since we use the communication topology 0→1→2→3→1 to enable the adjacent weights, i.e., only a fractional of neighboring information instead of all nodes is participated to yield the cooperative path-following control item,therefore the computational complexity of suggested scheme will not remarkably increase with the increase in agent numbers.

In the experiments,the desired circle is selected asz（x，y）=x2+y2-1.12=0 due to limited space, the forward speed of virtual leader is chosen as v0=0.22 m/s,the related controller arguments are set aski1= 0.02，ki2= 0.16，ki3= 8.5，κi= 1，pi= 0，c10= 0，c12=c23= -0.3，c31=0.6，δ =0.01，，h10=0.8，h20=h30= 0.5，hi∞= 0.1，σi= 0.08，（i= 1，…，3）.And the experimental results are provided in Figs.11-15.The multi-circular formation pattern composed of three vehicles is depicted in Fig.11, which certifies that several vehicles can well realize both geometric and dynamic objectives.Figs.12 and 13 respectively reflect the measured forward and angular speeds of three vehicles.Furthermore, the path-following errors are plotted in Fig.14 without violating the prescribed performance limitations and coordination errors of three vehicles are drawn in Fig.15,shown to be convergent and bounded.To sum up, the existing results further demonstrate the utility of control scheme for multi-vehicles.

5.Conclusions

In this paper, a multi-circular path-following formation control with reinforced transient profiles is investigated for nonholonomic vehicles connected by a digraph.By employing the proposed multicircular formation controller, multiple vehicles can form and guarantee a circumnavigation around a target on multiple circles with preassigned anticipant angular spacing.In addition, an IPPC strategy is studied to further improve multi-agent transient behaviors,i.e.,each agent can be steered to the reference circle before an appointed-time with arbitrarily small overshoots.The stability of entire system is proven in light of input-to-state stability.Simulation and experimental results verify the utility and superiority of presented control scheme.

Further direction will cover developing an adaptive dynamic programming control scheme for multiple vehicles to avoid the collision among agents and acquire the optimal cooperative control performance.And it is also more appealing to integrate with lowfrequency quantized control method [44] to reduce the network burden.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant Nos.62173312 and 61803348, in part by the National Major Scientific Instruments Development Project under Grant No.61927807, in part by the Program for the Innovative Talents of Higher Education Institutions of Shanxi and Shanxi Province Science Foundation for Excellent Youths,in part by the Shanxi "1331 Project" Key Subjects Construction (1331KSC), in part by Graduate Innovation Project of Shanxi Province under Grant No.2021Y617.