Experimental and numerical investigation on alternatives to sandy gravel

V.Denefeld , H.Aurich

a Fraunhofer Institute for High-Speed Dynamics, Ernst-Mach-Institut (EMI), Ernst-Zermelo-Str.4, 79104, Freiburg, Germany

b Fraunhofer Institute for High-Speed Dynamics, Ernst-Mach-Institut (EMI), Am Christianswuhr 2, 79400, Kandern, Germany

Keywords: Improvised explosive device (IED)Specific impulse Momentum transfer Sandy gravel Glass spheres Numerical model Soil moisture

ABSTRACT The NATO agreement STANAG 4569 defines the protection levels for the occupants of logistic and light armored vehicle.The Allied Engineering Publication, AEP-55, Volume 2 document outlines the test conditions for underbelly improvised explosive device (IEDs), which must be buried in water-saturated sandy gravel.The use of sandy gravel has some drawbacks, for instance reproducibility, time consumption, and cost.This paper focuses on the investigation of four alternatives to sandy gravel, which could produce similar specific and cumulative impulses: a concrete pot filled with water, a concrete pot filled with quartz sand, a steel pot without filling and a concrete pot filled with glass spheres (diameter 200 μm-300 μm)and different water contents.The impulses are measured with a ring technology developed at the Fraunhofer EMI.A numerical soil model based on the work of Marrs, 2014 and Fiˇserov'a, 2006 and considering the soil moisture was used to simulate the experiments with glass spheres at different water contents, showing much better agreement with the experiments than the classical Laine & Sandvik model, even for high saturation levels.These results can be used to create new test conditions at original scale that are more cost-effective, more reproducible and simpler to manage in comparison to the current tests carried out with STANAG sandy gravel.

1.Introduction

The protection levels for the occupants of logistic and light armored vehicles are defined in the NATO standardization agreement STANAG 4569 [1].STANAG specifies the agreement of member nations to implement a standard in order to meet an interoperability requirement.The assessment of a specific protection level for military vehicles is carried out using test methods defined in the Allied Engineering Publication AEP-55, Volume 2.This document describes the threat definitions,test conditions and crew injury criteria of vehicle occupants to be used when determining the protection level of armored vehicles subject to classical grenade and blast mine threats.It describes the test condition for underbelly improvised explosive devices (IEDs), which is a surrogate TNT mine buried in water-saturated sandy gravel.A drawback of using sandy gravel for testing vehicles is that it causes a greater variability in blast pressures than other soil types [2,3],despite the specification of the granulometry and the moisture content of sandy gravel.The test procedure with sandy gravel and the filling of a test pit of 2 m×2 m is also very time consuming and cost intensive.Rigby et al.[2] showed that variability in localised loading is intrinsically linked to the particle size distribution of the surrounding soil.Therefore,there is a significant interest to explore alternatives to sandy gravel.

This paper focuses on the investigation of alternatives to sandy gravel, which could produce similar specific and cumulative impulses on a structure above the detonating charge.When fulfilling these two conditions, the alternatives are expected to generate similar deformations of the vehicle floor as a HE (high explosive)charge embedded in sandy gravel,assuming that the floor behaves impulsively.Special attention has been given to a detailed description of the sand or gravel embedding material.A numerical model considering soil moisture is needed to simulate soil with different water contents[4-6].Scientific work concentrated on the analysis of the charge embedding geomaterial preparation and the correlation of burial conditions with the momentum transfer[7-10].In many test devices, only the global momentum transfer on a large-area structure was examined.For a better understanding of the loading process, locally resolved information about the specific impulse distribution on a structure is necessary[11-13].A new test technology based on a ring arrangement was developed at the Fraunhofer EMI and presented in Ref.[14].The principle idea is to measure the velocity and thus the momentum transfer of different rigid bodies at different spatial positions that are exposed to the detonation of the buried HE charge.The exposed surface areas of the objects determine the local resolution of the specific impulse measurement.Our test technology is based on an arrangement with concentric rings where each individual ring is used as a momentum trap at the corresponding local position.The ring system located above the detonating charge is accelerated and each ring velocity is experimentally determined.The ring technology has been proven reliable to measure the influence of burial conditions on the impulse transferred onto the vehicle[15,16].Held[12] used steel momentum gauges placed at different angles to measure the variation of the impulse with very high polar angle resolution,but he did not measure the impulse as a function of the lateral distance to the charge.Ehrgott et al.[17] designed an impulse measurement device to capture the total impulse which cannot measure the specific impulse.Fourney et al.[18] used targets of different sizes to measure the total impulse and small plugs inside a steel plate to measure the specific impulse,but the number of plugs and therefore the measurement of the specific impulse is limited to five laterally.Regarding the ring technology developed at the EMI [14], X-ray imaging and high-speed video were used to measure ring velocities.The different diagnostic tools used gave very consistent results.It was shown that the use of an analytical formula to quantify the specific impulse distribution overestimates the experiments by about 50%and thus can only be used for a rough estimation of buried charge detonation effects.Rigby et al.[2]used also a quarter scale experimental setup with Hopkinson pressure bar arrays to determine the specific impulse,but the instrumented region is limited to 100 mm laterally.

Four different set-ups were tested as possible alternatives to sandy gravel: firstly, a concrete pot filled with water, secondly, a concrete pot filled with quartz sand of different water contents(0%,15%,25%),then a steel pot without filling and finally a concrete pot filled with glass spheres (diameter 200 μm-300 μm) of different water contents(0%,17%,23%).The use of a concrete pot instead of a large test pit reduces material consumption.Water, quartz sand,and glass spheres were selected for their uniformity to ensure more reproducible results, unlike the varying grain size and saturation level found in sandy gravel.The steel pot, mentioned as a possible alternative in AEP-55, Volume 2, was also included in the testing.

2.Measurement of the specific and total impulse

The experimental setup for the determination of the local specific impulse and the total impulse is shown in Fig.1.The sizes for the setup have been driven by the surrogate TNT mine presented in the AEP-55,Volume 2 and scaled down by a factor of 4.3 in order to be tested in the test facility.The first setup,shown on the left side,is used to determine the local specific impulse and consists of eight concentric rings with a thickness of 20 mm and with heights ranging from 60 mm to 140 mm and an additional outer steel plate with a diameter of 1200 mm and a thickness of 10 mm.The dimensions are chosen to ensure best separability of the different rings in the flash radiographs and to prevent the rings from degrading the ceiling.The size of the outer steel plate was chosen to capture as much impulse as possible.Special attention has been devoted to the choice of an appropriate gap size between the rings of 0.2 mm,small enough to prevent that sand fills the gap,and large enough to minimize friction.On top of that, silicone gel has been added between the rings and it has been checked before each experiment that the rings could slide up freely.After detonation of the charge, the rings are accelerated and reach a constant velocity after 2 ms-3 ms, named initial velocity.The specific impulse is calculated by multiplying the initial velocity of each ring by the mass of the ring, divided by the base area of each ring [14].The impulse of a ring is obtained by multiplying its specific impulse by its base area.The cumulative impulse is calculated by adding the impulses of the rings.Finally, the total impulse is obtained by adding the impulses of all rings and plates.A redundant velocity measurement of the rings was realised, using both flash X-ray technique and Photonic-Doppler-Velocimetry (PDV) [19].A comparison of the two methods was made for ring#3,for tests 8 to 13,showing that the difference between the two velocity measurements was less than 7%, thus ensuring their validity.The second experimental setup consists of one single steel plate with a diameter of 1200 mm,the same diameter as the outer steel plate of the first setup, to determine the total impulse.A thickness of 16 mm was chosen to prevent the plate from being deformed and to make the plate easy to handle.After detonation, the plate is being accelerated and the motion is superimposed by vibrations.To determine the initial velocity of the single plate and the outer steel plate, the velocity deduced from the PDV signal is averaged over several periods of the vibration.During the first test campaigns,for tests 1 to 13 and 18 to 20(see Table 1),the velocity of the outer steel plate is determined by using the measurement of one PDV signal.In case of the single plate (tests 14 to 17), the average of the initial velocity together with the mass of the plate determines the total impulse.During the last test campaign, for tests 21 to 26, it was decided to measure the velocity of the outer steel plate via three redundant PDV signals positioned at the same radial distance of 180 mm from the center of the rings, in order to determine a possible tilting of the outer steel plate, which was not found after measurements.

Fig.1.Ring technology device for the measurement of local specific impulse distributions (left) and single plate for the measurement of the total impulse (right).

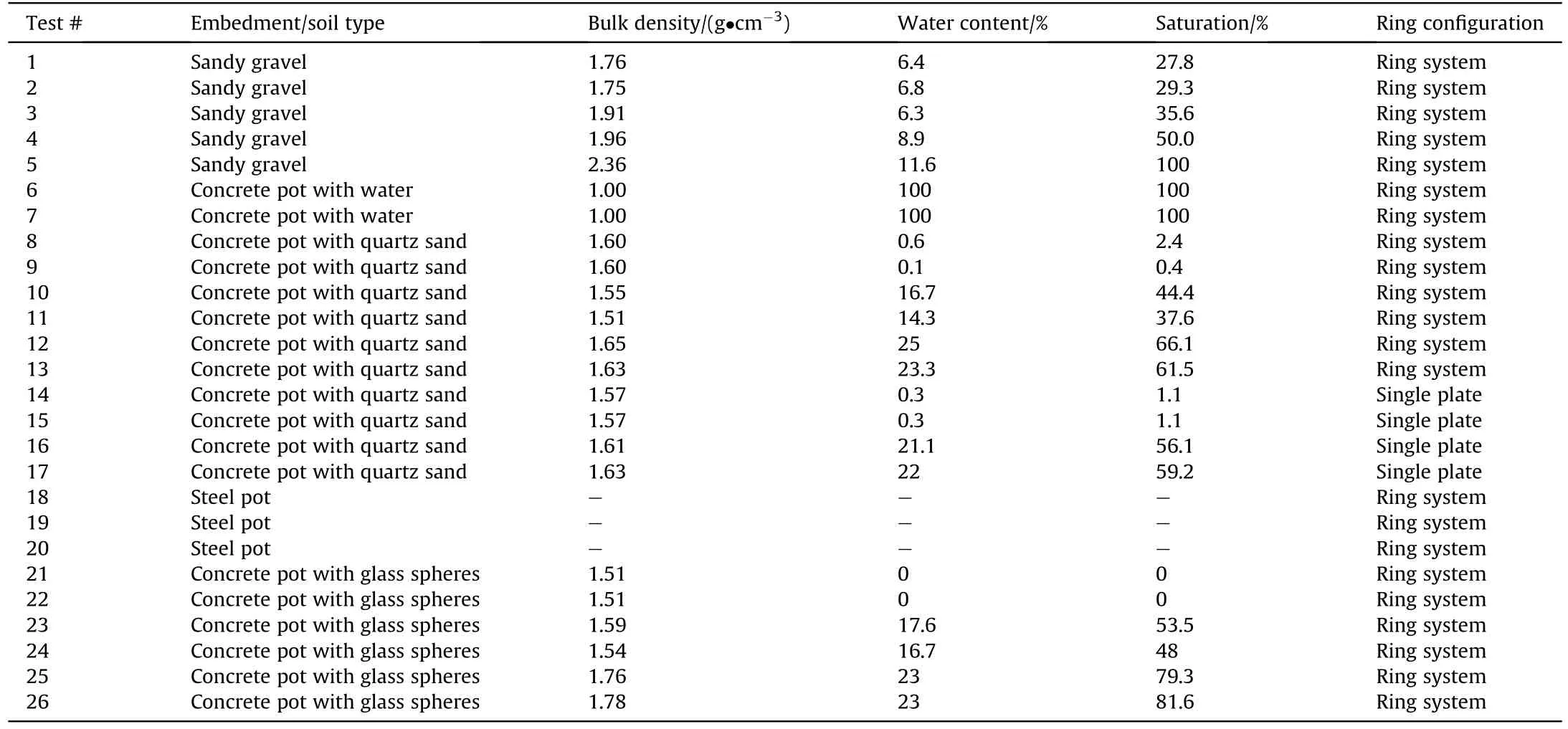
Table 1Test program and the corresponding embedding parameters.

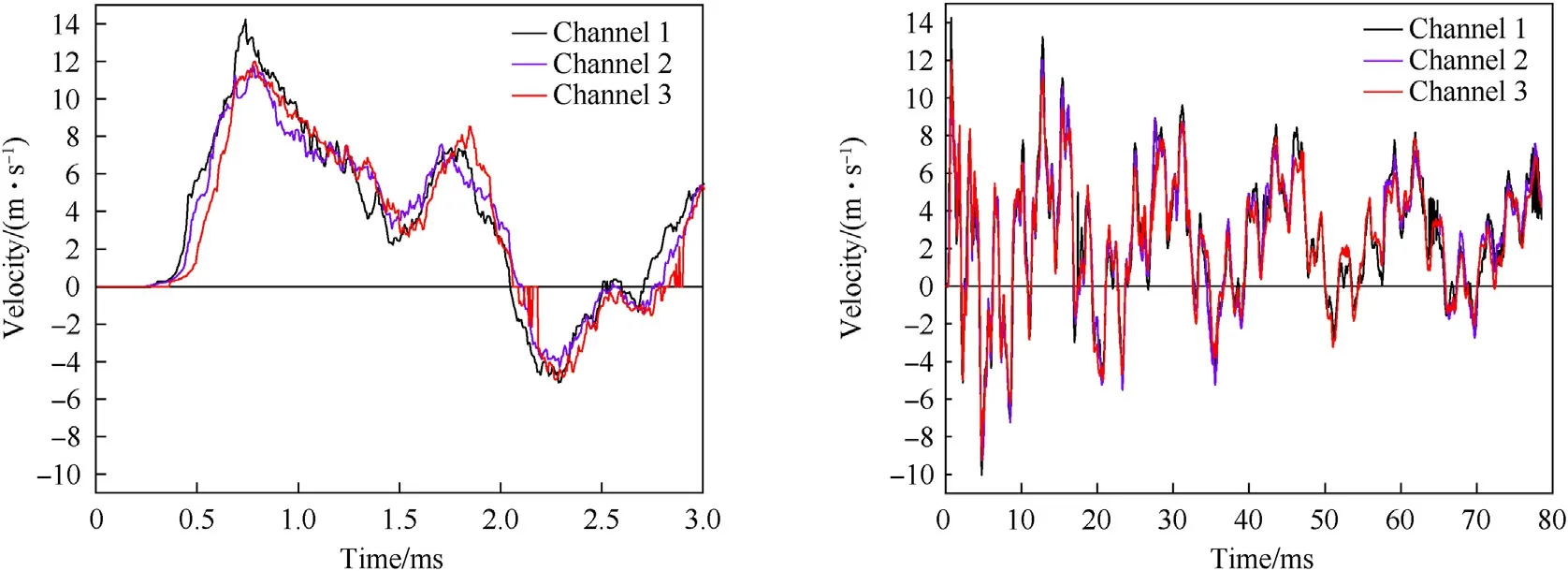
Fig.2.Velocity curve of the outer steel plate (ring 9), measured with three PDV channels, for test #26 (left: zoom).

In order to be able to compare these tests with previous ones,the HE charge is placed in a sand filled cardboard barrel of 63 cm diameter 80 cm height.A new barrel is used for each test.The PETN charge is of cylindrical shape and has a mass of 84 g with a diameter of 59.2 mm.The initiation of the charge occurs at the center of the bottom of the explosive charge, via Exploding Bridgewire Detonator RP501 or RP80, in order to obtain the detonation time to trigger the X-ray diagnosis.The distance between the top of the barrel and the ring structure or the single plate is 139 mm.More details on the experimental setup can be found in Refs.[14,15].

The result of the measurement of the velocity of the outer steel plate via the three redundant PDV signals positioned at the same radial distance of 180 mm from the center of the rings is shown exemplary in Fig.2 for test#26.

It was found that the standard deviations between the results of the three different PDV channels were very small.The maximum standard deviation was 7.1%for test#24,and for the other tests the standard deviation was below 2.6%, ensuring the validity of the measurement method.

3.Embedment configurations

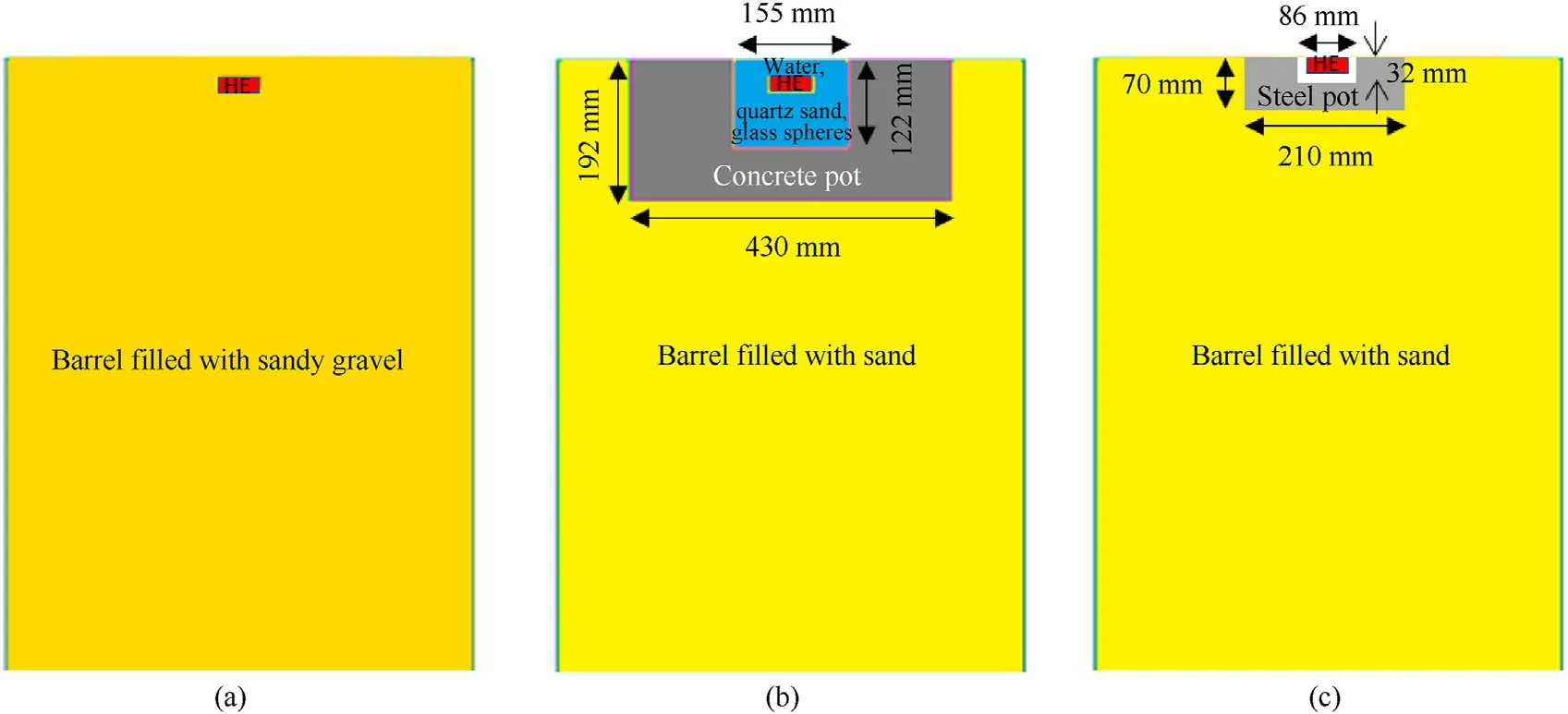
Fig.3.Embedment of the HE charge (a) In sandy gravel; (b) In a concrete pot filled with water, quartz sand or glass spheres; (c) In a steel pot.

The experimental configurations were used to analyze the influence of different embedments on the specific impulse distribution and on the total impulse.Four different alternatives to sandy gravel were tested: firstly, a concrete pot filled with water, secondly, a concrete pot filled with quartz sand of different water contents (0%, 15%, 25%), thirdly, a steel pot without filling and finally the HE was embedded in concrete pot filled with glass spheres with different water contents (0%,17%, 23%).The use of a concrete pot would help reduce the amount of material needed for the test compared to filling a 2 m×2 m test pit as required by AEP-55,Volume 2.Water was chosen because it is the same material all over the world, and quartz sand and glass spheres were chosen because of the homogeneity of their grain size, which should help to obtain a better reproducibility of the results, as opposed to the variability of the grain size observed for sandy gravel.The steel pot is already mentioned in AEP-55,Volume 2,as a surrogate mine and was therefore also tested.The geometry and dimensions of the four embedment types are shown in Fig.3.The internal dimensions of the concrete pot, a diameter of 155 mm and a depth of 122 mm,were designed using numerical simulations to provide similar impulses to that obtained with sandy gravel.To prepare the concrete pot,a casing was built.Cast concrete was then used for the body,a ready-mixed concrete with a strength of 35 MPa.The steel pot was made of structural steel St-52.An embedment in sandy gravel,used as a reference,was also studied.The grain size distribution of quartz sand and sandy gravel is given in Fig.4.82% of the quartz sand particles had a size of 0.1 mm-0.4 mm,with the largest grain size of 0.5 mm.Sandy gravel had a size fraction with significantly larger grains, up to 4 mm and corresponds to the STANAG sandy gravel according to the specification given in Ref.[1], scaled with a scale factor of 4.3.The scaled sandy gravel will be referred to as sandy gravel in the rest of the paper.As the thickness of the rings is 20 mm and to prevent big particles up to 40 mm(as specified for STANAG sandy gravel) from impacting two rings at the same time, it was decided to scale down the particle size of sandy gravel.The glass spheres used are frequently used for sandblasting.They had a bulk density of 1.5 g/cm3to 1.6 g/cm3comparable to quartz with 0%water content (1.5-1.6 g/cm3).100% of the glass spheres had a diameter between 200 μm and 300 μm.They had a specific gravity of 2.45 g/cm3,which was slightly lower than the specific gravity of quartz(2.641 g/cm3).The depth of burial is kept constant at 23 mm,except for the embedment in the steel pot, where the HE is positioned flush with the barrel level, as mentioned in the AEP-55,Volume 2.The concrete and steel pots were positioned in quartz sand (water content 0%) in the barrel.The ignition cable for the detonator was inserted from below with a pipe in the concrete or steel.The HE was placed in a plastic casing to ensure the correct depth of burial,this casing lying on the pipe to support the HE.The concrete pot was filled with a measured mass of dry sand, mixed with a measured mass of water to achieve the desired water content, and compacted.The bulk density was calculated after compaction by knowing the volume of the mixture.The quartz sand and glass spheres were manually compacted inside the concrete pot using a metal tamper, layer by layer.The embedment of the HE in the concrete and steel pot before detonation is illustrated by the photographs in Fig.5.A new steel pot, concrete pot and barrel was used for each test.

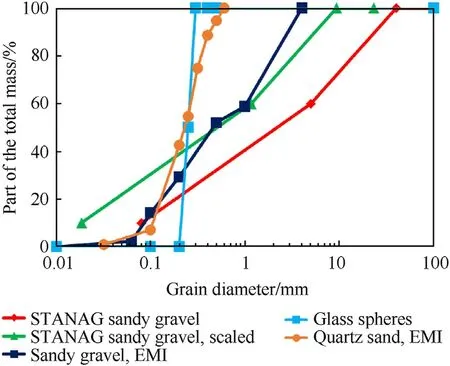
Fig.4.Grain size distribution for quartz sand and sandy gravel measured at the EMI,for glass spheres, for scaled STANAG sandy gravel and STANAG sandy gravel as specified in Ref.[1].

Fig.5.Illustration of experimental configurations: (a) Overview of the concrete pot;(b) Casing for the ignition; (c) Embedment of the HE charge in a concrete pot filled with quartz sand; (d) In a concrete pot filled with water; (e) In a steel pot; (f) In a concrete pot filled with glass spheres.

Table 1 shows a summary of the experiments carried out for sandy gravel and its four alternatives,measured via the ring system or via the single plate and provides the experimental parameters such as type of embedment, bulk density, water content and saturation for each test.To determine the water content, a sand sample was taken, dried and then the water content was determined via the mass loss.

4.Comparison with scaled sandy gravel

In order to quantify the potential of the different embedments as a replacement for sandy gravel, the specific and total impulses were compared with sandy gravel with a water content of 6% and 11% in Fig.6.An error analysis has been made, showing that the possible measurement error for the velocity was the same order of magnitude than the discrepancy observed between two tests with identical embedding conditions.The error bars, when presented,were therefore calculated using the standard deviations of the tests that had the same embedding conditions (for example, test #25 and #26, or tests#1, #2 and #3).

The maximum specific impulse of the charge in a concrete pot filled with water (8545 kg·m/s) was slightly lower than that in sandy gravel with a water content of 11% (9596 kg·m/s) and the total impulse showed comparable values for the concrete pot filled with water(535 kg·m/s)and an embedment in sandy gravel with a water content of 11% (581 kg·m/s).

Regarding the HE embedded in a concrete pot filled with quartz sand at a water content of 25%, it was observed that the specific impulses were very close to the values of sandy gravel with water content 11%, within the error bars of the tests.The maximum specific impulses for sandy gravel with a water content of 6%were below the quartz sand embedments for small radial positions.For large radial positions,the values of the quartz sand embedment in the concrete pot with a water content of 0%were close to the values of sandy gravel with water content 6%.The cumulative impulses for the concrete pot filled with quartz sand at a water content of 15%and 25% were located between the two sandy gravel curves.However, the total impulse for the concrete pot filled with quartz sand with a water content of 0% (292 kg·m/s) was slightly below the total impulse of the sandy gravel with a water content of 6%(352 kg·m/s).

Fig.6.Specific(top)and cumulative impulse(bottom)as a function of the radial position for different HE charge embedments.Comparison with the sandy gravel embedment(with a water content of 6%-11%).The error bars correspond to the standard deviations of the tests.

With an embedment of the HE in the steel pot, the maximum specific impulse(directly above the load)was about 10,400 kg·m/s,compared to 9600 kg·m/s and 5800 kg·m/s with sandy gravel at a water content of 11%and 6%,respectively.From a radial position of 110 mm, the specific impulse with the steel pot was smaller than the specific impulse with sandy gravel with a water content of 11%by a factor of approximately 2.The steel pot has a strong focusing effect, so that directly above the charge, both steel pot and sandy gravel can have a similar effect.In the case of a structure with a large surface area,however,an impulse applied radially further out also becomes significant.The total impulse obtained with sandy gravel cannot be reproduced by a steel pot.

It was found that up to a radial position of 160 mm the cumulative impulses for the embedment in a steel pot were between the two sandy gravel results.However, this changes significantly for positions further out.The total impulse,i.e.the cumulative impulse at the radial position of 600 mm(271 kg·m/s),was lower than the total impulse of the two sandy gravel embedments:581 kg·m/s for sandy gravel with 11%water content(factor 2)and 352 kg·m/s for sandy gravel with 6% water content.

It was observed that the specific impulses with the concrete pot filled with glass spheres at water content 23% were close to the values of sandy gravel with water content 11%.The maximum specific impulses for sandy gravel with water content 6% were below the other values for small radial positions.For large radial positions, the values of the concrete pot filled with glass spheres with water content 0% and 17% approached the curve for sandy gravel with 6% water content.

The cumulative impulses for the concrete pot filled with glass spheres with water content 17%and 23%were located between the two sandy gravel curves.The total impulse(cumulative impulse at 600 mm) for the concrete pot filled with glass spheres with 0%water content (297 kg·m/s) was slightly below the total momentum for the sandy gravel with 6%water content(352 kg·m/s).

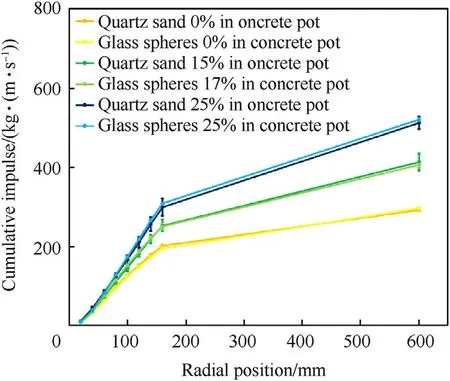
Fig.7.Comparison between the embedment in a concrete pot filled with quartz sand or with glass spheres.Cumulative impulse as a function of the radial position.The error bars correspond to the standard deviations of the tests.

The cumulative impulses with the concrete pot filled with glass spheres or with quartz sand are compared in Fig.7.It was found that at almost identical water content (0% for quartz sand and for glass spheres,15%for quartz sand and 17%for glass spheres,25%for quartz sand and 23%for glass spheres),almost identical cumulative impulses and total impulses were observed.Quartz sand and glass spheres (at water content 15%-25%) would be equally well suited to replicate sandy gravel experiments.

Both the maximum specific impulses and the total impulse showed comparable values for the concrete pot filled with water and for sandy gravel with a water content of 11%.Water embedded in a concrete pot would therefore be a suitable alternative to sandy gravel.According to these experiments,the steel pot would not be a sufficient substitute for sandy gravel, due to its strong focusing effect.Quartz sand and glass spheres (at water content 15%-25%)would be equally well suited to replicate sandy gravel experiments,as the maximum specific impulses and the total impulses were between those obtained for embedment in sandy gravel with a water content of 6% and 11%.

It is observed that there is a good agreement between the specific and cumulative impulses for wet materials (wet quartz sand and wet glass spheres, water) and sandy gravel, probably because their saturation ratios are similar, between 30% and 100%.On the contrary,materials with a saturation close to 0%,such as dry quartz sand, dry glass spheres and steel pot, do not show a good agreement.

5.Tests with single plate

Four tests were carried out with the single plate to quantify possible effects such as friction or loss of impulse due to flow between the rings for dry and wet sand.The total impulse measured either with the ring system or with the single plate is shown in Fig.8.The agreement between the two measurement methods was very good in each case.

For the dry sand(water content 0%)the total impulse measured with the plate was approximately 12%higher than the total impulse measured with the ring system.A t Student test for dry sand gives a p-value of 0.007 which is below 0.05, indicating a statistically significant difference between the ring system and single plate tests.In the case of dry quartz sand, it could generally be possible that some of the sand particles are ejected through gaps between the rings,thus reducing the total impulse.A previous test series where a high-speed camera was placed in front of the ring system showed that a small amount of sand particles could be observed between some of the rings.

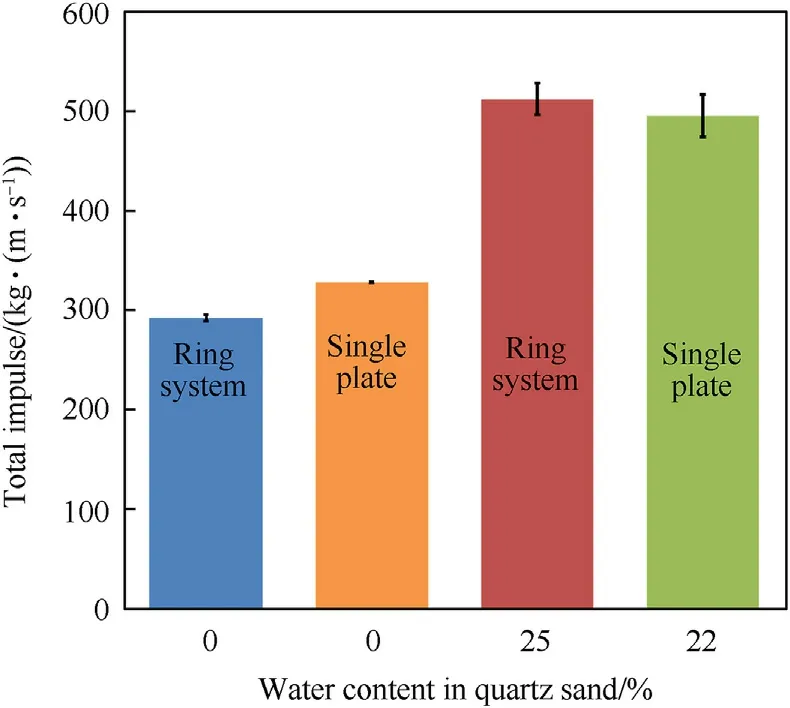
Fig.8.Total impulse measured with ring system and single plate, at different water contents in the quartz sand.The error bars correspond to the standard deviations of the tests.

Fig.9.Numerical simulation model of the detonation with ring system, depth of burial 23 mm.Left: HE placed in a sand barrel.Right: HE placed in a filled concrete pot.

For the wet sand the total impulse measured with the plate was approximately 3%lower than the total impulse measured with the ring system,probably because the water content of the single plate tests(22%)was lower than that of the ring system(25%).A t Student test for wet sand gives a p value of 0.5907 which is greater than 0.05,indicating nevertheless that there is no statistically significant difference between the ring system and single plate tests.

This comparison confirmed that the measurement with the ring system is very well suited to measure the total impulse.Deviations due to friction or sand ejected between the rings seem to play only a minor role.

6.Numerical simulation with a model considering soil moisture

6.1.Simulation model

A numerical model was used to simulate some of the tests previously investigated.For these simulations the finite-element software tool Autodyn was chosen.The embedment of the HE in the concrete pot and the air were represented with a Euler model,which is appropriate to compute large deformations and to study the properties of fluids.The steel rings were modelled using a Lagrangian model, as they are not subjected to large deformations and there is a need to track their motions.A fluid-structure coupling was applied.The HE detonation itself exhibits a 2D symmetry,which can be exploited to simulate the detonation with high accuracy in a 2D model.The element size was 3 mm.

For the numerical simulations, material descriptions of the following materials are necessary:for quartz sand,sandy gravel and glass spheres,the model of Laine&Sandvik[4](at a soil density of 1.67 g/cm3and a water content of 6%),which includes a compaction curve and a pressure-dependent strength description, or a model considering soil moisture, as described in the next paragraphs,were used.The concrete pot was modelled with the RHT model[20]with a compressive strength of 35 MPa.Regarding the high explosive PETN, a JWL equation of state, with a density of ρPETN=1.54 g/cm3had been chosen.For air,the equation of state for ideal gas was used.An elastic-plastic model with strain hardening described the steel rings and the single plate.

The numerical model is shown in Fig.9 for an embedment of the HE in a sand barrel or in a filled concrete pot.

6.2.Numerical model considering soil moisture

As observed in Table 1, the tests exhibited a large variation of water contents and saturation.The sand model from Laine &Sandvik is available for a water content of 6%.In order to model tests with high saturation levels, there is a need for a numerical model considering soil moisture.

For this soil model, a three-phase model is used, based on the results of Aurich [21] and Marrs [5].It includes: a solid phase(mineral particles),a liquid phase(water)and a gaseous phase(air).The void space between the particles can be, either completely filled with air, completely filled with water or a mixture of air and water.The composition of the soil for different saturation levels is shown as an example in Fig.10.

Fig.10.Three-phase sand model.Left:void space filled with air (saturation 0%).Middle:void space filled with water and air.Right:void space filled with water(saturation 100%)[21].

For the present study,it was decided to follow the methodology of Marrs [5] and Fiˇserov'a [6].The methodology was described in detail in Ref.[5].However, for completeness and better understanding,it is revised again here using an application example(test#4, sandy gravel, water content 8.9%).

In order to determine the compaction curve and the yield strength of a special sand-water mixture with this sand model,the bulk density(wet density)and dry density are taken directly from the tests.These densities are used to calculate the water content,void ratio,porosity and saturation using the following formulas.

· water content ω:

where ρdis the dry density,ρ the bulk density,

· void ratioe:

where ρsis the grain density of the solid material (for sand ρs= 2641 kg/m3),Va,Vw，Vsthe partial volumes of air, water and solid material.

· porosityn:

· saturationS:

where,ρwrepresents the water density and has the value ρw=1 g/cm3.

The porosity and saturation values were then used to calculate the values of the initial relative volumes of air, water, and solid material, respectively, using the following formulas:

Initial relative volumes of air, waterand solid material:

The relative volumes of air and water under pressure (und） were calculated using their equations of state as follows:

Withpthe pressure,ka=1.4,kw= 3,p0= 0.1 MPa (empirical values) andcwthe speed of sound in water(cw= 1414 m/s) [5].

The equation of state of the solid material is not known,but it is assumed that the relative volume of the solid material under pressure has the following form:

For a compaction pressurep=0 MPa the following is obtained:

6.3.Compaction curve

The first compaction occurs along the compaction curve until the line of fully compacted material(saturated sand-water mixture)is reached.After the material is fully compacted, there is a linear relationship between pressure and density (see Fig.11).The calculation of the linear elastic sound velocitycTMD(TMD = theoretical maximum density) is done according to Eq.(21).

The density ρpof the sand-water mixture under pressure is calculated until the line of fully compacted material as follows:

An essential aspect in the modelling is the consideration of the state of full compaction (pores completely filled with water).The line of the fully compacted material was obtained by calculating the density at zero pressure of the theoretical maximum density and the bulk modulus at the theoretical maximum density.

The density at zero pressure of the theoretical maximum density ρTMDcan be calculated from a volume-weighted average of the densities of water and solid material:

The bulk modulusKTMDon the line of the fully compacted material is constant and is calculated from:

whereKwis the bulk modulus of water,Kw= 2.16 GPa andKsthe bulk modulus of the solid material,Ks= 56.7 GPa, obtained from the work from Laine and Sandvik [4,5].

The line of the fully compacted material cannot be crossed.The relationship between the density ρiand the pressurePion this line is described by the following formula:

where:

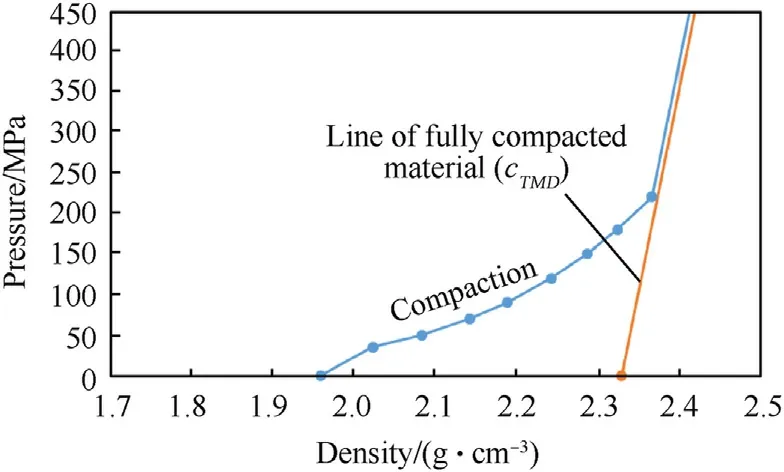
Fig.11.Compaction curve using the example of sandy gravel, water content 8.9%.

The calculation of the compaction curve for the different densities proceeded as follows.First, ten pressure data points were selected.The constitutive equations for volume fraction were applied to determine the relative volume fractions of the solid material, air and water at each of the ten pressures.Then the density was calculated for each of the ten pressures.Each point was checked to ensure that it was to the left of the line of fully compacted material.If a density was above this line, the pressuredensity relationship was adjusted so that the curve was parallel to the line of fully compacted material.

The bulk moduliKiwere calculated as a function of pressure and density from the definition of bulk modulus:

The shear modulusG, was calculated as a combination of the Poisson’s ratio and the bulk modulus:

The volumetric strains and the linear elastic sound velocities as input parameters were calculated with the following formulas.

· volumetric strain εi:

· linear elastic sound velocityci:

A typical compaction curve as a function of volumetric strain is shown in Fig.12.

6.4.Yield strength

For the yield strength, the model of Laine and Sandvik [4] was modified.The yield stressYcan be determined linearly with the following formula, up to a maximum at 226 MPa (maximum strength of sandstone and estimated maximum strength of the soil particles):

With the friction angle φ,rad;the cohesionc,MPa;the pressureP, MPa.

The friction angle is determined with the following formula:

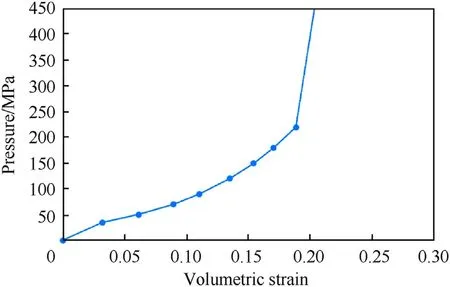
Fig.12.Compaction curve as a function of volumetric strain, using the example of sandy gravel, water content 8.9%.

where ϑ is the Poisson’s ratio of the soil.

The Poisson’s ratio ϑ was varied with the water content from the sand-water mixture using the relative volume approach:

The following values were assumed for the Poisson’s ratios of water ϑw, air ϑaand the sand particles ϑsaccording to Refs.[4,5]:

ϑs=0.222.For the cohesionc,MPa;the following formula from Grujicic [22] was used:

where ω stands for the water content of the soil.

For our example, the yield strength curve is shown in Fig.13.

The consideration of moisture in the model is illustrated using the example of three saturation levels (0%, 50% and 100%) on the basis of their compaction curves as a function of volumetric strain on the left in Fig.14.It was found that the increase of saturation causes a shift of the compaction curve to the left.Since the saturated soil is already fully compacted, it cannot be compacted further.

6.5.Comparison with the model of Laine and Sandvik

Test #4 (sandy gravel, depth of burial 23 mm, water content of 8.9%, saturation 50%) and test #5 (sandy gravel, depth of burial 23 mm, water content of 11.6%, saturation 100%) were simulated with the model of the soil with consideration of the moisture and with the model from Laine and Sandvik in Fig.15 for comparison.

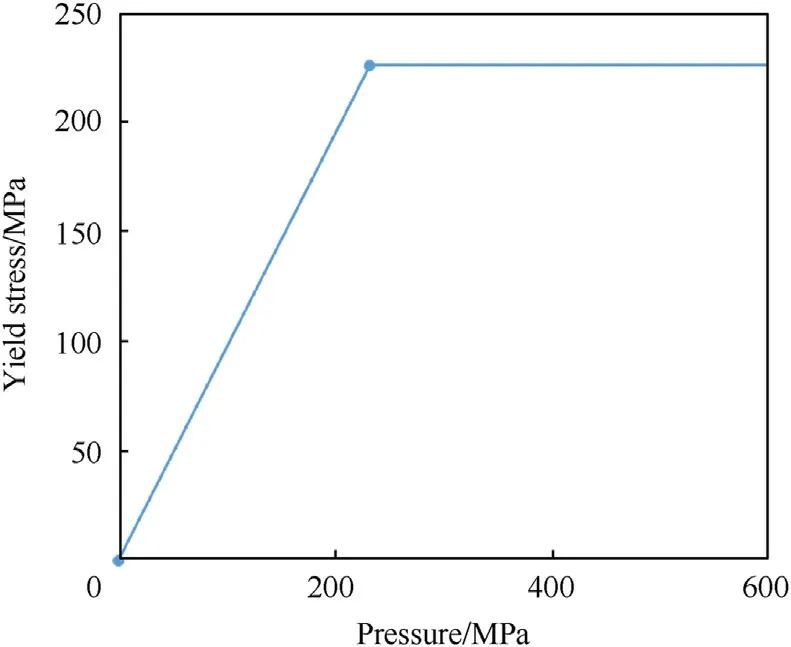
Fig.13.Yield stress as a function of pressure,using the example of sandy gravel,water content 8.9%.

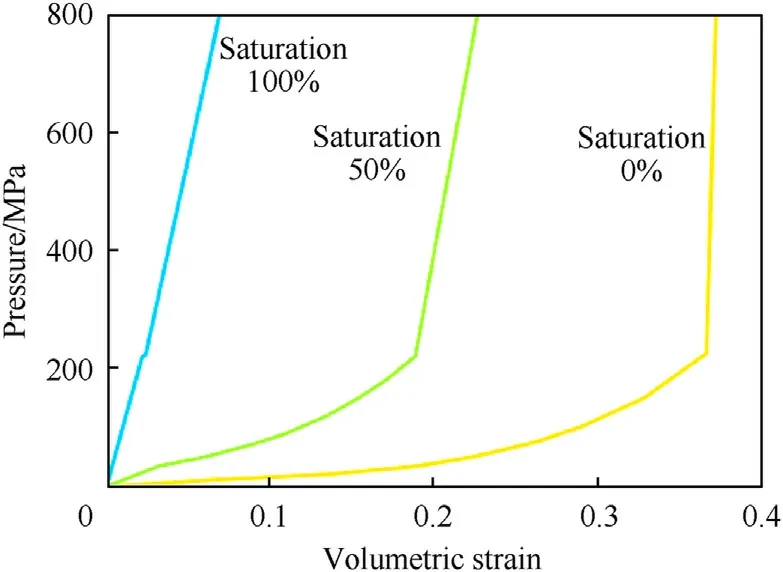
Fig.14.Compaction curves for sand with different saturation ratios.

It was observed that the model used here,which takes moisture into account, is as expected much better at representing higher saturation ratios than the Laine&Sandvik model,which is a model where only a constant water content of 6%can be used.At both 50%and 100% saturation, there was very good agreement between the experimental and simulation curves, validating the model.

In contrast, the Laine & Sandvik model predicted only half (at 50% saturation) to two-thirds (at 100% saturation) of the total impulse.

6.6.Simulation of the experiments with the glass spheres

The experiments carried out with glass spheres were simulated with the same model considering soil moisture,as the glass spheres had similar water content and particle size to quartz sand.Three water contents were calculated:0%(tests#21 and#22),17.6%(test#23) and 23% (test #26).Unlike quartz sand and sandy gravel(where ρs=2.641 g/cm3),here ρs=2.45 g/cm3was taken from the product data sheet for the glass sphere particle density (without pores).The compaction curve, which describes the relationship between density and pressure,is shown in Fig.16.The curve starts at the initial density(bulk density)of the glass sphere mixture.The dashed curves represent the asymptotes corresponding to the fully compacted materials at the different water contents.A similar displacement of the compaction curve to the left for increasing saturation ratios has been observed in the work of Arlery et al.[23].The yield stress as a function of pressure is shown for the different water contents of the glass sphere mixtures in Fig.17.The results of the different simulations are shown in Fig.18.

Fig.15.Comparison simulation - experiment for embedding the load in sandy gravel, depth of burial 23 mm.(a) Water content 8.9%, saturation 50%, (b) Water content 11.6%,saturation 100%.Left: specific impulse as a function of radial position.Right: cumulative impulse of the rings as a function of radial position.

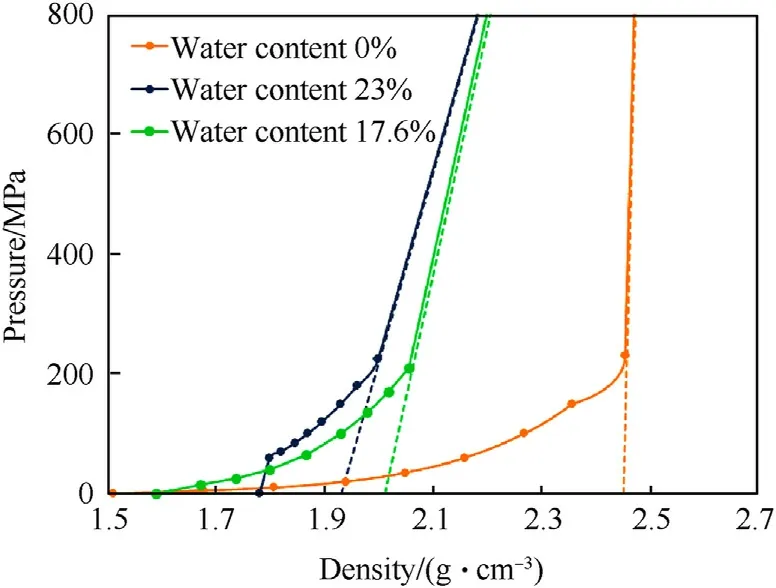
Fig.16.Compaction curves as a function of density for different glass sphere-water mixtures (0%,17.6% and 23% water content), according to the model used here.

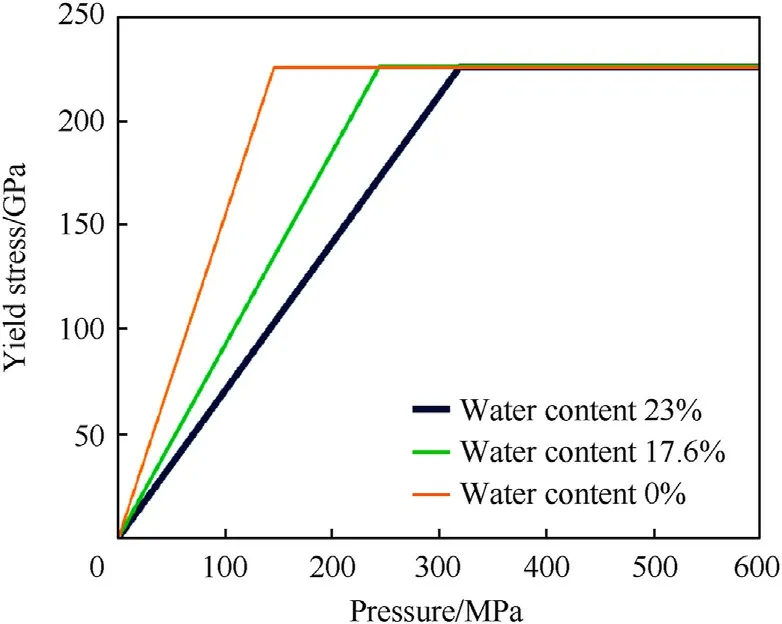
Fig.17.Yield stress of the different glass sphere-water mixtures (0%, 17.6% and 23%water content), according to the model used here.

It was found that the maximum specific impulses directly above the charge at the water content 17.6% and 23% in the simulation were significantly higher than the values from the tests.After a radial position of 70 mm,the experimental values converge in both cases.For the water content 0%, the simulation values agree well with the test, also for the maximum specific impulse.For the cumulative impulses, it was observed that at water contents 0% and 17.6%, the simulation curves almost overlap with the test curves.Even the total impulse (cumulative impulse at 600 mm) could be predicted very well at the water contents of 0% and 17.6%.At the water content of 23%, the total impulse in the simulation was 16%below the value of the experiment and the cumulative impulses up to a radial position of 100 mm were about 15% above the experimental values.

In general,it could be observed that the simulations agreed well with the experiments up to a water content of 17.6%.The simulation reproduced the increase in cumulative impulse in the same proportion as in the experiment.The model presented here could also be successfully applied to glass sphere-water mixtures.However,a possible limitation of the model is the validity of the derived yield strength curve of quartz sand for the simulation of other soil types.Another interesting investigation would be to check the ability of the numerical model to be used in a 3D blast simulation involving a vehicle.

7.Conclusions

An experimental setup was used to determine the local specific impulse ant the total impulse.It consisted of eight concentric rings,an outer steel plate placed on top of a barrel with a HE placed in an embedment.It improved the work of Fourney and Ehrgott by allowing the measurement of the specific impulse with good resolution and of the total impulse at the same time.Compared to a similar test setup from Rigby, where the instrumented region was limited to 100 mm, it was extended here to 600 mm.

For comparison with the ring system, another experimental setup was used with a single plate of the same diameter.

Four different alternatives to sandy gravel were tested:firstly,a concrete pot filled with water, secondly, a concrete pot filled with quartz sand of different water contents (0%, 15%, 25%), thirdly, a steel pot without filling, and finally, the HE was embedded in a concrete pot filled with glass spheres.

Both the maximum specific impulses(responsible for deflection during an explosion under a vehicle floor) and the total impulse(responsible for vehicle movement)showed comparable values for the concrete pot filled with water and for sandy gravel with a water content of 11%.Water also has the advantage to be identical all over the world, avoiding the discrepancy that could be observed in the grain size distribution of two different soils.

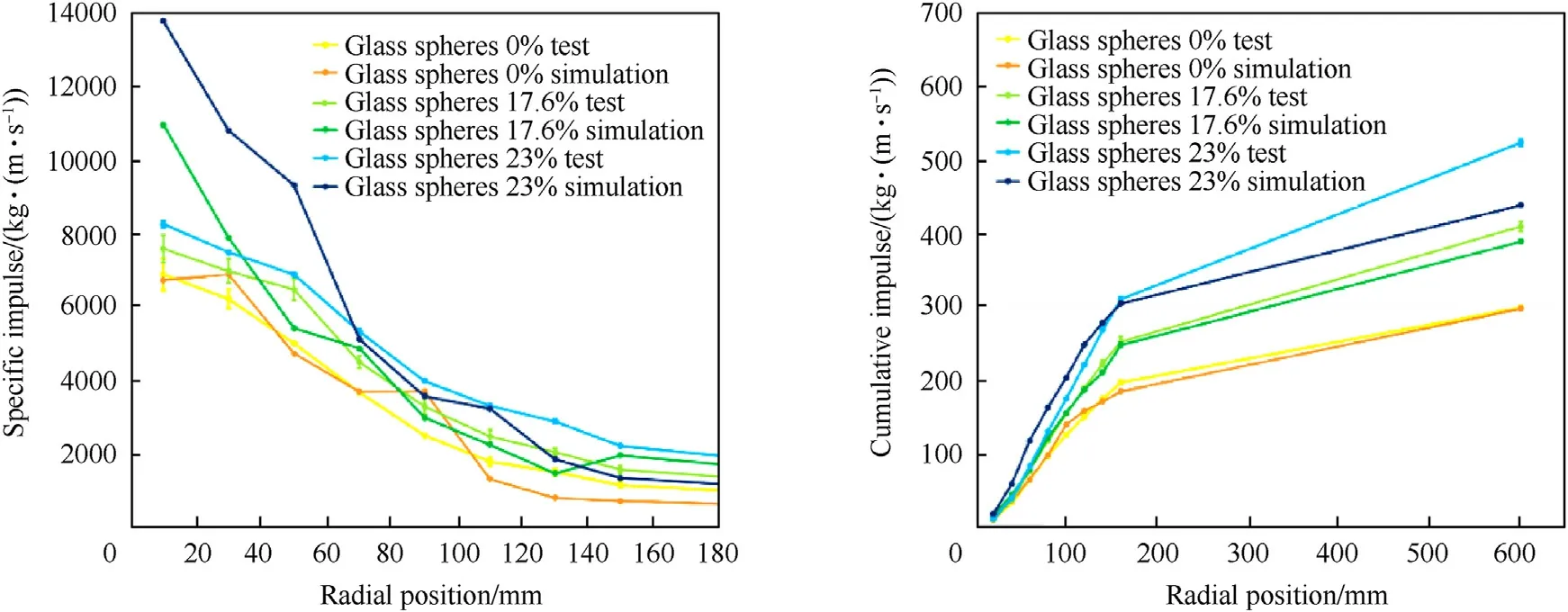
Fig.18.Specific(left)and cumulative impulse(right)as a function of the radial position.Simulation and tests with different glass sphere-water mixtures(0%,17.6%and 23%water content).Model considering the soil moisture.

The steel pot also has a strong focusing effect on the vehicle floor, so that directly above the HE both embedding methods can have a similar effect.In the case of a structure with a large surface area,however,an impulse applied radially further out also becomes significant.The total impulse obtained with sandy gravel cannot be reproduced by a steel pot.According to these measurements, the steel pot would not be a sufficient substitute for sandy gravel.

The configurations with the concrete pot filled with quartz sand with a water content of 15%or 25%and with the concrete pot filled with glass spheres with a water content of 17% or 23% would be well suited to represent sandy gravel tests,as the maximum specific impulses and the total impulses were between those obtained for embedment in sandy gravel with a water content of 6% and 11%.Quartz sand and glass spheres (at water content 15%-25%) would therefore be equally well suited to replicate sandy gravel experiments.However, the price of glass spheres (about 1.5 €per kg) is twenty times higher than that of quartz sand, which is more in favor of the latter.

A statistical comparison between the experimental setup with either the ring system or the single plate confirmed that the ring system measurement is very well suited to measure the total impulse.

A numerical soil model considering the soil moisture based on the work of Marrs and Fiˇserov'a was used to simulate the experiments at different water contents.The results of numerical simulations with this model are in much better agreement with the experiments compared to the classical Laine&Sandvik model with a constant water content for saturation levels up to 100%.It was also used to model successfully the soil with glass spheres with water contents from 0% to 23%.

With the idea of limiting the amount of material needed for the tests thanks to the concrete pot,these experimental and numerical results can be used to develop new full-scale test conditions that are more reproducible,easier to handle and cheaper than the actual tests performed with STANAG sandy gravel.

To fully evaluate the potential of these possible alternatives to sandy gravel(water,quartz sand,and glass spheres in the concrete pot), it would be interesting to measure the deflection and deflection velocity of a steel plate positioned on the sand barrel,as described in AEP 55 vol 2.In this way, full-scale steel plate tests with large test rigs could be verified by smaller scale models.

The relationship between impulse and deflection could thus be determined.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The authors want to thank the Bundeswehr Technical Center for Weapons and Ammunition WTD-91 GF-440 in Meppen, Germany for funding this work.