GNSS观测值类型对短基线大地高差精度的影响分析
王恒毅,谭荣杰,杨瀚融,陈华
( 1. 武汉大学测绘学院, 武汉 430079;2. 内蒙古自治区测绘地理信息中心, 呼和浩特 010051 )
0 引言
利用GNSS获取高精度大地高,再结合似大地水准面模型确定水准高程已经成为了一种新的水准高程测量模式[1]. 我国许多城市都建立了精度优于±1 cm的似大地水准面模型[2]. 利用GNSS确定高精度大地高差,成为了实现水准高程传递的关键. 对于长度不超5 km的短基线,GNSS能测定毫米级精度的大地高差. 然而,GNSS提供多个频率的观测值,这些观测值及其线性组合的相位中心偏差改正和噪声均不相同. 研究不同的观测类型对短基线大地高差精度的影响对GNSS高精度定位和水准高程快速测定具有重要价值.
目前围绕观测值类型对短基线处理精度的影响已经有了较多的研究,有研究基于仅约数米的超短基线开展实验验证,认为短基线采用单频观测值的结果优于双频无电离层组合观测值,而采用双频原始观测值进行相对定位精度更高[3-4]. 还有研究指出对于大于5 km的基线,需要采用无电离层组合观测值来削弱残余电离层的影响[5-6]. 这些实验中大多采用的是仅为数米基线的数据,且大多均是从基线分量中误差、重复基线较差等角度进行结果评估. 本文采用数条长度为1~3 km的基线数据开展实验,并联合二等水准观测结果以及高精度的似大地水准面模型来评估大地高的精度,以此来分析不同GNSS观测数据值对短基线定位,尤其是对短基线大地高差测量的影响.
1 短基线定位模型与大地高精度评估方法
1.1 短基线定位模型
双差载波相位观测模型是短基线相对定位中常用的方法. 该模型将载波相位观测值在站间和星间进行了两次差分,消除了接收机和卫星钟差,削弱了卫星星历误差和大气延迟等具有强空间相关性的误差,其观测方程可以表达为
式中: Δ∇ 为双差算子; λ 为载波波长,大小与所采用的相位观测值类型有关; Δ∇φ˜ 为双差载波相位观测值; Δ∇ρ 为双差几何距离; Δ∇N为双差整周模糊度;Δ∇Vion和 Δ∇Vtrop分别为双差后的电离层延迟和对流层延迟误差,在短基线中一般假设该项可忽略不计[7].
1.2 基线大地高差精度评估方法
本文主要采用三种方式来评估基线大地高差的精度:一是重复基线大地高差较差;二是基线向量的中误差;三是联合二等水准和似大地水准面模型计算出基线大地高差的参考值,再进行对比分析.
重复基线大地高差较差就是同名基线两个时段大地高差计算结果的差值,即
其中: Δ∇H是不同观测时段高程方向的较差;ΔHses2与 ΔHses1分别表示第2个时段和第1个时段基线高程方向的分量. 通过对比不同基线解算策略的大地高差较差,可以分析不同解算策略的大地高差测量精度和稳定性.
联合二等水准和似大地水准面模型计算出基线大地高差的参考值. 通过二等水准获得两点间的正常高差,利用似大地水准面模型可确定两点间的高程异常之差. 由此,可确定基线的大地高差,如式(3)所示:
式中: ΔH为GNSS短基线相对定位得到的基线两端大地高之差; ΔH正常为二等水准测量得到的基线两端的高差; Δξ 为通过似大地水准面模型得到的高程异常之差. 实验所采用的高精度似大地水准面模型精度为7 mm,由误差传播定律可知联合二等水准测量和似大地水准面模型得到的大地高差精度接近10 mm,说明参考值精度较高,故可以将其作为检验基线解算高程精度的指标.
2 实验数据处理
本文的实验数据为我国某市C级网2018年的双频观测数据,所有测站的接收机类型均为Trimble R8.实验所观测的基线数量为10条,基线长度均小于3.5 km. 每条基线都进行了2个时段的观测,每个时段观测时长为4 h.
实验所采用的基线解算策略包括四种:
1)仅使用双频接收机中L1载波相位观测值进行基线解算的策略,设为L1_ONLY;
2)仅使用双频接收机中的L2载波相位观测值进行基线解算的策略,设为L2_ONLY;
3)同时使用L1和L2载波相位观测值的基线解算策略,设为L1,L2_INDEPEND;
4)使用由L1和L2组成的无电离层组合观测值进行基线解算的策略,设为L1,L2_IF.
其他与基线解算有关的参数设置如表1所示.
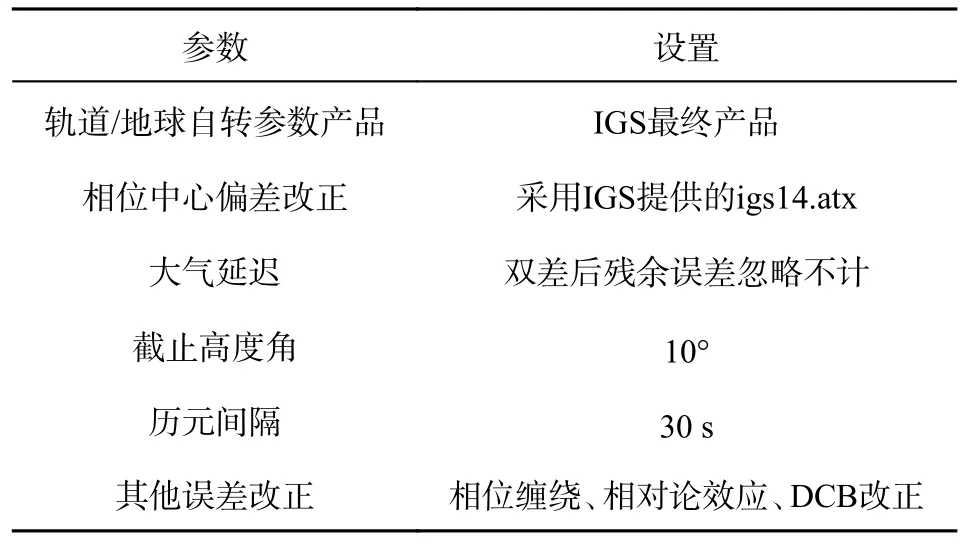
表1 基线解算设置
实验先按照四种解算策略依次对基线进行处理,并在得到各时段基线向量在E、N、U三个方向的分量大小和中误差后,计算出所有同名基线分量的重复基线较差. 同时,结合式(3)计算出联合二等水准高程测量结果和似大地水准面得到大地高差参考值,并将短基线相对定位得到的大地高差与之对比分析.
3 结果分析
3.1 重复基线较差
将同名基线2个时段的解算结果作差,得到了四种策略下各条基线向量在N、E、U三个方向分量的重复基线较差,其结果如图1所示.
根据图1可以发现,除了一条长度约1.6 km的基线部分解算策略的重复基线较差接近1 cm外,其余基线四种解算策略的重复基线较差均在1 cm以内,且所有基线的重复基线较差均符合C级网的测量规范要求,这表明两个时段的基线测量结果重复性较好,基线质量较高. 此外,不同基线解算策略得到的结果在高程方向上的重复基线较差无明显差异,难以据此比较不同解算策略间大地高差测量精度的差异.因此,通过分析重复基线较差可以看出基线测量的内符合精度较好,但要判断不同基线解算策略的精度,还需进一步分析.
3.2 基线分量中误差分析
将各时段的基线分量中误差依照误差传播定律计算得到各条基线的N、E、U三个方向分量的中误差,计算结果如图2所示.


图2 四种解算策略E、N、U方向分量中误差
观察图2可以发现,所有策略U方向分量的中误差显著高于N和E方向的中误差,这表明GNSS短基线相对定位在高程方向上的定位精度要低于平面定位精度.
同时,对比四种解算策略可以发现,L1,L2_IF在三个方向的中误差均显著高于其他解算策略,这是由于无电离层组合观测值消除电离层延迟的同时,放大了原始观测噪声[8-9]. 而在短基线相对定位中,电离层延迟已通过站间和星间差分被显著削弱. 相较于其他三种解算策略,L1,L2_IF消除电离层延迟的优势无法体现,但放大观测噪声的缺点仍然存在,从而导致解算精度低于其他解算策略.
此外,由于L1,L2_INDEPEND使用了L1和L2两个频率独立的载波相位观测值,相当于在单频相位观测值的基础上增加另一个频率的独立多余观测,因此其三个方向分量的中误差在四个解算策略中最小.
3.3 联合二等水准和似大地水准面模型的大地高差精度分析
利用当地城市级±1 cm的似大地水准面模型和二等水准测量成果,根据式(3)计算得到的各基线的大地高差的参考值,将2个时段基线的加权平均值与参考值作差,所得结果如图3所示.

图3 四种解算策略大地高差与参考值之差
对比四种基线解算策略下各条基线大地高差与参考值之差的曲线可以发现,差值的变化与基线长度的关系并不显著,采用无电离层组合观测值的L1,L2_IF差值曲线显著高于其他策略,而采用双频独立相位观测值的L1,L2_INDEPEND差值曲线处在采用单频相位观测值的L1_ONLY与L2_ONLY的曲线之间.
同时,本文还统计了四种基线解算策略下各条基线大地高差与参考值之差的平均值和标准差,其结果如表2所示.
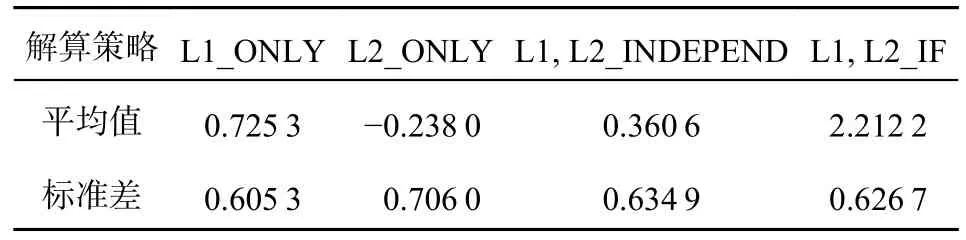
表2 四种解算策略大地高差与参考值之差的平均值及其标准差cm
结合图3与表2所示的计算结果可以发现,L1,L2_IF所得大地高差与参考值之差明显大于其他解算策略,且平均值高于其标准差的3倍,这说明L1,L2_IF的大地高差测量结果存在近2.2 cm的系统性偏差. 考虑到四种解算策略的差值与基线长度无明显相关性,说明二次差分后的大气残差对3.5 km以内的基线影响较小,进而说明使用该系统性差异与与大气延迟可能关系不大. 同时,L1_ONLY,L2_ONLY,L1,L2_INDEPEND这三种解算策略的差值数值十分接近,且曲线走势完全一致,各条基线间平均值的差距大于其标准差,说明三种基线解算策略的大地高差测量结果亦存在系统性偏差. 由于实验采用的是一体机Trimble R8,这种系统性偏差很可能与平均天线相位中心(phase center offset,PCO)的稳定性以及瞬时相位中心变化(phase center variation,PCV)等有关[10].
此外,通过对比三种解算策略的平均值和标准差可以发现:L1_ONLY测量结果标准差较小,测量精度较稳定,但测得的大地高差与参考值差异的平均值为0.7 cm;L2_ONLY则恰恰相反,其测得的大地高差最接近真实值,但其标准差为±0.7 cm,大于L1_ONLY,这可能与GPS L2信号的锁定方式有关;而L1,L2_INDEPEND由于同时采用L1和L2独立载波相位观测值,在测量准确度较高的同时,其测量精度也较稳定. 因此,在使用GNSS双频接收机进行短基线的大地高差测量时,基线解算策略建议优先选取L1,L2_INDEPEND,而不宜使用L1,L2_IF.
4 结 语
本文研究了不同GNSS观测值类型对短基线大地高差的影响,基于某城市C级网的观测数据,采用L1_ONLY、L2_ONLY、L1,L2_INDEPEND、L1,L2_IF等四种策略进行了计算,并从基线较差、基线分量中误差以及联合二等水准测量和似大地水准面模型检验方法等三个方面进行了分析,结果发现:
1)四种解算策略的重复基线较差均小于1 cm,说明实验所用基线质量较好,实验结果可靠性较高,也说明仅通过重复基线较差难以直接评估解算策略的基线处理精度.
2)实验中四种基线解算策略基线分量中误差与基线长度关系不明显,说明二次差分后的大气残差对短基线大地高差测量影响较小. L1,L2_IF结果中,基线分量中误差显著高于其他解算策略,这主要与无电离层组合放大了观测噪声有关.
3)与联合二等水准测量和高精度似大地水准面模型计算的基线大地高差结果相比,L1,L2_IF出现了接近2.2 cm的系统性偏差,明显大于其他三种策略,这可能与实验采用的Trimble R8一体机PCO的稳定性以及PCV有关. 因此,综合考虑基线中误差、重复基线较差等因素,建议使用GNSS双频接收机进行短基线大地高差测量时,可优先考虑使用L1,L2_INDEPEND策略进行基线解算.

