新疆昌吉地区降水空间分布特征研究
赵 华
(昌吉水文勘测局,新疆 昌吉 831100 )
降水量空间分布研究是气象科学领域热点之一[1]。目前降水量模拟主要使用数值模式,但由于气象观测站点限制,其在降水量时空分布方面模拟精度较低[2-3]。为了克服这一限制,学者们使用卫星遥感技术来获取高时空间分辨率的降水量数据,并证实了能够更准确了解降水量分布式信息[4-5]。然而,由于卫星数据分辨率通常比观测站粗糙得多,因此需要使用降尺度方法来将卫星数据转换为精细栅格面数据。目前主要的降尺度方法包括统计降尺度方法、动态降尺度方法[6-7]。动态降尺度方法通过分析大气-陆地系统之间的交互作用来降尺度,而具有较大研究成本。以随机森林回归算法为代表的机器学习方法不仅能预测降水量空间分布,同时也能够有效地降尺度卫星数据。
1 区域环境和研究方法描述
1.1 昌吉州地理环境
昌吉州位于亚洲大陆核心、我国新疆北部,总面积面积为11.2 万km2。区域东部为准格尔盆地区,西南侧为天山山麓,总体地势呈现自西向东、自南向北倾向,海拔介于227 m~5323 m 之间,形成高寒山地、隔壁、盆地绿洲等地貌。该地区属于温带大陆性干旱区,具有干旱少雨、酷暑寒冬、昼夜温差大等特点;年平均气温在6℃~12℃之间, 年降水量100 mm~300 mm,积温约2500℃,日照时数为2660 h,干旱日数约250 d,太阳辐射量120 kcal/cm2以上。该地水资源主要来自于天山融雪和地表径流,年径流量为33.7 亿m3。
1.2 降水数据介绍
从气象科学数据中心(http://data.cma.cn/)共收集到研究区16 个站点资料,时间为2020 年。该气象站点通过降雨量自记录仪记录雨滴时的微弱电信号进行降水测量。人工观测则在定点场地安装雨量计,由专业人员采集记录雨水的信息,并采用自动算法、人工复核等方法,对于存在异常或偏差的数据进行修正或删除,因而数据可信度高。
研究区GPM 卫星降水数据则通过官方网站获取(https://gpm.nasa.gov/data/directory)。该数据产品为IMERG,时间分辨率为/月,空间分辨率为0.1°(约10km),利用累加法将逐月GPM 数据合成2020 年产品,进而与该地地貌雨量站资料匹配。
1.3 随机森林回归降尺度算法
随机森林回归(Random forest regression)是一种基于决策树(CART)的集成学习方法,它通过将多个决策树的预测结果进行平均或加权平均来得到最终的预测结果。集成学习方法可以降低单一模型的泛化误差,提升模型的稳定性和准确度。以海拔、经度、纬度和经纬度等环境属性作为随机森林回归模型的输入特征,以基于气象站点降水量数据为目标变量,构造的训练集为:T={(x1,y1), (x2,y2), …,(xn,yn)},其中xi∈X,n=16 为输入样本数量,yi∈Y,为地面降水量值,进而拟合降水—环境之间复杂非线性关系下:
式中:B={1,2…,B},表示CART 数据;b表示boostrap样本数;tb*为单一CART,K是第k个训练样本,包含目标变量(y)和协变量(x)的成对值[8]。
1.4 数据分析与处理
本研究使用ArcGIS 软件对文中空间数据进行预处理,降尺度模型构建与参数优化则在Rstudio 软件中实行。利用随机森林回归算法预测得到的降水量栅格点值y'为参考值,以地面观测站降水量y 为真值,计算决定系数(R2)、平均绝对误差(MAE)和均方根误差(RMSE),对昌吉地区降水量GPM 降尺度精度进行量化评估。
2 基于GPM 数据的昌吉地区降水量空间分布特征分析
2.1 昌吉地区原GPM 数据空间统计特征
研究区原GPM 年降水量栅格面见图1,其共存在2498 个像素,可知其原GPM 像素值介于降水量介于78 mm~508 mm之间,其空间平均值为178 mm,离差系数达56%,呈现自动向西减少的分布特征。需指出的是,该粗糙的栅格像素存在明显机械性特征,无法精细表达降水量空间细节变化。

图1 昌吉地区原GPM 降水量空间分布
利用半方差函数(GS+9.0 软件)检测原GPM 降水数据(图3)栅格像素点之间空间自相关性。由图2 可知,随着空间距离增加,半方差值先从0 值迅速升高,当空间距离达到300 km 距离时,半方差值趋于稳定。统计的其块基比为6.29%,说明存在显著空间自相关,其自相关距离约为30 km,降水量在此范围内呈现互相影响,而超出该范围则相关性消失。上述研究表明,利用RF算法对区域降水量进行空间拟合具有可行性。

图2 研究区降水量半方差函数特征

图3 昌吉地区原GPM 降水量与地面观测值之间一致性
为客观评估研究区GPM 降水量数据可替代性,利用研究区16 个气象站点空间数据提取了对应位置上GPM 像素,并比较二者之间差值。如图3 所示,卫星记录降水量值与地面观测值之间具有较好一致性,散点聚集于1∶1 两侧,仅有少部分离散点;统计得到二者间的R2达0.45,MAE 和RMSE分别为48.89 mm、61.47 mm。由此可知,昌吉地区2020 年GPM 卫星数据在该地区具有一定可替代性。
2.2 基于随机森林的GPM 数据降尺度模型构建
为确保降尺度模型稳健性,利用全部16 个气象站点降水量资料进行充分训练,以地面雨量站观测降水量为目标特征,以DEM、地理经度、纬度和经纬度乘积为协变量,进而训练随机森林回归模型。利用网格搜索算法对该关键参数优化,其中对Importance Coefficient 设定搜索范围为0~1,步长为0.1;mtry 取 值 0~1 之 间 整 数;Regularization value 为0~1 之 间,步长为0.1。由模型参数优化过程可见当mtry、Importance Coefficient 和Regularization value 参数组合配置依次为10、0、0.2 时,此时模型训练精度RMSE 达到最小,仅为14.23 mm。
2.3 基于随机森林降尺度后GPM 降水量空间分布
利用训练好的随机森林回归模型进行降尺度处理得到昌吉州1 km 分辨率水平的降水量空间信息(图4)。可见,降水量值域范围为77 mm~512 mm,其空间平均值为190 mm,这些统计特征与原GPM 数据(图1)相接近。西部南部天山北坡地区降水量较高,可达300 mm 以上,而东部、东北部平原地区较少,仅为200 mm 一下,该分布特征主要受到地形抬升影响。然而,与原始GPM 资料相比,降尺度后的GPM 数据不仅继承了其数值水平和空间分异规律,还突出了在刻画降水量分布细节信息方面的优势,更符合研究区实际。

图4 昌吉地区GPM 数据降尺度降水量分布
2.4 随机森林降尺度模型精度分析
在获取研究区GPM 数据降尺度后栅格面基础上,利用ArcGIS 工具extract 功能提取昌吉州全部气象站点位置上对应的降尺度后降水量数值信息,在此基础以地面观测降水量值为参考,计算二者之间差值。图5 中显示,地面降水量与降尺度后GPM 值之间拟合度较好,二者间的R2达0.703,MAE、RMSE 分别为37.31 mm、42.34 mm,且离散点相对较少。相比于原始GPM 数据,降尺度的GPM 降水量与地面观测值之间的R2提升了62%,而MAE 和RMSE 依次降低了24%、31%。该结果表明,研究区粗糙集GPM 数据经随机森林降尺度处理,提升了数值准确性。
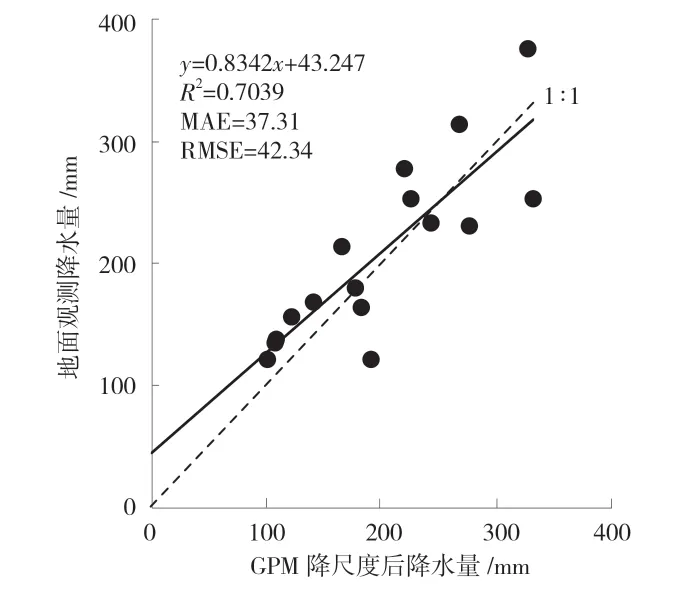
图5 降尺度后GPM 降水量与地面观测值之间一致性
2.5 降尺度后GPM 数据误差分析
为进一步了解随机森林降尺度后GPM 数据具体误差分布,先利用站点数据统计了点基尺度相对误差,再利用Voroni 图进行可视化,具体分析过程为:ArcGIS Geostatistical Analysis →Explore data Voronoi map。如图6 所示,降尺度后GPM 数据误差存在区域性差异,其中对中北部地区降水量存在高估,相对误差约为0~60 mm,对南部山地存在低估,误差约为-78 mm~0 mm。
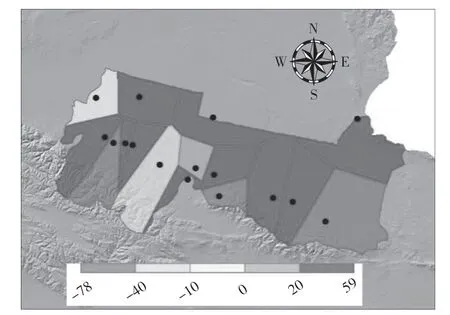
图6 昌吉地区GPM 降水量空间残差分布
3 结论
本研究基于随机森林回归降尺度算法对粗糙集的原GPM卫星降水数据进行尺度变换处理,对昌吉州降水量空间分布进行研究。结果表明,随机森林回归模型通过拟合地面观测降水量与地形、经纬度之间非线性关系,较好模拟了昌吉地区降水量空间细节分布,并展示了空间平滑性和可靠性;经降尺度处理后的GPM 数据精度取得较大提升,生成的降水量空间栅格图显示,区域降水量呈现自东向西、自南向北减少分布规律;区域GPM 数据降尺度后误差呈现由南向北增加分布,南部山区存在低估,北方盆地存在高估。未来研究仍需进一步拓展其他机器学习或深度学习算法在降尺度过程中的应用性,并比较不同非线性回归技术对GPM 数据降尺度的差异性。

